汽车木陶瓷制动衬片热弹性耦合分析

杜丹丰，王麒麟，郭秀荣

(1.东北林业大学 交通学院， 哈尔滨 150040； 2.东北林业大学 机电工程学院， 哈尔滨 150040)

0 引言

目前汽车盘式制动器的制动衬片主要采用金属/半金属钢纤维制动衬片，其容易划伤制动盘且制动噪音大。紫铜/黄铜陶瓷制动衬片摩擦性能优异，但制造成本过高只在少数车型上得到应用[1]。陶瓷制动衬片应用于保时捷轿车中，美国橡树岭国家实验室与Honeywell Advanced composites 公司、Honeywell Aircraft Loading Systems 公司、Honeywell Commercial Vehicle systems 公司合作，正在研制低成本的C/SiC 陶瓷复合材料制动衬片，替代用于载重汽车的铸铁和铸钢制动衬片[2-4]。木质陶瓷是一种在真空炉中对木材或浸渍有热固性树脂的木质材料进行炭化而得到的新型多孔炭材料[5]。具有耐磨损，耐高温，导热能力强、对环境污染小等优势[6]。国内外对木陶瓷的制备工艺[7-9]、理化特性[10-11]、微观结构[12-14]、摩擦磨损特性[15-16]等方面进行了大量研究。木陶瓷材料目前已经作为防弹材料、电池极板材料、电磁屏蔽材料得到了广泛应用[17]。

本文首次提出一种以木陶瓷为摩擦材料的汽车制动衬片。为研究以木材陶瓷汽车制动衬片实用性，基于ABAQUS有限元软件建立了盘式制动器制动过程的热弹性耦合分析模型，在不同工况下分析了应用木陶瓷制动衬片对制动盘温度场及应力场的影响。同时，基于Archard磨损模型，利用UMESHMOTION子程序实现了对制动过程中木陶瓷制动衬片磨损深度的数值模拟。

1 温度-应力-磨损耦合模型

汽车实际制动过程涉及极其复杂的摩擦及热力学现象，为方便仿真模型的建立，在不影响仿真结果准确的前提下，假设制动器各元件的材料组成均匀，均为各向同性材料，且认为制动过程中车轮处于纯滚动状态。

1.1 制动过程的摩擦热

制动器制动过程是一个将车辆行驶时的动能转化为热能的过程，假设汽车制动消耗的动能全部转化为摩擦副产生的热量，制动盘与制动衬片之间相互摩擦表面的热流密度q0满足[18]：

(1)

式中：z代表制动器的制动效能，数值上是车辆的减速度a和重力加速度g的比值；φ表示制动器制动力分配系数；Ad表示摩擦副实际接触面积(m2)；v表示车辆制动初速度(m/s)；εp表示制动盘表面载荷的分布系数；m为整车质量(kg)。

1.2 热弹性耦合模型

对汽车制动器的热弹性耦合过程而言，采用瞬态热分析方法有利于了解摩擦副温度及热应力的变化特点。基于傅里叶方程及能量守恒定律，在笛卡尔坐标系下，瞬态热分析中温度场的控制方程为[19]:

(2)

式中:T表示温度(℃)；ρ为材料密度(kg/m3)；cT为某一温度下材料的比热，J/(kg·K)；kx、ky、kz表示材料沿着坐标轴方向的热传导系数，本次研究中认为材料为各向同性材料；qv内热源强度(W/kg)，其来自摩擦副产生的摩擦热。

根据圣维南原理，将六面体单元的正应变简化为热应变及机械载荷产生应变的叠加。依据线弹性本构关系六面体单元的正应变方程如下[19]：

(3)

式中：εxx、εyy、εzz代表D六面体单元沿坐标轴方向的正应变；E为材料弹性模量；σxx、σyy、σzz为六面体单元沿坐标轴方向的应力；μ为材料泊松比；α为材料热膨胀系数；ΔT为物体温度分布。根据方程可以得到单元沿坐标轴方向的应力。

1.3 制动片磨损数值模型

摩擦过程的磨损深度由摩擦对偶件材料属性、接触压力、滑移速度等多方面因素决定，结合对试验结果的分析产生了许多种磨损量数值模拟方法，本文中选用应用较为广泛的Archard模型[20]。

其磨损模型的基本公式为：

(4)

式中：V为物体磨损体积(mm3)；s为磨损方向位移(mm)；ks为无量纲的磨损系数；FN为黏着节点支撑载荷(N)；σs为材料的屈服极限(N/mm2)。

将方程对时间域离散化为微分模式，时间增量为dt，设接触面积为ΔA，时间增量内磨损深度为dh，则式(4)可改写为：

(5)

设单位接触面积ΔA，在支撑载荷FN作用下接触应力为pc，磨损深度Δh可以表示为：

(6)

在考虑热效应的情况下，由于温度变化引起材料膨胀不均匀，会使接触应力pc产生变化，通过将时间域离散为极小的步长Δt，可以认为瞬时接触应力pc为常数，通过多次迭代最终计算得到磨损深度Δh。

2 热-应力-磨损耦合有限元模型

2.1 盘式制动器三维模型

建立通风盘式制动器三维模型。模型几何尺寸如表1所示。

表1 盘式制动器模型几何尺寸

对盘式制动器制动过程的分析主要关注制动盘与制动衬片之间的热弹性变化及制动衬片的磨损情况，因此在不影响结果准确性的情况下对模型进行了简化。简化后的模型如图1所示。

图1 通风盘式制动器三维模型

2.2 确定摩擦副材料参数

制动盘的材料参数选用HT250灰口铸铁的热物理参数，金属型制动衬片及木陶瓷材料热物理参数通过查阅文献获得[21-23],制动器摩擦副材料参数如表2所示。

表2 制动器摩擦对偶件材料参数

2.3 制动工况确定

假设汽车在不同行驶初速度下以10 m/s2的减速度紧急制动，所选车型车轮半径为0.286 m，计算得到制动时间及制动距离如表3所示。制动压力保持在4 MPa。

表3 紧急制动初始条件

2.4 网格划分及边界条件的确定

根据拓扑结构将制动盘与制动衬片划分为六面体结构化网格，对接触区域进行网格细化，提高计算精度。制动盘和制动衬片均采用缩减积分温度-位移耦合单元C3D8RT，制动衬片网格节点数3 641，单元数2 838。制动器整体划分为21 478个节点，13 856个单元。盘式制动器网格划分结果如图2所示。

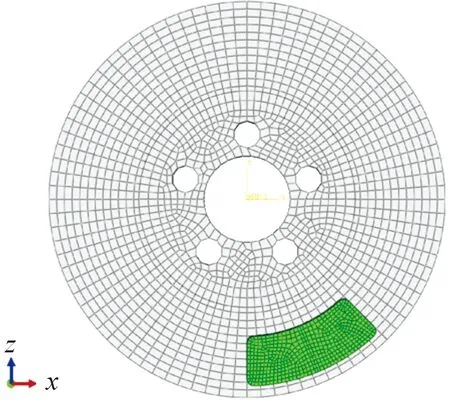
图2 盘式制动器网格划分图

采用主从面对应法定义制动盘与摩擦面之间的接触，将划分网格较大的制动盘表面定义为主面有利于计算结果收敛。文献[23]表明木陶瓷材料的干摩擦因数为0.35～0.39与金属型制动衬片相近，为主要研究木陶瓷材料热物理特性对制动过程的影响，在本次分析中统一选择传统金属型制动衬片的摩擦因数导入到有限元模型中，具体数值如表4所示[24]。

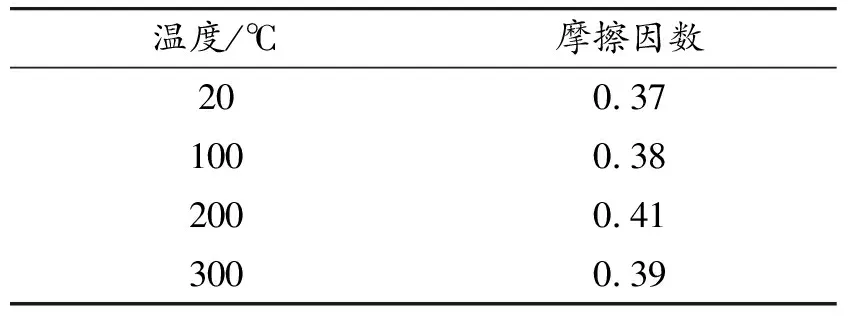
表4 金属型制动衬片与铸钢制动盘之间摩擦因数

热力耦合过程求解采用温度-位移耦合分析步。制动衬片两侧施加4 MPa的恒定压力载荷，只保留制动衬片片上表面的压力方向自由度，制动盘螺栓连接处与轮轴相连，因此限制螺栓连接表面法向自由度。制动盘内圈节点施加转速，转速随时间下降至0。对流换热系数受空气粘度、汽车行驶速度、制动盘转速等多方面因素影响，很难获得准确的数据，通过计算对流换热系数的大致曲线并导入到软件中。设置环境温度为20 ℃，同时也将模型初始温度定义为20 ℃。模型的边界条件设置如图3所示。

图3 制动盘载荷设置示意图

2.5 磨损子模型建立及关联

在每一个增量步结束后，UMESHMOTION子程序将从ODB文件中读取出每一个节点的滑移速率CSLIP、接触压力CSTRESS。计算得到磨损深度后，将其转化为节点位移并通过ALE技术进行网格的重绘。制动衬片磨损深度模拟过程如图4所示。

图4 制动衬片磨损深度模拟过程

3 仿真结果及分析

3.1 制动盘热弹性特性分析

以木陶瓷作为制动衬片材料时，在表3所示制动工况完成后汽车制动盘温度分布如图5所示。低车速工况下，制动盘温度上升不大，最高温度只有55.81 ℃，制动时间短，分布集中于摩擦接触部位。车速越高，制动盘温升越高，120 km/h车速制动结束后，温升185.52 ℃，温度分布也更加均匀，呈现由接触部位向两侧扩散的环状分布特点。

图5 紧急制动工况制动盘温度分布

以木陶瓷制动衬片对应制动盘最高温度节点作为特征点，绘制出不同初速度下节点温度变化曲线如图6所示。

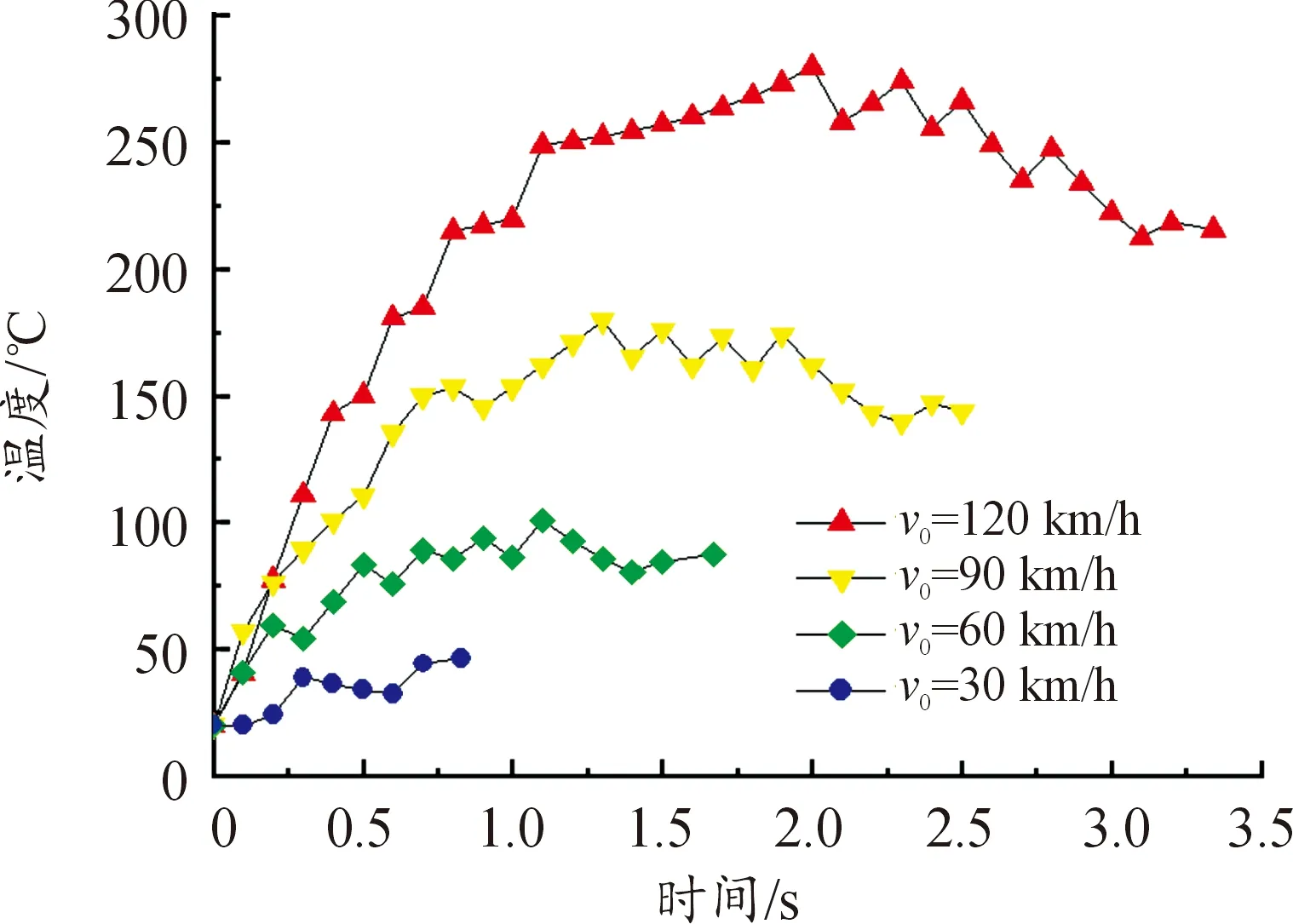
图6 紧急制动工况制动盘温度变化曲线

制动初期，制动盘转速高，摩擦副之间热流密度大，制动盘温度快速升高。随着制动盘转速降低，生热速率下降，温升速率趋于平缓直至生热速率与热传导速率持平，温度达到峰值，在120 km/h初速度下，木陶瓷制动衬片对应制动盘温度峰值达到254.25 ℃，传统金属型制动衬片对应制动盘温度峰值为264.16 ℃。采用木陶瓷制动衬片时制动盘温度变化规律与传统制动器制动盘相似，由于木陶瓷材料良好的导热能力，可以将制动盘温度峰值降低9.91 ℃。

应用木陶瓷制动衬片时，不同初速度工况下，制动盘应力分布特点如图7所示。

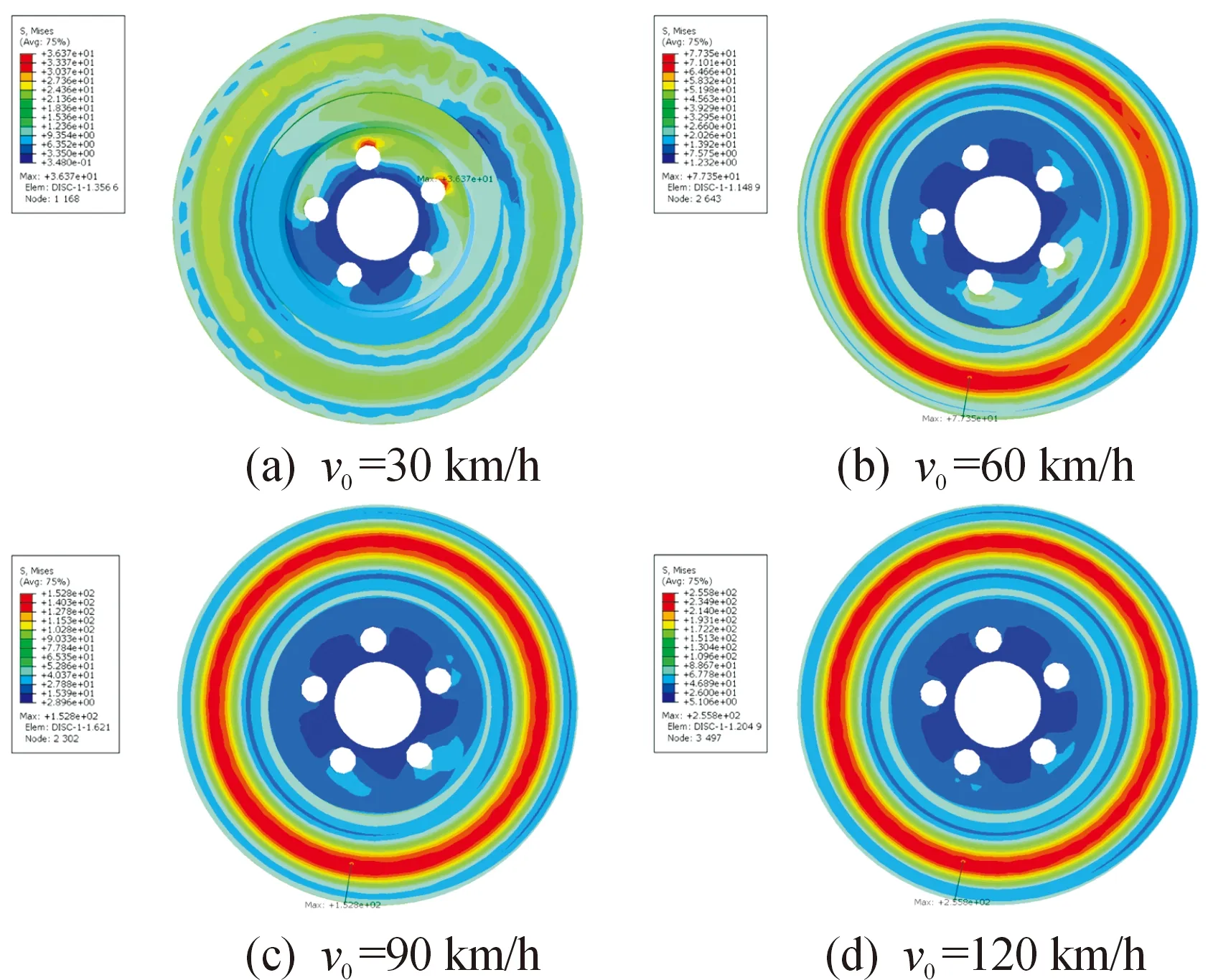
图7 紧急制动工况制动盘应力分布

制动盘与轮轴连接一侧应力远高于盘式制动器外侧，高速车辆制动停止后，制动盘最大应力为255.82 MPa。

3.2 木陶瓷制动衬片热弹性分析

为研究木陶瓷材料热物理特性对制动衬片性能的影响，选取初速度为120 km/h及30 km/h 2种制动工况下，比较木陶瓷制动衬片与金属型制动衬片的温度场及应力场分布。在一次紧急制动结束后，2种制动衬片表面温度分布特点如图8所示，正应力分布特点如图9所示。

图8 紧急制动工况制动衬片温度分布

图9 紧急制动工况制动衬片应力分布

在低速工况下，相较于金属型制动衬片篇木陶瓷制动衬片表面最高温度降低1.41 ℃，高速工况下，表面最高温度降低2.17 ℃。木陶瓷材料热传导能力强，高速工况下可以明显发现，木陶瓷制动衬片温度分布更加均匀。正应力分布状态与金属型制动衬片类似，高速工况下最大应力可达7.35 MPa。选取4种工况下木陶瓷制动衬片温度最大值对应节点，绘制节点温度变化曲线如图10所示。

图10 木陶瓷制动衬片温度变化曲线

由于制动衬片节点始终处于摩擦接触区域，相较于制动盘温度变化，制动衬片温度平稳增长无浮动现象，120 km/h初速度条件下，表面温度最高可达281.41 ℃，远低于木陶瓷材料热解温度，因此使用木陶瓷材料作为汽车摩擦材料具有良好的安全性。

3.3 木陶瓷制动衬片磨损深度模拟

汽车制动过程中，制动衬片会产生变形，从而影响摩擦副之间的接触状态。变形量是由机械载荷的挤压变形，及材料的受热膨胀引起的，同时还包括制动衬片摩擦过程中的磨损现象。木陶瓷制动衬片紧急制动工况下沿Y轴方向的变形量如图11所示。

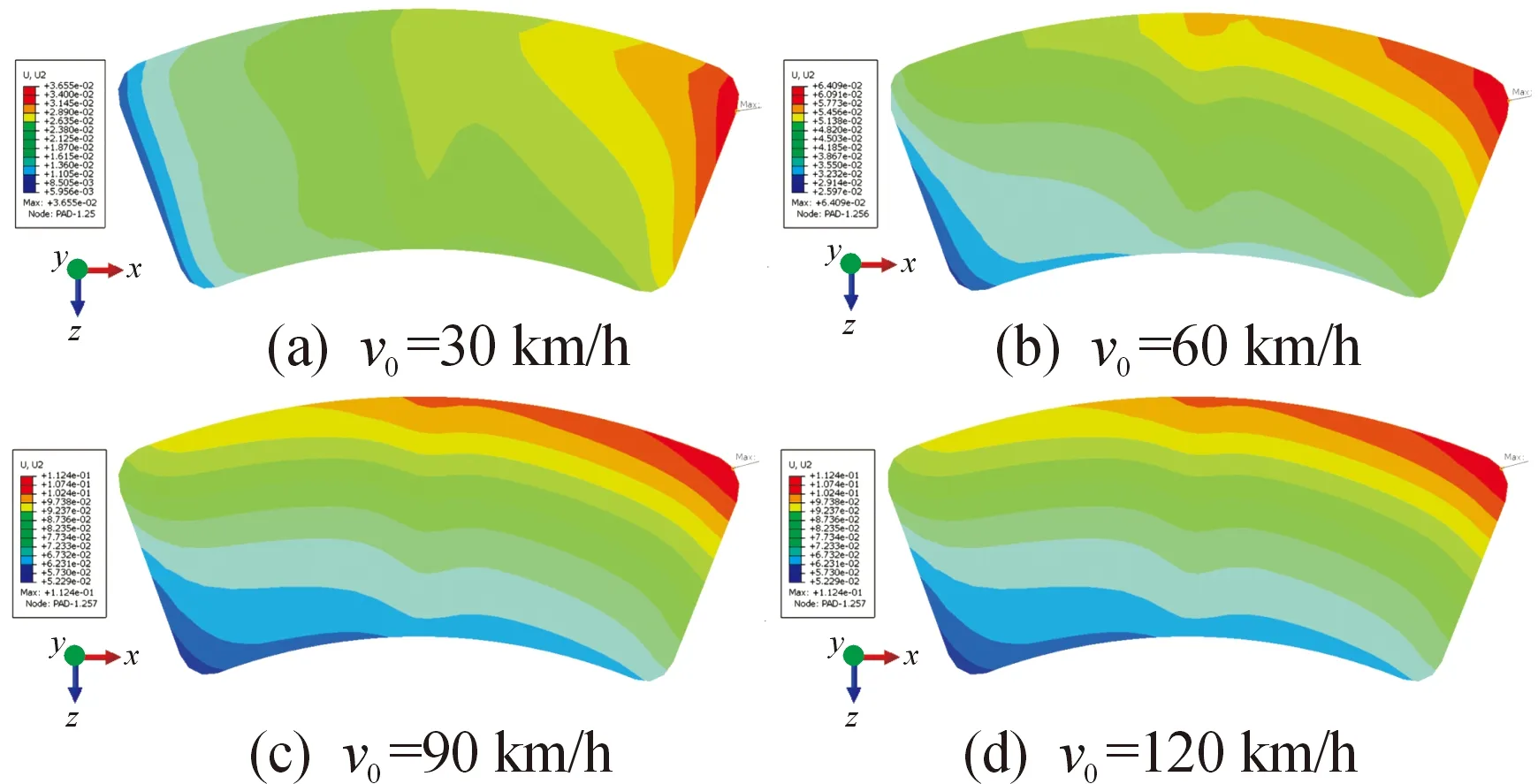
图11 紧急制动工况制动衬片Y轴方向变形量

制动衬片变形主要集中于制动衬片与制动盘之间摩擦基础区域的入口附近，随着车轮转速提高，沿车轮转动方向扩散。在初速度为120 km/h工况下，变形量最高可达112.42 μm。与变形量类似，在摩擦接触边缘，制动衬片实际磨损也更为严重。故选取制动衬片变形量最大节点，通过子程序导出该节点磨损深度曲线如图12所示。

图12 制动衬片磨损深度曲线

车轮转速越快，制动时间越长，制动衬片磨损越严重。一次高速紧急制动过后，木陶瓷制动衬片节点磨损深度最大可达2.11 μm。

4 木陶瓷制动衬片结构优化

由于木陶瓷制动衬片在耐磨性方面明显优于传统金属型汽车制动衬片，因此主要以进一步降低制动盘温度最大值为目标，对木陶瓷制动衬片内外径及包角进行优化，通过修改rpy文件得到8组不同结构参数下得到120 km/h初速度工况下的制动盘温度最大值如表5所示。

将8组数据输入Matlab软件并进行线性回归，回归平面如图13所示。以制动盘节点温度最大值为目标，利用线性回归模型对制动衬片的内外径及包角进行参数优化。优化结果如表6所示。

图13 数据回归平面

表6 优化结果

预测制动盘温度误差为1.12 ℃，误差率为0.44%，可以认为预测模型基本可靠。

将优化后结构尺寸后的模型重新提交计算，得到的制动盘节点温度变化如图14所示。节点温度峰值下降1.79 ℃。

图14 优化效果曲线

5 结论

本文建立通风型盘式制动器热-应力-磨损耦合模型，采用木陶瓷材料作为汽车制动衬片摩擦材料与传统金属型制动衬片进行对比，分析了木陶瓷制动衬片对盘式制动器温度及应力分布的影响。基于UMESHMOTION子程序及ABAQUS软件的ALE网格自适应技术，实现了对木陶瓷制动衬片磨损情况的数值模拟，得出了以下结论：

1) 以木陶瓷作为制动衬片摩擦材料，车辆在120 km/h车速状态下制动后，制动盘节点最高温度为200.82 ℃，相较于传统制动器制动盘温度下降9.91 ℃。能有效缓解因制动盘“热衰退”现象造成的摩擦副有效摩擦因数下降，缩短汽车制动距离，提高车辆安全性。

2) 高速紧急制动状态下，木陶瓷制动衬片制动过程中温度最高可达281.41 ℃，远低于木陶瓷热分解温度，以木陶瓷制动衬片制动效能稳定性更强。

3) 以木陶瓷作为制动衬片摩擦材料，单次高速紧急制动磨损深度最大不超过2.11 μm，具有良好的耐磨性。

4) 通过Matlab线性拟合方法，以制动盘温度峰值为目标，进行了木陶瓷制动衬片结构尺寸的优化，优化模型误差率为0.44%，优化后制动盘温度峰值降低1.79 ℃。