锂电池容量衰退模型数据驱动方法研究

臧帏宏,李中华，王发成,周 伟

(1.中国北方车辆研究所， 北京 100072； 2.陆军北京军代局， 北京 100050)

0 引言

随着石油能源逐渐枯竭和环境污染日益严重，以纯电动汽车为代表新能源车辆成为当下车辆的行业的焦点。锂离子动力电池系统作为新能源车辆的核心部件，有效的电池管理系统可以提高整车性能并增加使用安全性[1]。其中，锂电池的剩余容量预测是热点研究课题。

目前，能够表征电池性能退化最直接的参数为电池的剩余容量[2]。然而在实际工作状态下，剩余容量难以通过直接测试途径获得。需采用易于测量的电池特征参数对锂电池剩余容量进行预测[3-4]。Liu等[5]根据电池放电过程中的电压电流曲线，提取等压降放电时间序列作为特征输入，采用相关向量机来对锂电池进行剩余容量预测。电池在车辆实际运行的条件下，电池可放出的最大容量随着运行时间逐渐衰减[6]。可对电池无负载时的开路电压进行特征提取[7-8]。

电池剩余容量预测主要分为集总参数法、数据驱动法和融合法。集总参数模型包括电化学模型、等效电路模型等，前者需要通过复杂仪器对锂电池容量衰减过程中的电化学特征进行采集和分析，可建立高精度单体模型，模型也可体现实际物理、化学意义，但这种方法多用于对电池单体微观特性的分析与研究领域，建模工作量大，且动态性能较差；后者通过对等效电路模型中的欧姆内阻、极化内阻和极化电容进行离线或者在线的参数辨识，作为表征电池老化程度的健康因子,但其参数辨识结果受模型精度、辨识方法和运行工况等诸多因素的影响。

基于数据驱动的预测方法主要通过对电池运行过程中收集到的状态信息进行统计分析，找到与电池容量衰退紧密相关的特征值作为健康因子(health index,HI)，预测方法包括自回归(autoregressive,AR)模型[9]、人工神经网络(artificial neural network,ANN)[10-11]、高斯过程回归(gaussian process regression,GPR)[12]、支持向量机(support vector machine,SVM)[13]、相关向量机(relevance vector machine,RVM)[14]等。洪元涛[15]采用极限学习机算法对循环寿命测试方法进行优化。赵沁峰等[16]使用灰狼算法优化的极限学习机算法对电池剩余寿命实现间接预测。陈则王等[17]采用遗传优化算法对锂电池在极限学习机上的应用进行初始参数优化，均得到了较高的预测精度。李练兵等[18]提出了容量增量分析法提取IC曲线拐点值，并利用神经网络中的Elman算法构建剩余容量预测模型，选用的数据为NASA提供的公开数据集。但其依据的模型公式建立在放电电流充分小可忽视电池内阻压降的前提条件下[19]，公开数据集中的充放电的电流大小明显并不符合差分电压公式成立条件。

综上，众多学者在动态充放电曲线中提取特征值，但是易受电池运行工况影响。为了避免负载影响，本文提出以放电结束后电池电压压升参数作为表征锂电池内阻变化、容量衰退的健康因子，并利用选用误差向后传播(back propagation,BP)算法及SVM两种算法对电池进行剩余容量预测。

1 BP和SVM模型

1.1 BP模型

BP是一种基于误差反向传播方法训练的前反馈型算法，输入的变量进行前向传播，经过隐含层迭代计算，通过输出层输出结果。在算法模型训练过程中，根据设置的训练步长、迭代次数限制和误差阈值，输出误差从输出层反向传播给中间隐含层及输入层，从而使得各层连接权值自动修正，其拓扑结构如图1所示。

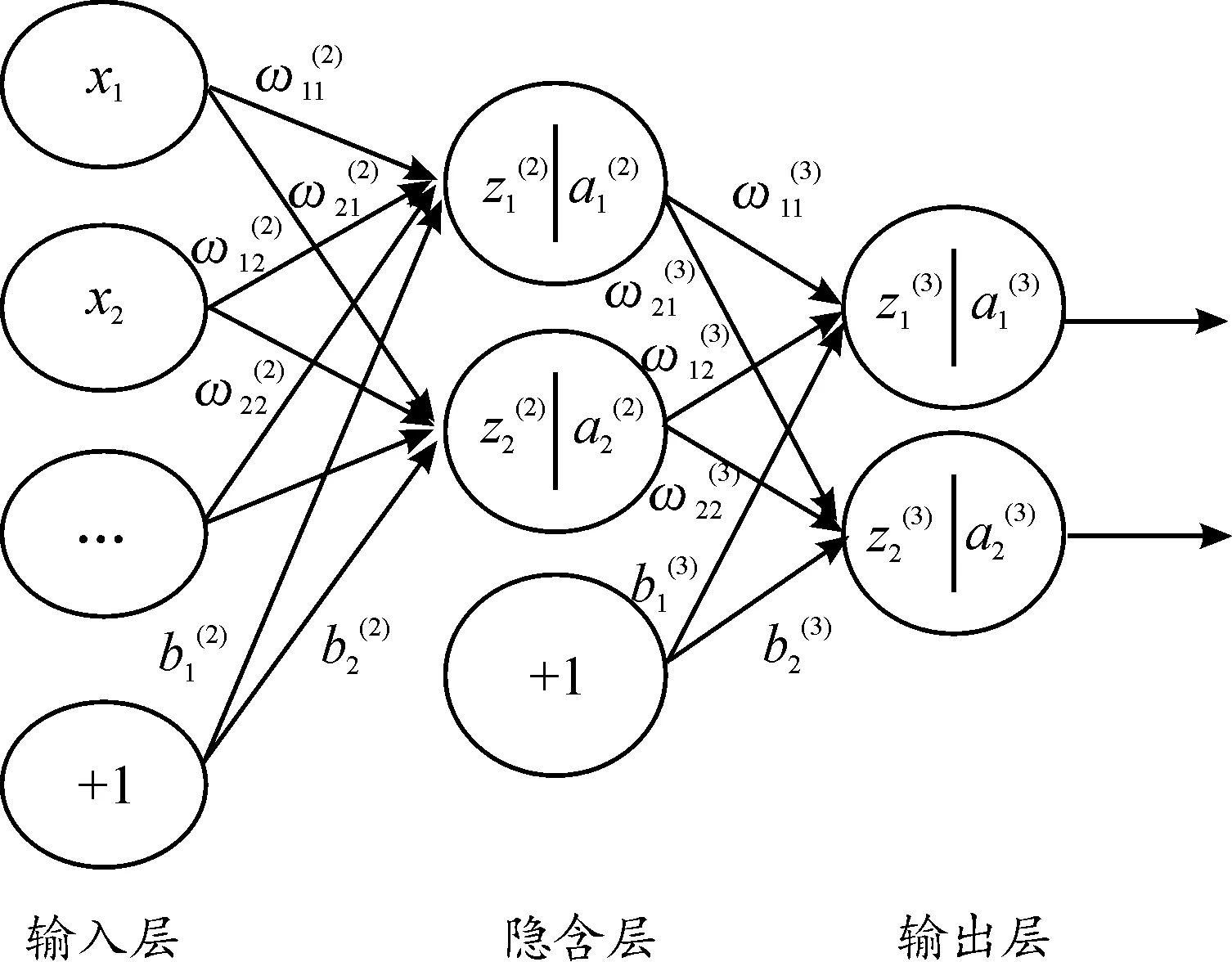
图1 BP拓扑结构示意图

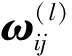
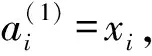
第2层神经元的状态和激活值可由式(1) (2)得出

(1)

(2)

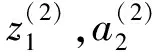
第3层神经元的状态和激活值可由式(3)(4)得出

(3)

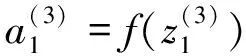
(4)

故第l层神经元的状态及激活值为

z(l)=W(l)a(l-1)+b(l)

(5)

(6)

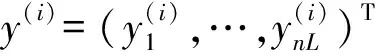
(7)

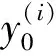
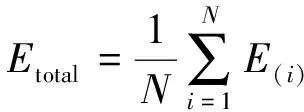
(8)

通过调整权重和偏置使式(8)最小，并确定出此时的W(l)和b(l)，代回式(5)(6)得到输出值。

1.2 SVM模型

Vapnilk等在SVM分类的基础上引入了不敏感损失函数ε，从而得到了回归型支持向量机(support vector machine for regression,SVR)，对小样本数据具有较好的学习泛化性能。在应用于回归拟合分析时，基本思想不再是寻找一个最优分类面使得两类样本分开，而是寻找一个最优分类面使得所有训练样本离该最优分类面的误差最小，对于一般线性回归的SVM数学原理如图2所示。原理为其在线性函数两侧制造了一个“间隔带”，间距为ε，对所有落入到间隔带内的样本不计算损失，也就是只有支持向量才会对其函数模型产生影响，最后通过最小化总损失和最大化间隔来得出优化后的模型。

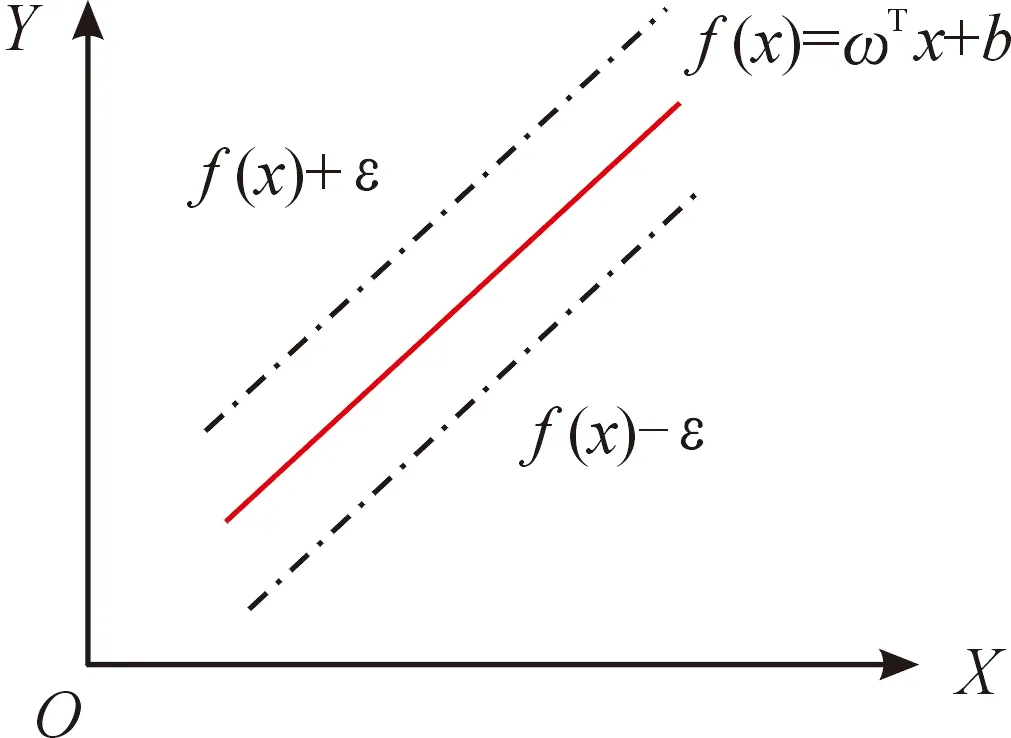
图2 SVM数学原理示意图

假设训练集数据为(xi,yi;i=1,…,n)，xi∈Rn,y∈{-1,1}，其目标是找到一个最优函数即式(9)使得f(x)与任意训练数据的最大偏差小于用户定义的不敏感损失系数ε，同时保持最高的平整度。

f(x)=〈ω,x〉+b

(9)

其中,ω表示参数向量，〈·,·〉表示点积。超平面必须满足式(10)的约束

yi-〈ω,x〉-b≤ε+ξi

(10)

式中：ε表示不敏感损失系数，在实际应用中，由于很难直接确定合适的ε来保证大部分数据都在间隔区间里，所以加入松弛变量ξi，从而降低函数的间隔要求，可以允许一些数据点不在间隔区间里。最优回归超平面的定义如下：

(11)

在式(10)的约束下。选取一个合适的C值。使用拉格朗日乘子法求解优化问题，其中最优值是拉格朗日乘子的鞍点值，α和β是拉格朗日乘数。

(12)

生成的优化目标函数具有以下形式，其中xi是支持向量：

(13)

而实际应用中，回归问题往往为非线性问题，但不需要显式地指定非线性变换，采用核函数来替换线性问题当中的内积，选取适当的核函数K(x,g)和C值。常用核函数中径向基函数是较优的选择。文献[20]对基于不同核函数的SVM算法进行了分析和仿真比较，得出SVM在回归应用中，基于径向基函数SVM的性能要优于基于其他核函数的SVM，表达式如式(14)所示。

(14)

式中：g为核函数参数，文章采用网格交叉验证的方法确定合适的C值和g，进而确定最优SVR函数。

2 数据集分析

选用市面上某款42 Ah三元锂电池单体在室温条件下进行充放电及静态搁置的寿命循环测试数据为样本数据。电池单体测试设备为用于动力电池充放电的Arbin BT2000测试仪、用于温度控制的温箱、用于人机交互和数据存储的上位机。Arbin BT2000测试仪每个工作通道允许的工作电压范围为0～5 V，能够以±100 A的电流对电池进行充放电。单体测试仪、温箱和上位机均可同时记录动力电池的电流、电压、温度、充放电容量等数据。电池单体信息见表1。试验依据按照GB/T 31484—2015《电动汽车用动力蓄电池循环寿命要求及试验方法》。

表1 电池单体信息

试验步骤如下：

1) 恒流充电：1 C(42 A)充电，直至单体达到上限4.2 V；

2) 恒压充电：保持电压在4.2 V，直到充电电流降至0.05 C(2.1 A)，结束充电；

3) 充电搁置30 min；

4) 恒流放电：1 C(42 A)放电，设定单体电池的放电终止条件为2.8 V；

5) 放电搁置30 min。

按照步骤(1)至(5)连续循环511次，记录每次循环的电压、电流及放出的容量数据。其剩余容量随循环次数的变化曲线如图3，该三元电池在循环测试过程中，容量衰减基本呈现线性规律，存在较少容量增生情况。511次循环之后，可放出的最大容量为39.673 Ah，与初始测得的放出容量44.077 Ah相比，衰减了9%，电池循环寿命性能较好。

图3 电池剩余容量随循环次数衰减曲线

3 电池健康因子确定

如图4不同循环次数充电过程中电压随时间变化曲线，电压首先迅速升高至3.8 V左右，然后斜率减缓，在电压将要达到上限前斜率稍有变大，最终电压稳定保持在4.2 V下继续小电流充电。在电池充电截止电压恒定的情况下，随着循环次数增加，电解液和电极材料发生化学反应消耗锂离子，导致锂离子电池内阻增加、容量衰减，电池越快达到截止充电电压，恒流充电时间逐渐减少，整体充电时间逐渐缩短。

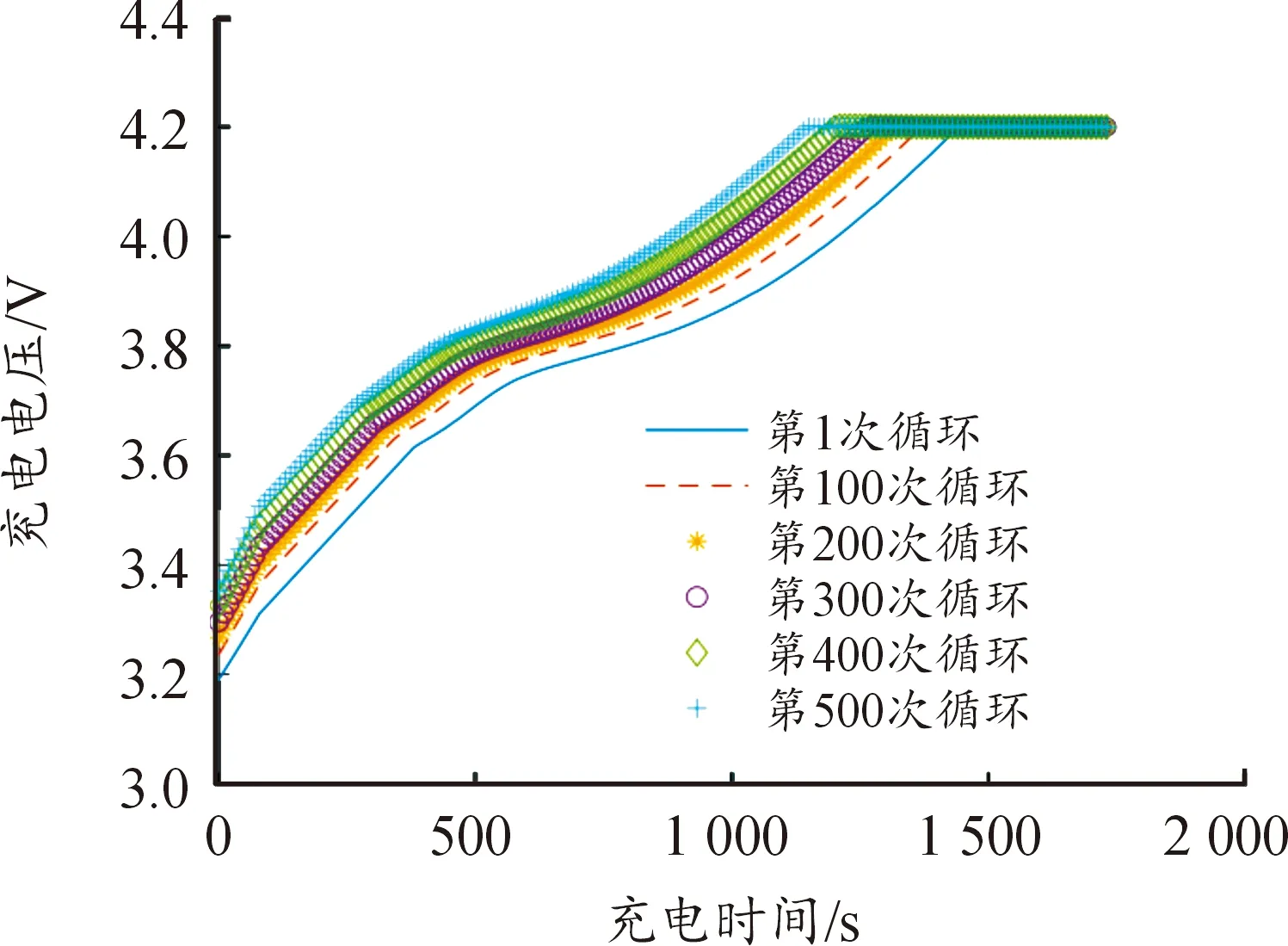
图4 不同循环次数充电过程电压随时间变化曲线

由图4可以看出，随着循环次数的增加，充电起始电压在不断升高，考虑到放电过程均为统一放至2.8 V，且均在放电后搁置30 min，因此可知测试的目标电池在放电结束后搁置相同的时间后，电压回升的程度随循环次数的增加而提高。

图5所示为目前广泛应用的电池等效电路一阶模型，由图5可知，电池内阻不仅包括欧姆内阻R0，还存在极化内阻R1和极化电容C1，图中RL为负载。随着动力电池在循环过程中逐渐老化，内阻增大，放电时由内阻造成的压降也就越大，因此从1C放电状态进入搁置状态，电流从1C突变成为零，欧姆内阻导致的压降迅速回升，极化内阻造成的压降逐渐回升。另外，在充放电过程中，电池电极附近的离子浓度变化会导致内阻增加，搁置期间，离子浓度逐渐趋于平衡，进一步导致电压发生变化。因此，搁置期间电压回升情况一定程度上可以表征电池内部参数变化的过程，也就可以考虑用来表征电池容量衰退老化的情况。

图5 电池等效电路一阶模型示意图

图6为放电搁置期间电压随时间变化曲线。由图可以看出，随着循环次数增加，放电搁置期间电压升高拐点值越偏后，压升程度也越大，表明该电池老化程度越高。图7为放电搁置后电压随循环次数变化曲线。由图7可以看出,多次放电搁置后的电压序列与老化程度之间存在近似的线性关系，所以选取放电搁置阶段压升序列为健康因子，利用BP和SVM原理对电池剩余容量进行预测。

图6 放电搁置期间电压随时间变化曲线

图7 放电搁置后电压随循环次数变化曲线

4 剩余容量预测分析

4.1 预测过程

采用压升序列前400个数据作为训练样本，后111个数据作为测试样本，构建的BP神经网络为单隐层结构，考虑到容量衰减曲线具有良好的线性特征，故设定隐层节点数为2，训练步长为0.01。网络训练函数选用BP算法中计算速度最快的Levenberg-Marquardt法来优化更新权重和偏差值。

在SVM模型中对训练集和测试集采取交叉验证的方法比较精度，并采用式(15)对预测结果进行评价。

均方误差MSE(Mean Squared Error)是各数据偏离真实值差值的平方和的平均数

(15)

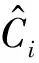
4.2 预测结果分析

分别采用BP和SVM模型，选取搁置阶段压升序列作为健康因子，经过前400次循环数据样本训练，对后续111次循环数据进行电池剩余容量预测。图8所示为BP和SVM模型预测结果。

图8 BP和SVM模型预测结果曲线

由图8可以看出2种模型预测数据与试验数据的趋势变化一致；图9为BP和SVM模型预测误差散点图，由图9可以看出，BP模型预测最大误差为1.40%，而SVM最大预测误差为0.65%。两种模型均能够较好预测，相比BP模型，SVM的可以有更高的精度。

考虑到电池容量的衰减虽然是每时每刻都在发生的，但由历史离线测试数据可知，每次充放电循环后所导致的容量微小的衰退要经过一段时间累积后才会导致电池开路电压的变化，因此不必每时每刻都对电池单体进行剩余容量预测，否则一方面加重BMS算力负担，一方面也会使剩余容量预测时易受到采集精度误差较大的数值的影响，从而导致结果发散。同时，SVM作为一种基于数理统计的机器学习模型被多次验证，针对小样本数据具有良好的鲁棒性，因此本文在与BP神经网络预测的效果进行比较时，推荐使用SVM算法，而非人工神经网络算法。

图9 BP和SVM模型预测误差散点图

5 结论

1) 三元锂电池多次循环放电搁置阶段的压升序列与剩余电池容量存在明显相关关系，把放电阶段的电压升作为健康因子可以对锂电池进行寿命预测。可为同类型三元锂电池实车应用时进行剩余容量分析时的理论参考。

2) BP和SVM模型均可对三元锂电池的剩余容量进行高精度预测，相比BP，SVM有更出色的表现，更适合小样本预测，运行速度更快，在实际应用中，可减小数据采集数量，节省硬件存储空间，更容易实现电池剩余容量在线预测。