“生长数学”理念下的结构化教学
——“反比例函数单元复习课”的教学设计与思考
江苏省太仓市实验中学
赵红琴
《义务教育数学课程标准(2022版)》强调:“在教学中要重视对教学内容的整体分析,帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化数学知识体系.”数学单元复习课就是帮助学生巩固、梳理、整合和提升的过程,帮助学生学会用整体的、联系的、发展的眼光看问题.下面笔者以“反比例函数单元复习课”为例,谈谈基于“生长数学”理念下的结构化教学设计.
1 “生长数学”理念下的教学价值判断
反比例函数是初中数学中的基本函数之一,是中考的必考内容.反比例函数的主要内容包括概念、图象、性质和应用.反比例函数相比已经学过的一次函数有明显的不同:从“式结构”[1]来看,表达式右边一个是整式,一个是分式.从“形结构”[1]来看,一个是连续的直线;一个是曲线,分两支.反比例函数难度明显增加,是对一次函数的提升.从整体来看,反比例函数所处的位置至关重要,与前面的一次函数、方程、不等式、三角形、四边形、分式都有着密不可分的联系,也是今后学习二次函数以及高中函数知识的基础.反比例函数的复习课起承上启下的作用,优化的设计必然起到事半功倍的作用.
从学生角度来看,学生已经具备了坐标系、函数的知识,并类比一次函数的学习经验对反比例函数的概念、图象、性质和应用进行了探究,积累了研究函数的思维活动经验,对建立函数模型和数形结合思想也有了进一步的体会.但是,学生对反比例函图象和性质的理解并不深刻,特别是对于反比例函数增减性的理解经常与一次函数混淆,对于与方程、不等式的综合判断以及与四边形的整合问题都有一定的困难.因此,本节复习课的目标确定为:以数形结合思想为立意,通过读图、识图引导学生进行知识梳理,通过问题串探究构建反比例函数的结构关系,通过拓展延伸完善知识体系.难点是深层次理解反比例函数的图象和性质.
本节课从学生已有经验出发,设计生长途径,经历从点状教学转化为结构化教学的过程,创造具有生长力的数学课堂,激发学生积极主动构建知识体系,在合作交流中提高解决问题的能力,培养学生数学核心素养.
2 教学价值指引下的活动设计
2.1 情境引入,激活结构
问题1如图1,根据图象你能得到什么信息?
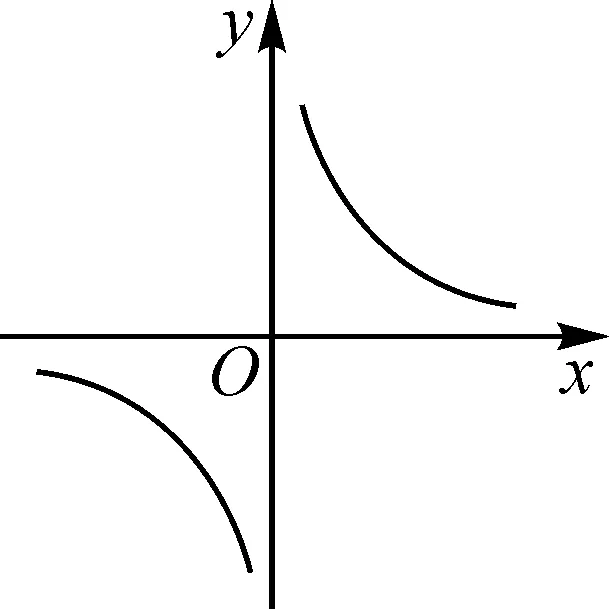
图1
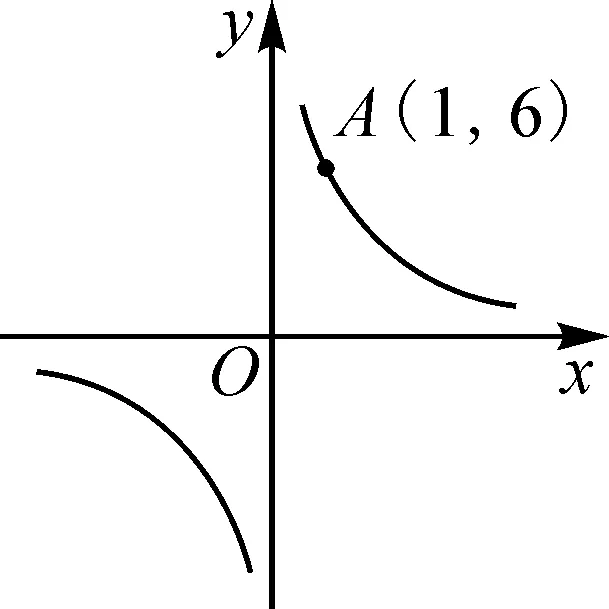
图2
预设生成:结合图形学生可以读出——这是一个反比例函数的图象;图象在一、三象限,k>0;在每个象限内y随x的增大而减小.引导学生举例说明为什么要强调“在每一个象限内”,加深对增减性的理解.反比例函数的图象既是中心对称图形也是轴对称图形,直线y=x和y=-x是其对称轴.
设计意图:通过一个开放式的问题对反比例函数的性质进行复习和归纳,也是对学生已有的知识结构进行复习和梳理.由于起点低,各个层次的学生都有能力参与,通过小组合作、自主表达、相互启发、相互补充,激发学生思维,也为后续的复习做准备.
2.2 结构关联1——不等式与一次函数
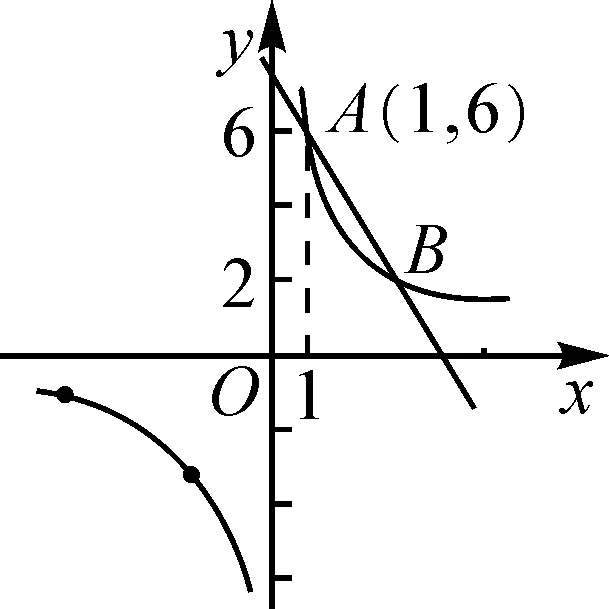
图3
预设生成:学生可以利用不等式进行解答或者结合图象进行直接判断.由此得到x>1时,0
学生能轻松说出B点坐标是(3,2),也能求出直线AB的解析式为y=-2x+8.
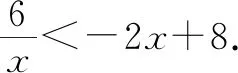
设计意图:问题2一方面可以通过不等式进行解答,另一方面也可以结合图象直接判断.但追问中的问题,如果再解不等式就非常麻烦,而根据图象就非常简单.让学生体会反比例函数与一次函数、方程、不等式之间的联系,深刻体会到用数形结合思想解决不等式问题的优越性,提高学生的阅图能力.
2.3 结构关联2——图形的面积
问题3在上述追问的条件下,连结OA和OB,求△OAB的面积.
预设生成:学生先独立思考,小组交流,然后逐一展示不同的解法.可能会出现以下几种方法,引导学生归纳总结.
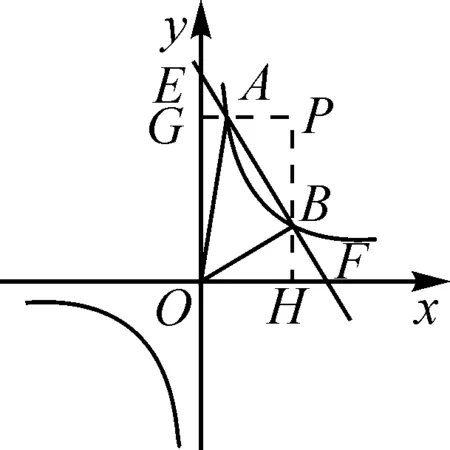
图4
图5
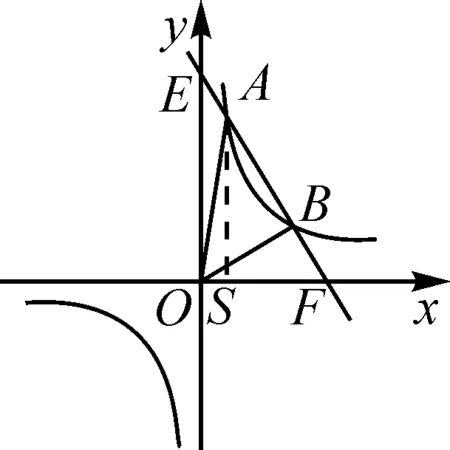
图6
法一:如图4,S△OAB=S△OAF-S△OBF=8或S△OAB=S△OBE-S△OAE=8.法二:如图4,S△OAB=S矩形OHPG-S△OAG-S△OBH-S△APB.法三:如图5,S△OAB=S梯形AMNB+S△OAM-S△OBN.法四:如图6,S△OAB=S△OAS+S△BAS.
设计意图:通过不同的方法,促使学生对坐标系内利用割补法求图形的面积有了进一步认识.引导学生归纳割补法的本质是“化斜为直”,充分利用平行于坐标轴的线段进行割补.从“形”的角度转化为图形的面积的和或差求解,从“数”的角度转化为求点的坐标进而转化为求水平线段或者铅垂线段的长度.割补法的复习和深化为学生今后解决二次函数中的面积问题积累了经验,具有长远意义.
2.4 结构关联3——平行四边形
问题4在上述追问的条件下,如图7,作直线OA,OB,分别交抛物线的另一支于点C,D,试判断四边形ADCB的形状.
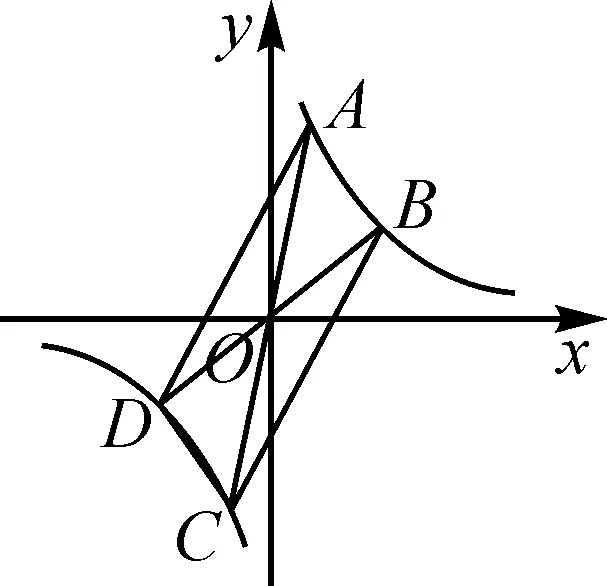
图7

图8
预设生成:由反比例函数的对称性可知,OA=OC,OB=OD,得到四边形ADBC是平行四边形.学生根据平行四边形的性质还可以很快求出四边形ADCB的面积是△OAB面积的4倍.

让学生分组讨论,展示不同的画法,并由学生解释画法的依据.

追问2:若已知A(1,6),B(6,1),如何分别在x轴和y轴上各找一点P,Q,使得P,Q,A,B四点构成的四边形为平行四边形.让学生分析思路,课后解答.
设计意图:“平行四边形”和“反比例函数”的图象都是中心对称图形,问题4及追问让学生充分体会利用对角线互相平分这一性质来判定平行四边形的简洁.追问1让学生动手画矩形并说明依据,这一过程引发学生对矩形判定方法的深度思考,激活了学生储存的知识.“平行四边形”和“反比例函数”两个章节都在苏教版八下教材中,这样的设计将二者有机结合,起到了跨章复习的效果,体现了大单元整体设计的理念,体现了知识的关联性和整体性,有效促进学生整体知识结构的形成.
2.5 结构关联4——图形的运动
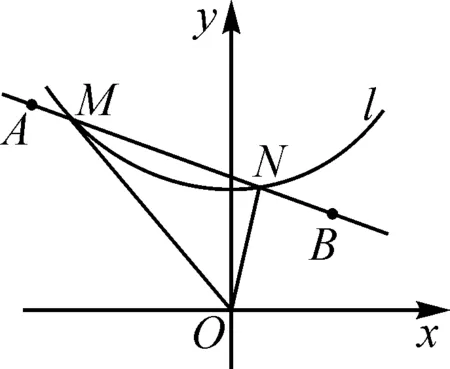
图9

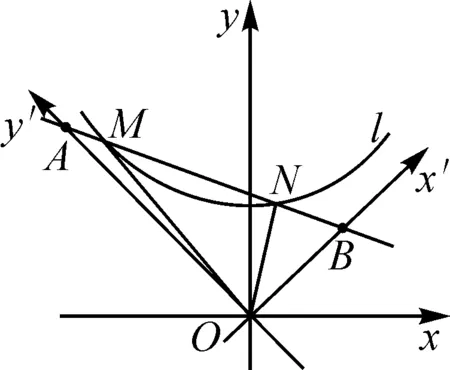
图10
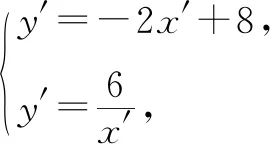
设计意图:图形的运动变换始终贯穿于数学学习中,问题5以一道中考题作为拓展延伸,创设了一个新的情境.反比例函数的图象出现在不同寻常的位置,激发了学生不一样的思维灵感,引发学生联想和思考,让本节课的设计变得更为新颖和灵动,透过场景看本质,方法迁移,难点化解,从而达到问题解决的目的.
2.6 反思悟学,再生结构
教师和学生一起总结本节课的体会,进一步构建知识结构图.
设计意图:通过师生互相补充总结,学生完善已有知识结构,对反比例函数有更深入的了解,同时让思路关联、数学方法得到梳理,能力得到提升.如图11所示.
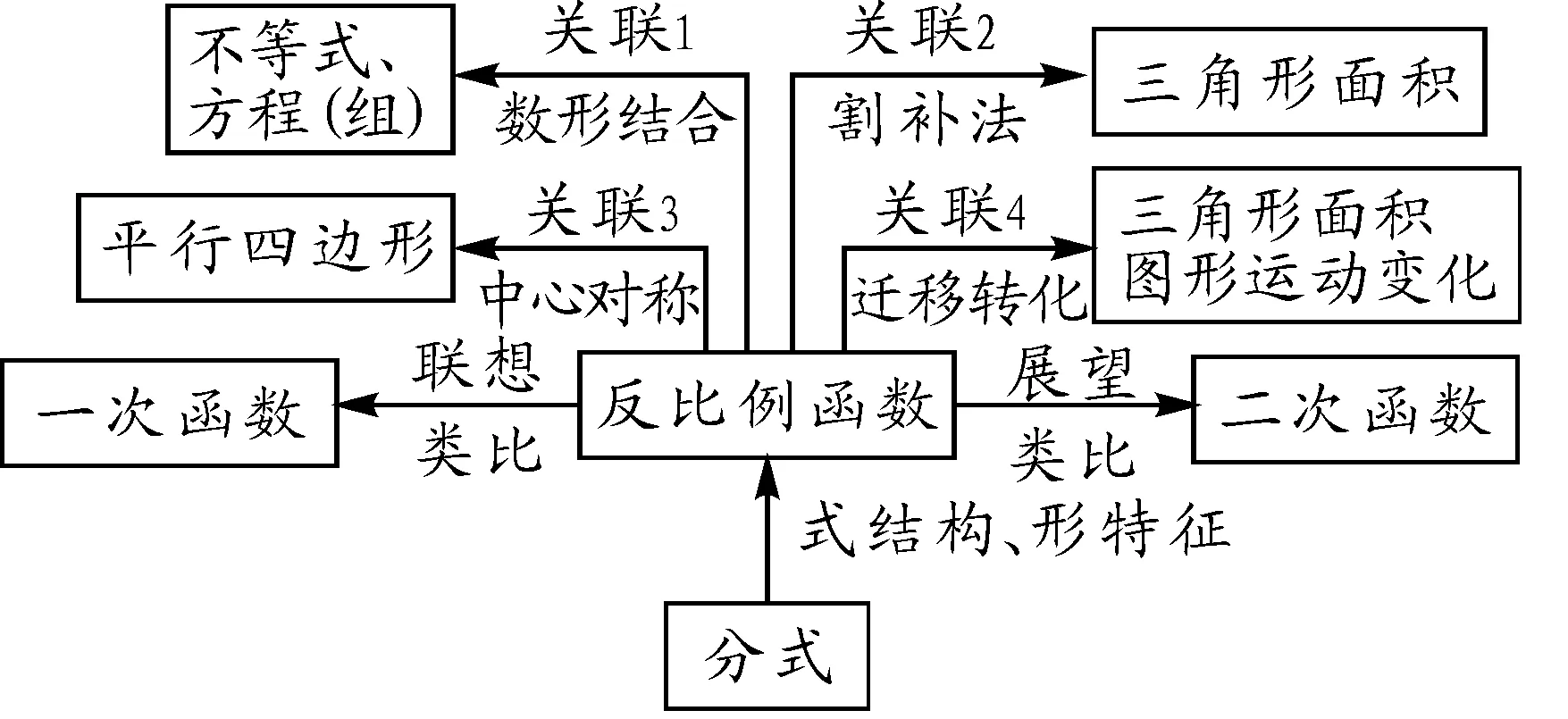
图11
3 活动设计下的教学思考
3.1 一图一课,促进自然生成
本节课以最简单的反比例函数图象为生长点设置了开放性的问题,激活学生已有的知识结构,设置了五个递进式问题作为生长途径,以适时的追问启发学生深层思考,发展学生的思维;指导学生阅图,帮助学生从形的特征、解析式的结构上得到统一理解,有序比较,使相互关系一目了然,进一步促进问题依次深入、层层展开、浑然一体.尊重学生思维的差异性,让问题更具开放性、层次性,激发不同层次学生的参与,让反比例函数的核心知识在问题串的引导下慢慢生长.
3.2 问题关联,彰显结构化教学
结构化的教学设计可以体现知识的整体性、思路的关联性和方法的迁移性[2].本节复习课,不仅把反比例函数离散的知识串联了起来,还通过结构关联把反比例函数和前面已经学过的平行四边形等知识有机整合,达到跨章复习的效果,充分体现了知识的整体性和系统性.课堂上适时的追问和变式激活学生的灵感,很好地促进了深度思考,让学生的思路得到拓展、延伸.归纳和总结环节给学生厘清思路的时机,促使解题方法得到优化和迁移,学生的结构性思维在感悟中逐步形成.
3.3 自主探究,提升数学素养
教学设计的问题起点低,给不同层次学生机会,让学生体验成功的喜悦,激发学生表达的热情,为活动起到很好的铺垫作用.活动过程中采用了一题多解、自主提问、互编互助等形式,给学生创造了小组合作的情境,优化学生学习方式,引导学生深度参与,处处体现了以生为本、让知识与生命共同成长的理念.以数形结合思想为主,渗透了转化、分类讨论等数学思想方法,有效地发展了学生核心素养.

