基于“一题一课”的中考探究式复习课的实践研究*
——以 “二次函数为基架的角度问题”为例
成都七中英才学校
凌 银
《义务教育数学课程标准(2022版)》中提出“会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界,通过学科实践实现其独特育人价值”[1].在课标的引领下,在“双减”的时代背景下,如何将中考复习课上得更有效率、更有趣味,从而更好地帮助学生深入理解知识点,值得深入思考.
探究式教学法由美国实用主义学者杜威提出,在具体教学操作层面可分为五个步骤:创设情境、产生问题、自主探究、得出结论、当堂训练.中考复习课应以发展学生的学科核心素养为导向,创设合适的教学情境,通过问题驱动,启发学生思考,探寻事物的变化规律,引导学生把握数学内容的本质,让“课堂思考”成为提升学生学力的有效途径,让“减负提质”真正地落地生根.笔者以一节“二次函数为基架的角度问题”的中考复习课为例,将本节课主要过程呈现如下,与读者交流.
1 教学过程
1.1 环节一:温故知新
师:同学们,我们在初中阶段学过哪些判定两个角度相等的办法呢?
生1:借助三角形的全等和相似.
生2:借助尺规作图.
生3:度量法.
1.2 环节二:自主探究
在复习回顾的基础上,让学生做如下探究.
问题展示:如图1所示,已知A(-1,0),B(3,0),C(0,-3),D(6,0),试探究∠ACO和∠BCD的数量关系.你能用哪些方法说明?

图1

图2
生1:如图2所示,构造直角三角形,利用三角函数求解.
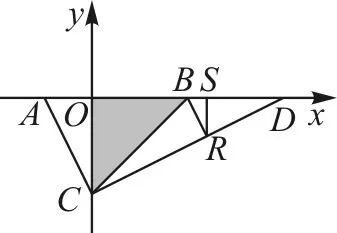
图3
生2:如图3所示,构造一线三垂直模型,即K字模型.
设计意图:从简单问题入手,引导学生思考判定两角相等的常见方法,为后面学生自主探究作铺垫.
1.3 环节三:类比探究

图4
如图4所示,我们引入一条过A(-1,0),B(3,0),C(0,-3)三点的抛物线,你能将刚才的问题与这条抛物线结合起来吗?请结合抛物线设计一个问题并给出解答过程.请同学们小组内进行讨论.
问题1:在直线BC下方抛物线上寻找一点P,使得∠ACO=∠BCP.
问题2:在抛物线上寻找一点P,使得∠ACO+∠BCP=90°.
问题3:在抛物线上寻找一点P,使得∠BCP=2∠ACO.
师:我们先来解决问题1.


图5

图6
师:若取消“在直线BC的下方”这个条件,那么还有其他情况吗?
生2:如图6所示,将点E关于直线CB对称得M(2,1),同理可以求出直线CM的解析式,联立二次函数解析式求解P2.
生3:如图7所示,在求M坐标时,亦可以通过构造“K型”相似,求出点M的坐标.

图7

图8


图9
生5:如图9所示,过点G作GM⊥P2C交CB于点M,作MH⊥x轴,通过构造“K型”相似求出点G的坐标.
设计意图:通过小组讨论得出结果,体现了课堂教学中生生互动的环节,在学生思维碰撞的过程中得出了“一题多解”的巧妙方法,在课堂展示思路环节过程中启发学生思维,真正实现了把课堂还给学生,学生成为课堂的主导.
师:关于问题2的求解.


图10

图11
生2:如图11所示,利用45°构造“K形”全等模型.过点A作AG⊥CP交PC的延长线于点G,过点C作CQ⊥GQ,过点G作GH⊥x轴,因为∠ACO+∠BCP=90°,所以∠ACG=45°,易得△AHG≌△GQC,求得点G的坐标,求出CP的解析式,联立抛物线方程求解.
教师总结:不管是利用三角函数还是相似三角形都是把角和边联系在一起,得到一些点和线的关系.希望学生在以后的学习过程中可以做到“经一题,解一题,题题皆宝藏;遇一题,化一题,题题是故人”.
2 教学反思
2.1 彰显函数复习课的特点
函数问题是最能体现“数形结合”思想的地方,通过一题入手,以基础简单模型为切入口,利用三角函数和构造相似三角形等手段,将几何问题转化为代数问题,实现了由数到形的突破.解题方法虽多样,但目的和方法都归为一类,即实现了函数问题数形结合的基本数学思想方法,在自主探究讨论中,由易到难,由浅入深,通过生生互动发展学生思维,潜移默化中达到了解一题、通一类的目的,极大地彰显了函数复习课的特点,突破了原有复习模式的禁锢,真正实现了把课堂还给学生的目的.
2.2 突出“一题一课”的优势
“一题一课”教学模式结合探究式教学手段,能有效培养学生的思维;尝试提问、自主改编能培养学生的创新能力.中考复习课要求学生对知识的理解要更加深刻,以本节课为例,学生在教师的引导下,由浅入深,由易到难,通过小组合作,在自主探究中不断地变式,通过一题多解等模式掌握二次函数中角度问题的基本研究方法和结论,这种方式往往比单纯回顾知识点更有效果.
教师改变复习课“讲题+做题”的做法, 给予学生自主生长的时间、空间与表达机会. 一题一课式的微专题复习课是专题复习一种有效形式, 教师在微专题复习课的教学中, 需要重构数学的教育价值, 关注数学本质, 可以由生长源(元问题)出发, 基于基础与经验, 在解决问题过程中不断产生新问题, 不断生长新的数学知识、方法、思维、经验. 让学生经历知识自主建构、方法感悟提炼、经验不断积累、思维不断提升的过程[2].
2.3 探究式教学发展学生的核心素养
数学教学应该落实发展学生核心素养的根本任务.复习课不能只为考试服务,应该以发展学生核心素养为最终目标,以长远的眼光为学生未来的发展奠基.探究式教学模式利用小组合作,通过学生自主探究、提出问题和解决问题的方式,锻炼了学生用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界的能力,发展了学生的核心素养,激发了学生学习数学的兴趣.

