孤岛新能源场站接入柔性直流高频振荡机理及抑制策略

苑 宾，厉 璇，尹聪琦，刘芮彤

（1.国网经济技术研究院有限公司,北京市 102209；2.国网辽宁省电力有限公司电力科学研究院,辽宁省沈阳市 110055）

0 引言

随着风电、光伏等新能源装机容量的不断提升以及海上风电的蓬勃发展,大规模新能源经柔性直流（MMC-HVDC,以下简称“柔直”）送出正逐渐成为新能源并网的重要技术手段之一［1］。大量电力电子变流器的使用正显著改变电力系统的动态行为,高比例新能源渗透与高比例电力电子化的“双高”电力系统高频振荡问题已经出现,并严重影响了系统安全可靠运行,是中国大规模新能源经柔直并网亟须解决的关键问题［2］。

国内外已经建成投运的柔直工程曾多次出现高频 振 荡 现 象［3］。 欧 洲 法 国-西 班 牙 联 网 工 程（INELFE）出现1 700 Hz 高频振荡现象,德国北海BorWin1 海上风电柔直并网工程出现300 Hz 左右高频振荡现象［4-5］,中国鲁西、渝鄂直流背靠背联网工程出现1 270、650、1 800 Hz 高频振荡现象［6-7］,张北柔直电网工程（以下简称“张北工程”）出现3 550、1 550、750 Hz 多个频率的高频振荡现象。高频振荡导致系统电压发散失稳,换流器闭锁跳闸,同时新能源场站部分滤波器设备因过大的高频谐波电压而损坏,亟须对高频频振荡机理进行研究,同时提出解决方案。

阻抗分析法是研究系统高频振荡机理与风险评估的重要方法,目前已有多篇文献通过阻抗分析法对柔直换流器的高频振荡问题进行研究。文献［8］提出了柔直换流器序阻抗模型的建模方法,提出了序阻抗模型用于系统稳定分析的判据。文献［9-10］研究了柔直换流器序阻抗数学建模方法,建立了两电平电压源换流器的序阻抗模型；文献［11-12］在此基础上考虑了模块化多电平换流器（MMC）内部动态过程,建立了序阻抗数学模型；文献［13］考虑了不同频率之间的耦合作用,建立了柔直换流器耦合阻抗数学模型。上述文献主要以柔直换流器精确阻抗建模为目标,分别建立了旋转坐标系下的dq阻抗模型、静止坐标系下的序阻抗模型以及考虑频率耦合特性的耦合阻抗模型,所建模型能够对柔直高频振荡的机理进行一定的解释,但与实际工程控制保护系统硬件在环扫频结果仍存在一定的差异。文献［6,14］在柔直换流器阻抗数学模型的基础上,考虑了柔直换流器控制链路延时对系统高频阻抗特性的影响,认为柔直换流器接入交流电网的高频振荡主要由控制链路延时引起,但对于控制中其他因素的影响研究不够全面。文献［7,15］针对渝鄂直流背靠背联网工程提出了柔直接入弱交流电网的高频振荡抑制方法。虽然渝鄂工程为柔直联网工程,但高频振荡产生机理相似,抑制策略有共通之处,可以借鉴。文献［16］研究了电压前馈环节对柔直换流器高频阻抗特性的影响,提出了鲁西直流背靠背联网工程高频振荡问题解决方案,但缺少针对孤岛新能源场站接入柔直的振荡问题详细分析。

本文以张北工程、如东海上风电柔直送出工程（以下简称如东工程）现场谐振现象为研究对象,揭示导致新能源经柔直送出系统高频振荡的核心机理。通过数学模型确定影响柔直换流器高频阻抗特性的关键因素,有针对性地提出了工程实用解决方案,并通过仿真及现场试验验证了方案的有效性。

1 张北、如东工程概况及高频振荡问题

张北工程、如东工程均为大规模新能源孤岛经柔直送出工程。张北工程将张北地区4 500 MW 的新能源功率送至北京地区与丰宁抽水蓄能电厂,如东工程将如东地区离岸距离100 km 的1 100 MW 海上风电送至江苏地区。

张北工程、如东工程在现场调试过程中均出现复杂的高频振荡现象。康保换流站在连接空载交流母线时产生3 550 Hz 高频振荡；在连接空载线路时出现1 550 Hz 高频振荡,如图1（a）所示；张北换流站在连接部分风电场以及空载线路时出现750 Hz高频振荡。

图1 孤岛新能源场站接入柔直高频振荡波形Fig.1 Waveforms of high-frequency oscillation caused by integration of islanded renewable energy station into MMC-HVDC system

如东工程海上换流站连接空载交流母线时出现2 000 Hz 高频振荡现象,如图1（b）所示；连接部分风电场时出现320 Hz 高频振荡现象。

高频振荡导致孤岛新能源换流站闭锁跳闸、新能源功率无法外送的情况。为解决大规模新能源孤岛经柔直送出的振荡问题,需要构建柔直换流器精确阻抗数学模型,对上述工程中高频振荡风险关键影响因素进行研究。

2 柔直换流器高频阻抗数学建模及关键影响因素

2.1 考虑序分量分离环节的柔直换流器阻抗数学模型

本文建立的柔直换流器阻抗模型中控制部分包括:电压外环控制、电流内环控制、环流抑制控制、序分量分离、采样延时、电压前馈滤波、电流反馈滤波、控制链路延时,一次系统模型考虑柔直换流器内部动态过程。柔直换流器阻抗数学建模过程详见附录A 第A1.1 节。

序分量分离环节能够有效地对50 Hz 电压、电流的正负序分量进行分离,且分离后电压、电流幅值和相位不变,但针对高频分量,该算法会导致电压、电流的幅值发生变化、相位发生偏移。在经过序分量分离算法后,电压正序分量瞬时值为vpa,其表达式为:

式中:V1为基频分量幅值；t0=5 ms,为序分量分离环节延时；ω为高频分量的频率；φ0为序分量分离带来的相位偏移；tdelay为相位变化等效滞后时间。

从式（1）可以看出,序分量分离环节导致正序电压的高频分量幅值、相位均发生变化,相当于在控制器的电压、电流输入环节增加了能够调节幅值、相位的滤波器,从而对柔直换流器高频阻抗特性产生较大的影响。以400～600 Hz 为例,表1 为不同高频分量在经过序分量分离算法后的幅值、相位变化程度。

表1 不同频率电压、电流分量经过序分量分离环节后的幅值和相位变化Table 1 Amplitude and phase changes of voltage and current components with different frequencies after sequence component separation link

在综合考虑序分量分离环节、测量回路延时后,进一步精确构建柔直换流器高频阻抗数学模型,如式（2）所示。构建方法以及数学模型的准确性验证详见附录A 第A1.1 节。

式中:Vs、Vc、Is、Ic分别为电压、电流分量幅值,下标s、c 分别代表自频率与耦合频率,顶标“˙”代表相量,“～”代表该相量的共轭；Z11、Z22代表同频率之间的自阻抗,Z12、Z21代表耦合频率之间的互阻抗。

2.2 柔直换流器高频阻抗简化数学模型

阻尼灵敏度是表征各一次设备、控制系统参数对柔直换流器阻尼水平影响程度的量化指标。阻尼灵敏度分析表达式如式（3）所示。

式中:α（ξ0,f0）为阻尼灵敏度；ξ0代表某一系统参数；Δξ为参数小信号量；f0代表某一频率点；Z为系统阻抗,即上述Z11、Z12、Z21和Z22；D为系统阻尼比,表达式为阻抗实部与阻抗幅值之比。

耦合阻抗主要影响低频段的振荡现象,因而本文重点考虑自阻抗的影响。耦合阻抗判据以及通过减小Z11阻抗相位超出90°的区间实现高频振荡抑制的理论依据详见附录A 第A2 章。

依据阻尼灵敏度分析,外环控制参数的影响仅限于500 Hz 以内频段,可知功率水平、锁相环控制参数对阻尼特性的影响仅限于50 Hz 附近的次超同步频段。电流内环控制参数对较宽频带的柔直换流器阻抗特性有较大影响。根据灵敏度分析结果对柔直换流器高频阻抗数学模型进行简化,灵敏度分析结果与简化过程详见附录A 第A1.2 节,最终可得阻抗矩阵如式（4）所示。

式中:R、L分别为换流器公共连接点至虚拟电位点的等效电阻、等效电感；∑Tdi为控制系统链路延时之和；φ0s、φ0c为序分量分离带来的相位偏移；ks、kc为序分量分离带来的幅值变化；kpin、kiin分别为内环比例-积分（PI）控制器的比例和积分参数；ss、sc分别为某一频率及其耦合频率的拉普拉斯算子。

2.3 影响柔直换流器高频阻抗特性的关键因素

由式（4）可知,影响柔直换流器高频阻抗特性的因素包括:主回路参数（R、L）、内环PI 控制器比例参数（kpin）、序分量分离环节、控制系统链路延时。根据柔直系统高频失稳判据可知,当柔直换流器阻抗相频特性存在大于90°的区域时,系统存在一定的谐振风险。对于表达式（4）中的Z11,导致其高频阻抗相频特性出现超出90°的原因主要包括分子中序分量分离环节、延时环节以及分母中延时环节使阻抗产生相位偏移。分母中延时环节（电压前馈环节）的存在使柔直换流器的相位特性在高频段出现0°～180°的波动,如图2（a）所示,而且延时越长,此波动越频繁,从而导致柔直换流器在多个频率范围存在谐振风险。为了消除控制链路延时对分母的影响,文献［6］提出了增加电压前馈环节非线性滤波器的抑制策略,其数学本质为消除了分母部分控制链路延时以及序分量分离环节的影响。增加前馈电压非线性滤波器后Z11的表达式为:

增加非线性滤波环节的柔直换流器阻抗如图2（a）所示,其高频阻尼特性得到了很大程度的提升,但由于分子部分仍然存在控制链路延时的影响（电流控制环）,仍存在超过90°的频段,系统仍存在高频振荡风险。

除了控制链路延时,序分量分离算法对柔直换流器的高频阻抗特性同样具有较大影响。根据式（5）可知,序分量分离环节相当于对柔直换流器高频阻抗相位附加了额外的角度,且随频率变化,角度在-45°～45°之间呈现周期性变化（如表1 所示）,从而造成高频段阻抗特性出现周期性波动,如图2（b）所示。相位波动程度与内环比例系数kpin相关,当kpin增大时,序分量分离算法导致柔直换流器高频阻抗相位波动增大,从而在某些频段增加了系统高频振荡的风险,即使不考虑序分量分离环节的影响,增大kpin同样使式（4）中链路延时导致的相位波动增大,增加了高频振荡风险。降低内环电流控制环节比例参数能够有效地提升系统高频阻尼特性,但伴随的是换流器响应特性变慢,动态特性以及故障穿越特性变差,一味降低并不是很好的解决思路。

图2 不同控制环节对柔直换流器阻抗特性的影响对比Fig.2 Comparison of influences of different control links on impedance characteristic of MMC

3 柔直换流器高频振荡问题解决方案

根据2.2 节以及2.3 节研究的结果可知,通过降低柔直换流器高频阻抗相位能够有效地增强系统阻尼特性。采用不同序分量分离算法能够抑制柔直换流器高频阻抗相位的波动,防止高频振荡。目前工程中采用的序分量分离算法除了延时5 ms 算法外,还包括dq解耦后带阻滤波、低通滤波方法。其主要原理为:正序、负序两路Park 变换环节同时对电压、电流分量进行坐标变换,对于不同序分量,当经过Park 变换后转化为100 Hz 的频率分量,进一步通过带阻滤波、低通滤波即可提取需要的序分量。

不同序分量分离环节对柔直换流器阻抗特性的影响如图3 所示。由图3 可知,更新序分量分离环节能够去除柔直换流器在高频段阻抗的相位波动,但由于增加滤波器,柔直换流器在中高频段的相位增大,从而恶化了中高频段的阻尼特性。因此,采用dq解耦配合带阻滤波、低通滤波的控制方式能够增强换流器在高频段的阻尼特性,但会对中高频段的阻尼特性产生恶化效果。

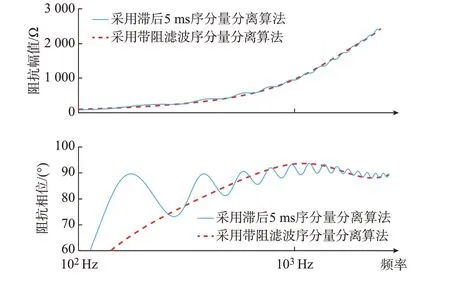
图3 不同序分量分离环节对柔直换流器阻抗特性的影响Fig.3 Influences of different sequence component separation links on impedance characteristic of MMC

通过采用增强滤波控制算法同样能够增强系统高频阻尼特性。增强滤波控制算法为原有直接电流控制方法的基础上增加电压前馈滤波与电流反馈滤波环节,其控制框图如图4 所示。其中,红色和绿色框线分别代表电压前馈滤波环节与电流反馈滤波环节；Vsd,ref、Vsq,ref分别为交流电压d、q轴分量整定值；Vsd,m、Vsq,m分别为交流电压d、q轴分量实测值（经过数字滤波）；Id,ref、Iq,ref分别为交流电流d、q轴分量整定值；Id、Iq分别为交流电流d、q轴分量实测值；Vva、Vvb、Vvc为阀侧虚拟电位点三相交流电压；Gd、Gq为内环PI 控制器参数；GP、GQ为外环比例积分控制器参数；Tv、Ti分别为电压、电流滤波环节的时间常数；Gt1、Gt3分别为极控、阀控链路延时；θ为锁相环输出角度。

图4 增强滤波控制算法控制框图Fig.4 Control block diagram of enhanced filter control algorithm

采用增强滤波控制算法的柔直换流器高频阻抗简化数学模型如式（6）所示:

从式（6）所示数学模型可知,增加电压前馈滤波环节能够降低控制链路延时以及序分量分离环节在阻抗特性分母中的影响。虽然无法像非线性滤波器一样将Z11中分母部分彻底消除,但通过增大Tv的取值能够降低滤波器截止频率,目前张北工程、如东工程中采用Tv=0.01 s,截止频率约为16 Hz,其滤波效果与非线性滤波器已经非常接近。电流反馈滤波通常采用一阶或二阶低通滤波方式,截止频率通常在160 Hz 附近,在高频段时其放大系数会迅速下降,从而降低控制链路延时以及序分量分离环节在阻抗特性中分子部分的影响。但在中低频段,此时放大系数下降程度不够,同时低通滤波器的延时特性又较为突出,从而导致中低频段相位特性较差,会增加中低频段系统振荡风险。阻抗特性对比如图5所示。

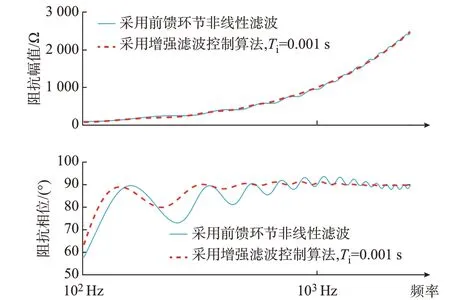
图5 采用增强滤波控制算法的柔直换流器阻抗特性Fig.5 Impedance characteristic of MMC using enhanced filter control algorithm

增强滤波方案需要针对柔直换流器主回路参数、控制特性以及交流系统或新能源系统阻抗特性综合考虑并进行参数设计。由一阶低通滤波器的幅值特性与相频特性可知,随着频率的提高,经过滤波器后的幅值显著下降,而高频谐波的相位滞后特性将变得更加显著。对于式（6）而言,显著下降的幅值特性使分母更接近于1,相位滞后特性即使更加明显,对于整体阻抗的负阻尼特性仍为抑制效果。同理,在式（6）中电流反馈一阶低通滤波同样通过其幅值特性能够降低控制链路延时、反馈、序分量分离等环节带来的负阻尼作用。通过增强滤波方案,柔直换流器的高频阻抗特性可更接近于R+sL,从而降低系统高频振荡风险。但增强滤波方案对中频段柔直换流器的阻抗特性产生一定的恶化作用,主要因为一阶低通滤波器在中频段（如200～500 Hz）的幅值衰减特性不够显著,同时相位滞后特性逐渐突出,存在增大中高频段振荡风险的问题,这是滤波器方案的通病。在工程中,通常根据具体孤岛新能源系统的情况、柔直换流器的一次系统参数与控制特性对滤波器参数进行优化。

考虑到控制链路延时、序分量分离环节延时以及电压前馈、电流反馈是导致系统产生高频振荡的最主要原因,对于连接孤岛新能源系统的柔直换流站,通过降低控制前馈、反馈程度,即采用弱反馈控制算法能够解决大范围频段内的高频振荡问题。弱反馈控制的控制框图如图6 所示。其中,Va、Vb、Vc为换流变压器网侧三相电压；Vd、Vq分别为换流变压器网侧电压d、q轴分量；Vvd,ref、Vvq,ref分别为阀侧虚拟电位点电压d、q轴分量整定值。

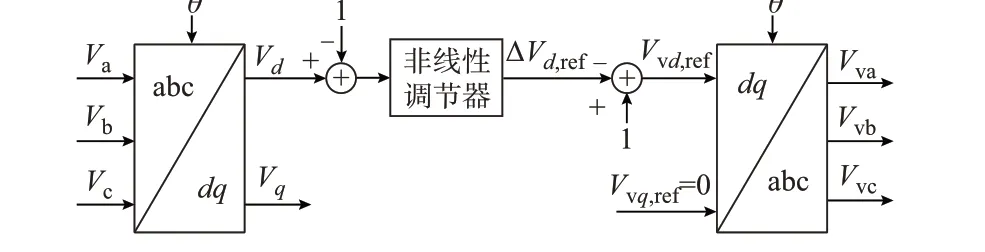
图6 弱反馈控制简化控制框图Fig.6 Simplified control block diagram of approximate feedback control

弱反馈控制中的非线性调节器原理为:当交流电压实测值Vd与1 p.u.的偏差超出一定范围后,非线性调节器输出电压变化量为ΔVd,ref,从而对电压调制波进行调节,使换流器输出电压能够保持在1 p.u.左右。非线性调节器简化表达式如式（7）所示。

弱反馈控制相当于取消了电压、电流反馈环节,即使一次系统中存在链路延时,从阻抗来看仍然不会引入负反馈带来的负阻尼问题,因而是解决高频振荡的有效方案。采用弱反馈控制的柔直换流器高频阻抗模型详见附录A 第A1.3 节。

弱反馈控制方法同样存在一些问题:1）只适用于孤岛新能源系统。该控制方法无锁相环,因而只能作为简单的构网型控制,无法实现电网电压跟随；2）无法实现故障电流抑制。由于无内环电流控制,无法对交流故障电流进行抑制,交流故障无法穿越；3）无暂态调节能力。当孤岛系统功率水平发生大幅波动时,由于无电流内环控制,难以实现快速响应。通过对控制环节进行优化,实时监测交流电网电压变化情况,当交流电网单相或整体出现较大跌落时,说明系统发生故障,此时投入内环电流控制环节,起到抑制故障电流的效果。

4 新能源经柔直送出工程高频振荡解决方案验证

本章以张北工程与如东工程为例,分别搭建了张北工程、如东工程PSCAD 仿真模型,通过仿真模型对振荡抑制策略进行验证。

4.1 增强滤波控制算法的有效性验证

张北工程柔直换流器在接入空载线路以及风机时产生高频振荡现象,振荡频率为1 550 Hz。分别对柔直换流器以及新能源系统的阻抗特性进行对比,对比结果如图7 所示。

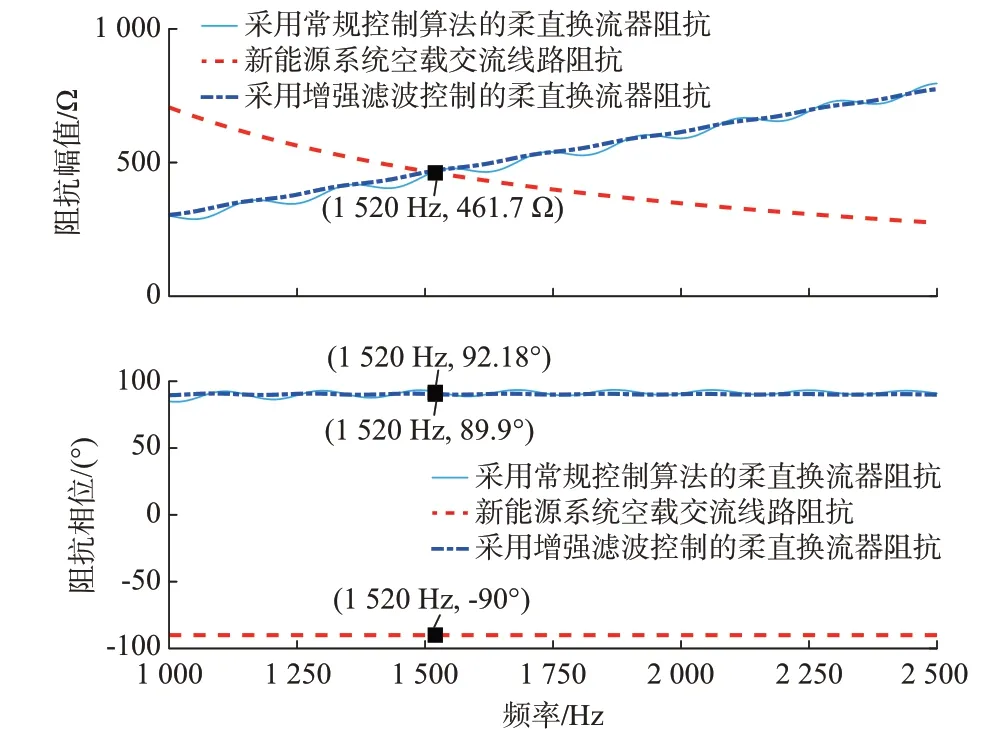
图7 柔直换流器与新能源场站空载线路阻抗特性对比Fig.7 Comparison of impedance characteristics between MMC and no-load line of renewable energy station

通过对比可知,柔直换流器与新能源系统在1 520 Hz 频率点高频阻抗幅值Z11存在交点,此时相位差为182.18°,系统存在高频振荡风险。通过仿真与现场调试均发现1 550 Hz 附近的高频振荡现象。通过优化控制,采用增强滤波控制算法,其中,电压前馈环节采用截止频率为15.9 Hz 的一阶低通滤波,电流反馈环节采用截止频率为79.5 Hz 的一阶低通滤波,仿真与现场实测发现系统均能够稳定运行,如图8 所示。

图8 孤岛新能源场站接入柔直1 550 Hz 高频振荡仿真波形Fig.8 Simulation waveforms of 1 550 Hz highfrequency oscillation caused by integration of islanded renewable energy station into MMC-HVDC system

4.2 弱反馈控制算法的有效性验证

如东工程海上柔直换流站在短时解锁后发生2 000 Hz 高频振荡现象。该工况没有空载交流线路,为柔直换流器与换流变压器对地、交流母线对地杂散电容阻抗匹配形成的高频振荡现象,同时换流变压器阀侧断路器、电缆等设备对地杂散电容会恶化柔直负阻尼特性。与厂家核实换流变压器网侧对地杂散电容接近0.18 μF,交流母线对地杂散电容一般在2 nF 左右。对柔直换流器、换流变压器对地杂散电容的阻抗特性进行对比,对比结果如图9所示。

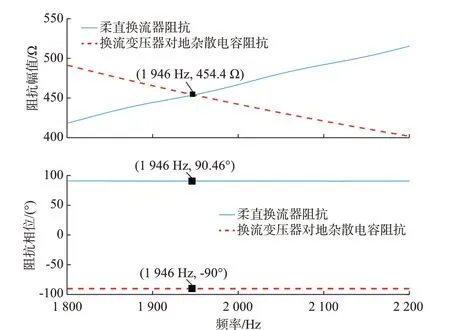
图9 柔直换流器与换流变压器对地杂散电容阻抗特性对比Fig.9 Comparison of impedance characteristics between MMC and earth stray capacitor of converter transformer

如东工程柔直换流器采用了截止频率为15.9 Hz 的电压前馈一阶低通滤波与79.5 Hz 的电流反馈一阶低通滤波,高频阻抗特性已接近纯感性,阻抗角为90.46°,但由于对地杂散电容为纯容性系统,因而仍存在高频振荡风险,阻抗相位差为180.46°。此时,采用增强滤波控制算法仍难以彻底将柔直高频阻抗特性限制在90°以下,因而采用弱反馈控制算法解决高频振荡问题。通过仿真与现场实测发现系统均能够稳定运行,如图10 所示。

图10 孤岛新能源场站接入柔直2 000 Hz 高频振荡波形Fig.10 Waveforms of 2 000 Hz high-frequency oscillation caused by integration of islanded renewable energy station into MMC-HVDC system

弱反馈控制算法无电流控制环,因而不具备故障限流能力。为实现交流故障穿越,需要增加内环限流控制器,通过判定交流电网是否处于故障状态投切限流控制器。

4.3 控制算法适用场景总结

增强滤波控制算法主要解决2 000 Hz 以内的高频振荡问题。通过理论分析与仿真测试结果表明,由于2 000 Hz 以内柔直换流器阻抗相位特性波动较大,增强型滤波能够使2 000 Hz 以内的高频段阻抗相位特性较大程度地向90°靠近,抑制高频振荡的效果较明显。同时,增强滤波控制算法对孤岛系统、联网系统无要求,因而既可以适用于柔直换流器接入交流电网,也可以适用于接入孤岛新能源系统或无源电网。

弱反馈控制算法能够解决所有高频振荡问题。通过理论分析可知,弱反馈控制类似于取消了电压、电流反馈环节,保证柔直换流器不出现负阻尼频段。但弱反馈控制只能适用于接入孤岛新能源系统或无源电网,不适用于联网换流站。同时,由于取消了反馈环节,交流系统发生故障时电流上升速度较快,故障穿越失败。考虑到弱反馈控制的缺陷,通常发生交流系统故障后会短时切换至增强滤波控制解决问题,切换过程详见附录B 第B1 章。

针对实际工程,如果考虑柔直换流器具备一定控制能力,可采用控制切换的方式。当新能源场站发出功率较低时,采用弱反馈控制保持系统稳定；当新能源场站发出功率高于一定水平后,采用增强滤波控制算法保持控制能力,切换过程详见附录B 第B2 章。

5 结语

本文描述了张北、如东工程孤岛新能源场站接入柔直换流器的高频振荡现象,研究了其高频振荡的机理。在一定程度上对高频阻抗数学模型进行简化,更直观地确定影响柔直换流器高频阻抗特性的关键因素并提出工程解决方案。经电磁暂态仿真及工程现场试验验证了控制策略的有效性,得到如下结论:

1）孤岛新能源场站接入柔直换流器的高频振荡的主要原因为控制链路延时结合前馈、反馈控制使柔直换流器产生感性负阻尼特性,与新能源孤岛系统容性特性匹配发生高频振荡。

2）影响柔直换流器高频阻抗特性的关键因素除控制链路延时外,还包括序分量分离算法、内环控制器比例参数、一次主回路参数。通过优化序分量分离算法能够在一定程度上降低系统高频振荡风险。

3）电压前馈环节、电流反馈环节增加相应滤波器从阻抗数学表达式上是防止系统产生高频振荡的有效手段,即增强滤波控制方法。但由于数字滤波器带宽不能无限降低,控制器带宽过低会导致柔直换流器响应速度大幅下降,同时不合适的带宽对柔直换流器中频段的阻抗特性产生恶化作用,相关滤波参数需要综合考虑多方面因素优化设计。

4）采用弱反馈控制算法能够彻底去除前馈、反馈控制环节,解决高频振荡问题。但柔直换流器不具备故障穿越能力以及暂态过程的调节能力,因而需要进一步优化设计以满足相关要求。同时,弱反馈控制为构网型控制模式,只适用于孤岛新能源经柔直送出系统。

目前,虽然弱反馈控制能够有效解决柔直换流器孤岛连接新能源场站的高频振荡问题,但在故障穿越过程中,由于内环限流环节的投入,仍不可避免产生了振荡现象。本文提出的解决方案仅对控制系统进行优化,但高频振荡之所以能够发生的一个重要原因是全控型电力电子器件以及所构成的换流器具备足够高的电压输出频率,为高频振荡提供了发展空间。接下来,针对此类“双高”电力系统高频振荡的抑制方法研究应重点集中在降低换流器能够输出的电压频率方面。但降低输出电压频率同时说明换流器的动态响应速度降低,因而工程设计中需要综合考虑。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。