Iterative Phase Noise Suppression for Full-Duplex Communication Systems

Pengxin Guan,Yiru Wang,Hongkang Yu,Yuping Zhao,*

1 School of Electronics Engineering and Computer Science,Peking University,Beijing 100871,China

2 Wireless Product Research and Development Institute,ZTE Corporation,Shenzhen 518057,China

Abstract: Oscillator phase noise is one of the bottlenecks that limits the self-interference(SI)cancellation capability of full-duplex systems.In this paper,we propose a method for the suppression of common phase error (CPE) and intercarrier interference (ICI)induced by the phase noise in full-duplex orthogonal frequency division multiplexing(OFDM)systems.First,we regard the effect of CPE as a portion of the SI channel and perform estimation,reconstruction and elimination in the time domain.Then,the ICI signal is estimated and suppressed in the frequency domain.Additionally,by analysing the performance of proposed algorithm,we further develop an iterative mechanism to reduce the parameter estimation error and improve SI cancellation capability.Simulation results show that the proposed method has a significant SI cancellation capability improvement over the traditional SI cancellation schemes.

Keywordst: full-duplex; self-interference; phase noise;suppression

I.INTRODUCTION

By transmitting and receiving signals over the same time and same frequency band,full-duplex(FD)communications can yield double the spectral efficiency of current half-duplex communications [1—3].In addition,full-duplex technology can also improve communications security and reduce communications delay [4],which is promising for future mobile communications [5,6].However,the presence of strong self-interference(SI)due to possible coupling and reflections in the transceiver is the biggest challenge for practical application of full-duplex communication systems.The Interference cancellation is an important topic in mobile communications [7].Normally,the self-interference cancellation (SIC) schemes can be primarily categorized into passive suppression and active suppression.Specifically,passive SIC is usually designed in the propagation domain,which eliminates SI signal by increasing antenna isolation or using a circulator[8,9].Active SIC schemes estimate and construct a replica of the SI signal in the analog domain[10,11]and digital domain[12—14],and then subtract it from the received signal.In practice,passive and analog SIC can only reduce SI partly,and residual SI should be suppressed in digital domain.Hence,digital SIC algorithms need to be carefully designed to further improve SIC capability of system.

However,in practice,SIC capability is not ideal due to the impairments produced in transceiver components,such as the oscillator phase noise,the nonlinearity of the amplifier and the in-phase/quadrature imbalance.Particularly,phase noise is typically a limiting factor of SI cancellation in full-duplex orthogonal frequency division multiplexing(OFDM)systems,which introduces common phase error(CPE)and intercarrier interference(ICI)[15,16].

A phase noise suppression architecture based on a digital control delay module is proposed to mitigate this issue,but it increases system hardware overhead[17].In addition,this architecture is not feasible when the transmitter and receiver have separate oscillators,which is also a valid scenario in relay type devices[15].Another scheme based on minimum mean square error(MMSE)has been proposed but assumes both the perfect SI channel state information and the statistical properties of the phase noise are known,and is thus impractical[18].Another SI cancellers with blind signal processing have been proposed[19].This method first used the blind method to eliminate the SI signal and then recover the intended signal,which need the accurate symbol synchronization.Additionally,the traditional time domain self-interference cancellation (TD-SIC) method and frequency domain selfinterference cancellation(FD-SIC)scheme in[20]and[21] estimate the SI channel in the time domain and frequency domain respectively,reconstruct the SI signal,and subtract it from the received signal.However,these two schemes compensate only for CPE and ignore the effect of ICI induced by phase noise,which limits the SI cancellation capability.

Based on the above motivation,we develop a novel phase noise suppression scheme for full-duplex OFDM system.Unlike existing methods,our proposed method can suppress both the CPE and ICI without knowledge of perfect SI channel state information and any statistical property of the phase noise.Specifically,this paper presents the following contributions:

・ We derive the equivalent channel (EC),which is composed of the effect of CPE and SI channel.Based on the estimation of the EC and ICI coefficients,both the CPE and ICI signals are reconstructed and suppressed.

・ We analyze the limitations of the proposed method and further develop an iterative mechanism to reduce the parameter estimation error and improve the SI cancellation performance.

・ Simulation results show that the proposed algorithm only needs three iterations to converge and improves SI cancellation capability markedly compared to the traditional schemes.

The remainder of this paper is organized as follows.In Section II,a detailed model of the SI signal with the phase noise in full-duplex OFDM system is provided.The proposed estimation and cancellation scheme are presented in Section III.In Section IV,the performance of the proposed scheme under different scenarios is analyzed with baseband signal simulations.Finally,this paper is concluded in Section V.

Notation: We use(∗)to denote convolution,(·)Tto denote transpose,(·)Hto denote conjugate transpose and E[·]to denote expectation.Time domain variables are represented as lowercase letters,while frequency domain variables use uppercase.Furthermore,bold lowercase letters denote vectors.

II.SYSTEM MODEL

Consider a full-duplex OFDM transceiver as shown in Figure 1.The frequency domain transmitted information{X(k)}is performed on Inverse Discrete Fourier Transformation to obtain time domain signalx(n).Then,a cyclic prefix is added to the beginning ofx(n).The digital baseband signalx(n)is converted to an analog baseband signalx(t) by the digital-toanalog converter(DAC).By mixing with the transmitter oscillatorφT(t)=ej[2πfct+θT(t)]whereθT(t) is the phase noise at transmitter andfcis the carrier frequency,the radio frequency signal can be given as

wherehSI(t)andw(t)represent the practical SI channel impulse response and the additive Gaussian noise.To focus on SI cancellation,the intended signal is omitted for notational convenience because it affects the SI cancellation in the same way as receiver noise does[16,17].

The analog cancellation(AC)is initially used for SI suppression to avoid receiver saturation.In general,AC methods use known pilot signal to estimate the SI channel in the analog or digital domain,and then reconstruct the replica of SI signal in analog domain based on the known transmitted signal and subtracted it from the received signal.We assume that the estimated channel in AC stage isa(t).Using the known transmitted signalanda(t),the reconstruction signal can be written as∗a(t) and is then subtracted from the received signal.Thus,the received signal after AC stage can be written as

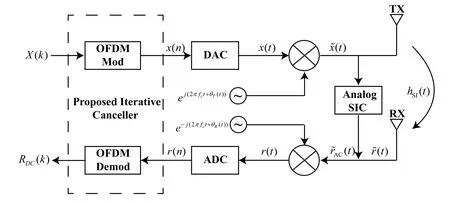
Figure 1.Block diagram of full-duplex OFDM transceiver.

whereh(t)represents the effect of the SI channel and AC stage.We defineh(t)to be the residual SI channel for convenience in a later paper.

After AC stage,the receiver RF signal is converted to the baseband signal by mixing the receiver oscillatorφR(t)=e−j[2πfct+θR(t)],whereθR(t) is the receiver phase noise.Further,the signal at the analog-to-digital converter output is the digital baseband signal which can be written as

whereh(n),θT(n),θR(n) andw(n) are the discrete version of the residual SI channel,the transmitter phase noise,the receiver phase noise,and the receiver noise,respectively.

By performing Discrete Fourier Transform (DFT)on both sides of (4),the frequency domain received signal can be given by

wherek=0,...,N −1 is the subcarrier index,Nis the subcarrier number,W(k) is the frequency domain noise,{H(k)}is the frequency SI channel response.TheδTandδRareNpoint DFT of the transmitter and receiver phase noise respectively,which can be given as

Equation (a) is based the fact that the 3-dB bandwidth of the oscillator power spectral density is small sufficient compared to the coherence bandwidth of the SI channel [18].Theδk−lis the DFT coefficients of the combined transmitter and receiver phase noise calculated as the circular convolution ofδTandδR[18].When transmitter and receiver share the same oscillator,θT(n)=θR(n),and when separate oscillators are used,θT(n)andθR(n)are independent.Based on(5),phase noise in FD OFDM systems introduces the CPEδ0,which affects all subcarriers,and ICI,which leaks the subcarrier power into other subcarriers.Note thatδ0is a special case ofδk−lwhenkis equal tol.

III.PROPOSED ALGORITHM

3.1 Suppression of the CPE

First,with regard to CPE as a portion of the SI channel,the frequency domain and time domain equivalent channel are defined asHEC(k)=δ0H(k) andhEC(n)=δ0h(n).Note thatHEC(k)isNpoint DFT ofhEC(n).For the OFDM system,the received signal in the time domain is represented as the convolution of the transmitted signal and the channel impulse response,and the received signal in the frequency domain is represented as the multiplication of transmitted frequency domain signal and the DFT of channel impulse response.Then the approximate time domain representation of(5)is given as

where the first item is the equivalent time domain expression of CPE signal andγICI(n) is the equivalent time domain expression of ICI signal.

The time domain convolution in(7)can also be expressed as a matrix multiplication,i.e.

where r=[r(ls),r(ls+1),···,r(ls+L1−1)]Tis the receiver signal vector of lengthL1and the starting sample indexls,hEC=[hEC(0),hEC(1),···,hEC(L −1)]Tis the equivalent channel with the number of tapsL,γICIand w are equivalent time domain expression of ICI signal vector and receiver noise vector.The matrix X is formed using the known transmitted signal samplesx(n),which is given as

ConsideringγICIas noise,the equivalent channel hECis estimated by the least-squares method as

Using the estimation of EC and known transmitted signals,the CPE is reconstructed and subtracted from the received signalr(n)given in(7)as follows

3.2 Suppression of the ICI

Based on(5)and the definition ofHEC(k),we can get frequency domain representation ofr1(n)as follows

Note thatκk−l=δk−l/δ0is the newly defined ICI coefficients andχ(k) is the residual CPE due to estimation error.In order to suppress the ICI,the ICI coefficients must be estimated.First,we calculateψ(k)=X(k)(k)using(k)and known transmitted frequency domain signalX(k).Then,equation(12)can be transformed into a matrix form as

where R1=[R1(lp),R1(lp+1),···R1(lp+L2−1)]Tis the frequency domain signal vector of lengthL2and the starting sample indexlp,κ=[κM/2,···,κ2,κ1,κ−1,κ−2,···,κ−M/2]Tis the estimated ICI coefficients with the orderM,V is the other not estimated ICI signal vector beyondM.Additionally,χand W are the corresponding sample vector of the residual CPE signal and receiver frequency domain noise.The matrixφis shown as follows

The least-squares algorithm minimizes the sum of squared residuals||R1||2,and the unknown ICI coefficients can be estimated as

Then we can reconstruct the ICI signaland subtract it fromR1.The signal with ICI suppression can be written as

whereRDC(k) represents the signal after digital SIC stage.

3.3 Performance Analysis

For the suppression of the CPE,we first estimate the equivalent SI channel hECbased on equation (10).Then,the estimation error of hECcan be written as

Further,we can obtain the power of residual CPE due to the estimation error as follows

whereEsis the transmission power,U is equal to(XHX)−1XHfor notational convenience.The equation (b) is based on the fact that the ICI signal and Gaussian noise are independent,and the mean value of noise is equal to 0.Based on equation (18),we can know that the existence of the ICI signal causes the estimation error of hECand leads to the residual CPE signal.Note that UHU is a positive semidefinite matrice,which means the functionγHICIUHUγICIis convex with respect toγICIand it is equal to 0 if and only ifγICI=0.If the ICI signal can be estimated and subtracted when we suppress the CPE,the power of the residual CPE signal will be reduced.

For the suppression of the ICI,we first estimate the ICI coefficientsκbased on equation (15).Then,the estimation errorκcan be written as

On the one hand,the presence of ICI signal lead to the estimation error of EC based on equation(17).On the other hand,the inaccurate EC will affect the accuracy of matrixφand cause the residual CPE signal,resulting in the estimation error of ICI coefficients based on equation (19).Due to the existence of estimation error,the CPE and ICI signals cannot be reconstructed and eliminated accurately from the received signal.

3.4 Iterative Improvement

Based on the above motivation,we propose an iterative algorithm to further improve the estimation accuracy of parameters and SI suppression performance of system.The algorithm is expressed in Algorithm 1,wherePis maximum number of iterations and [·](i)represents the result ofi-th iteration.

In each iteration,we first subtract the reconstructed ICI signal in the latest iteration from received signal,and estimate EC based on(10).Then,the higher accuracy EC is used to reconstruct and eliminate the CPE based on formula (11).The more preciseκis then obtained with (15).Finally,the ICI signal is reconstructed based on (16) using the new estimation results for the next iteration.The accuracy of EC and ICI coefficients increase with every iteration.After a certain number of iterations,both CPE and ICI can be accurately reconstructed,and subtracted from received signal.

Algorithm 1.Iterative phase noise suppression for fullduplex communication systems.Input: received signal {r(n)}N−1 n=0,maximum number of iterations P,ICI coefficients order M Output: signal after digital SIC{RDC(k)}N−1 k=0 1: Initialize the reconstructed ICI signal γ(0)ICI(n)=0 for all samples 2: for p=1,...,P do 3: Subtract the reconstructed ICI signal in the latest iteration: r(p)0 (n)=r(n)−γ(p−1)ICI (n)4: Calculate the estimate of EC by (10):h(p)EC=(XHX)−1XHr(p)0 5: Eliminate CPE by(11):r(p)1 (n)=r(n)−x(n)∗h(p)EC(n)6: Calculate ψ(p)(k)=X(k)(p)EC(k)7: Calculate the estimated of the ICI coefficient by(15): κ(p)=(φ(p)Hφ(p))−1φ(p)HR(p)1 8: Reconstruct ICI signal:Γ(p)ICI(k)=N−1images/BZ_241_367_1449_415_1495.png l=0,=k κ(p)k−lψ(p)(l)9: end for 10: Calculate RDC(k)=R(P)1 (k)−Γ(P)ICI(k)

Since the number of samples used for the estimation of the EC and ICI coefficients is limited and the additive Gaussian noise in system will lead to estimation errors,as the number of iterations increases,the parameter estimation accuracy will reach a certain level.Further,the power of the residual SI signals after digital SIC will be convergent,which means that the proposed iterative algorithm will be convergent.

3.5 Complexity Analysis

We compare the main computational complexity of proposed methods and conventional approaches.

・ The main calculation complexity of TD-SIC scheme isO(L3) multiplications because it only needs to estimate the SI channel in time domain.

・ The main calculation complexity of FD-SIC scheme isO(N) multiplications.Note thatNis the number of subcarriers.

・ For the proposed algorithm,the main calculation complexity is due to the matrix inversion in equation (10) and equation (15),which requireO(P(L3+M3))multiplications.

Fortunately,the inverse of the matrix XHX in equation(10)can be pre-computed and stored because the transmitted signals are known.Since the matrix XHX is a Hermitian matrix,there areL2real numbers need to be stored.Assuming that we use double-precision floating point format to store data,a total of 64L2bits of storage resources are requied.After the simplification,the main complexity of the proposed algorithm isO(P(M3)) due to the matrix inversion in ICI elimination stage.It is worth noting that our proposed algorithm only needs three iterations to converge,which means that a lot of computational complexity is not required.Moreover,simulation results show that a lowerMcan achieve significant performance,soMcan be appropriately selected according to the affordable complexity of the actual system.

IV.SIMULATIONS

4.1 Simulations Conditions

We consider a full-duplex OFDM system with 256 subcarriers,where the subcarrier spacing is 60 kHz and the sampling frequency is 15.36 MHz.The level of passive SIC and AC obtained are set to 30dB for the main tap[15,16].Then,the power delay profile of the Rayleigh multipath SI channel has four taps with values of 0,−5,−10,−15 dB for delay of 0,1,2 and 4 samples following the SI channel assumptions in[15].The propagation delaytdis set as 5 samples[16].

In this paper,the phase noise is modelled as a Wiener process,which is widely used in free-running oscillators[15].The phase noise at samplenis related to the previous sample asθ(n)=θ(n −1)+η,whereηis a Gaussian random variable with zero mean and varianceσ2=4πf3dBTs,andTsis the sampling interval.The termf3dBis the 3 dB coherence bandwidth of the Lorentzian spectrum for the oscillator,characterizing the quality of the oscillator,which indicates that a larger 3 dB bandwidth tends to yield more phase noise.In addition,ls,L1,lpandL2are set to 5,230,20 and 150 respectively in simulations.

For comparison,the traditional TD-SIC,FD-SIC and MMSE method in [18] are considered.The selfinterference cancellation ratio(SICR)is used to measure the digital cancellation capability[22]:

4.2 Simulations Results

In Figure 2,the SICR performance of the proposed iterative algorithm in both common oscillator and separate oscillators scenarios is shown with different number of iterations,where the interference-to-noise ratio(INR)is set to 50 dB andf3dBis set to 15 Hz.The INR is an important indicator to measure the strength of the SI signal,which denotes the interference-to-noise ratio,i.e.,the power ratio of the received digital SI signal after the analog SIC and noise.The estimation order of ICI coefficientsMis set to 80.In these two scenarios,if the number of iterations increases from one to three,the SICR of the proposed scheme is significantly improved due to the improvement of parameter accuracy.This indicates that the iterative process is effective and can improve SI cancellation capability.As the number of iterations continues to increase,the SICR reaches saturation because the performance of proposed algorithm is limited by some parameters,such as estimation order of ICI coefficientsMand the number of signal samples used for estimation.In addition,the simulation results also show that only a few iterations are needed to achieve a satisfactory performance,which means that too much computational complexity is not needed.Therefore,we apply three-time iterations for the parameter estimation process in a later paper because the proposed scheme can achieve sufficiently high cancellation performance with this setting.

We evaluate the performance of the proposed algorithm in the case of different estimation orders of the ICI coefficientsM.Figure 3 shows the SICR of both the proposed and conventional approaches where the INR is set to 50 dB,andf3dBis set to 15 Hz.The SICR of the proposed method increases as the estimated orderMbecause if we estimate more ICI coefficients,more accurate ICI signals can be reconstructed and eliminated.Thus,our algorithm with a properMyields significant improvement in performance compared to traditional methods,regardless of if a common oscillator or separate oscillators are used.

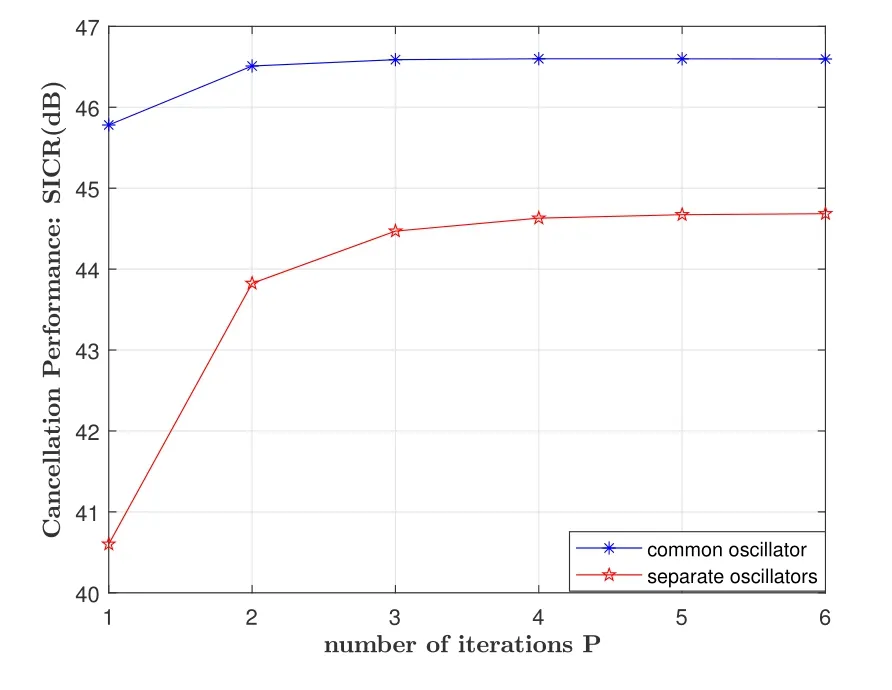
Figure 2.Performance of the proposed method with different number of iterations.

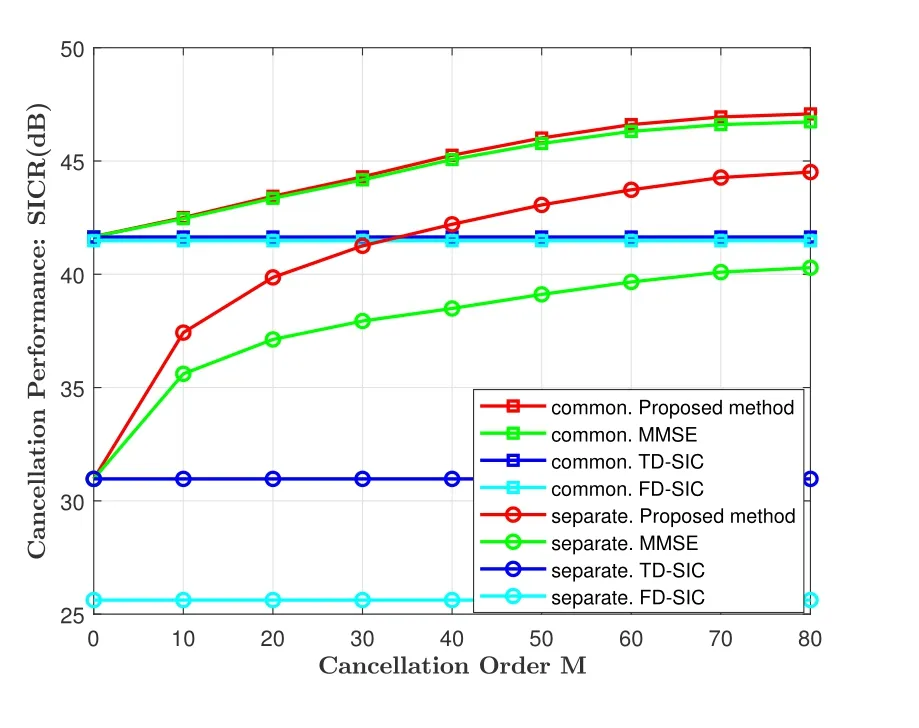
Figure 3.Digital SI cancellation performance with different cancellation order.

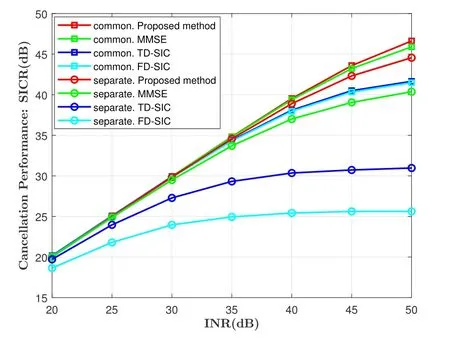
Figure 4.Digital SI cancellation performance with different INR.

The SI cancellation capability of proposed scheme and traditional methods with different the INR are shown in Figure 4,where the phase noise 3-dB coherence bandwidthf3dBis set to 15 Hz.The estimation order of ICI coefficientsMis set to 80.For a givenf3dB,the performance of all methods increase with INR,and the proposed method achieves the greatest cancellation capability in both common oscillator and separate oscillator scenarios.In particular,for scenarios with the separate oscillators,the proposed iterative algorithm increases performance markedly compared to traditional methods.It is worth noting that the performance of our algorithm is better than that of MMSE scheme due to the relationship between CPE and ICI is considered.

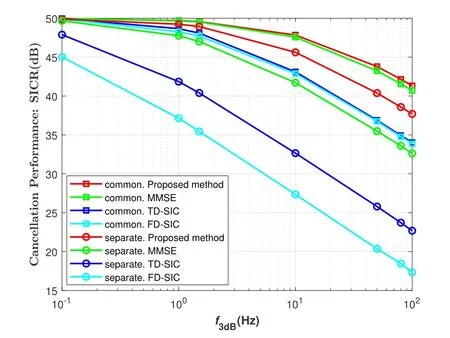
Figure 5.Digital SI cancellation performance with different f3dB.

In Figure 5,we compare the performance of the three methods with differentf3dB,where INR is set to 50 dB.The SICR of all methods decreases as the 3-dB bandwidth increases because a larger 3-dB bandwidth has larger damage to the systems.However,the SICR of the proposed algorithm decreases more slowly as the 3-dB bandwidth increases and has a significant performance advantage compared to the other two methods.The simulation results also indicates that the proposed algorithm can also be used for lowquality oscillator scenarios,which will reduce the cost and power consumption of the system.

V.CONCLUSION

In this paper,we develop a new solution to selfinterference cancellation in full-duplex OFDM systems with phase noise.First,we propose to treat the CPE induced by the phase noise as a portion of the self-interference channel and define it as the equivalent channel.Then,we complete the estimation,reconstruction and elimination of CPE in the time domain.Next,the ICI signal is estimated and suppressed in the frequency domain.After analyzing the limitations of these two suppression stages,we further introduce an iterative method to further increase the estimation accuracy of EC and ICI coefficients,and then improve the digital SI cancellation capability.The simulation results verify that the proposed algorithm has significant advantages over the traditional algorithms with either a common oscillator or separate oscillators with different INR andf3dB.In addition,power amplifier nonlinearity and inphase/quadrature imbalance also impact the SIC performance of the system.Therefore,we will study how to jointly suppress the influence of phase noise,PA nonlinearity and IQ imbalance on SIC performance in future.

ACKNOWLEDGEMENT

This work was supported by National Key R&D Program of China under Grant No.2020YFB1805102.