Channel Capacity and Power Allocation of MIMO Visible Light Communication System

Shuai Ma,Ruixin Yang,Guanjie Zhang,Hang Li,Wen Cao,Linqiong Jia,Yanyu Zhang,Shiyin Li,*

1 Peng Cheng Laboratory,Shenzhen 518055,China

2 School of Information and Control Engineering,China University of Mining and Technology,Xuzhou 221116,China

3 Shenzhen Research Institute of Big Data,Shenzhen 518172,China

4 School of Electronics and Control Engineering,Chang’an University,Xi’an 710064,China

5 School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

6 National Digital Switching System Engineering&Technological Research Center,Zhengzhou 450000,China

Abstract: In this paper,the channel capacity of the multiple-input multiple-output (MIMO) visible light communication (VLC) system is investigated under the peak,average optical and electrical power constraints.Finding the channel capacity of MIMO VLC is shown to be a mixed integer programming problem.To address this open problem,we propose an inexact gradient projection method to find the channel capacity-achieving discrete input distribution and the channel capacity of MIMO VLC.Also we derive both upper and lower bounds of the capacity of MIMO VLC with the closed-form expressions.Furthermore,by considering practical discrete constellation inputs,we develop the optimal power allocation scheme to maximize transmission rate of MIMO VLC system.Simulation results show that more discrete points are needed to achieve the channel capacity as SNR increases.Both the upper and lower bounds of channel capacity are tight at low SNR region.In addition,comparing the equal power allocation,the proposed power allocation scheme can significantly increase the rate for the low-order modulation inputs.

Keywordst:visible light communication;MIMO;discrete constellation inputs;power allocation

I.INTRODUCTION

As the era of Internet-of-things(IoT)comes,the conventional radio-frequency (RF)-based networks are facing spectrum crisis and high speed data-rates requirements to support massive devices[1,2].With extensive license-free spectrum,visible light communication (VLC) has emerged as a promising technology for indoor IoT applications[3].By employing the simple intensity-modulation-direct-detection(IMDD),VLC can simultaneously provide the data transmission and the illumination,and owns many advantages such as high data rates,no electromagnetic interference,low cost,energy efficiency and inherent security[4].

To meet the surge of data traffics,the multiple-inputmultiple-output (MIMO) VLC system has gained increasing research interests,since the MIMO technique,realized with multiple light-emitting diodes(LEDs) and multiple photodiodes (PDs),can apparently boost the data rate[5].Note that the channel capacity of VLC MIMO has not been found to be exclusively discussed.However,through singular value decomposition(SVD),the MIMO always can be equivalent to some parallel single-input-single-output(SISO)sub-channel [6].Due to the human eye safety and practical illumination considerations,the peak and average optical power should be bounded[7].In these constraints,it has been proved that the SISO channel capacity achieving distribution is a discrete distribution with finite support set[8—10].Meanwhile,it is a mixed integer programming optimization problem to find the optimal distribution,i.e.,to determine the number,position and probability of the mass point,which always is hard to characterize explicitly[11].

So far,the channel capacities of SISO and multipleinput-single-output (MISO) VLC systems have been extensively studied,and various upper bounds[12—17]and lower bounds [12—14,17] have been derived to approximate the capacity at high signal-to-noise-ratio(SNR) or low SNR regions.It should be pointed out that such results cannot directly be extended to MIMO VLC systems,since the MIMO VLC systems can simultaneously support multiple data streams.

Recently,some works investigated the channel capacity of MIMO optical wireless communication channels.The authors in [18] provided upper and lower bounds by either relaxing or reducing the constraints of inputs,respectively.In [19],the authors studied the capacity of parallel channels in the low SNR region,and the optimal intensity allocation was presented.The asymptotic capacity results in high SNR region are established in [20] for full column rank MIMO optical wireless channel.In[21,22],the authors proposed both upper and lower bounds of the capacity of optical wireless channels,which have a small gap between two bounds at high SNR.The capacity of the MIMO channel is characterized in [23]for the low-SNR regime,where a maximally correlated vector-binary distribution can achieve capacity at low-SNR.With only amplitude constraints,both upper and lower bounds of MIMO channels were proposed in[24,25],which are tight in the high amplitude regime.For the scenario with more transmit than receive antennas,the authors in[26]derived both lower and upper bounds on the capacity of MIMO optical wireless channel,which are tight at high SNR.

To the best of our knowledge,the channel capacity of MIMO VLC channel for all SNRs has not been found in the existing literature.In this paper,we aim to find the capacity of MIMO VLC channel with peak optical power,average optical power,and electrical power constraints.The main contributions of this paper are summarized as follows:

・ We propose an inexact gradient projection scheme to find the channel capacity for all SNRs.In particular,through SVD,the MIMO VLC channel can be transformed into the parallel SISO sub-channels,and the channel capacity of MIMO channel is equivalent to the sum of the subchannels capacity.When the peak and average optical power is limited,the capacity-achieving distribution is a discrete distribution with the finite support set,however,the problem to find it always is a a non-convex mixed integer programming problem,and neither the objective function nor its gradient has the analytical expression.To tackle this problem,an inexact gradient projection method was presented,and the MIMO VLC channel capacity can be achieve in all SNR region.

・ Since the proposed MIMO VLC channel capacity is not in closed-form,we further derive both upper and lower bounds in closed-form expressions.Specifically,for discrete inputs,we derive both upper and lower bounds based on Jensen’s inequality,and then propose the optimal probability-Frank-Wolfe methods to calculate the corresponding optimal discrete input distributions.Besides,for continuous inputs,we also derive the achievable rate of MIMO VLC channel with the closed-form expression.

・ According to the relationship between mutual information and minimum mean square error(MMSE),we first derive the achievable rate for the arbitrary practical discrete constellation inputs.Then,we develop optimal power allocation scheme for the parallel SISO sub-channels to maximize rate of MIMO VLC systems by the modified water-filling method utilizing.Though numerical simulations,for the lower order modulation,the proposed power allocation scheme can bring higher rate than the equal power allocation.

The rest of this paper is organized as follows.In Section II,the MIMO VLC system model is presented.In Section III,we derive the channel capacity.Then,in Section IV,both the upper and lower bounds of the channel capacity are provided.In Section V,we discuss the optimal power allocation scheme.The simulation results are given in Section VI.Finally,Section VII concludes the paper.

Notations: (·)Tand||·||indicate transpose,Frobenius norm,respectively.E[·] indicates expectation.∇ϕ(x) represents the gradient ofϕwith respect tox.N≜ {1,2,...,N},NT≜ {1,2,...,NT},NR≜ {1,2,...,NR},Ki≜ {1,2,...,Ki},i ∈NT.

II.SYSTEM MODEL

Consider a typical IM/DD MIMO VLC channel,where the transmitter is equipped withNT >1 LEDs and the receiver withNR >1 photo-detectors(PDs),whereNT ≥NR.Let x=[x1,...,xNT]T ∈RNTdenote transmitted signal vector of MIMO VLC channel.By adopting the IM/DD scheme,the elements of the transmitted signal vector x are real and non-negative.In order to protect human eyes,both the peak and average optical power of x should be limited,i.e.,

whereAdenotes the peak power for each LED,andµdenotes the maximum average optical power.Moreover,for practical electrical circuits considerations,the electrical power of x is also constrained,i.e.,

whereεdenotes the maximum electric power of transmitter.

At the receiver side,the received signal vector y=[y1,...,yNR]T ∈RNRis given as

where H∈RNR×NTdenotes VLC channel matrix,and z∈RNRis the independent Gaussian noise with zero mean vector and varianceσ2INR.

By SVD,the channel matrix H can be expressed as H=UΛVT,where U∈RNR×NRand V∈RNT×NTare unitary matrices,the firstNcolumns of Λ are diagonal matrix,and the rest elements of Λ are 0,i.e.,Λ=[diag{λ1,···,λN},0NR,NT −N]∈RNR×NT,λ1,···,λNis the singular value of matrix H,rank(H)=N ≤NR.Both sides of Eq.(4)Multiplied by the matrix UT,we obtain the equivalent MIMO VLC channel,i.e.,

Thus,the MIMO VLC channel can be decomposed intoNparallel SISO sub-channels,and wheni > N,the equivalent input signal is inactive.

Besides,due to the unitary matrix V,the element of transmitted signal x can be expressed as

where vj=[vj,1,...,vj,NT]T,j ∈NTis thejth column vector of VT.Thus,the peak power,optical power and electrical power constraints of the MIMO VLC can be equivalently respectively reformulated as

According to constraint(8a),the amplitude of input signal of thei-th subchannelis bounded,and thus channel capacity achieving distribution ofis discrete [8].LetF() denote the discrete distribution ofwithKinon-negative mass points {}1≤k≤Ki.Without generality loss,we can assume=0,N

Then,the capacity of thei-th sub-channelCiis defined as the maximum mutual information between the input and output of the channel over all possible input distributions[27],which is given by

wheredenotes the probability density function(PDF) of.Since the noisefollows the Gaussian distribution,the PDFcan be written as [11]

By substituting Eq.(11)into Eq.(10d),the capacity of thei-th subchannelCiis given as

Due to the independence of the subchannel,the MIMO VLC channel capacityCMIMOis the sum capacity ofNsub-channels,which can be given by

III.CHANNEL CAPACITY ACHIEVING DISTRIBUTION

Based on the expression (12),the capacity of the MIMO VLC channel can be achieved by optimizing the discrete distribution of the inputs,which can be mathematically formulated as problem(13).Note that problem(13)is a non-convex mixed integer programming problem,which is difficult to handle.Moreover,the objective function(13)is non-integrable.To tackle problem(13)efficiently,we first rewrite it to a concise form.

Define

where 1Kiis aKi×1 vector with all elements equaling to 1.Then,problem (13) can be equivalently reformulated as

The mixed integer programming problem (15) is non-convex with respect to the number of discrete pointsKiand the positionsHowever,whenKandare fixed,the functionφi(pi) is convex over the probability vector pidue to the convex functiontlog2(t).Thus,we solve problem (15) iteratively,where the parametersKiandare fixed in each iteration,i.e.selecting theKivalues{}1≤k≤Kiwith equal spacing between 0 andA.For each iteration,problem(15)is convex,which can be efficiently solved by the gradient projection method.Specifically,let∇ϕi(pi) denote the gradient ofϕi(pi),which is given by

However,neitherϕi(pi)nor∇ϕi(pi)is integrable,i.e.,there is no analytic expression.To overcome this issue,the numerical integration method can be applied to approximate them,which is equivalent to the integration on the finite intervals,i.e.,[−τ1,A+τ1] and[−τ2,A+τ2],τ1,τ2>0.More specifically,the functionϕi(pi) and its gradient∇ϕi(pi) can be respectively approximated as

Based on approximated functions(pi) and(pi),we proposed an in inexact gradient projection method to solve problem (15),which is summarized in Algorithm 1.Specifically,for thei-th parallel sub-channel,let pi,ndenote then-th iteration feasible point(n=1,2,...),and pi,0denote a feasible starting point.The iteration between pi,nand pi,n−1is given by

whereαi,n >0 denotes the step size of then-th iteration,

In order to ensure a sufficient decrease,the step sizeαi,nis calculated by the backtracking line search algorithm[11],which is listed in Algorithm 2.Though Algorithm 1 and 2,the channel capacity achieving distribution can be obtained.Then,the channel capacity of MIMO VLC system can be derived by substituting the distribution into Eq.(12).

IV.UPPER AND LOWER BOUNDS OF ACHIEVABLE RATE

The obtained capacity from Algorithm 1 and 2 is not in closed-form,which limits practical MIMO VLC system design and performance analysis.Thus,we further investigate both upper and lower bounds with the closed-form expressions to approximate the capacity of MIMO VLC channels.

4.1 Upper Bound with Discrete Inputs

Based on the discrete inputs distribution in Eq.(9),the capacity of theith sub-channelCican be rewritten as Eq.(20e),where

Algorithm 1.Inexact gradient projection method.Input: set c2,c3 ≥0, nmax as stopping parameters,i=1,Ki ≥2,ωi,Ki ≤−c3;1: for i=1:NT do 2: choose a starting point pi,0 ∈Υi,and set n=0;3: repeat 4:repeat 5:computeimages/BZ_138_572_831_591_877.pngimages/BZ_138_591_819_617_865.pngϕi(pi,n)and ∇images/BZ_138_875_819_900_865.pngϕi(pi,n);6:compute the step size αi,n by Algorithm 2;7:pi,n+1=ProiΥi(pi,n −αi,n∇images/BZ_138_1010_993_1035_1039.pngϕi(pi,n));8:n=n+1;9:until ||pi,n −pi,n−1||≤c2 10:ωi,Ki=images/BZ_138_516_1238_536_1284.pngimages/BZ_138_536_1226_562_1271.pngϕi(pi,n);11:Ki=Ki+1;12: until|ωi,Ki −ωi,Ki−1|≤c3 13: popti=pi,n,Kopt i=Ki;14: end for Output: popti,Kopt i ;

Algorithm 2.Backtracking line search.Input: Initial step size ¯αi,set ρ ∈(0,1)as parameter to adjust the step size,c1 ∈(0,1),i=1;1: whileimages/BZ_138_474_1837_499_1883.pngϕi(pi,n)>images/BZ_138_916_1837_941_1883.pngϕi(pi,n−1)+c1¯αi∇images/BZ_138_418_1895_443_1941.pngϕi(pi,n−1)T (pi,n −pi,n−1)do 2: pi,n=Pr oiΥi images/BZ_138_608_1926_629_1972.png pi,n−1 −¯αi∇images/BZ_138_890_1965_916_2011.pngϕi(pi,n−1)i;3:¯αi ←ρ¯αi;4: end while Output: αi,n=¯αi;

Based the closed-form upper bound,we further study the rate maximization of VLC MIMO,which can be mathematically formulated as

Note that problem (23) is a non-convex problem,where the objective function is non-convex over the probability{pi,k}k=1,...,Ki,while the constraints are convex over{pi,k}k=1,...,Ki.To solve the problem(23),we first reformulate it as a concise form.Specifically,let us define

Algorithm 3.Probability-Frank-Wolfe method.Input: set c4 > 0 as the stopping parameter,choose a feasible starting point pi,0 ∈Υi,i ∈N,n=0;1: repeat 2: solve problem (27) to obtain optimal solution p∗i,n;3: gradient descent direction: di,n=p∗i,n −pi,n;4: solve problem min Nimages/BZ_138_1822_773_1870_818.png (ψi(pi,n+αndi,n)),obtain the step size α∗n;5: next iteration point: pi,n+1=pi,n+α∗ndi,n;6: n=n+1;7: until 0≤αn≤1 i=1‖‖‖>c4 Output: αi,n=α∗n;‖‖‖∇ψi(pi,n−1)Tdi,n−1

Together with the definitions(14a),(14b),(14c)and(14f),problem(23)can be equivalently rewritten as

To handle the non-convex objective function,the first order Taylor expansion in the pointof Eq.(24c)is given as

Therefore,problem(25)can be approximated as

Problem (27) is linear over the probability{pi,k}k=1,...,Ki,and we propose a probability-Frank-Wolfe method to obtain the corresponding optimal discrete input distribution,which is listed in Algorithm 3.

4.2 Lower Bound with Discrete Inputs

Since log(x)is a concave function with respect tox,the lower bound of the capacity of theith sub-channelCiis given as Eq.(28b),where the inequality (28a)holds based on Jensen’s inequality.Thus,the lower bound of MIMO VLC channel capacity is give by Eq.(29).

Furthermore,we investigate optimal discrete input distribution based on the lower bound(29),which can be mathematically formulated as problem(30).

Problem (30) is non-convex.By applying the first order Taylor expansion,problem (30) can be efficiently solve by the probaility-Frank-Wolfe method,and obtain the corresponding discrete inputs distribution as similar to Algorithm 3,where the details are omitted.

4.3 Lower Bound with Continuous Inputs

Note that the discrete input for the above lower bound is solved by iteration Algorithm 3 rather than the closed-form,which may bring the high computational complexity.To overcome the challenge,we next investigate lower bound with closed-form expression of MIMO VLC system based on continuous distributed inputs as the achievable rate.Specifically,letfx(x)denote the probability density function (PDF) of the continuous input vector x,andfx(x) satisfies the peak power,optical power and electrical power constraints of the MIMO VLC system as follows

whereS1∈RNTisNTdimensional real space and all elements are limited to [0,A],i.e.,S1={x|0≤xj ≤A,∀j ∈NT,xj ∈x}.

Thus,MIMO VLC channel capacity with continuous inputs is given as

According to Eq.(32d),the lower bound can be obtained by maximizing differential entropyh(x).Based on the definition of differential entropy

the differential entropy maximization problem can be mathematically formulated as

where 1NTis a vector with all elements are 1.

Note that problem (34) is convex overfx(x).Therefore,by placing the constraints into the Lagrangian function of problem(34)yields

whereα,βandγare the Lagrange multipliers corresponding to constraints(34b),(34c)and(34d),respectively.

Let the first derivation of Eq.(35) with respect tofx(x)equal to 0,

According to equation (36),we obtain the optimal continuous distributionfx(x)as

Then,by substituting Eq.(37) into constraints Eq.(34b),Eq.(34c) and Eq.(34d),parametersα,βandγare solutions of the following equations.

Therefore,by substituting Eq.(37) into Eq.(32d),we obtain the lower bound of MIMO VLC channel capacity with continuous inputs as follows

V.OPTIMALPOWERALLOCATION WITH ARBITRARY DISCRETE INPUTS

In this section,we further investigate a general power allocation scheme for MIMO VLC system with arbitrary discrete inputs.Specifically,let s=[s1,...,sN]Tdenote the input vector,andsiis drawn from discrete constellations set{si,k}.The transmitted signal x is given as

By substituting Eq.(40) into Eq.(4) and applying SVD,thei-th channel of equivalent received signal Eq.(6)can be re-expressed as

The peak power,average optical power and electrical power constraints forsi,kare respectively given as

wheresi,kis thek-th constellation point andpi,kis the corresponding probability,Porepresents the total average optical power,Perepresents the total electrical power restraint.

The achievable rate fori-th sub-channel can be written as

wheredenotes the PDF of.

Then,the achievable rate for thei-th sub-channel is given by Eq.(45b),where=si,k −si,m.

Therefore,the achievable rate of MIMO VLC system can be expressed as

With any given inputs discrete distribution,the optimal power allocation problem can be mathematically formulated as

The constraints of problem (47) are convex forqi.Since log(exp(x)) is convex and non-decreasing with respect tox,andx(t)=−is convex with respect tot,log(exp(x(t))) is convex with respect totbased on convex preserving operation.Thus,the objective function of problem (47) is concave forqi.

To achieve the optimal power allocation schemeqi,the Lagrangian function of problem(47)is given by

whereGi=ω1τ2i+.

According to[29],the relationship between mutual information and MMSE is given by

where MMSEi(SNR)=is the MMSE ofandis the conditional expectation ofsi.

Although there is no closed-form expression for MMSEi,we can get the upper bound of MMSEi[30].

whereδ2siis the variance ofsi.

Thus,the differential function ofRican be written as

By substituting Eq.(54)into Eq.(50a),we obtain

Therefore,the expression of power allocation parameterqiis given as

Thus,the optimal power allocation of problem(47)is given as

In summary,the proposed optimal power allocation scheme with arbitrary discrete inputs,is presented in Algorithm 4.

Algorithm 4.Optimal power allocation with arbitrary discrete inputs.Input: set ω1 ∈[ωmin,ωmax], ωmin=0,set c5 > 0 as the stopping parameter;1: while ωmax −ωmin >c5 do 2: set ω1=1/2(ωmin+ωmax);3: substitute Eq.(56)into Eq.(50e),find minimum ω2 ≥0 that satisfied Eq.(50e);4: if Gi ≤λ2i σ2 then 5:substitute ω1,ω2 for Eq.(56),get q∗i;

6: else 7:q∗i=0;8: end if 9: if q∗i statisfies the i nequality(50d)then 10:set ωmax=ω1;11: else 12:ωmin=ω1;13: end if 14: end while Output: αi,n=¯αi;

VI.SIMULATION RESULTS AND DISCUSSIONS

In this section,we present the simulation results of the proposed channel capacity calculated methods and power allocation scheme for MIMO VLC system.Assume that the MIMO VLC system is equipped with two LEDs and two PDs,i.e.,NT=2,andNR=2,and the peak optical powerA=1.The VLC channel matrix H is given as

After SVD,we can obtain the corresponding equivalent channel gain Λ=diag(Λ1,Λ2),Λ1,Λ2>0.Thus,there are two sub-channel,i.e.,the sub-channel 1 and sub-channel 2,where the channel gains are Λ1≈0.8520 and Λ2≈0.3521,respectively.

6.1 Channel Capacity

First,we evaluate the channel capacity of the MIMO VLC by using the proposed inexact gradient projection method.Figure 1 plots the channel capacity of the MIMO VLC versus SNR withκ=4 andκ=5,whereκ≜and SNR=.With the increase of SNR,channel capacity of MIMO VLC increases.In addition,we note that the channel capacity ofκ=5 is larger than that ofκ=4 in whole SNR region and the difference becomes larger as the SNR increases.Moreover,the capacity of sub-channel 1 is higher than that of sub-channel 2 because the channel gain of subchannel 2 is higher.

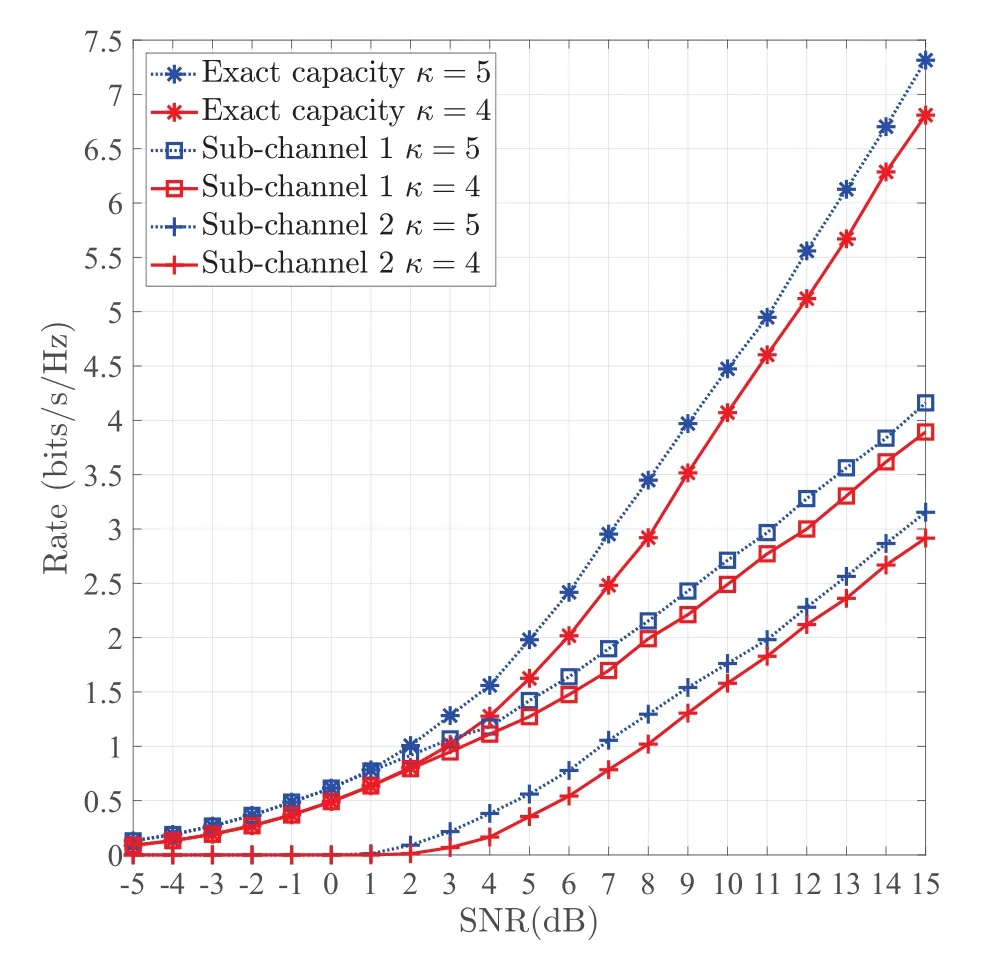
Figure 1.Exact capacity,the rate of sub-channel 1 and subchannel 2 versus SNR with κ=4,5.

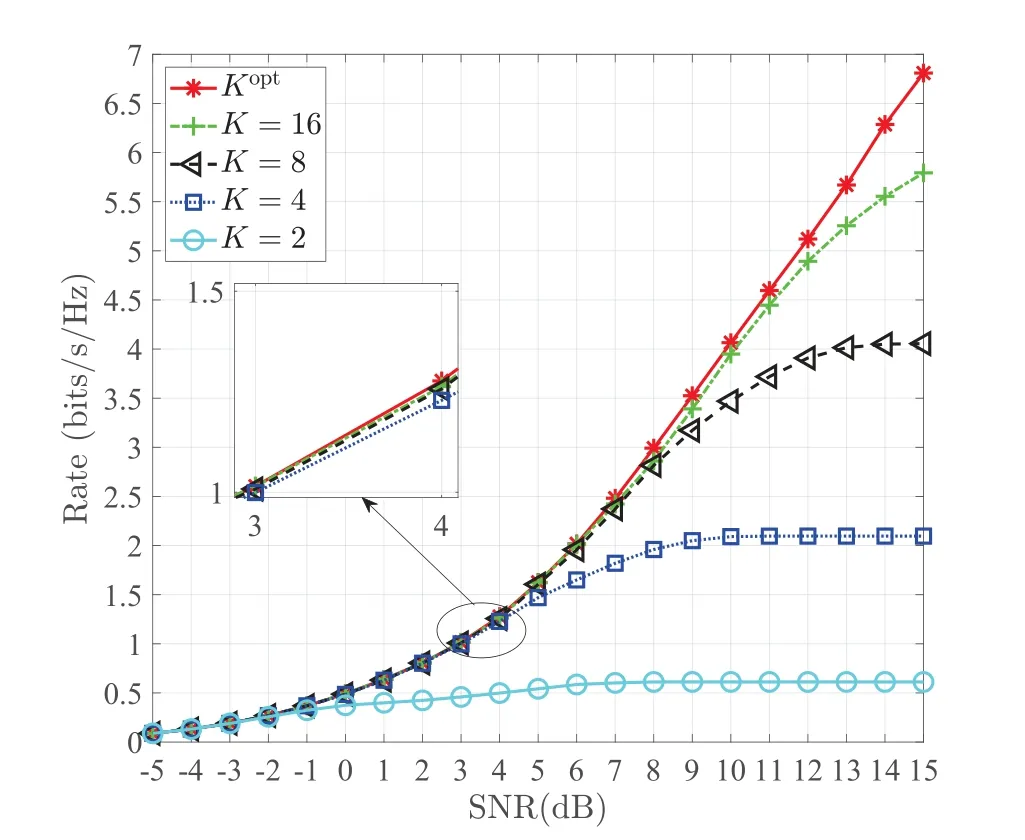
Figure 2.Exact capacity versus SNR with Kopt and K=2,4,8,16.

Figure 2 shows the capacity of the MIMO VLC versus SNR forκ=4 with different number of discrete pointsK=2,4,8,16.It is observed that for low SNRs,only two points are needed and OOK modulation is fit for low SNRs.Moreover,the capacity of the MIMO VLC rises as number of points increases for high SNRs.Therefore,we conclude that more number of discrete points are needed to achieve the channel capacity as SNR increases.In other words,as the SNR increases,the modulation order of the VLC MIMO system should also increase in order to achieve a high rate.

Figure 3 compares the channel capacity with its upper bound,lower bound with discrete inputs and the lower bound with continuous inputs of MIMO VLC.Figure 3 shows that the gaps between the channel capacity and the lower bound with discrete inputs are tight in low and high SNRs.Moreover,the lower bound with discrete inputs are higher than the lower bound with continuous inputs,which agrees with the conclusion that the discrete distribution is the optimal input distribution for VLC system[8].

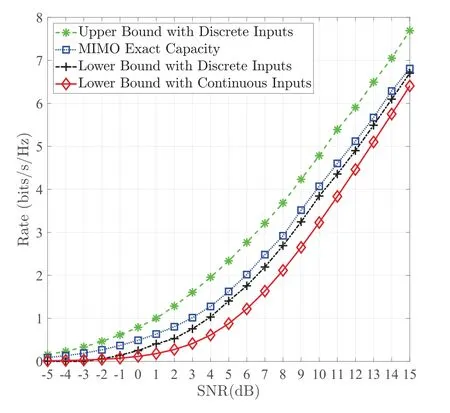
Figure 3.Comparison among exact capacity,upper and lower bound with discrete inputs,and lower bound with continuous inputs versus SNR.

Figure 4 and figure 5 illustrate the optimal positions {} and optimal input distribution{,p∗k} versus SNR for sub-channel 1 and 2,respectively.In Figure 4(a),we can observe that optimal input positions only have two discrete points when SNR≤−4(dB).With the increase of SNR,the optimal input positions have more number of discrete points and multi-pulse amplitude modulation(M-PAM)can achieve the channel capacity of MIMO VLC system.Note that the probabilities of discrete points are not equal.Figure 5 presents the similar results,however,there is no feasible distribution when SNR<2dB.Moreover,the discrete points of Figure 4(b)are more than that in Figure 5(b),because the gain of sub-channel 1 is higher than that of sub-channel 2.

6.2 Power Allocation of MIMO VLC

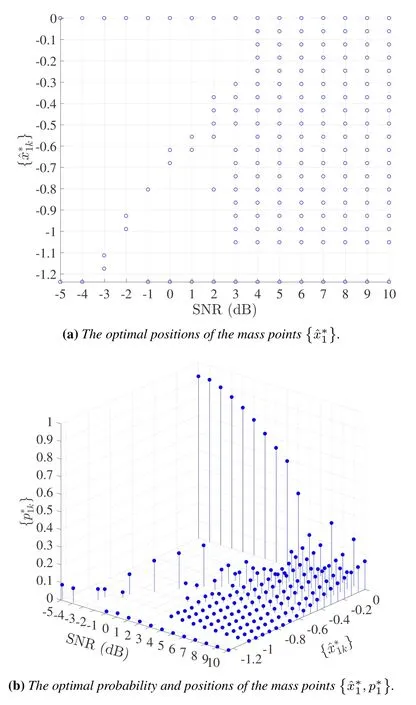
Figure 4.The optimal input distribution versus SNR for sub-channel 1.

In this part,we access the performance of the proposed power allocation scheme.The channel matrix is the same as(58).The number of the mass pointsKi,i ∈Nis set as 21.Peak optical powerAis fixed with 1,and the average optical powerPois 3.The noise powerσ2is assumed as 0.025.

Figure 6(a) illustrates the rate at SNR=0 dB versus electrical power threshold with the discrete input distributions,which are derived in Section III,Section 4.1,and Section 4.3,respectively.Moreover,the rate of the discrete input with equal power allocation is also presented for comparison.We can observe that the rate of discrete inputs based on the proposed power allocation scheme is higher than that based on the equal power allocation scheme.The rate of discrete input of the upper bound is highest,and the rate of discrete input of the lower bound is lowest.In addition,it can be seen that the rates tends into a constant in spite of increasing of electrical power threshold.This is because the source entropy is also fixed for for a given discrete input distribution.

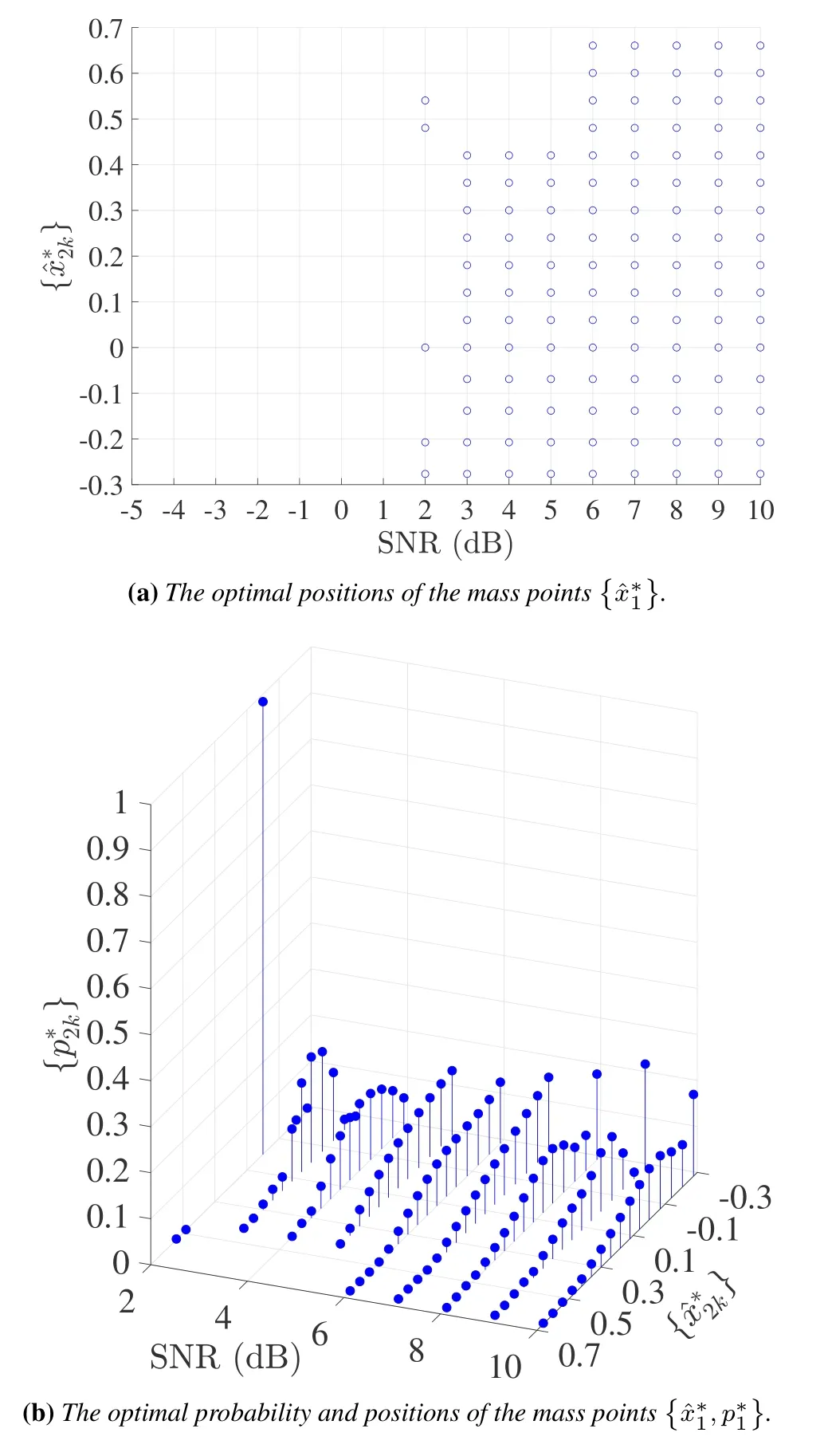
Figure 5.The optimal input distribution versus SNR for sub-channel 2.

Figure 6(b)shows the similar comparison of the rate with discrete inputs at SNR=25(dB).We can see that the rate of discrete inputs based on the proposed power allocation scheme is close to that based on the equal power allocation scheme.Comparing Figure 6(a)and(b),the proposed power distribution scheme can significantly improve the MIMO VLC rate of low-order modulations.

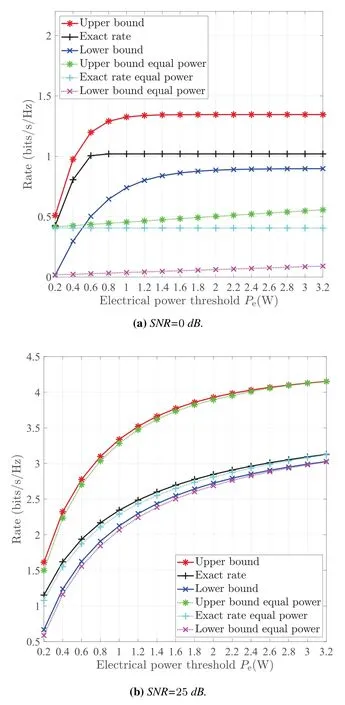
Figure 6.Rates of discrete inputs with optimal and equal power allocation versus electrical power threshold.

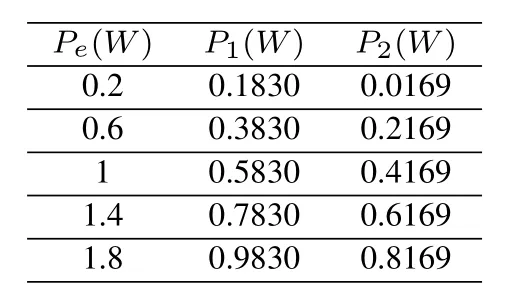
Table 1.Power allocation results of MIMO VLC system.

The power allocation results of two sub-channels of MIMO VLC are listed in Table 1,whereP1andP2are allocated power of the sub-channel 1 and 2,respectively.Table 1 shows that the allocated power of the sub-channel 1P1is higher than that of sub-channel 2P2because the gain of sub-channel 1 is more higher.Note that,the gap betweenP1andP2becomes smaller asPeincreases.Thus,equal power allocation can be used approximated the optimal power allocation for high electrical power threshold,which also be verified in Figure 6(b).

VII.CONCLUSION

In this paper,we propose an inexact gradient projection method to calculate the channel capacity of MIMO VLC systems under the peak,average optical and electrical power constraints.Moreover,both upper and lower bound of channel capacity of MIMO VLC are derived with closed-form expressions.To the best of our knowledge,the theoretical framework of channel capacity MIMO VLC with electrical power constraints is established for the first time.Furthermore,the optimal power allocation scheme is developed for arbitrary practical discrete constellation inputs.Various numerical results have been provided to illustrate the effects of the calculated channel capacity of MIMO VLC and the performance of the proposed optimal power allocation scheme.

ACKNOWLEDGEMENT

The work of Ruixin Yang was supported by the Graduate Innovation Program of China University of Mining and Technology(2022WLKXJ016);in part by the Postgraduate Research&Practice Innovation Program of Jiangsu Province (KYCX22_2549).The work of Wen Cao was supported by Shaanxi Provincial Natural Science Foundation of China (2023-JC-YB-510),the Fundamental Research Funds for the Central Universities,CHD(300102322103).This work of Linqiong Jia was supported in part by Natural Science Foundation of Jiangsu Province(BK20200488).The work of Guanjie Zhang was supported in part by Challenge Cup National Student Curricular Academic Science and Technology Works Competition(DCXM202212).