一道2022年山东省预赛试题的探究

盛 龙

安徽省桐城中学 (231400)

试题设计平凡、朴实、常规，是学生最熟悉的题型，入手比较容易且解题的思路很多.考查了直观想象、数学运算和逻辑推理等数学核心素养，检验了学生分析问题和解决问题的能力，是一道有探究性的好题.

一、解法探究

若过原点的圆x2+y2=r2满足：过圆上任意一点M的切线与椭圆C交于A,B两点，且OA⊥OB.(当切线斜率不存在时容易探究，下面只探究斜率存在的情形)

证法1：(设线)设A(x1,y1),B(x2,y2).

证法2：(设切点)设圆O在点M(x0,y0)(x0y0≠0)处的切线方程为x0x+y0y=r2，联立

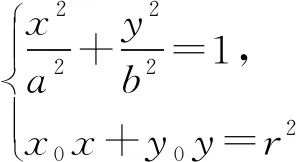
两种方法最后一步都要利用到关系式x1x2+y1y2=0，显然点A的坐标与点B的坐标是有一定的关系，能否打破解题常规的定势思维，在设点B的坐标上下功夫呢？结果是出人意料的.

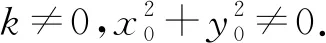
通过巧妙设元，利用简单的平面几何知识构造等式，跳出解析几何题解答常规的思维框架，“四两拨千斤”就干脆利落地得到圆的半径，大大减少了计算量和中间步骤，在解题过程中展现思维的睿智和数学的魅力.

二、背景探究——椭圆“内准圆”性质

一个好的试题，往往具有深刻的背景，上述预赛试题实质上是椭圆“内准圆”的一个基本性质.

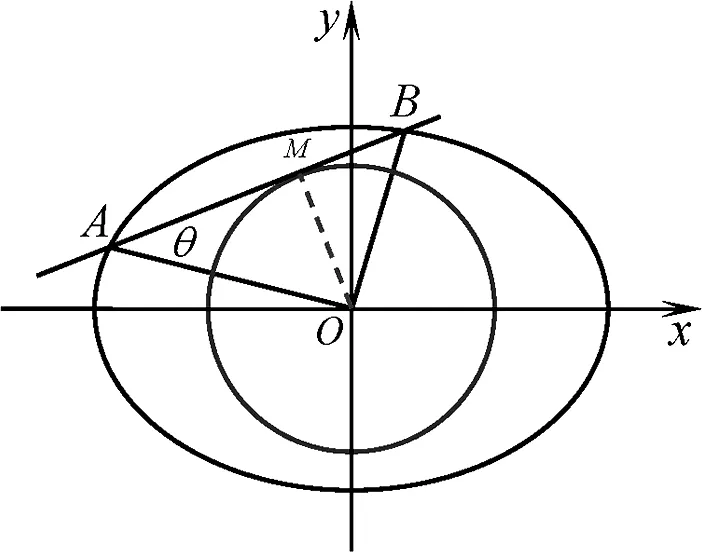
图1

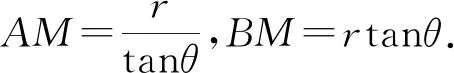
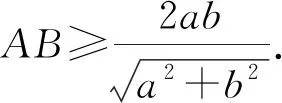
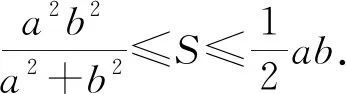
三、命题再创造

对试题的命制作一点猜测性研究，以期与命题人对话，为此设计以下题目.

(1)求椭圆C的方程；

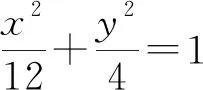
(1)求椭圆C的方程；

(2)过坐标原点的直线与椭圆交于M,N两点，过点M作圆x2+y2=2的一条切线，交椭圆于另一点P，连接PN，证明：|PM|=|PN|.

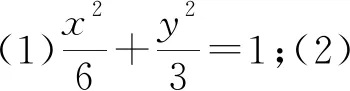
(1)求椭圆C的方程；

(2)过坐标原点的直线与椭圆C交于M,N两点，过点M作圆x2+y2=2的一条切线，交椭圆于另一点P，连接PN，求△PMN面积的最大值.

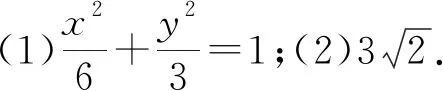
设计思路：题3的进一步深化，S△PMN=2S△OPN，性质3的特殊化.

基于以上对3到题目的设计，解析几何试题考查学生用解析几何方法解决解析几何问题的能力，使学生体会到对于几何问题，“解析化”的途径必须进行认真的研究探索和选择，同时强调运算的准确性对于解析几何是十分必要的.