例析导函数零点讨论中分界点的确定技巧

郝淑萍

甘肃省武威市凉州区职业中等专业学校 (733000)

我们在运用导数解决有关函数问题时，经常在对导函数的分类讨论中，由于不能正确划分分类标准造成解题失误.本文针对这个问题，通过分析和研判典型问题的求解，进一步探讨几种常用的确定分界点的方法，供读者朋友参考.

1.根据影响导函数正负号的参数取值确定分界点

例1 已知函数f(x)=axlnx+2x(a∈R)，试讨论f(x)的极值情况.

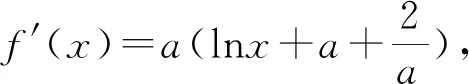
点评：求出导函数后，如果能直接看出参数是确定导函数的因素之一，应该通过讨论确定导函数的符号.此类问题是比较简单的一类分类讨论问题，通过对参数分类，就能直接确定导函数的正负号，这样原函数的单调性就随之而出了.

2.根据导函数零点的大小确定分界点

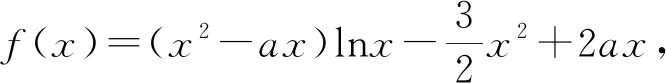
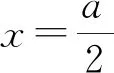
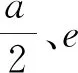
3.根据导函数零点与定义域的关系确定分界点

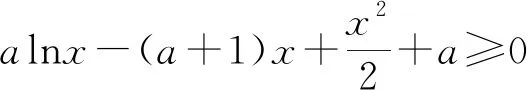
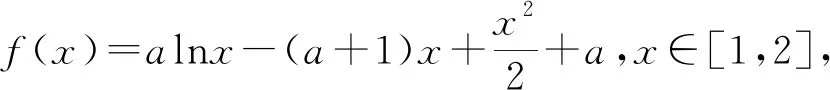
①当a≤1时，f′(x)≥0，所以函数f(x)在[1,2]上单调递增，所以f(x)max=f(2)=aln2-a≥0成立，解得a≤0，所以a≤0.

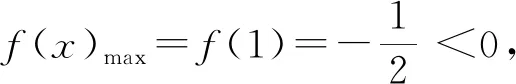
综上可得，实数a的取值范围是(-∞,0].

点评：首先需要确定导函数零点是否分布在定义域内，若不能确定，应该要分类讨论.本解法中,抓住导函数f′(x)的零点a是否在定义域[1,2]内进行讨论，非常重要,从而可确定函数在给定区间内的单调性，然后容易求出最值.

4.根据二次项系数的正负情况确定分界点

例4 已知函数f(x)=lnx+x+1-m(x2+2x).若对任意的x>0，都有f(x)≤0成立，试求整数m的最小值.

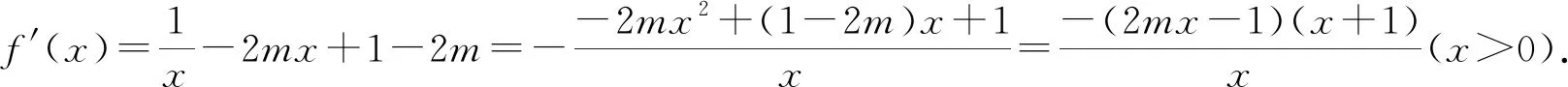
①当m≤0时，由于x>0，则2mx-1<0，x+1>0，知f′(x)>0，故f(x)在(0,+∞)上单调递增，又f(1)=ln1-m×12+(1-2m)+1=-3m+2>0，不合题意，故舍去.

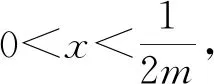
点评：如果导函数是一个关于参数的二次三项式，首先要对最高项的系数分类讨论，根据二次项系数的正、负号，判断二次函数图象的开口方向，从而可确定导函数的变号零点.

5.根据含参数的二次函数的对称轴确定分界点

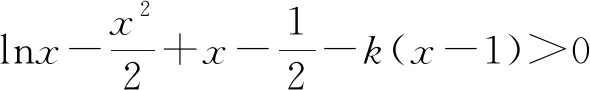
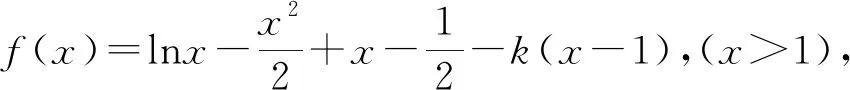
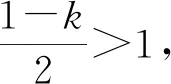
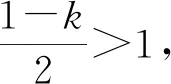
综上，实数k的取值范围为(-∞,1).

点评：在求导后，若导函数是二次函数或与二次函数有关，而此时的含参数的二次函数又无法确定零点，通过找对称轴作为分界点，进行分类讨论是常见的选择之一.

6.分离参数时，根据参数的系数取值情况确定分界点

例6 若不等式x2-mx+1+ex+2≥0恒成立，求实数m的取值范围.

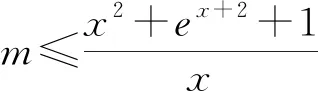
点评：在一些求参数范围问题时，常可以采取分离参数的方法，将问题转化为另一个函数求最值问题，而在分离时需要通过分类讨论才能达到目的.

分类讨论是一个重要的数学思想方法，这也是高考试卷中经常出现的题型，具有很强的区分度，如果能比较有效的掌握一类问题的分类解决，就可能得到一个满意的成绩，也可能使人生上升到一个新的成长平台，故而不可言轻易放弃.