基于RGPI观测器的四旋翼无人机抗风扰控制

仇家鑫，孙振兴

(南京工业大学电气工程与控制科学学院，江苏 南京 211816)

1 引言

近年来，以四旋翼为代表的无人机技术迅速发展。由于四旋翼具有结构简单、转向灵活、垂直起落、定点悬停等特点，它的应用十分广泛。在军事领域，四旋翼可以被用来侦查、攻击和执行救援任务[1]。在商业领域，四旋翼有望取代骑手配送外卖[2]和快递[3]，解决外卖带来的交通问题，并极大地缩短配送时间。在民用领域，搭载喷洒设备的四旋翼可以用于喷洒农药[4，5]，显著提高农业生产效率。

为了满足这些应用需求，四旋翼的控制系统必须具有足够好的控制性能。事实上，四旋翼无人机是通过四个控制输入来控制六个自由度的典型欠驱动系统，同时也是一个多变量、强耦合的系统[6]。此外，它对外界参数变化十分敏感，具有高度非线性[7]。因此，研究高性能、安全可靠的四旋翼无人机控制算法，对于确保其稳定飞行、增强系统的鲁棒性与抗扰动性，具有重要的理论与实际应用价值。

传统的四旋翼控制器在位置环和姿态环使用串级比例积分微分(PID)控制器[8]，但是PID控制器有响应迟滞、对突变敏感、抗扰动能力差等缺点[9]，不易满足高性能要求。随着现代控制理论的发展，许多先进的控制策略已经被应用到四旋翼上。文献[10]将四旋翼的姿态控制分为3个独立的通道分别设计了反步控制器，具有超调量小与响应速度快等优点，但该方法忽略了各通道间耦合的影响，且未考虑外部干扰的影响；文献[11]先对四旋翼的动力学模型进行线性化，然后对线性模型设计了改进的LQR控制器，显著提高了瞬态响应速度，但是LQR需要精确的数学模型，而四旋翼无人机无法建立精确的数学模型[12]。这些方法在一定程度上优化了四旋翼无人机的性能，但没有考虑扰动对系统影响。

然而，在实际应用场景中，四旋翼不可避免地受到各种扰动，特别是风扰。室外飞行的四旋翼无人机在受到阵风时，会产生桨叶挥舞现象[13]。桨叶挥舞会导致螺旋桨攻角发生变化，影响螺旋桨的升力系数和转矩系数，从而导致螺旋桨升力和转矩发生剧烈变化[14]。另外阵风作用在机体上会形成额外的力矩，极大地影响四旋翼无人机的稳定性。因此，在控制器设计中考虑风扰等扰动，提高抗扰动能力，对于优化四旋翼无人机的性能具有重要意义。在实际系统中，大多数扰动无法直接测量，而且额外的传感器会增加成本。常见的方法是采用扰动观测技术，并将扰动观测值通过前馈环节进行补偿。文献[15]采用未知输入观测器(UIO)，对未知的扰动进行估计，提高了系统的响应速度；文献[16]引入扩张状态观测器(ESO)对未知扰动进行估计，并结合反步法设计控制器进行补偿，实现了对扰动的抑制，但是ESO难以精确估计快速变化的扰动；文献[17]设计了基于高阶滑模观测器的全状态内环控制器，在受到随机扰动的情况下，系统能够保持一定的稳定性，但是高阶滑模观测器会产生震荡，影响系统的控制精度。通常情况下，由阵风、耦合等因素引起的扰动可以用时间序列多项式表示。而对于这类时变扰动，广义比例积分观测器(General proportional integral observer，GPIO)能够提供更高的估计精度[18]。

因此，针对四旋翼姿态的抗风扰控制问题，本文提出了一个基于串级PID和降阶GPI观测器的复合控制策略。其中，反馈部分采用比例控制器。前馈部分采用了降阶GPI观测器。该复合控制策略有效提高了四旋翼无人机的抗风扰能力。

在本文第二部分详细描述了四旋翼的数学模型。第三部分和第四部分给出了复合控制器设计和稳定性分析。第五部分给出了实验结果，验证了该复合控制策略的抗风扰能力。最后，第六部分给出了结论。

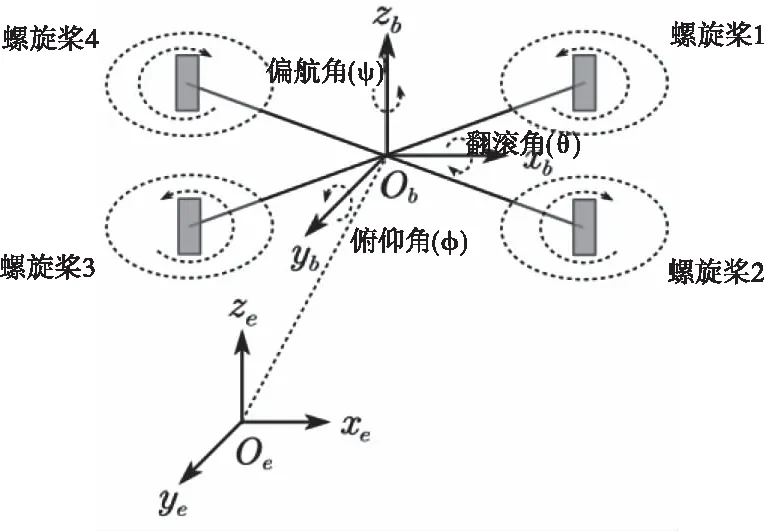
图1 四旋翼无人机系统示意图

2 四旋翼无人机的数学模型

为了建立四旋翼无人机的动力学模型，必须定义两个坐标系。如图1所示，第一个坐标系是固定在地面上的基坐标系E：{Oe，xe，ye，ze}。第二个坐标系是机体坐标系B：{Ob，xb，yb，zb}，其原点与四旋翼的中心重合。四旋翼系统的数学模型基于以下假设[19]：

假设1：四旋翼是一个刚体，其几何中心与重心重合。

假设2：四旋翼的质量和惯性矩是恒定的。

假设3：四旋翼垂直于重力方向Oeze轴，螺旋桨垂直于Obzb轴。

假设4：四旋翼为X形结构。标号为偶数的螺旋桨顺时针旋转，而标号为奇数的螺旋桨逆时针旋转。

根据四旋翼无人机系统的示意图，可以通过以下公式计算出四旋翼的转矩

(1)

这里Ti(i=1，2，3，4)是第i个电机在空气中产生的推力，τ=[τx，τy，τz]T是转矩，l是旋转中心到每个电机的距离，b是螺旋桨力矩与推力的比值一个常数。

根据欧拉方程，转矩和角加速度之间的关系由下式给出

(2)

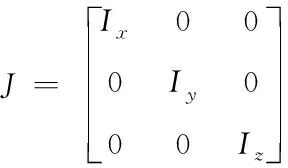
(3)

其中，Ix，Iy和Iz是沿方向x，y和z的惯性矩。

观察方程(2)，可以看到系统通道之间存在强耦合。为了降低系统的控制难度，可以将耦合部分、系统干扰和不确定参数视为总干扰。因此，可以得到

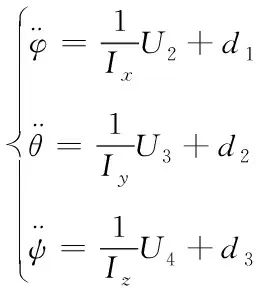
(4)

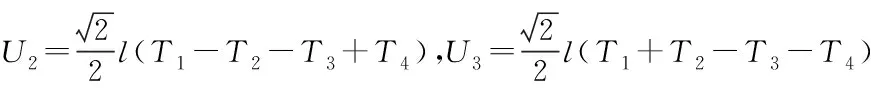
定义

(5)

四旋翼无人机的状态空间模型由下式给出

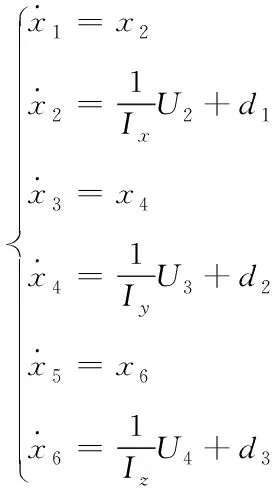
(6)

3 控制策略

结合上述模型与实际应用，总扰动主要是由耦合扰动和外部扰动引起的。为了提高系统的抗风扰能力，设计了一个复合控制器。

3.1 降阶广义比例积分观测器设计

对于状态空间方程F

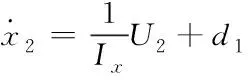
(7)

可以将其扩展如下

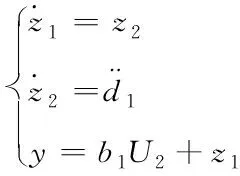
(8)

根据系统(8)，可设计降阶GPI观测器如下

(9)

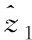
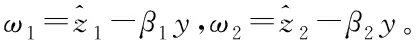
(10)

3.2 复合控制器设计

为了简化四旋翼无人机姿态的控制难度，控制器分为角度控制器和角速度控制器。角度控制器和速度控制器采用比例控制器。控制器结构如图2所示。

角度控制器如下

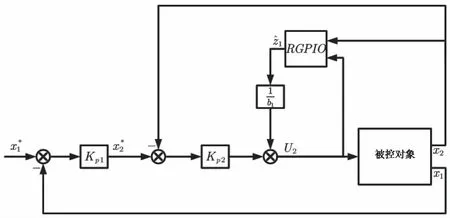
图2 复合控制器结构图

(11)

角速度控制器如下

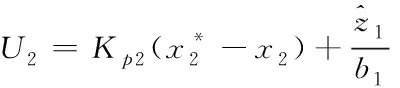
(12)

其中，Kp2是角速度控制器的比例增益。

4 稳定性分析

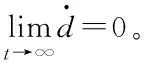
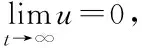
(13)

(14)

将(13)式与(14)式联立，可得闭环系统方程如下

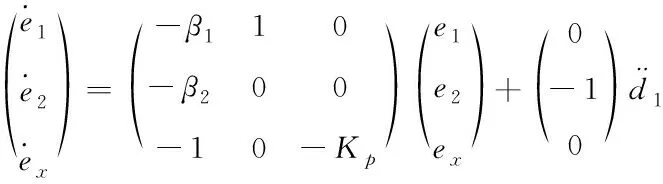
(15)

(16)

因此，在稳态下所提的控制方法完全消除了扰动造成的影响。

5 实验结果分析

5.1 实验平台

为了验证本文提出的复合控制器的性能，对所提算法进行了实验验证，四旋翼实验平台如图3所示的。整个平台分为：机械部分、电气部分和控制器部分。

1) 机械部分

图3 四旋翼无人机实验平台

四旋翼机体结构采用尼龙和玻璃纤维，具有重量轻，硬度高的特点。为了提供足够的动力，选择了AIR2216-kV880无刷电机和T1045螺旋桨。此外，控制板与机架的连接部分用橡胶圈减震。四旋翼的模型参数在表1中给出。

2) 电气部分

控制板由控制器STM32F407、3轴加速度计和3轴陀螺仪BMI088、3轴磁力计AK8975和气压计SPL06组成。传感器均通过SPI总线连接到控制器，实现更高速的数据传输。此外，为解决传感器的温漂问题，控制板上设计了恒温电路。

3) 控制器部分

控制器软件主要包括姿态解算和控制器。姿态解算使用Mahony算法和互补滤波算法对陀螺仪，加速器和磁力计的数据进行融合，精度可达0.1度。而控制器是专为测试算法而设计。

表1 四旋翼无人机的模型参数

5.2 结果分析

为了验证本文提出的复合控制器的抗风扰性能，设计了两组比较实验，将复合控制器与传统的PID控制器进行比较。第一组是无风扰条件下控制系统跟踪性能试验，给定翻滚角、俯仰角、偏航角设定值，即幅值为18°、频率为0.2Hz的正弦波，根据控制系统的跟踪误差与稳态误差来判断控制器的性能。第二组是风扰条件下控制系统跟踪性能试验，在第一个试验基础上，使用位置变化的电风扇引入时变扰动，根据跟踪轨迹的平滑程度和稳态误差判断风扰下控制器的抗扰动性能。

5.2.1 无风扰条件下控制系统跟踪性能试验

在无风扰条件下，翻滚角、俯仰角、偏航角跟踪幅值为18°、频率为0.2Hz的正弦波。分别使用本文提出的复合控制器和PID控制器进行试验。PID控制器跟踪效果如图4和图5所示，复合控制器跟踪效果如图6和图7所示。

将图5与图7对比可以看出，复合控制器控制下的最大跟踪误差的绝对值与PID控制器的相差约5倍，而复合控制器的稳态误差与PID控制器的相差了一个数量级。此外从图4(a1)、图4(b1)、图6(a1)和图6(b1)可知，复合控制器的跟踪曲线与设定值曲线基本重合，而PID控制器的跟踪曲线出现明显的跟踪误差。此外从图4(a2)、图4(b2)、图6(a2)和图6(b2)可以看出，PID控制器下的角速度跟踪曲线也有较大的跟踪误差和滞后，而复合控制器的角速度跟踪曲线与目标值几乎重合。因此，相比于传统的PID控制器，本文提出复合控制器在无干扰条件下具有更高的跟踪速度和稳态精度。

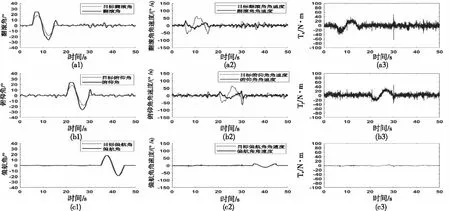
图4 无风扰下PID控制器角度跟踪曲线、角速度跟踪曲线和力矩曲线

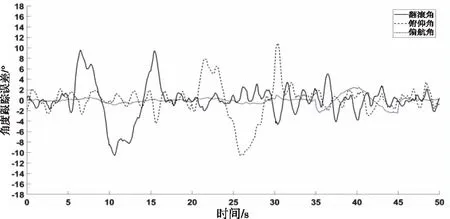
图5 无风扰下PID控制器角度跟踪误差曲线

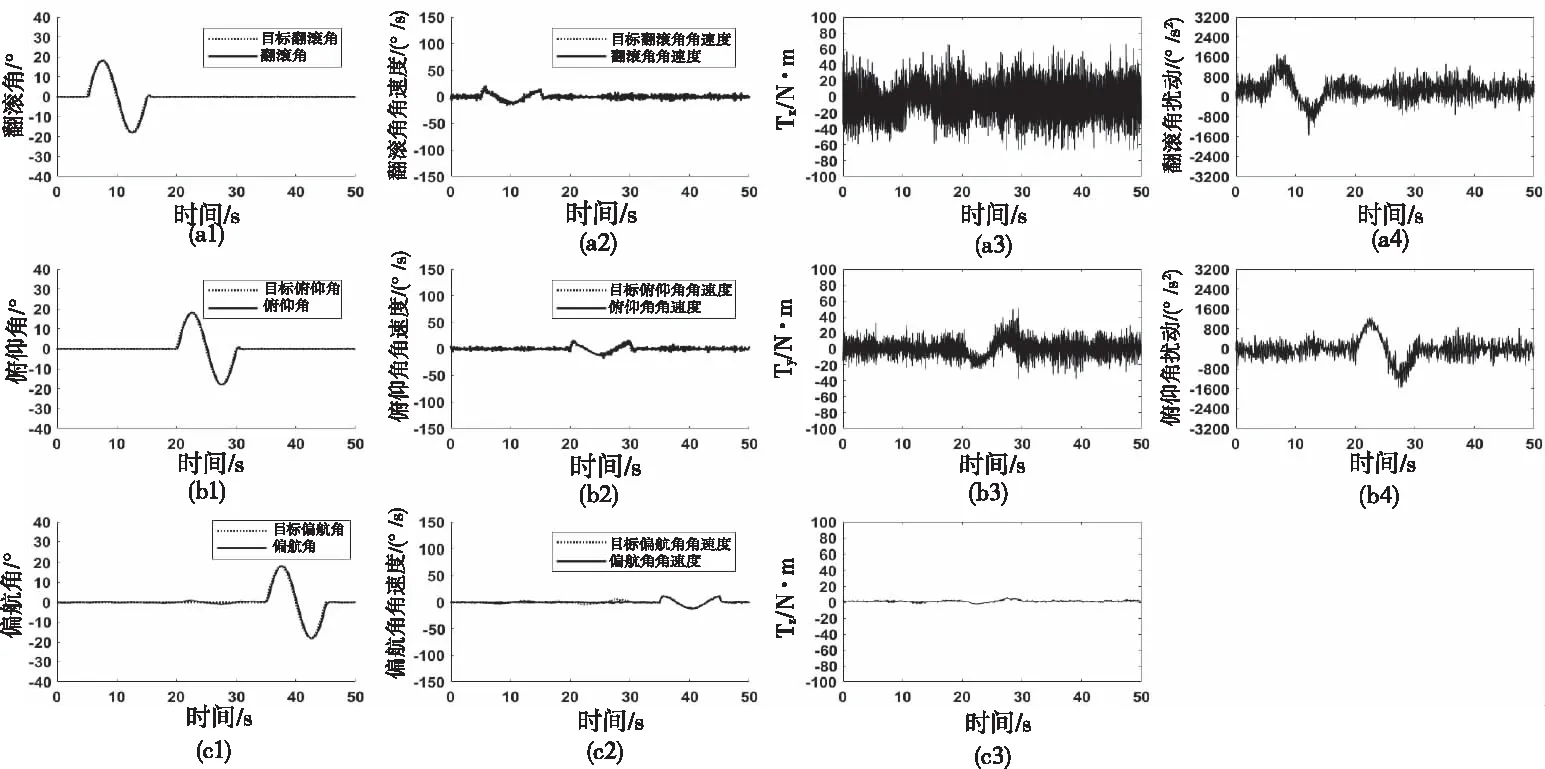
图6 无风扰下复合控制器角度跟踪曲线、角速度跟踪曲线、力矩曲线和扰动估计曲线

5.2.2 风扰条件下控制系统跟踪性能试验

图7 无风扰下复合控制器角度跟踪误差曲线

在无干扰跟踪实验的基础上，用位置快速变化的电风扇模拟四旋翼飞行过程中受到的风扰，以此来验证控制器在风扰下的抗扰动性能。PID控制器跟踪效果如图8和图9所示，复合控制器跟踪效果如图10和图11所示。

从图8(a1)、图8(b1)、图8(c1)和图9中可以看出，在角度设定值为0的时间段内，PID控制器控制下的翻滚角、俯仰角和偏航角的波动范围分别为-9.2°～9.0°、-9.7°～10.4°和-1.0°～1.4°，在跟踪正弦信号时，PID控制器控制下的翻滚角、俯仰角和偏航角的最大跟踪误差的绝对值分别为13.9°、14.4°和3.0°。从图10(a1)、图10(b1)、图10(c1)和图11中可以看出，在角度设定值为0的时间段内，复合控制器控制下的翻滚角、俯仰角和偏航角的波动范围分别为-0.2°～0.3°、-0.3°～0.4°和-0.3°～0.4°，在跟踪正弦信号时，复合控制器控制下的翻滚角、俯仰角和偏航角的最大跟踪误差的绝对值分别为2.7°、3.0°和2.4°。复合控制器控制下的姿态角稳态误差与跟踪误差与PID控制器控制下的相差几乎10倍。此外，综合图8、图9、图10、图11可以看出，PID控制器控制下的翻滚角和俯仰角出现明显的大幅度振荡，而复合控制器控制下的翻滚角和俯仰角的跟踪曲线依然十分平滑。因此，在风扰条件下，复合控制器的跟踪轨迹受到的影响非常小，能够快速稳定的跟踪给定信号，而传统串级PID控制器则出现明显的振荡，说明复合控制器能够提高四旋翼的抗风扰能力。

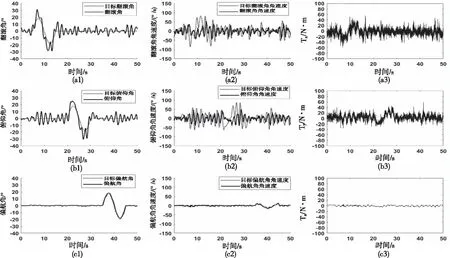
图8 风扰下串级PID控制器角度跟踪曲线、角速度跟踪曲线和力矩曲线

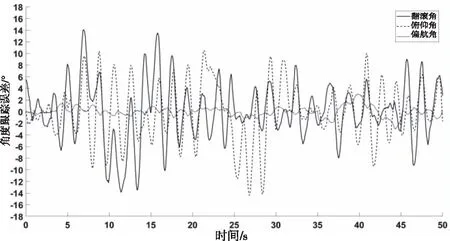
图9 风扰下串级PID控制器角度跟踪误差曲线

图10 风扰下复合控制器角度跟踪曲线、角速度跟踪曲线、力矩曲线和扰动估计曲线

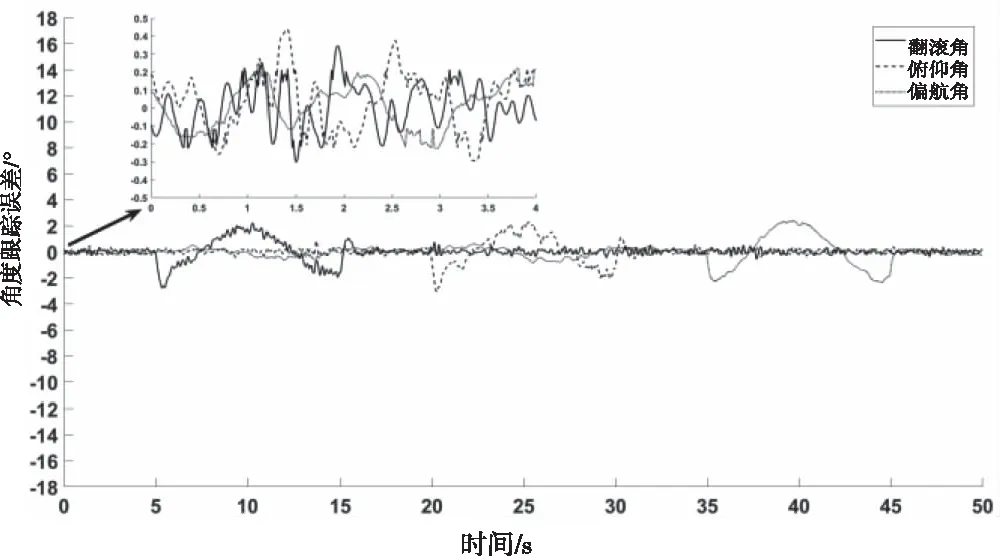
图11 风扰下复合控制器角度跟踪误差曲线

5.3 实验结果分析

通过两组比较实验可以得出，本文设计的复合控制器在无风扰条件下，四旋翼姿态的稳态精度和跟踪速度明显优于PID控制器。此外，在风扰条件下，PID控制器出现明显的大幅度振荡，而复合控制器依然能够平滑的跟踪目标信号，即对风扰具有较强的抑制能力。综上所述，本文提出的复合控制器具有稳态精度高、响应速度快、抗风扰能力强等特点。

6 结论

本文提出了一种基于降阶GPI观测器的四旋翼无人机抗风扰控制方法，用来提高四旋翼的抗风扰性能。首先，设计了降阶GPI观测器，用来观测时变扰动，并通过前馈环节补偿扰动。其次，设计了由比例控制器和降阶GPI观测器组成的复合控制器。实验结果表明，本文所提出的四旋翼抗扰动控制策略能够有效地提高四旋翼的抗风扰能力，并具有较高的稳态精度和响应速度。