基于熵权-灰色层次分析的MSaaS可信度评估

蒋海峰，任学文，梅 铮，徐 筠

(1. 南京理工大学自动化学院，江苏 南京 210094；2. 北京仿真中心航天系统仿真重点实验室，北京 100854)

1 引言

2015年，北约提出基于云计算的的建模仿真即服务(MSaaS)，为仿真应用的快速构建提供了新思路。MSaaS可信是基于仿真系统对实际世界复杂对象或系统实现正确的观、分析与控制的保证[1]。

目前，国内外的学者对MSaaS的研究主要集中在基于MSaaS的并行和分布式仿真、基于MSaaS的建模方法等理论方法上[2-4]，而可信计算的研究主要集中在计算机软硬件层面，缺少仿真服务所需要的一些特殊属性，较难适应仿真服务可信评估需求。因而，如何建立一个MSaaS仿真系统的综合可信度评估指标体系，如何对该系统可信程度进行有效评估是亟需解决的问题。

近年来，灰色系统理论在处理“小样本”、“贫信息”的问题时，取得了显著的效果[5]，同时考虑到MSaaS的可信度评估只拥有少量的定量信息，往往较难评估。因此，本文提出了一种熵权法和灰色层次分析法相结合的可信度评估方法。

2 MSaaS仿真架构

目前MSaaS应用较多的是分层体系架构，其特点为：将系统的功能按层次划分为独立的层，其中每层均有一个接口可以向其它层提供操作。其一般架构图如图1所示[6]。

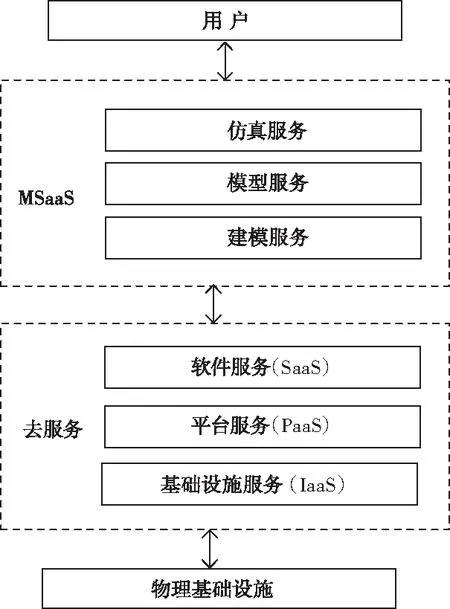
图1 MSaaS一般架构图

3 建立可信度评估指标

影响该架构可信度的因素主要为四大类：模型服务可信度、仿真服务可信度、云服务可信度和仿真结果可信度[7]。其递阶层次结构图如图2所示。

1)模型服务可信度。模型即服务可信度的影响因素主要由模型的可信度决定。由于仿真的项目不同，建立的仿真模型也不同，所建模型的正确性、完备性和精度等因素影响着模型即服务的可信度。

图2 建模即服务可信度递阶层次结构图

2)仿真服务可信度。该架构中仿真即服务的可信度主要由模型服务注册表的可信度、仿真引擎的可信度等因素决定。

3)云服务可信度。该架构云服务层以平台即服务(PaaS)和基础设施即服务(IaaS)构成，用于提供云计算、基础设施等服务，在用户进行仿真时提供数据，调度和分配资源。其可信度主要由数据传输可信度和调度与分配资源可信度决定。

4)仿真结果可信度。记录并保存多次仿真运行的结果，将仿真得到的数据与真实实验情况和经验数据进行对比，并通过专家评分来确定仿真结果可信度。

4 MSaaS可信度评估方法

灰色层次评估法以灰色系统理论为基础，以层次分析法为指导，是一种定量与定性相结合的评估方法。其优点是可以提高评估的精确度及有效性，但存在各个评估指标对于目标层的权重主观性太强、权重分配不够客观的不足[5]。如果在灰色层次评估法中引入熵权法，求评估指标对于目标层的权重，可以提高评价的合理性。关于熵权-灰色层次分析，其具体计算步骤如下：

1) 熵权法求权重

①专家评分

将指标的评分等级划分五个等级，以十分制进行评分。五个等级分别为极好(9-10分)、很好(7-9分)、好(5-7分)、较差(3-5分)、差(0-3分)。邀请相关领域专家根据仿真运行过程对底层元素(三级指标)进行评分，对所得评分进行无量纲化处理，计算公式如下。

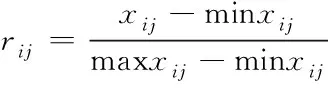
(1)

②计算信息熵概率

利用式(2)对无量纲化之后的数据进行预处理，得到信息熵发生的概率pij。

(2)

其中Mij为第i个专家对第j个三级指标的评分。

③计算信息熵

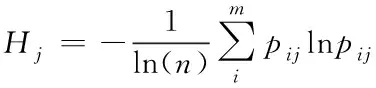
(3)

其中Hj为评价指标的信息熵；n为三级指标总数；m为参与评估的专家个数；i表示参与评分的专家的标号，j表示第j个三级指标；pij为各信息熵发生的概率，且pij≠0。

④计算权重

根据式(4)计算评估指标对于目标层的权重。其中Hj为评价指标的信息熵。

(4)

2) 层次分析法求权重

①建立判断矩阵

邀请相关领域的专家，根据1-9标度法对各级指标的重要性进行评分，由此建立判断矩阵。

②计算权重

计算式(1)中建立的判断矩阵的最大特征值及其对应的特征向量，并将其进行归一化得到每层元素相对上层元素的权重。各级指标算法相同，以此算出每层元素相对上层元素的权重，最后得到底层元素相对目标层的权重WAj。

③一致性检验

为保证计算结果的相对准确性，要进行一致性检验，其计算公式如下

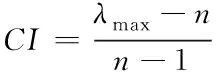
(5)

(6)

其中CR为一致性比例；CI为一致性指标；RI为平均随机一致性指标，其取值如表1所示；λmax为矩阵的最大特征值；n为矩阵的阶数。当CR<0.1时，认为判断矩阵具有可接受的一致性，否则需重新修正计算，直至一致性通过[5]。

表1 平均一致性随机指标

3)求组合权重

根据上述所求得的三级指标相对目标层的层次分析法权重WAj以及三级指标相对目标层的熵权法权重WEj，采用常用的乘数归一算法[8]可求得组合权重Wj，如式(7)所示。

(7)

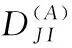
5)确定评估灰类

根据步骤1中专家对底层元素的评分以及划分的评估等级，可对应5个评估灰类，即N=1，2，3，4，5。如表2所示。

表2 评估等级取值范围

对于5个评估灰类，其相应的灰数及白化权函数如下：

1)第一灰类“极好”(N=1)，灰数⊗1∈[9，∞]，白化权函数为

(8)

2)第二灰类“很好”(N=2)，灰数⊗2∈[0，16]，白化权函数为：

(9)

3)第三灰类“好”(N=3)，灰数⊗3∈[0，10]，白化权函数为

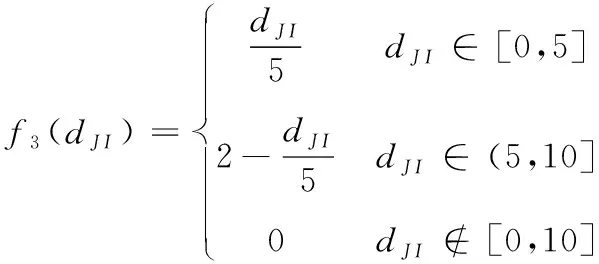
(10)

4)第四灰类“较差”(N=4)，灰数⊗4∈[0，6]，白化权函数为

(11)

5)第五灰类“差”(N=5)，灰数⊗5∈[0，3]，白化权函数为

(12)

6)计算灰色评估系数

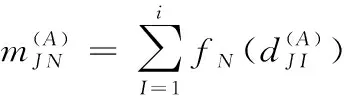
(13)

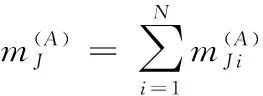
(14)

7)计算灰色评估权重

(15)

8) 计算综合聚类系数，给出评价结果

文献[6]中提出了综合聚类系数评价方法。仿真建模即服务可信度关于5个灰类的综合聚类系数分别定义为

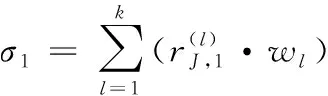
(16)

(17)

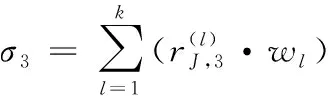
(18)

(19)

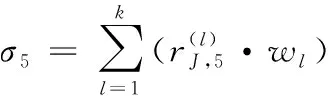
(20)

其中k表示有k个底层指标。

5 算例分析

下面以基于MSaaS战场环境仿真可信度评估为例。根据作战活动分布的范围及主要兵器运用的环境，现代战场可以分为陆地战场、海洋战场、天空战场、太空战场和电磁战场[9]。根据图2可以建立基于MSaaS的战场环境仿真可信度递阶层次结构图，如图3所示。

利用熵权法和层次分析法求得底层元素相对目标层元素的权重以及两者的组合权重如图4所示。

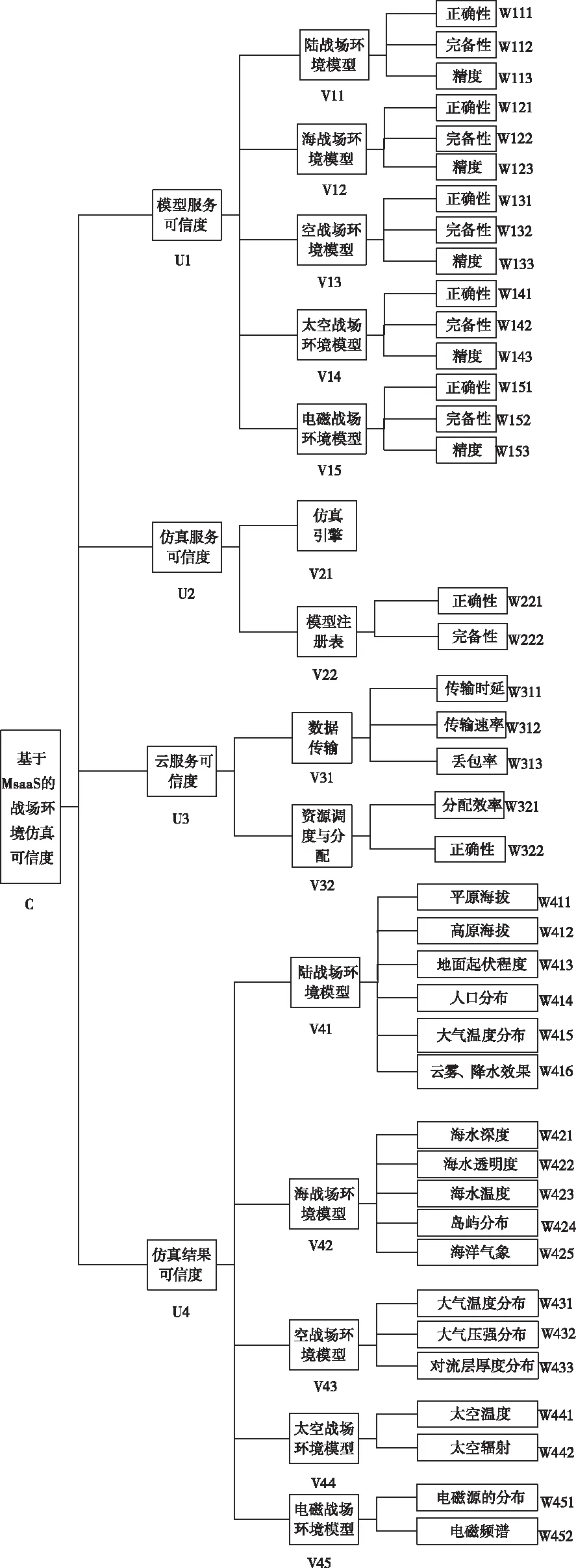
图3 战场环境仿真可信度递阶层次结构图

利用白化权函数可求得灰色评估系数，再计算灰色评估权重。灰色评估权重分布如图5所示。

图4 组合权重分布图

经计算可得5个灰类的综合聚类系数为：

图5 灰色评估权重分布图

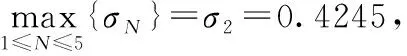
6 结论

针对MSaaS仿真架构可信度评估问题，考虑MSaaS架构中各基本要素之间的关系，建立了MSaaS可信度评估指标体系，将熵权法和层次分析法引入到灰色评估方法中，并以MSaaS战场环境仿真可信度评估为例，结果表明该评估方法有效。