考虑参数不确定性的滚珠丝杠副耐磨损确信可靠性建模与分析*
朱云开
(江苏城市职业学院 机电工程学院,江苏 南通 226006)
0 引 言
磨损作为机械零件的主要的失效形式之一,不仅会显著缩短机械产品的使用寿命,也会导致机械产品其他失效形式的产生。因此,对滚珠丝杠副的耐磨性进行可靠性分析和优化,有利于提高滚珠丝杠副的可靠性。这对整个传动系统的可靠性的提高有着重要的意义。
目前,针对滚珠丝杠副磨损的机理研究和理论建模研究已经有很多。
姜洪奎等人[1]总结了磨损失效的主要形式及失效原因,为磨损的计算机建模提供了理论依据。钟金豹等人[2]采用有限元仿真软件,分析了滚珠丝杠副的磨损特性,并基于表面织构化机理对其进行了仿真,结果发现,表面织构化能提高滚珠丝杠副的耐磨性。基于Archard理论,赖建林等人[3,4]建立了高承载下的滚珠丝杠副黏着磨损模型。基于蠕滑理论,陈勇等人[5]建立了摩擦力矩模型,为能够快速、准确地预测滚珠丝杠副的磨损量提供了理论基础。基于Archard理论,徐向红等人[6]在充分考虑了轴向载荷、接触面的相对速度、离心力和陀螺力矩等影响的基础上,建立了滚珠丝杠副磨损量模型。陈斌斌等人[7]在传统的Archard理论基础上,引入修正系数,建立了反映滚珠丝杠副滚道与滚珠真实接触情况的磨损量模型。ZHOU C G等人[8,9]在考虑了载荷分布影响的基础上,建立了滚珠丝杠副的磨损模型,并通过试验获得了滚珠丝杠副的磨损系数。
上述有关于滚珠丝杠副磨损的研究,仅局限于滚珠丝杠副的磨损特性,并未对其耐磨损性能及耐磨损可靠性进行研究。
耐磨损可靠性是滚珠丝杠副整体可靠性的一部分,因此,针对其开展研究也是必不可少的。
ZHOU C G[10]在其建立的磨损模型基础上,基于一次二阶矩法,对滚珠丝杠副进行了可靠性分析,并计算了各参数对滚珠丝杠副磨损影响的灵敏度,根据计算结果对滚珠丝杠副进行了优化设计,显著提高了滚珠丝杠副的耐磨损可靠度,但该方法仅考虑了参数的随机不确定性,而未考虑认知不确定性的影响。
由于滚珠丝杠副耐磨损可靠度受多个参数的影响,且其分布参数存在不确定分布,确信可靠性指标不再为确定的值,而变成了不确定变量,存在不确定分布。当确信可靠度指标是关于分布参数的单调函数时,可以通过逆不确定分布很方便的求出其不确定分布[11]。但是,对于滚珠丝杠副耐磨性的确信可靠度指标,其并非分布参数的单调函数,因此,不能采用上述方法求得其精确的不确定分布。
朱元国[12]基于最大不确定性原理,提出了不确定仿真的方法,用于求解不确定分布的上、下界;但是该方法只是针对单层不确定参数进行求解。ZHANG Q Y[13]基于上述不确定仿真方法,提出了两层参数不确定分析方法,该方法同时考虑了参数本身的不确定性及参数分布的不确定性;但该方法只是局限于理论部分,并未在实际中予以应用。
笔者基于上述提出的不确定仿真方法,考虑滚珠丝杠副参数本身的不确定性,及其分布的参数的不确定性这两层参数不确定性的影响,对滚珠丝杠副耐磨损的确信可靠性进行建模与分析;同时,分析各参数的不确定性对滚珠丝杠副的耐磨损可靠度的影响程度,为滚珠丝杠副的优化设计和可靠性提升提供参考价值。
1 不确定理论
不确定理论是刘宝碇提出来的一种新的公理化理论[14],被认为是更为合理地描述认知不确定性的数学理论。无论是在概念和逻辑上,不确定理论与概率论相比,都有着较大差距。
在概率论中,通常用概率来量化事件发生的可能性大小;而在不确定性理论中,则采用不确定测度来表征人们对事件的主观确信程度,即某件事件确定后其概率一般是确定的。而不确定测度与人的知识有关,会随着人们对事件的了解程度的变化而发生改变。
在某个事件中,当其不确定测度为1时,其不确定性最小,表示该事件必然发生;当其不确定度测度为0时,其不确定性也是最小的,表示该事件必然不发生;当不确定测度为0.5时,不确定测度才最大。
根据最大不确定性原理,当某个事件的不确定测度存在多个可能的值时,取最接近0.5的那个值作为其不确定测度[15],即:
(1)
在不确定理论中,通过不确定分布来描述不确定变量的确信程度。若ξ为线性不确定变量,即ξ~L(a,b),其不确定分布为:
(2)
若ξ为正态不确定变量,即ξ~N(e,σ),其不确定分布为:
(3)
2 滚珠丝杠副耐磨性建模分析
在传统的Archard理论中,假设两滑动接触面是始终接触的。然而对于滚珠丝杠副而言,只有螺母内部的丝杠与滚珠接触,且螺母和丝杠的滚道只有部分参与接触,因此,必须对传统的Archard理论进行修正。
笔者首先基于传统的Archard理论计算出滚道与滚珠的磨损体积,然后基于赫兹接触理论求出滚道与滚珠的接触面积,最后引入修正系数,求出其磨损的深度。
2.1 滚珠与滚道之间的磨损体积计算
由传统Archard磨损理论[16]可知,在法向力Q作用下,滚珠丝杠副的滚道与滚珠磨损原理图如图1所示。
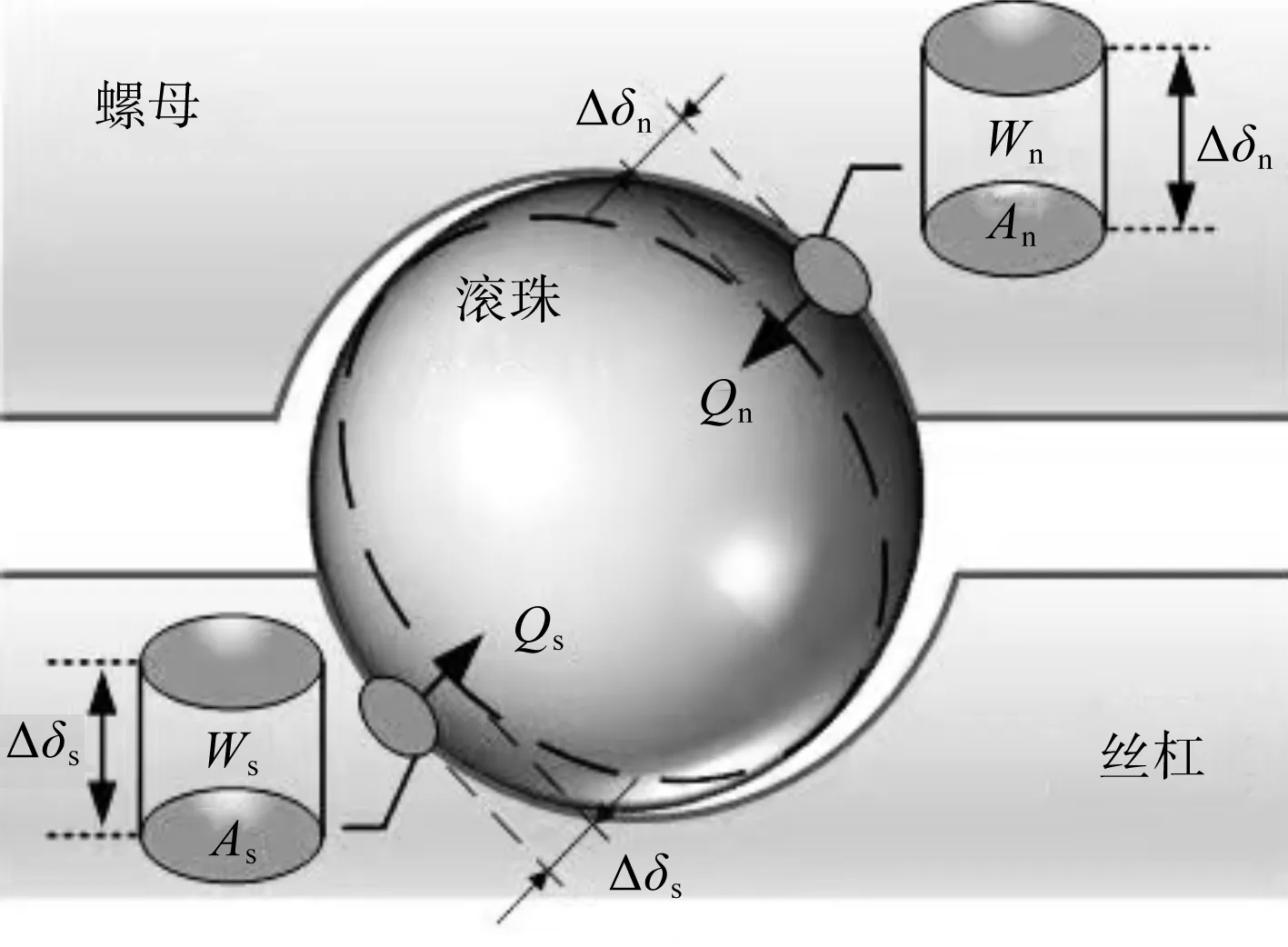
图1 滚道与滚珠磨损原理图
滚珠丝杠副的滚珠与螺母或丝杠滚道的磨损体积为:
(4)
式中:Ws—滚珠与丝杠滚道接触面之间的磨损体积,m3;Wn—滚珠与螺母滚道接触面之间的磨损体积,m3;Qs—滚珠与丝杠滚道接触面之间的法向力,N;Qn—滚珠与螺母滚道接触面之间的法向力,N;H—滚珠和滚道中硬度较小即软材料表面的硬度,一般为螺母滚道或者丝杠滚道的硬度;Ls—滚珠相对于丝杠滚道的滑动距离,m;Ln—滚珠相对于螺母滚道的滑动距离,m;K—磨损系数。
对于双螺母滚珠丝杠副而言,在无外载荷时,螺母1和2只受初始预紧力Fp,当滚珠丝杠承受轴向载荷Fa时,滚珠丝杠副受力示意图如图2所示。
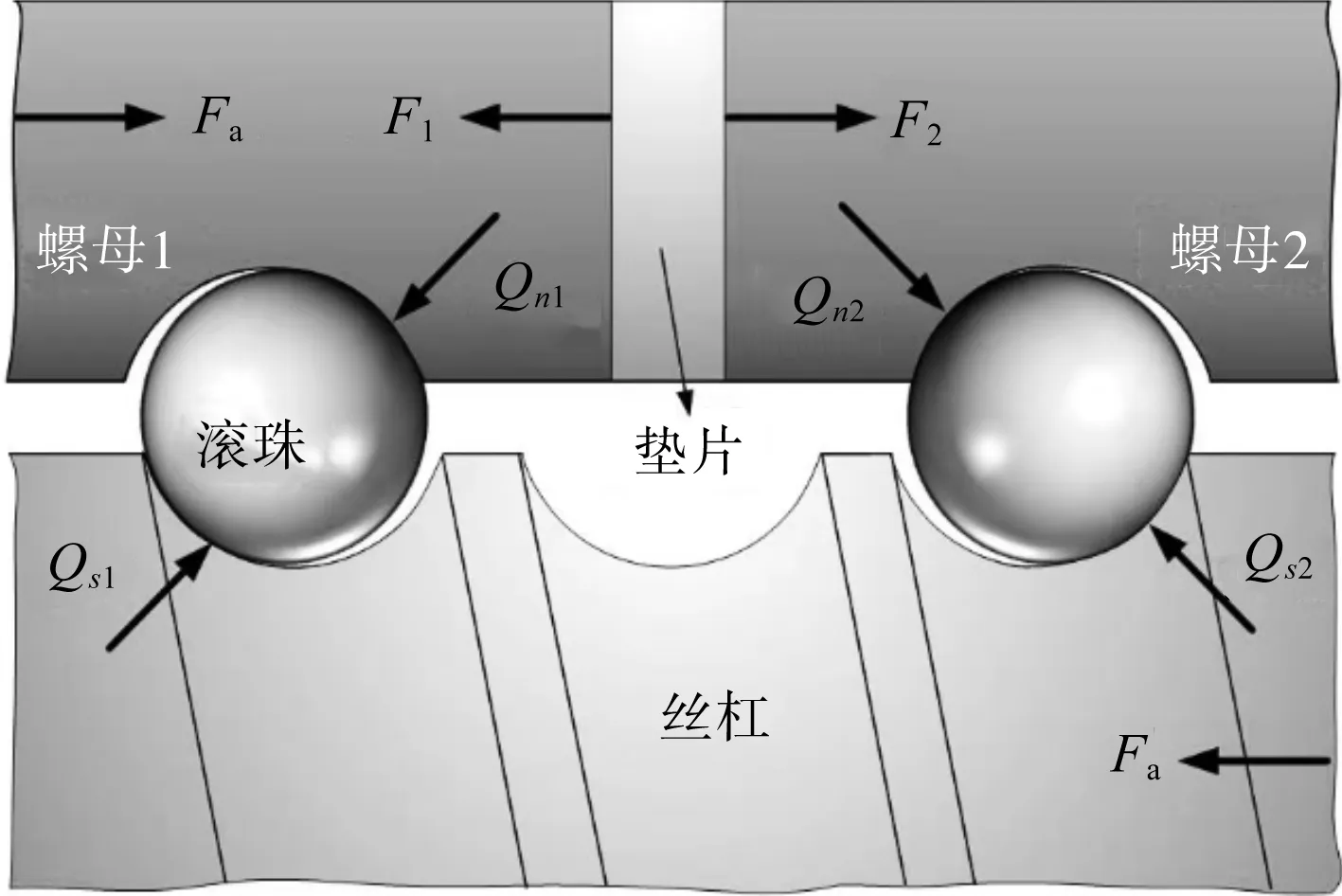
图2 滚珠丝杠副受力示意图
图2中,此时螺母2为工作螺母,实际受力由Fp增加为F2;螺母1为预紧螺母,实际受力由Fp减少为F1。
故存在等式:
F2-F1=Fa
(5)
由变形协调关系可知:
(6)
可求得F2,则F1为:
F1=F2-Fa
(7)
对于螺母1,由静力平衡方程可知,滚珠承受法向力为:
(8)
对于螺母2,由静力平衡方程可知,滚珠承受法向力为:
(9)
式中:α—滚珠与滚道的接触角,(°);γ—丝杠螺母的导程角,(°);i—滚珠丝杠副单个螺母中滚珠循环圈数;Z—每圈承载滚珠数。
其滚珠相对于丝杠滚道或螺母滚道的滑动距离Ls和Ln分别为:
(10)
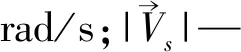

(11)
其中:
(12)
滚珠相对于螺母滚道的滑动速度可表示为:
(13)
(14)
对于螺母1,滚珠与丝杠滚道或螺母滚道接触面间的磨损体积为:
(15)
对于螺母2,滚珠与丝杠滚道或螺母滚道接触面间的磨损体积为:
(16)
2.2 滚珠与滚道的接触面积计算
由赫兹弹性接触理论可知,滚珠与丝杠或螺母滚道的接触面为椭圆,其接触面积为:
(17)
式中:as—滚珠与丝杠滚道接触椭圆面的长半轴,mm;
an—滚珠与螺母滚道接触椭圆面的长半轴,mm;bs—滚珠与丝杠滚道接触椭圆面的短半轴,mm;bn—滚珠与螺母滚道接触椭圆面的短半轴,mm。
根据接触变形理论,椭圆的长半轴和短半轴为:
(18)
(19)
式中:mas—丝杠的无量纲接触椭圆长半轴;man—螺母的无量纲接触椭圆长半轴;mbs—丝杠的无量纲接触椭圆短半轴系数;mbn—螺母的无量纲接触椭圆短半轴系数;E′—当量弹性模量,Pa。
联立式(17~19),即可求出滚珠与螺母滚道或丝杠滚道的接触面积。
对于螺母1一侧,丝杠和螺母的接触面积为:
(20)
对于螺母2一侧,丝杠和螺母的接触面积为:
(21)
2.3 磨损深度计算
联立式(15,16,20,21),经计算得到滚珠与滚道的接触深度为:
(22)
(23)
滚珠与滚道实际接触原理图如图3所示。
根据周长光[17]的研究及图3可知:滚道与滚珠的接触椭圆与主要磨损区域的重叠部分,近似为宽度是2b的矩形,因此,此处笔者引入修正系数为:

图3 滚珠与滚道实际接触原理图
(24)
式中:ls—丝杠的有效行程,mm;ln—螺母的有效行程,mm。
故对于单个滚珠,其与滚道之间的磨损深度为:
(25)
(26)
反行程时螺母1和正行程时螺母2的法向力相同,磨损深度相同;同理,反行程时螺母2和正行程时螺母1的法向力相同,磨损深度也相同,因此,对于整个运行过程而言,丝杠和螺母的磨损深度取两者的平均值。
由此可得滚珠与滚道的总磨损量为:
δN=i·Z·(Δδs+Δδn)=
(27)
3 滚珠丝杠耐磨损确信可靠性分析
根据式(27)建立的滚珠丝杠副磨损模型,笔者建立滚珠丝杠副耐磨性的性能裕量m表达式为:
m=f(x)=δ0-δ=δ0-
(28)
式中:x—轴向载荷Fa、丝杠节圆直径Dpw、滚珠直径dw、适应比f、接触角α、导程角γ、磨损系数K组成的向量。
根据可靠性的定义,滚珠丝杠副耐磨损可靠度为:
R=P{m>0}
(29)
根据经验,轴向载荷Fa、丝杠节圆直径Dpw、滚珠直径dw、适应比f、接触角α、导程角γ、磨损系数K参数服从概率分布,但是其分布的参数并非定值。由于难以收集到足够的数据对其进行估计,因此,这些分布的参数存在不确定性,从而导致滚珠丝杠副耐磨性的性能裕量和可靠度也是不确定变量。
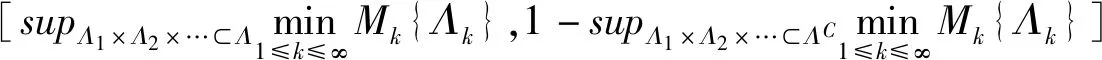
基于此原理,可以采用如下步骤求出滚珠丝杠副耐磨损可靠度的不确定分布:
步骤1。确定滚珠丝杠副磨损量中各参数服从的概率分布xi~Qi(ai,bi)(i=1,2,…,7,分别代表7个影响参数)及分布参数的不确定分布ai~Ri(ci,di)。其中,xi分别代表轴向载荷Fa、丝杠节圆直径Dpw、滚珠直径dw、适应比f、接触角α、导程角γ、磨损系数K;


步骤4。结合建立的滚珠丝杠副耐磨损性能裕量模型,对步骤3中的N组概率分布,分别采用蒙特卡洛法[18]求取滚珠丝杠副耐磨性的可靠度R(k)(k=1,2…,N);
步骤5。给定初值γ=0,求解不确定变量RB<γ的机会测度的上下界ΨU(RB)、ΨL(RB)。
其具体步骤包括:
(1)设置初始值m1(i)=0、m2(i)=0,其中,i为输入参数变量xi的下角标,i=1,2,…,7;


(4)计算:
(30)
式中:“Λ”—取小符号,即取其中最小值;



(7)不确定变量RB<γ的机会测度的上下界ΨU(RB)、ΨL(RB)分别为ΨU(RB)=RU、ΨL(RB)=RL。
步骤6。令γ=γ+Δγ,重复步骤5,求取不同确信可靠度的机会测度的上下界,直至γ=1,其中,Δγ为预设的取值间隔。
通过这个算法,可以得到不同可靠度RB取值时的不确定分布的上下界(ΨL(RB),ΨU(RB))。
根据定义,滚珠丝杠副耐磨损的平均确信可靠度为:
(31)
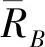
(32)
式中:ΔRBi—取值的间隔,即为Δγ;ΨU(RBi)-第i次迭代得到的确信可靠度RBi对应的下界;ΨL(RBi)-第i次迭代得到的确信可靠度RBi对应的下界;n-迭代的总次数。
通过该算法,还能够得到不同信度水平下的可靠度区间,即:.
[VaRL,VaRU]{ζ}=[sup{RB|ΨU(RB)≤ζ},sup{RB|ΨL(RB)≤ζ}]
(33)
式中:ζ—信度水平;VaRL—可靠度区间的上界;VaRU—可靠度区间的下界。
4 实例分析
此处的计算采用丝杠为1004内循环滚珠丝杠副,假设滚珠丝杠副的节圆直径Dpw、接触角α、导程角γ、适应比f、滚珠直径dw、轴向载荷Fa、磨损系数K等参数服从正态分布,且参数的均值服从不确定分布,方差确定,为第一层参数,参数的均值服从正态不确定分布,为第二层参数。
滚珠丝杠副参数的双层不确定性表征如表1所示。

表1 滚珠丝杠副参数的双层不确定性表征
结构参数、材料参数及工况参数表如表2所示。

表2 结构参数、材料参数及工况参数表
案例仿真用滚珠丝杠副如图4所示。

图4 案例仿真用滚珠丝杠副
通过仿真计算,求得耐磨损可靠度不确定分布图如图5所示。

图5 耐磨损可靠度不确定分布图
从图5中可以看出:滚珠丝杠副可靠度的不确定分布上下界都为阶梯递增,通过式算得考虑参数的不确定性时滚珠丝杠副确信可靠度为0.656 522,而不考虑其参数的不确定性,即通过蒙特卡洛法算得其概率可靠度为0.770 07;可见,参数的不确定性对滚珠丝杠副的可靠性有很大影响,其参数的不确定性,会导致滚珠丝杠副可靠度显著降低;
同时,从图5中可以看出,[VaRL,VaRU]{0.9}=[0.649 5,0.999 5],即90%的信度认为滚珠丝杠副的耐磨损可靠度位于区间[0.649 5,0.999 5]之间。
所计算的滚珠丝杠副耐磨性可靠度如表3所示。

表3 滚珠丝杠副耐磨性可靠度
5 基于两层参数不确定的可靠性影响分析
上文通过不确定仿真的方法求出了滚珠丝杠副耐磨损可靠度,计算结果表明,参数的不确定性对于滚珠丝杠副的可靠度提升具有较大影响。可见,为了提高其可靠度,保证可靠度满足使用要求,必须降低各参数的不确定性。
因此,研究各参数的不确定性对滚珠丝杠副耐磨损可靠度的影响程度十分必要。
滚珠丝杠副的耐磨损可靠度主要受轴向载荷Fa、丝杠节圆直径Dpw、丝杠和螺母滚道适应比f、接触角α、导程角γ、滚珠直径dw、磨损系数K等参数的影响。笔者将采用上文给出的两层参数不确定仿真算法,研究各参数对滚珠丝杠副耐磨损可靠性的影响程度。
考虑各参数不确定性的可靠度不确定分布如图6所示。


图6 考虑各参数不确定性的可靠度不确定分布
从图6中可以看出:只考虑单参数后的可靠度不确定分布图,其阶梯变化幅度更小,曲线走势更加平缓,说明考虑的不确定因素越多,对滚珠丝杠副的可靠度影响越明显;
从不确定分布的变化幅度看,考虑适应比、滚珠直径的不确定性时,其走势相对更加陡峭,其次是考虑接触角、轴向载荷、节圆直径、磨损系数的不确定性;考虑导程角的不确定性时,其走势更加平缓,这说明,在适应比、滚珠直径等因素的不确定影响下,滚珠丝杠副的可靠度分布较为集中,在导程角的不确定性影响下,滚珠丝杠副的可靠度分布较为分散。
由此可见,相对于适应比和滚珠直径等因素,导程角的不确定性对滚珠丝杠副的可靠度的影响更大。
为更加直观地表征各参数不确定性对丝杠副耐磨损可靠度的影响程度,笔者通过式(32)求得了各参数不确定性的确信可靠度,如表4所示。
从表4可以看出:考虑不确定性的参数个数越多,可靠度越小,这说明参数不确定性的存在不利于滚珠丝杠副可靠性的提升;
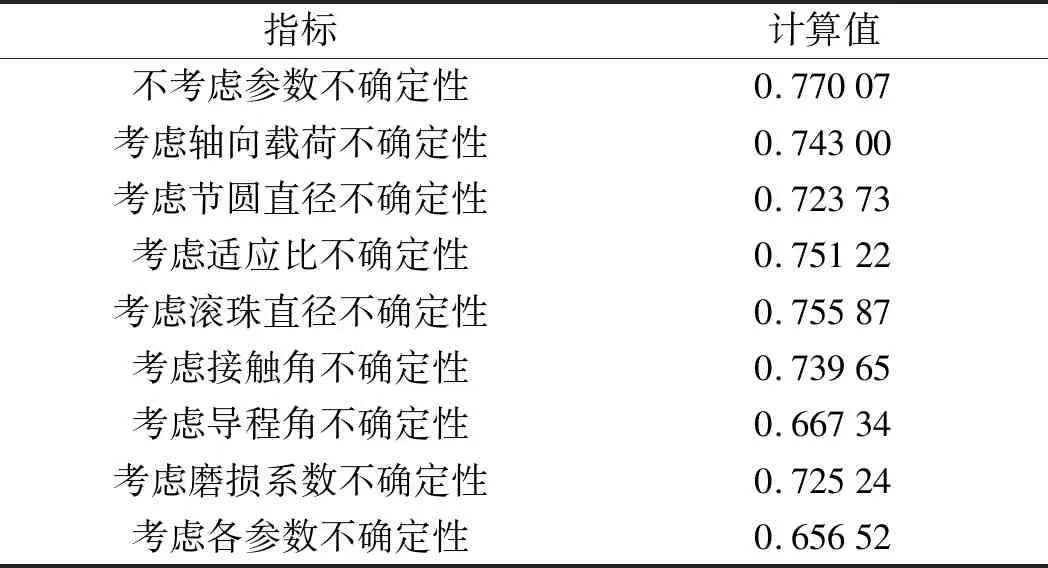
表4 各参数不确定性的确信可靠度
在影响滚珠丝杠副耐磨损可靠性的各参数中,考虑滚珠直径的不确定性时,其确信可靠度最大,相对于不考虑参数不确定性时,其可靠度下降幅度最小,这说明,滚珠直径的不确定性对于滚珠丝杠副耐磨损可靠度的影响最小,其次是适应比、轴向载荷、接触角、磨损系数、节圆直径。而考虑丝杠导程角的不确定性时,可靠度最小,下降幅度最大,可见导程角的不确定性对滚珠丝杠副的可靠性影响最大。
由此可见,为提高滚珠丝杠副的耐磨损性能,首先必须降低导程角的不确定性,通过改良工艺来保证滚珠丝杠副的导程满足设计要求;其次是提高加工精度,保证节圆直径的可靠,降低加工误差;并且在选材和材料的表面热处理上加以优化,以保证材料的摩损系数可控,符合设计要求。
此外,接触角、适应比和滚珠直径等参数的不确定性也对丝杠的可靠性有较大影响,因此,在设计阶段也应尽量降低其不确定性。
6 结束语
在传统的滚珠丝杠副的耐磨损可靠性计算中,只考虑随机不确定性,而未考虑认知不确定性,针对这一问题,笔者基于不确定理论,建立了一种既考虑参数随机不确定性,又考虑认知不确定性的滚珠丝杠副耐磨性可靠度模型;
笔者针对滚珠丝杠副耐磨损可靠度的精确的不确定分布难以求出的问题,基于最大不确定性原理,提出了一种两层参数不确定仿真方法。通过该方法,求出了滚珠丝杠副耐磨损确信可靠度和可靠度信度区间;同时,采用该算法分析了各参数不确定性对滚珠丝杠副耐磨损可靠度的影响程度。
研究结论如下:
(1)参数不确定性的存在会显著降低滚珠丝杠副耐磨损可靠度,不利于产品的可靠性提升;
(2)各参数的不确定性对于产品的可靠度影响是叠加的,即参数的不确定性越多,可靠性越小,越不利于产品可靠性的提升;
(3)在影响滚珠丝杠副的耐磨损可靠度的因素中,导程角的不确定性影响最大,其次是节圆直径、磨损系数、接触角、轴向载荷、适应比,滚珠直径的影响最小。
因此,应改良滚珠丝杠副的加工工艺,减少滚珠丝杠副的导程误差和节圆直径误差,同时应在选材和表面热处理上加以优化,以使材料的磨损系数符合设计要求。
鉴于当前的滚珠丝杠副磨损建模过程中,存在一定程度的简化,因此,在后续的工作中,笔者将进一步深入开展滚珠丝杠副磨损特性研究,以完善所当前建立的磨损模型和可靠性模型。
——对2018年广州市一道中考题的研究

