基本不等式与其他知识的交汇融合

丁建兵

⦿江苏省西亭高级中学

本文中归纳总结了基本不等式与其他知识交汇融合的6种常见题型，并结合具体实例进行分析求解，以引导学生通过总结归纳强化和提升对相关知识、方法的综合运用能力.

1 常见题型一：基本不等式与函数的交汇

求解有关代数式的范围或最值时，往往需要适当构造函数，在数形结合的基础上，利用基本不等式或者基本不等式的变形结论加以灵活求解.

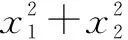
C.(2,+∞) D.(0,1)

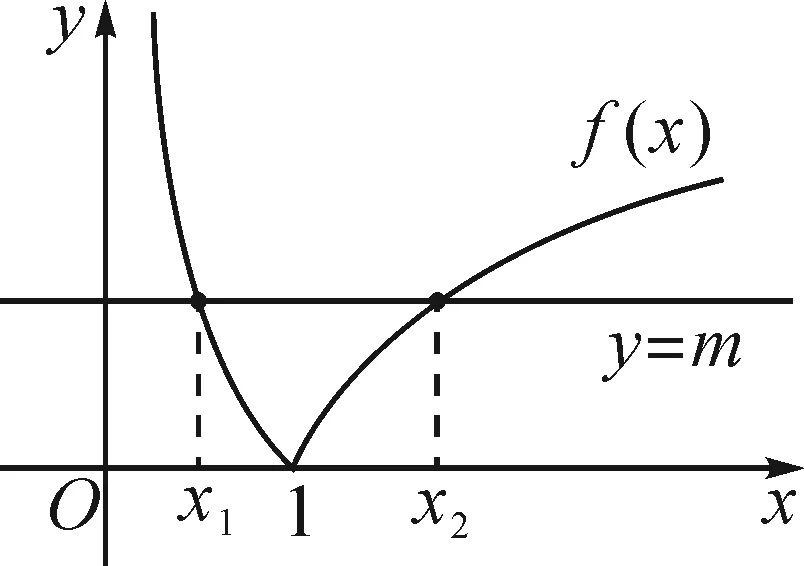
图1

解析：如图1，在同一坐标系中分别画出函数f(x)=|lnx|的图象与直线y=m.根据题意可知函数y=|lnx|的图象与直线y=m有两个不同的交点，且交点的横坐标分别为x1和x2，不妨设x11.

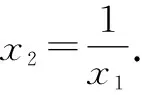
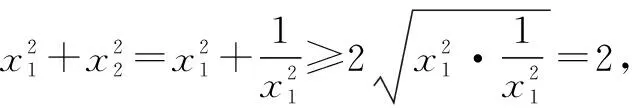
故选：C.

评注：本题求解的关键有三点.一是活用数形结合思想转化题设已知条件；二是根据方程的根，获得x1x2=1；三是借助基本不等式，准确求解目标式的取值范围.

2 常见题型二：基本不等式与数列的交汇

以数列知识为背景而设置的求解最值问题，需要先根据等差数列、等比数列知识进行具体分析，以便适当转化目标式(写成一元代数式)，再灵活运用基本不等式即可顺利获解.

例2已知递增等差数列{an}中，a1a2=-2，则a3的( ).

A.最大值为-4 B.最小值为4

C.最小值为-4 D.最大值为4或-4

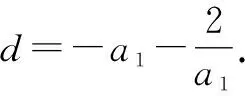
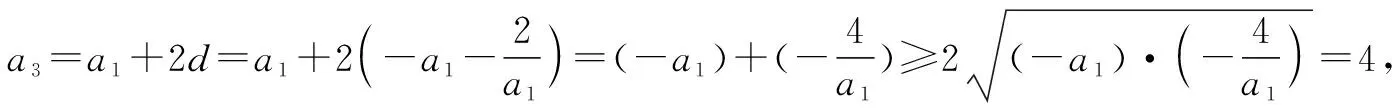
故选：B.

评注：本题看似简单，但实则考查了等差数列的通项公式、单调性与基本不等式在求解最值问题中的综合运用，且求最值时极易出错(没有关注基本不等式成立的前提条件).

3 常见题型三：基本不等式与向量的交汇

处理平面向量中的有关最值问题时，往往需要在数形结合的基础上，先根据平面向量知识分析获得一个具体的结论，再利用该结论以及基本不等式灵活求解目标式的最值问题.

图2

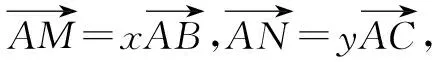
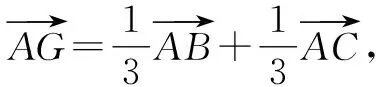
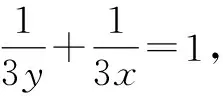
评注：本题主要考查了基底向量与向量的共线定理、性质在解题中的综合运用，同时也考查了利用基本不等式巧求目标代数式的最小值(需要借助“1”的特性灵活变形).

4 常见题型四：基本不等式与直线和圆的交汇

处理直线和圆中的有关取值范围问题时，需要先根据直线与圆的位置关系进行分析获得一个具体的结论，再借助基本不等式或者基本不等式的推广性结论加以灵活求解.

例4设m,n∈R，若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切，则m+n的取值范围是( ).

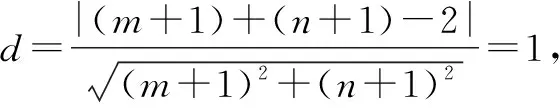
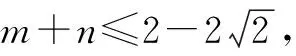
故选：D.

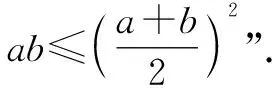
5 常见题型五：基本不等式与立体几何的交汇

以立体几何为背景而设置的最值求解问题，需要先根据空间图形以及立体几何相关知识进行具体分析，进而灵活运用基本不等式即可顺利获解.

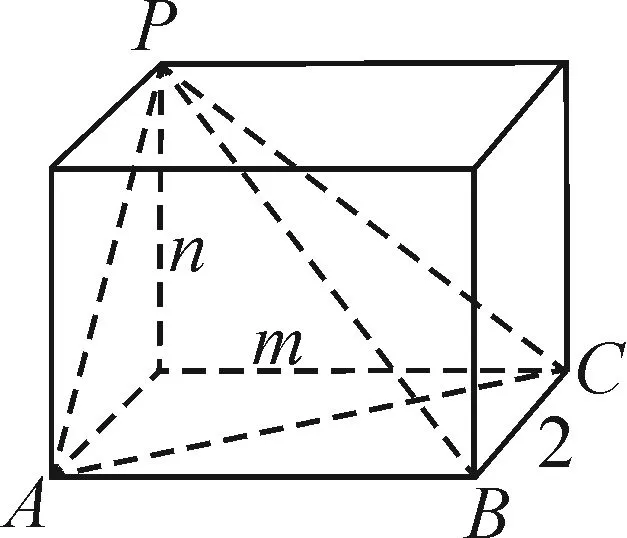
图3

例5如图3，三棱锥P-ABC的四个顶点恰是长、宽、高分别是m,2,n的长方体的顶点，若此三棱锥的体积为2，则该三棱锥外接球体积的最小值为.

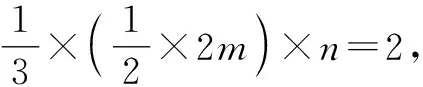
评注：本题主要考查了三棱锥的体积公式、球的体积公式以及基本不等式在解题中的综合运用，有利于较好地培养学生的空间想象能力以及数形结合能力.

6 常见题型六：基本不等式与解三角形的交汇

处理解三角形中的有关最值问题时，往往需要先根据正弦定理、余弦定理、面积公式以及相关三角函数知识进行综合分析，再灵活运用基本不等式即可顺利获解.

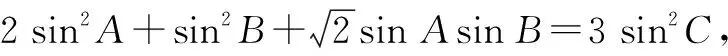
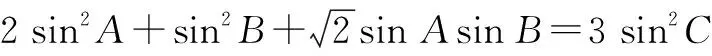
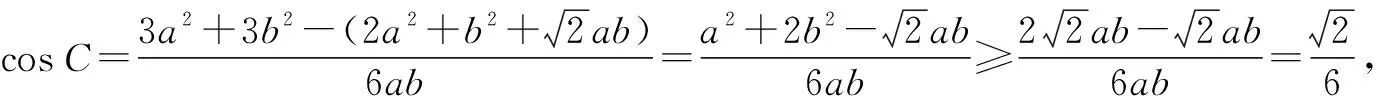
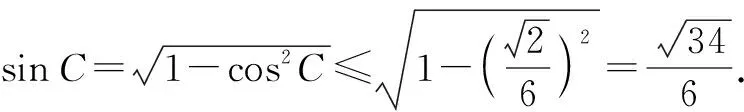
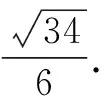
评注：本题主要考查了正弦定理、余弦定理以及基本不等式在解题中的综合运用，有利于较好地培养学生数学运算、逻辑推理等核心素养.

总之，在处理有关范围或最值问题时，应适时创造有利条件，以便灵活运用基本不等式获得巧思妙解，进而提高解题的技能技巧，且学且悟且提升！