600km·h-1高速磁浮列车气动噪声仿真与试验分析

陈雨豪，葛剑敏，丁叁叁，朱雷威，郭建强

（1.同济大学 物理科学与工程学院，上海 200092；2.中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

高速磁浮列车因其速度快、运行平稳、耗能少及无污染等特点，成为未来交通运载工具发展的新方向。高速磁浮列车通常采用常导电磁悬浮系统，主要包含推进及辅助设备噪声、车体表面结构振动辐射噪声及空气动力性噪声3类噪声源。空气动力性噪声主要由偶极子和四极子声源组成，其辐射声功率与列车运行速度的6～8次方成正比［1］。随着磁浮列车运行速度不断提高，气动噪声将超过其他噪声成为最主要的噪声源。噪声问题已成为制约磁浮列车运行速度的主要因素，研究高速磁浮列车车外流场特性、气动噪声源分布及远场噪声辐射特性对未来降低高速磁浮列车气动噪声具有重要意义［2］。

因当前全球范围内投入运营的高速磁浮列车数量较少，对其气动噪声的研究较匮乏。气动噪声与列车外表面形状有最直接的关系，高速轮轨列车与磁浮列车在外形和尺寸方面有很强的相似性，因此可参考高速轮轨列车气动噪声的研究方法研究高速磁浮列车。交通运载工具气动噪声的研究方法主要包括实验法和数值模拟法。在线实车测试可获得最直接的气动噪声数据，在德国埃姆斯兰对TR08 磁浮列车车外噪声测试结果显示，当列车运行速度达到400km·h-1时，距离线路30.5m处的声暴露级达到100dB（A）［3］。毕海权等［4］根据可压缩黏性流体N-S方程和k-ε湍流模型对运行速度为430km·h-1的TR高速磁浮列车湍流流场进行数值计算，结果表明列车周围的速度和压力波动随着与列车表面距离的增大而减小，尾流区形成2 个旋转方向相反的涡。Zhang 等［5］用延迟分离涡模拟（DDES）和FWH 方程对250km·h-1高速列车气动噪声进行仿真计算，通过风洞试验验证了计算模型的准确性，设计了一套低噪声结构方案，平均声压级可降低3.2dB（A）。Sun等［6］采用非线性声学求解器（NLAS）方法研究运行速度为300km·h-1的高速列车近场气动噪声，利用声学表面求解 FW-H 方程进行远场气动噪声研究，结果表明，高速列车的车头和车尾是主要噪声源，由于尾部流动中的非定常流动结构，车尾的整体噪声水平高于车头。Wei等［7］基于Lighthill 声比拟理论，采用大涡模拟（LES）和FW-H 方程对400km·h-1高速列车气动噪声进行数值模拟，结果表明高速列车气动噪声的能量集中在1 000Hz～4 000Hz 频率范围内。Tan 等［8］采用K-FWH 方程和三维可压缩大涡模拟（LES）方法对600km·h-1高速列车进行气动噪声仿真计算，研究表明，偶极子和四极子对高速列车气动噪声总能量的贡献率不同，上游测点气动噪声能量主要来源于偶极子声源，下游测点气动噪声能量主要为偶极子和四极子声源。

目前对于高速磁浮列车气动噪声的试验与数值仿真研究较少，对高速轮轨列车气动噪声仿真计算通常采用FW-H 方程积分法或边界元法，由于列车运行马赫数较低，往往忽略空间四极子声源，且该方法很难研究列车近场噪声特性。本文考虑空气的可压缩性和空间四极子声源，以TR08 高速磁浮列车为研究对象，采用分离涡模拟计算列车周围非定常流场，基于Lighthill 声比拟理论和声学有限元方法计算列车近场和远场气动噪声，研究气动噪声的频谱特性、空间分布特性和随速度的增长规律。对上海磁浮线上的TR08 高速磁浮列车进行在线实车试验，将车体表面及远场噪声的试验与仿真数据进行对比，验证计算模型的可靠性。

1 流体数值分析和气动噪声计算方法

1.1 分离涡模拟

分离涡模拟是一种将非定常雷诺平均法（URANS）和大涡模拟法相结合的混合方法。在近壁区域，采用非定常RANS湍流模型模拟流动中的小尺度脉动；在以大湍流尺度为主的分离流动区，采用具有亚格子尺度（SGS）的大涡模拟模型。DES方法已被广泛应用于高速列车外流场的计算，基于剪切应力输运（SST）湍流模型的DES方法基本方程为

式中：t为时间；ρ为流体密度；k为湍动能；ω为相对湍流耗散率；xi为笛卡尔坐标分量，i=1，2，3；ui为速度分量；μ为动力黏性系数；μt为涡黏系数；β为经验常数；Gk为由平均速度梯度产生的湍动能生成项；Gω为相对湍流耗散率生成项；σk和σω分别为k和ω的湍流普朗特数。

其中，F1为第一类混合函数。

其中，y为第1层网格到壁面的最小距离。

其中，S为应变率张量幅值；F2为第二类混合函数。

FDES的表达式为

式中：Δmax为最大网格间距；α*、a1、β*、σk，1、σk，2、σω，1、σω，2、Cdes均为经验常数。在靠近壁面的边界层区域，ω值较大，湍动能k较小，FDES值取1，SST 两方程湍流模型被激活。在距离壁面较远的湍流核心区，湍动能k较大，FDES取第1项，模型转化为具有亚格子尺度的大涡模拟模型［9-11］。

1.2 声比拟及声学有限元理论

声比拟方法（AAA）将声场计算分为2 步，第1步是根据计算流体动力学（CFD）求解流体的非定常流动方程，将求解结果作为噪声源，第2步是求解声波波动方程，解决声波从近场到远场的传播问题。Lighthill 将流体流动的连续性方程和动量方程重新变换，得到了气动噪声波动方程，如式（10）：

式中：c0为声速；Tij为Lighthill应力张量。

式中：p为压强；τij为黏性应力张量；δij为Kronecker delta符号。将Lighthill方程由时域转换为频域，得

式中：ω0为声波圆频率。用有限元法求解以上方程，选取基函数Na作为检验函数，令方程左右两边同时乘以基函数并进行体积分，使积分方程成立的解即为方程的近似解，这种方法称为伽辽金方法，形式为

利用分部积分、高斯定理和动量守恒方程，得

式中：ni为积分面法向单位矢量的i方向分量。方程左边为声波算子，方程右边为声源项，从CFD 的求解结果中提取。右边第1项代表面声源项，第2项代表体声源项。

2 高速磁浮列车计算模型

2.1 几何模型

采取TR08 高速磁浮列车为研究对象，利用三维建模软件建立列车与桥梁几何模型，如图1所示。列车模型分为形状完全相同的头车和尾车2 节车厢，车体表面简化为光滑曲面，忽略车门、车窗、列车车厢连接处等车体表面细小突出物，将轨面假定为光滑平面，忽略电磁铁、桥墩以及轨道梁之间的间隙。一节车厢的长度L、宽度W和高度H分别为27.1m、3.7m 和4.2m，车体流线型部分长度为5.2m，桥面宽度为2.6m。

图1 磁浮列车与桥梁几何模型Fig.1 Geometry model of maglev train and bridge

2.2 计算域和边界条件

计算域的大小主要考虑计算精度和内存需求，在保证计算精度的同时尽量减少计算域尺寸，以提高计算效率。桥上高速磁浮列车流场计算域如图2所示，头车鼻尖与入口的距离为L，尾车鼻尖与出口的距离为2L，为了保证列车尾部流场的充分发展。轨面到计算域下底面的距离为2H，轨面到计算域上顶面的距离为3H，计算域宽度为6W。

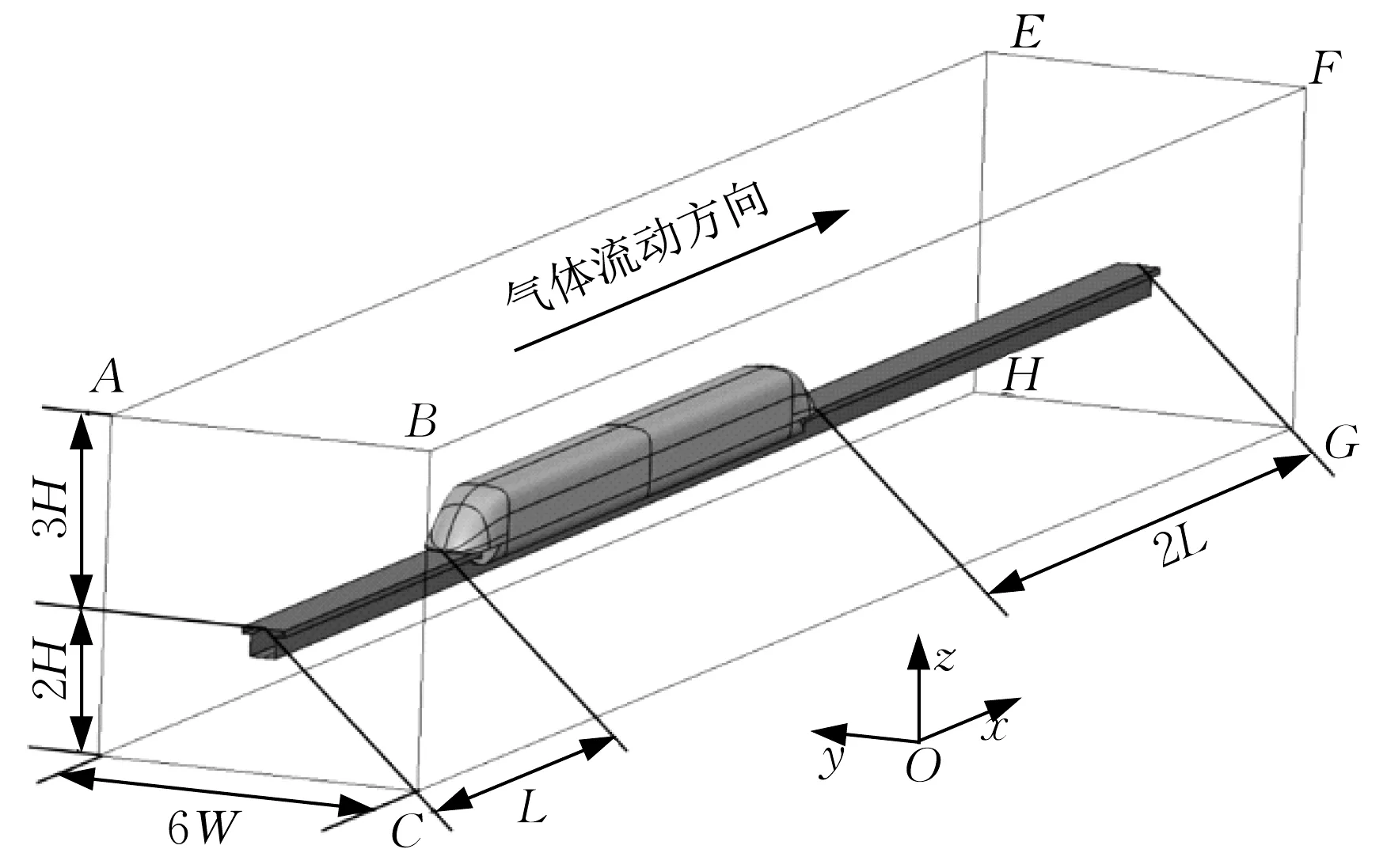
图2 高速磁浮列车计算域Fig.2 Computational domain of high-speed maglev train

马赫数（Ma）反映了单位质量流体惯性力和压强合力的量级关系，不可压缩理想流体定常流动的能量积分可表示为

式中：p0为等熵滞止压强；U为流速。若考虑流体的可压缩性，式（15）可表示为

对比式（15）和（16）可知，当流场中最大马赫数小于0.3时，理想流体定常等熵流动可用不可压缩理想流体方程近似。当马赫数大于0.3 时，必须考虑流体的可压缩性［12］。本文研究的高速磁浮列车最大运行速度为600km·h-1，马赫数达到0.5左右，需要考虑流体的可压缩性。

面ABCD采用压力远场边界条件，大小为1 个标准大气压，当列车运行速度分别为300、430、500和600km·h-1时，对应马赫数分别为0.245、0.351、0.408和0.490。面EFGH采用压力出口边界条件，大小为1 个标准大气压。根据相对运动原理，假设磁浮列车在计算域中是静止的，轨道壁面和计算域底面向相反方向运动。为了消除边界层的影响，将地面CDHG和轨道表面设置为滑移壁面，与磁浮列车运行速度大小相同，方向相反。列车表面设置为无滑移固定壁面，面ADHE、BCGF和ABFE设置为对称边界条件。

2.3 网格划分

采用混合法进行网格单元划分，划分结果如图3所示。在靠近车体的区域采用四面体和三棱柱型非结构网格进行划分，最大网格尺寸不超过40mm。在距车体一定距离的计算域采用六面体结构型网格，按照一定的增长系数进行网格划分，最大网格尺寸不超过500mm。车体和轨道表面采用三角形网格划分，最大网格尺寸不超过15mm，为了更准确地模拟空气流动对车体表面的影响，对列车表面进行边界层网格划分，其中第1 层网格到壁面的法向距离为1mm，共5层边界层网格，网格增长率为1.2。

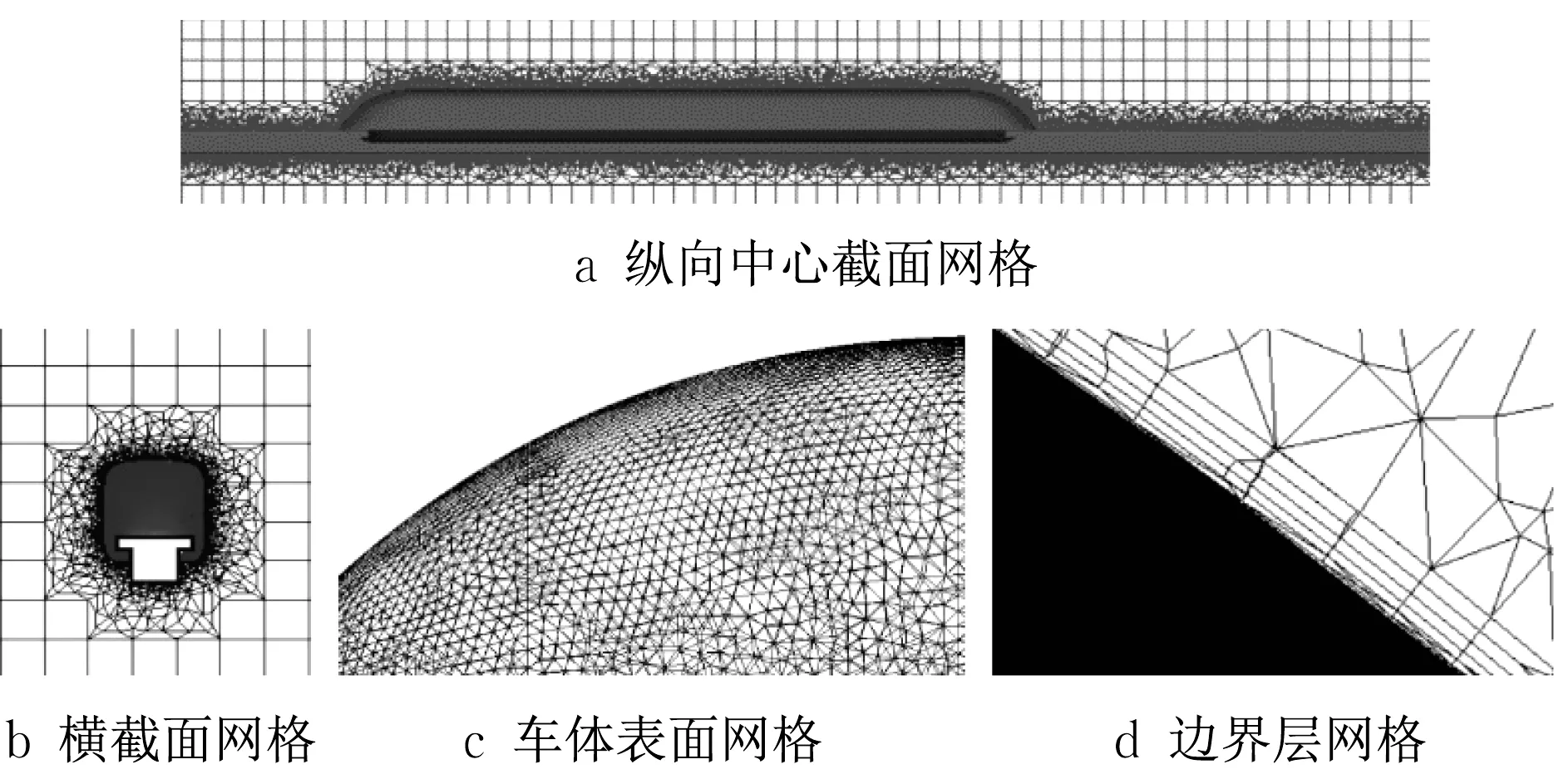
图3 高速磁浮列车网格示意Fig.3 Schematic diagram of grids of high-speed maglev train

2.4 计算方法

考虑流体的可压缩性，先进行稳态流场求解，将稳态流场的计算结果作为瞬态流场计算的初始值进行非稳态流场计算。瞬态流场计算采用基于SSTk-ω的DES模型，采用SIMPLE算法用于压力和速度耦合，连续性方程采用标准格式离散，动量方程采用有界中心差分格式离散，能量方程、湍动能方程和相对湍流耗散率方程采用二阶迎风格式离散，时间差分方程使用有界二阶隐式格式离散。瞬态流场计算的时间步长为Δt=0.000 1s，根据奈奎斯特采样定律，噪声的最大分析频率为fmax=1/（2Δt）=5 000Hz。瞬态流场共计算2 000 个时间步长，后1 000步记录每个时间步长的瞬时流场数据，总采样时间为0.1s，频率分辨率为10Hz。

3 高速磁浮列车流场特性分析

第3 节、第4 节研究的磁浮列车运行速度均为430km·h-1。图4 和图5 分别为磁浮列车表面静压分布云图和列车周围流体纵剖面速度分布云图。由图可知，头车鼻尖最先与气流接触，气流被鼻尖阻断，流速接近于零，鼻尖处静态压强达到最大值，约为8 885Pa。由于列车头部表面曲率变化较大，气流从鼻尖流向列车顶部、侧面和底部时速度加快，导致车头周围区域压强急剧下降，从正压转变为负压。当气流到达车头流线型肩部区域时，气体流速最快，负压达到峰值，约为−8 088Pa。车身表面大部分区域为绝对值较小的负压，由于车身表面比较平滑，压力梯度没有较大变化。列车尾部的压强分布与头车相似，由于能量耗散作用，列车尾部区域的压强绝对值均小于列车头部对应区域的压强绝对值。

图4 高速磁浮列车表面压力Fig.4 Contours of pressure at surface of highspeed maglev train

图5 列车周围流体纵剖面速率Fig.5 Contours of velocity at longitudinal section of fluid around train

湍动能反映列车表面脉动压力大小，可评估车体表面噪声源分布。由图6 可知，湍动能主要分布在头车表面及车头流线型肩部区域。尾部流线型肩部附近区域存在明显气流分离现象，该区域气体流速较小，湍动能较大。尾流区域存在一对旋转方向相反的2个尾涡，尾涡向后部区域延伸较长距离。

图6 列车表面及周围流体垂向截面湍动能Fig.6 Contours of turbulent kinetic energy at ver⁃tical section of train surface and surrounding fluid

4 高速磁浮列车气动噪声特性分析

4.1 近场声学特性

高速磁浮列车气动噪声是一种宽频带噪声，即没有明显的主频段，声能在较宽的频率范围内连续分布。基于稳态流场数据，利用宽带噪声源模型可计算由湍流边界层产生的列车表面单位面积气动噪声声功率［13］。图7 为列车表面声功率级分布云图。由图可知，车体表面声功率级最大值出现在头车和尾车流线型肩部区域。车身表面声功率级随列车纵向变化较小，因此缩短计算模型长度对车体表面噪声源分布影响较小。列车表面声功率级和流场湍动能具有相似的分布特性，可见高速磁浮列车主要噪声源分布区域为气流分离和湍流剧烈的区域。

图7 列车表面声功率级Fig.7 Contours of sound power level of train sur⁃face

基于Lighthill 声比拟理论，将用DES 模型计算得到的每个时间步长的瞬态流场数据转换为Lighthill 声源项，再对时域的声源项进行傅里叶变换，得到频域Lighthill 声源项。根据流场分析结果，建立包含主要声源区域在内的声学有限元－无限元模型，有限元区域设置为空气介质。将频域Lighthill声源插值映射到声学网格单元节点处，随后进行近场和远场声传播计算。

图8为声学有限元计算列车表面声压级测点布置示意，布置3个测点，P1与P2分别位于头车与尾车驾驶室挡风玻璃处，P3位于尾车侧窗处。图9 为运行速度为430km·h-1的磁浮列车车体表面3个测点的声压级1/3 倍频程频谱曲线图。由图可知，除个别频带外，头车和尾车驾驶室挡风玻璃处声压级高于尾车侧窗测点声压级。对于P3点，A 声级先随频率的增大而增大，在630Hz～3 150Hz频率范围内，A声级基本不随频率变化，约为120dB（A）；频率高于3 150Hz 时，A 声级随频率的增大而减小，P3点A 计权总声级为129.2dB（A）。当频率小于500Hz时，P2点比P1点声压级高；当频率大于500Hz时，P2点比P1点声压级低。因为磁浮列车在尾流区产生一对尺度较大的尾涡，其能量主要集中在低频，故尾车P2点低频声压级较大。根据流场计算结果可知，由于能量耗散作用，尾车附近湍动能比头车低，湍动能主要反映高频能量，故尾车测点P2的高频声压级较小。P1和P2点A计权总声级分别为141.2 和145.1dB（A）。

图8 列车表面声压级测点布置Fig.8 Layout of sound pressure measuring points on train surface

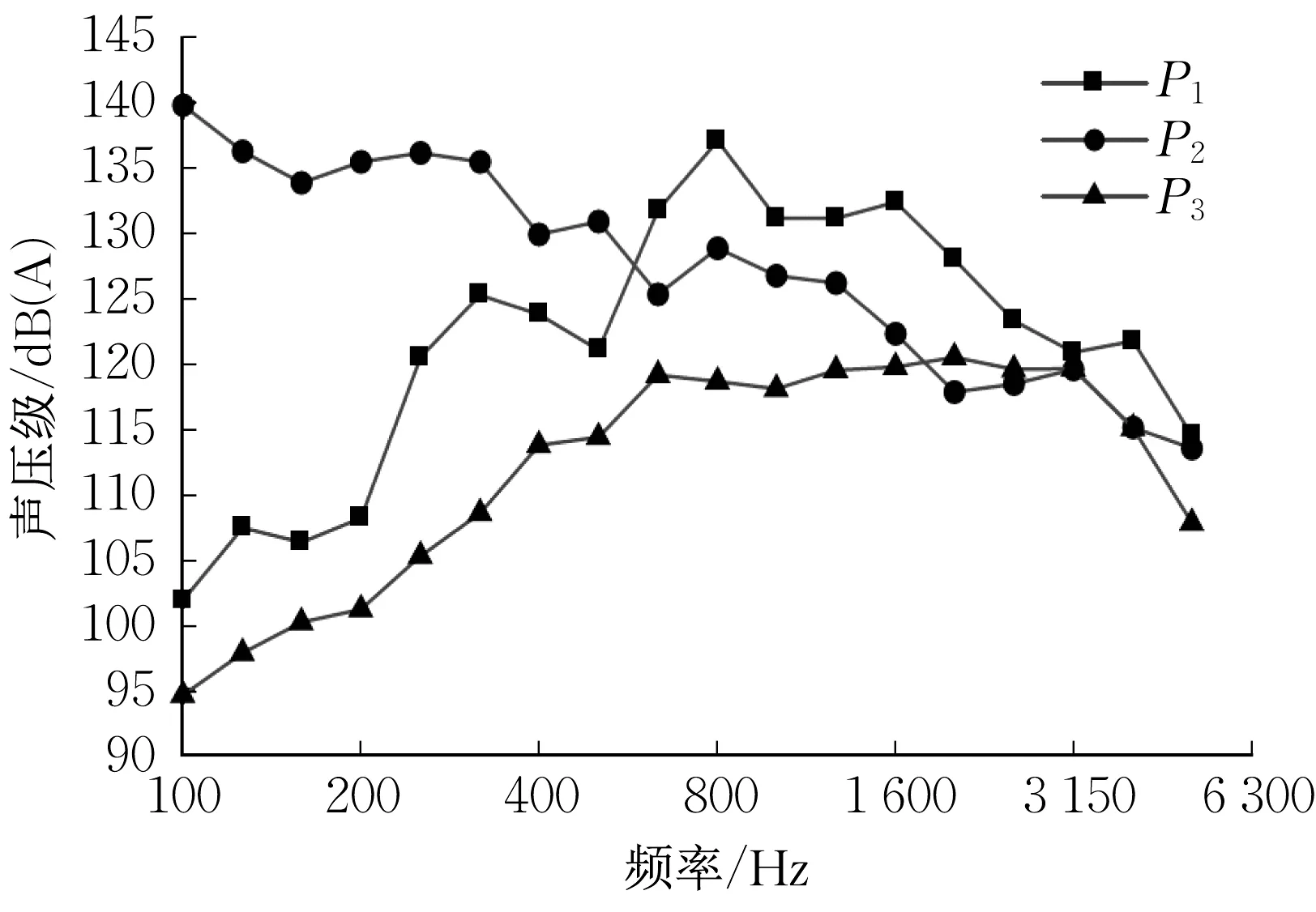
图9 车体表面测点声压级频谱曲线Fig.9 Frequency spectral of sound pressure of measuring points on train surface

4.2 远场声学特性

为研究高速磁浮列车远场气动噪声特性，参考国际标准ISO3095—2013在距离轨道中心线7.5m、轨面高度1.2m以及距离轨道中心线25m、轨面高度3.5m 位置沿列车纵向均匀布置2 列噪声测点，每列端部的2个测点分别与头车和尾车鼻尖处于同一横截面，远场噪声测点布置如图10所示，每2个相邻纵向测点的距离为1m，共110个测点。图11为列车运行速度为430km·h-1时距离轨道中心线7.5m、轨面高度1.2m 位置处沿列车纵向A 声级随距离分布曲线图，其中0m位置对应于2节车的连接处。由图可知，A声级沿列车纵向距离先增大后减小，尾车流线型区域总A声级大于头车流线型区域总A声级。纵向最大A 声级不是出现在0m 位置，而是更偏向尾车，大约在7m位置，声压级为106.9dB（A）。

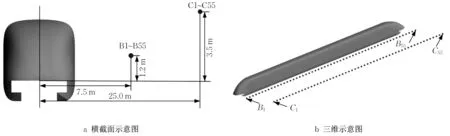
图10 远场气动噪声测点布置Fig.10 Layout of far-field aerodynamic noise measuring points

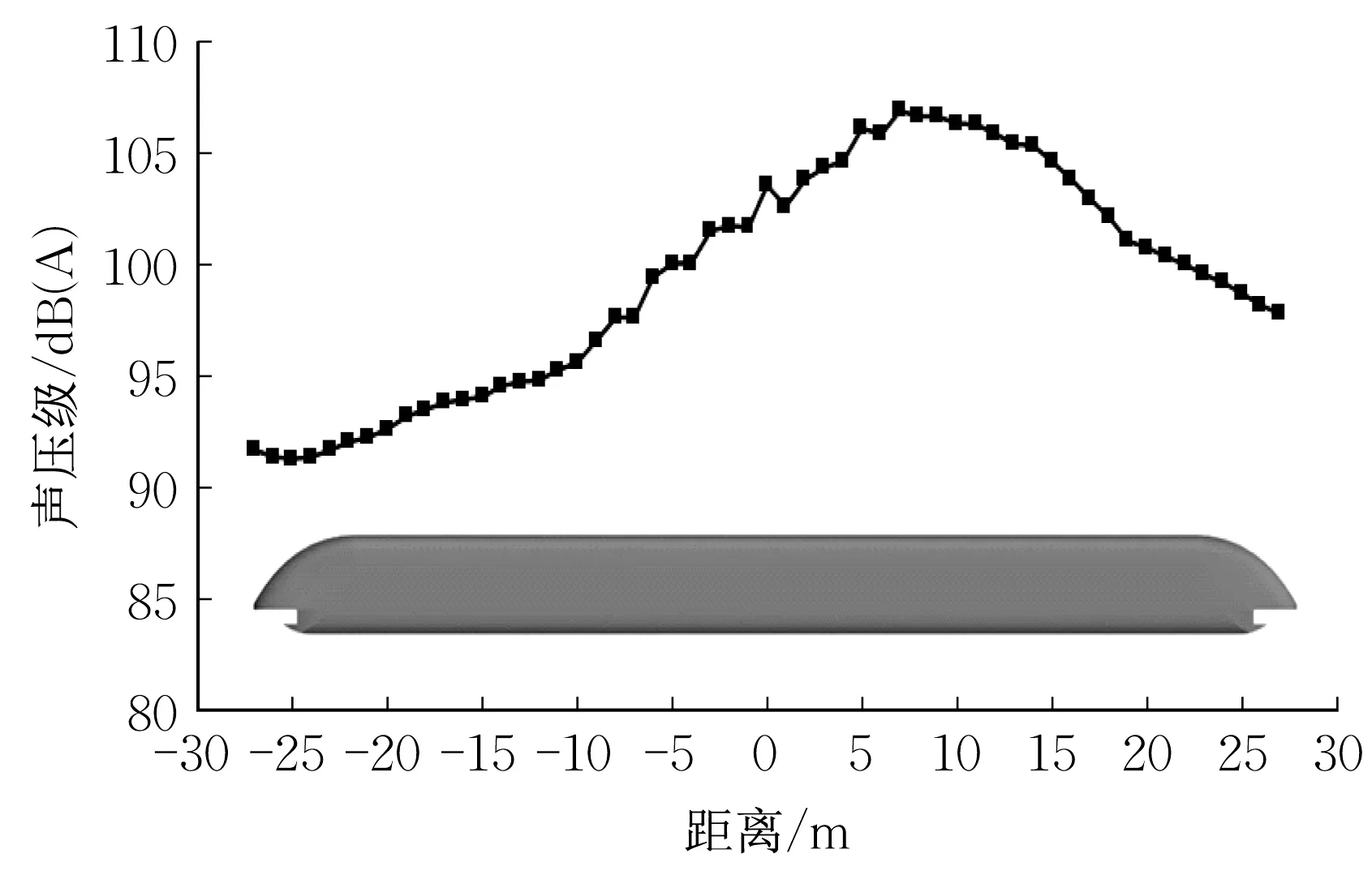
图11 A声级沿列车纵向分布曲线Fig.11 Curve of A-weighted sound pressure distri⁃bution along longitudinal direction of train

将每列噪声测点计算得到的A声级进行能量平均，可近似得到高速磁浮列车通过时间内等效连续A 声级频谱结果（图12）。由图可知，远场气动噪声是一种宽带噪声，当频率较低时，A声级随频率增大而增大，气动噪声的能量主要集中在中高频区域，为1 000～1 600Hz。距离轨道中心线7.5m、轨面高度1.2m处噪声峰值位于中心频率为1 250Hz的1/3倍频程频带内，为97.0dB（A）；距离轨道中心线25m、轨面高度3.5m处噪声峰值位于中心频率为1 600Hz的1/3倍频程频带内，为91.9dB（A）。在高频区域，7.5m 和25m 处噪声声压级差异较小；在中低频区域，各频带7.5m处声压级比25m处高2.7～8.9dB（A）。图13为500Hz和1 600Hz高速磁浮列车车外声场分布云图，选取的2 个截面分别为x=7m 横截面和轨面以上1.2m 截面。由图可知，在中低频范围内，车尾附近区域声压级高于车头对应区域，因为尾流区域存在大尺度尾涡，且向后延伸了较长的距离，可见涡是流体流动发声的声源。在高频范围内，声场分布比较混乱，车头区域声压级略高于车尾区域。

图12 远场噪声测点平均声压级频谱曲线Fig.12 Frequency spectral of average sound pres⁃sure at far-field noise measuring points

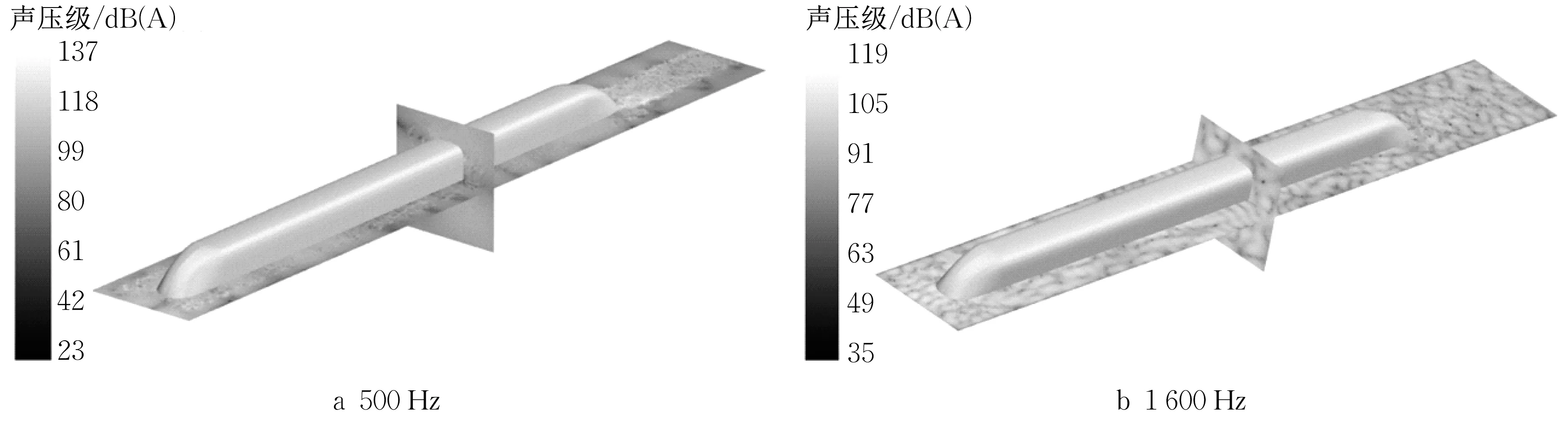
图13 列车车外声场分布Fig.13 Contours of sound field distribution outside train

5 试验验证与分析

为验证高速磁浮列车气动噪声计算模型的准确性，在上海龙阳—浦东磁浮线上对TR08 高速磁浮列车进行在线实车试验。列车运行速度为300、430km·h-1，共布置2 类测点。第1 类是在尾车车外侧窗处布置航空表面传声器，测点位置与图8 的P3测点位置相同。第2 类是在距离轨道中心线7.5m、轨面以上1.2m处以及距离轨道中心线25m、轨面以上3.5m处布置自由场传声器，用于测试高速磁浮列车通过噪声，图14为在线实车试验测试现场图。远场通过噪声测点位于同一横截面，周围无大的声反射体及其他噪声源。采用PLUSE Labshop 多通道声学测量系统进行测试，每个运行速度至少测量8组数据，将声压级测试结果取能量平均。图15为不同运行速度下高速磁浮列车车体表面噪声声压级试验与仿真1/3 倍频程频谱曲线对比图。由图可知，车体表面噪声能量主要集中在800～2 500Hz 范围内，当列车运行速度由300km·h-1增加到430km·h-1时，高频噪声比低频噪声的增长量大，频率低于2 000Hz 时，各频带声压级增大3～9dB（A），频率高于2 000Hz时，各频带声压级增大9～17dB（A），测点总声压级增大7.6dB（A）。除中心频率为5 000Hz的1/3 倍频程频带外，车体表面噪声声压级在各频带试验与仿真误差不超过3dB（A），且频谱曲线具有相似的变化趋势。

图14 实车试验现场Fig.14 Real vehicle test site

图15 车体表面试验与仿真噪声频谱对比Fig.15 Comparison of noise frequency spectrum on train surface between test and simulation

图16 为不同运行速度下高速磁浮列车通过时间内等效连续A声级试验与仿真1/3倍频程频谱曲线对比图。由图可知，当列车运行速度由300km·h-1增加到430km·h-1时，远场气动噪声峰值向高频方向移动，7.5m 和25m 处总A 声级分别增大5.1dB（A）和6.4dB（A）。远场噪声声压级在各频带试验与仿真误差不超过4dB（A），且频谱曲线具有相似变化趋势，运行速度为300km·h-1时，7.5m和25m处总A声级试验与仿真误差分别为2.7dB（A）和1.7dB（A）；运行速度为430km·h-1时，7.5m 和25m 处总A 声级试验与仿真误差分别为0.4dB（A）和0.1dB（A）。证明高速磁浮列车流场和声学仿真计算结果准确性较高，模型可用于预测更高运行速度的气动噪声。

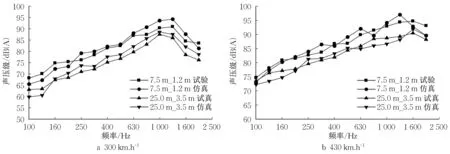
图16 远场试验与仿真频谱对比Fig.16 Comparison of far-field noise frequency spectrum between test and simulation

6 高速磁浮列车车外噪声预测

进行运行速度分别为300、430、500和600km·h-1的高速磁浮列车车外气动噪声计算，计算得到各速度下尾车车体表面侧窗处总A声级以及距离轨道中心线7.5m、轨面以上1.2m 处和距离轨道中心线25m、轨面以上3.5m 处列车通过时间内等效连续A声级。参考高速列车A 声级与速度的关系［1］，不同速度下A声级可以用速度修正量进行表达，表示为

式中：v为列车运行速度；Lp为运行速度v时总A 声级；v0为参考速度，取300km·h-1；Lp0为参考速度v0下总A 声级；k为速度修正系数。图17 为高速磁浮列车不同位置总A 声级随速度关系曲线图，图中虚线为拟合回归线。

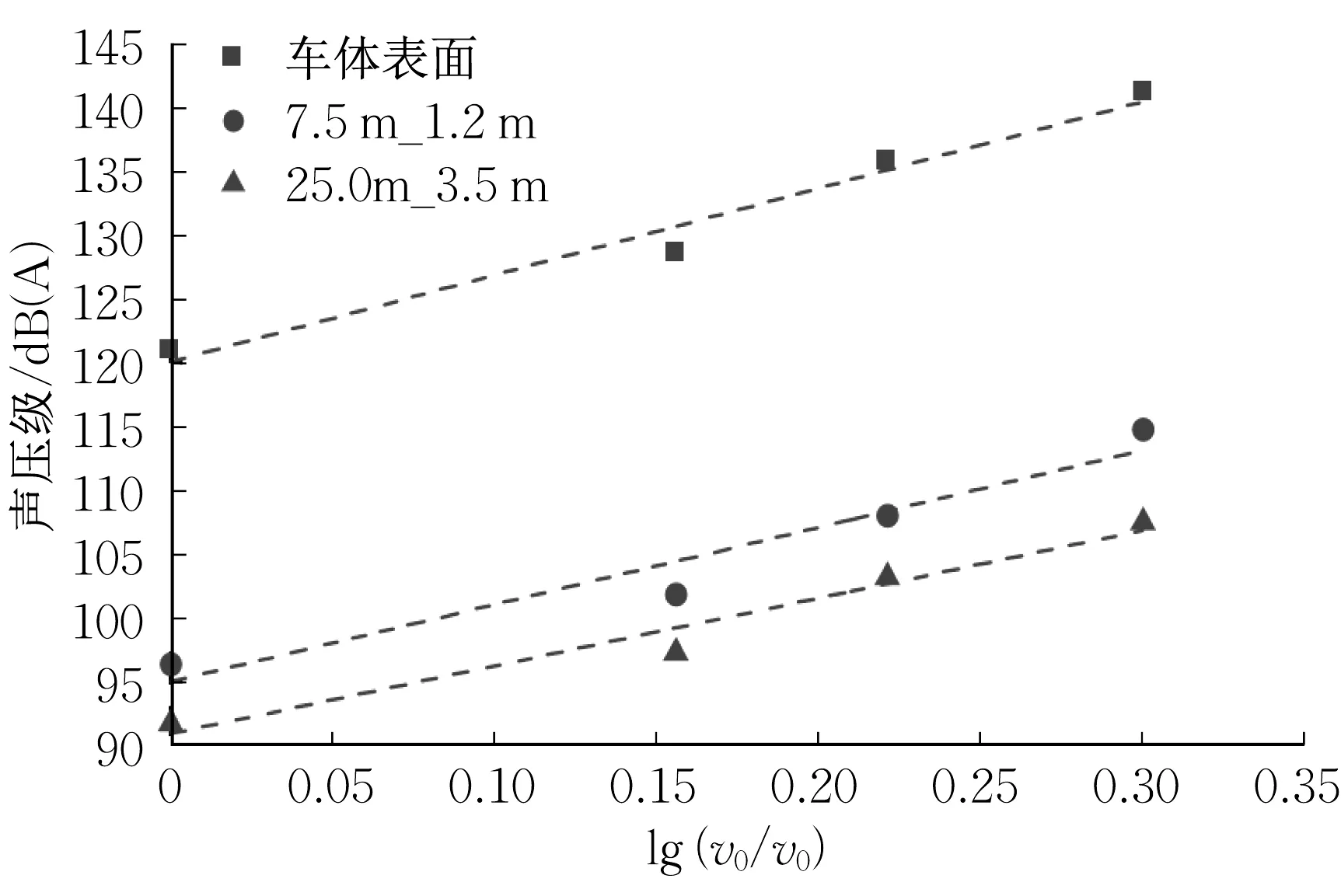
图17 总A声级随速度关系Fig.17 Total A-weighted sound pressure versus speed

尾车车体表面侧窗处总A声级与速度拟合得到的函数关系为

距离轨道中心线7.5m、轨面以上1.2m 位置处磁浮列车通过时间内等效连续A声级与速度拟合得到的函数关系为

距离轨道中心线25m、轨面以上3.5m位置处磁浮列车通过时间内等效连续A声级与速度拟合得到的函数关系为

所有拟合的决定系数R2均大于0.94，可见用对数拟合高速磁浮列车不同位置总A声级随速度的变化关系比较准确。速度修正系数k在车体表面值最大，为67.8，由于偶极子和四极子声源的辐射声功率分别与流体流速的6次方和8次方成正比，对应的速度修正系数分别为60和80，因此高速磁浮列车气动噪声声源为包含偶极子声源和四极子声源的混合声源。随着测点位置距离磁浮列车表面越来越远，速度修正系数k的值也不断减小，在距离轨道中心线25 m、轨面以上3.5 m 处，当列车运行速度分别为500 km·h-1和600 km·h-1时，通过时间内等效连续A声级分别为103.2 dB（A）和107.5 dB（A）。

图18为500 km·h-1和600 km·h-1运行速度下，距离轨道中心线25 m、轨面以上3.5 m 测点处列车通过时间内等效连续A 声级1/3 倍频程频谱曲线图。由图可知，远场气动噪声的能量主要集中在中高频区域，大约在800 Hz 到2 000 Hz 之间。运行速度分别为500 km·h-1和600 km·h-1时，噪声峰值均位于中心频率为1 600 Hz 的1/3 倍频程频带内，分别为96.5 dB（A）和101.9 dB（A）。当列车运行速度由500 km·h-1增加到600 km·h-1时，在100～200 Hz 的低频区域，噪声声压级增长量较小，约为1～2 dB（A）；在250 Hz 以上的中高频区域，噪声声压级增长量较大，约为2.5～5.5 dB（A）。

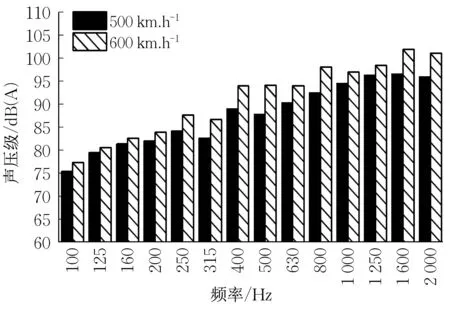
图18 更高速度远场噪声频谱预测Fig.18 Prediction of far-field noise frequency spec⁃trum at higher speeds

随着磁浮列车运行速度的增加，车外远场气动噪声会显著增大，过大的通过噪声会严重影响沿线居民的日常生活。为降低车外噪声，可以考虑优化车身外表面形状、安装半封闭或全封闭声屏障等措施降低噪声。

7 结论

建立了TR08 高速磁浮列车及桥梁的几何模型，采用分离涡模拟（DES）计算列车周围瞬态流场，利用宽带噪声源模型分析列车表面噪声源强度，基于Lighthill 声比拟理论和声学有限元方法进行气动噪声计算。通过对比高速磁浮列车在线实车试验数据与数值仿真数据，验证了数值计算模型的准确性，并得到了以下结论：

（1）高速磁浮列车车外气动噪声是一种宽频带噪声，主要噪声源分布区域为头车和尾车流线型肩部等气流分离及湍流剧烈的区域，缩短计算模型长度对车体表面噪声源分布的影响较小。

（2）对于车体表面噪声，除个别频带外，头车和尾车驾驶室挡风玻璃处声压级高于尾车侧窗。受到尾流区大尺度尾涡及能量耗散的影响，在频率小于500 Hz 的低频区域，头车驾驶室挡风玻璃处声压级比尾车对应位置小；频率大于500 Hz的中高频区域，头车驾驶室挡风玻璃处声压级比尾车对应位置大。

（3）对于远场气动噪声，在距离轨道中心线7.5m、轨面高度1.2 m处，A声级沿列车纵向先增大后减小，尾车流线型区域总A 声级大于对应头车流线型区域总A 声级，最大A 声级所在位置更偏向尾车。远场气动噪声的能量集中在1 000 Hz到1 600 Hz之间的中高频区域，在中低频范围内，车尾附近区域声压级高于车头对应区域；在高频范围内，声场分布比较复杂，车头区域声压级略高于车尾区域。

（4）车体表面噪声及远场通过时间内等效连续A 声级与列车运行速度呈对数变化关系，速度修正系数k随测点位置离列车距离的增大而减小。随着列车运行速度的增加，远场气动噪声能量向高频移动。当列车运行速度为600 km·h-1时，距离轨道中心线25 m、轨面以上3.5 m 位置处列车通过时间内等效连续A 声级达到107.5 dB（A），噪声峰值位于中心频率为1 600 Hz 的1/3 倍频程频带内，为101.9 dB（A），未来可通过优化车身外表面形状、安装半封闭或全封闭声屏障等措施降低噪声。

作者贡献声明：

陈雨豪：文献调研，模型建立，仿真计算，数据分析，论文写作与修改。

葛剑敏：指导论文思路，设计试验方案，参与论文修订。

丁叁叁：参与研究的构思与设计。

朱雷威：参与试验数据的测试与分析。

郭建强：参与试验数据的测试与分析。