高机动水下航行体运动控制技术研究

李明华，权晓波，魏海鹏，王凡瑜

高机动水下航行体运动控制技术研究

李明华1，权晓波1，魏海鹏2，王凡瑜2

（1. 中国运载火箭技术研究院，北京，100076；2. 北京宇航系统工程研究所，北京，100076）

针对航行体水下高机动运动控制问题，建立基于水下航行体动力学方程的六自由度数学仿真模型，分析控制力和推进力对航行体水下机动过程的影响，提出小攻角机动和大攻角漂移机动两种弹道模式。仿真结果表明，实现小攻角机动控制力需求大，航行体运动速度高；漂移机动模式能够大幅降低控制力需求，弹道参数及稳定性受航行体运动速度影响显著，尽可能晚地施加推进力有利于姿态稳定控制，但航行体运动速度衰减较大。通过开展航行体水下机动实航试验，验证和确认了漂移机动模式的工程可实现性。

水下机动；运动控制；机动模式；小攻角机动；漂移机动

0 引 言

水下航行体是重要的海上装备，近年来相关领域对其提出了执行多样化任务的新需求，要求其机动性能等关键指标不断提升，其中高机动性、高稳定性是工程研制的难点问题之一。

水下运动控制技术属于飞行力学、流体力学、自动控制等多学科多专业的交叉领域。与空中飞行相比，水介质的密度比空气高800倍左右，航行体水下运动所受流体动力量值大、非线性和非定常特征强，对航行速度和攻角更加敏感，另一方面浮力、阻尼力、附加惯性力及其与重力的耦合影响不可忽略。上述动力学特征导致质心运动与绕心旋转运动关联性强，空中飞行惯用的弹道与姿态稳定控制理论和工程设计方法在水下机动问题中的适用性尚未确认。

关于水下航行体运动控制问题的研究，国内外已有一定研究积累：荣建德等[1]研究了快衰减运动稳定性设计准则，丁彦超等[2]研究了垂直出水过程推力矢量最优控制理论。现有研究集中于小曲率机动问题，对米级转弯半径的水下高性能机动过程讨论较少，与水下航行体工程研制需求存在一定差距。

针对水下航行体高性能机动过程运动控制面临的问题，本文分析了分析小攻角机动和大攻角漂移机动两种弹道模式的运动特性，重点讨论了推进力施加时机对漂移机动弹道的影响，并通过实航试验确认了漂移机动模式的工程可实现性。

1 数学模型

1.1 坐标系定义

1.2 动力学建模

为简化附加质量的计算，在随体坐标系下展开动量（矩）定理，并考虑试验获取的水动力系数蕴含部分惯性力项[3]，整理得到航行体水下运动的动力学方程：

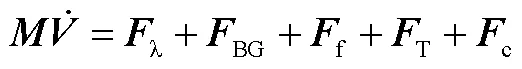
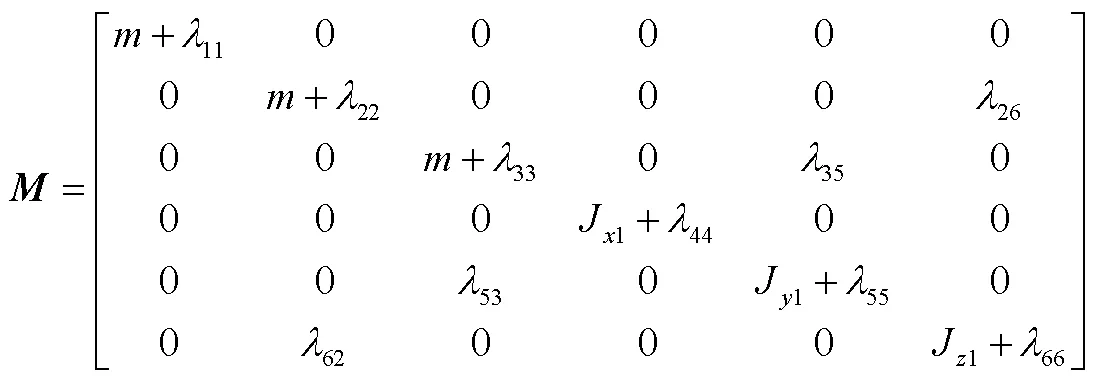
采用Dormand-Prince算法[5]，分轴向通道、法向-俯仰通道、横向-偏航通道和滚转通道显式推进求解（角）加速度，进而通过积分和坐标变换解算其他弹道参数。为增强数值稳定性，在航行体质量、转动惯量等参数随时间变化的情况下，采用固定时间步长的4阶Runge-Kutta方法[6]推进求解。

2 航行体水下机动模式研究

当航行体总体方案确定后，质量、转动惯量、浮力、浮心等可控制在一定范围内，由式（1）可知，控制力和推进力决定了航行体的运动过程和机动性能。因此保持初始运动速度、推进力量值等其他条件相同，改变控制力大小和推进力施加时刻，研究不同工况下航行体运动规律和机动性能。采用比例-微分控制律[7]操纵典型水下航行体机动变向，开展了多工况机动弹道仿真计算，如表1所示。

表1 典型水下航行体机动弹道仿真计算工况

Tab.1 Simulation Conditions of Typical Underwater Vehicle Maneuver Trajectories

序号许用控制力推进力施加时刻 1 2 3 4

不同工况下的航行体水下运动仿真结果如图1所示。由图1可知，工况1机动弹道明显偏离期望航向，速度剧烈波动、攻角发散，无法实现稳定的机动变向；工况2、3、4中航行体均能实现稳定的机动变向。在控制力较大的情况下，工况3机动过程攻角小、运动速度高，但弹道曲率小、转弯半径大；在施加推进力较晚的情况下，工况2和工况4机动过程中攻角大，运动速度先降低后升高，弹道曲率大，机动转向半径小。

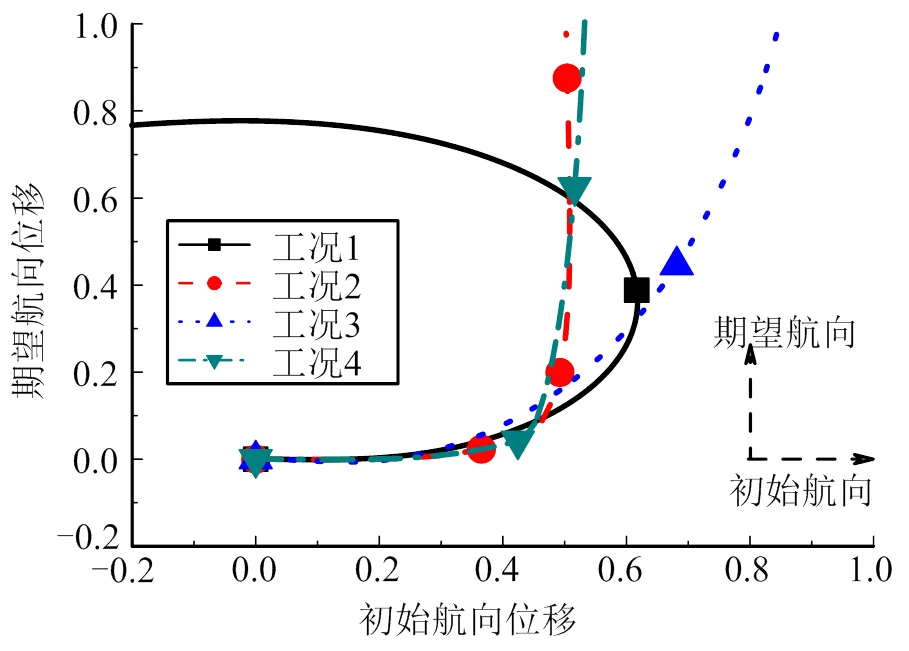
a）运动轨迹

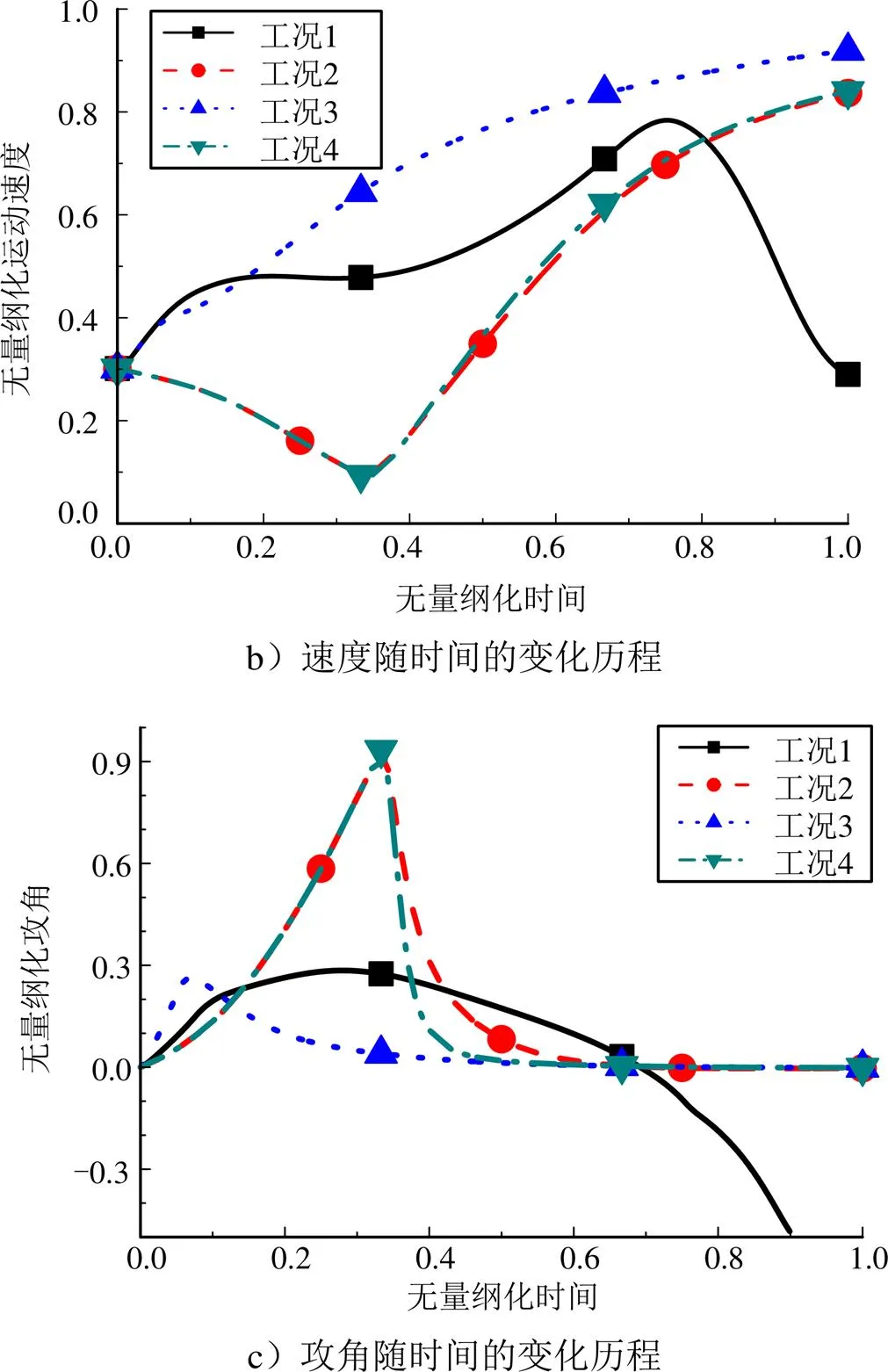
续图1

根据上述运动特点，将与工况3类似的机动模式称为小攻角机动，工况2和工况4机动过程与车辆、船舶等甩尾过弯[8]具有一定相似性，故将该机动模式称为漂移机动。两种机动模式的适用情形和运动特点如表2所示。

表2 小攻角机动和漂移机动的适用情形及运动特点

Tab.2 Applicability and Motion Characteristics of Low-attack-angle Maneuver and Drift Maneuver

机动模式小攻角机动漂移机动 控制力需求高低 施加推进力早晚 运动攻角小大 运动速度快慢 转弯半径大小

3 航行体水下小攻角机动的实现条件

小攻角机动模式如图2所示，由图2可知，航行体转向过程中速度大小几乎不变，姿态随速度方向同步变化至期望航向，保持较小的运动攻角。攻角是影响水下航行体所受流体动力的重要因素，当航行体做小攻角机动时，动力学方程可以通过摄动展开舍去高阶项进行简化，从而使航行体运动模型成为线性系统，为理论研究和工程实践提供了方便[9]。

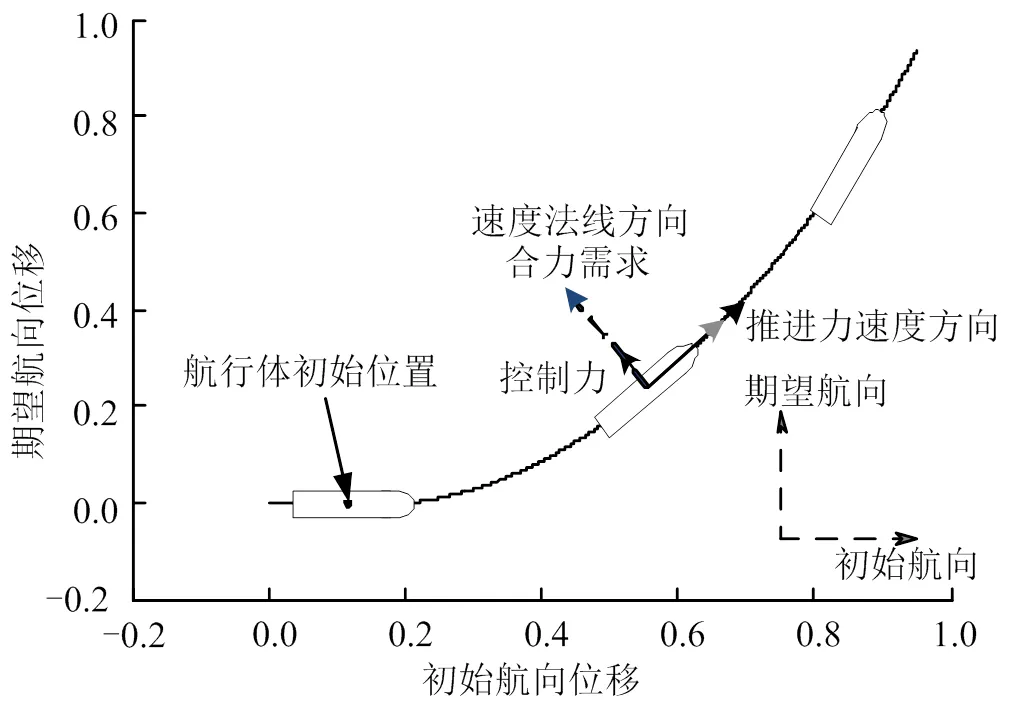
图2 小攻角机动弹道示意

航行体姿态与速度方向同步变化是小攻角机动模式的重要特征和前提条件，其核心在于质点弹道曲率与姿态控制能力相匹配。

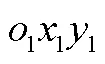
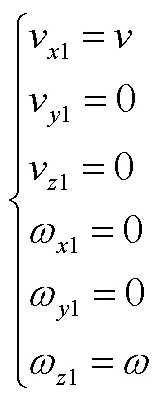
移项整理得，推进力需求为

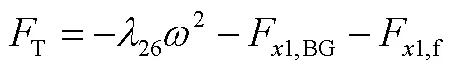
法向控制力需求为

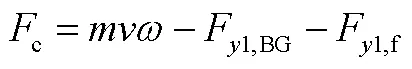
姿态控制力矩需求为

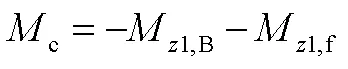
基于某航行体衡重特性，采用式（4）至式（6）反算得到，不同机动角速度对法向力和姿态控制力矩的匹配需求如图3所示。由图3可知，随机动角速度增大，控制力需求显著增加，而姿态控制力矩需求变化较缓慢。由式（5）、式（6）可知，控制力和控制力矩均起平衡净浮力（矩）和流体动力（矩）的作用，但控制力还需提供向心加速度，所以控制力需求对机动角速度更加敏感。

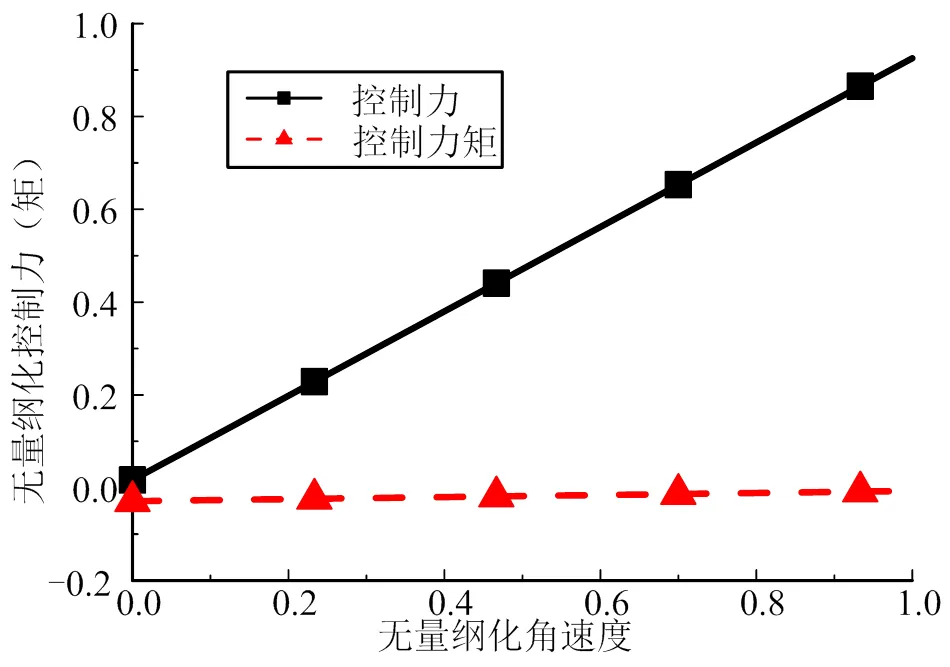
图3 不同机动角速度对控制力和控制力矩的匹配需求

当采用一套控制装置同时提供控制力和控制力矩时，等效作用点与航行体质心的距离为

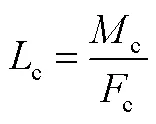
根据图3所示结果计算得到，随机动角速度增大，控制力等效作用点逐渐由航行体艉部向质心移动，采用小攻角模式实现高性能机动存在一定困难。

4 航行体水下漂移机动特性分析

4.1 控制力需求分析

漂移机动分为2个阶段：第一阶段调整姿态，使航行体轴线与速度方向相互垂直；第二阶段开始施加推进力，用于补充法向控制力从而改变速度方向。如图4所示，在调姿过程中，航行体运动速度的方向几乎不变。至航行体轴线方向与速度方向接近垂直时，通过推进力迅速改变速度方向。

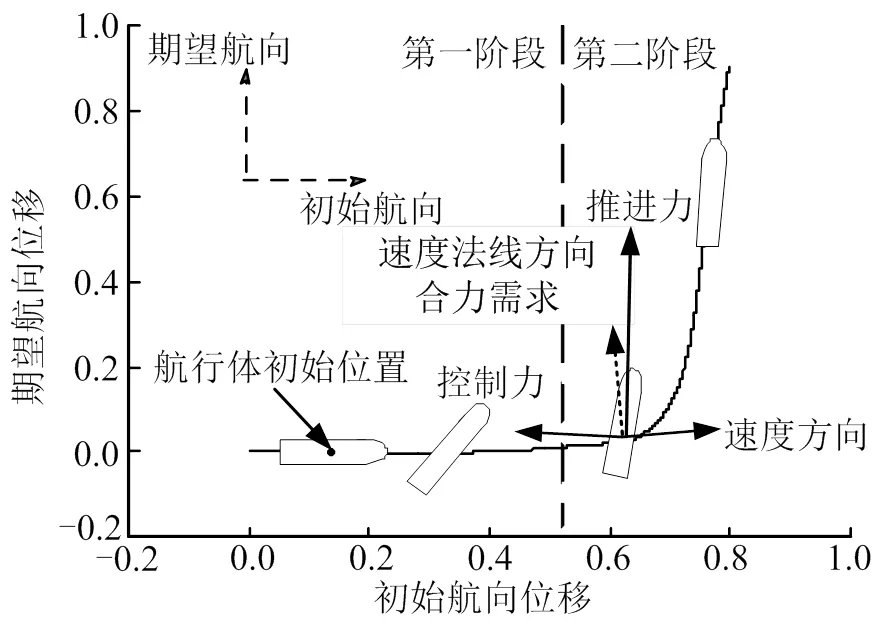
图4 漂移机动模式示意

采用漂移机动模式时，改变速度方向的法向力主要由推进力提供，控制力需求相比小攻角机动模式降低约80%，如图5所示。此时即使控制装置远离质心布置，也能够同时产生与需求接近的法向控制力和姿态控制力矩。

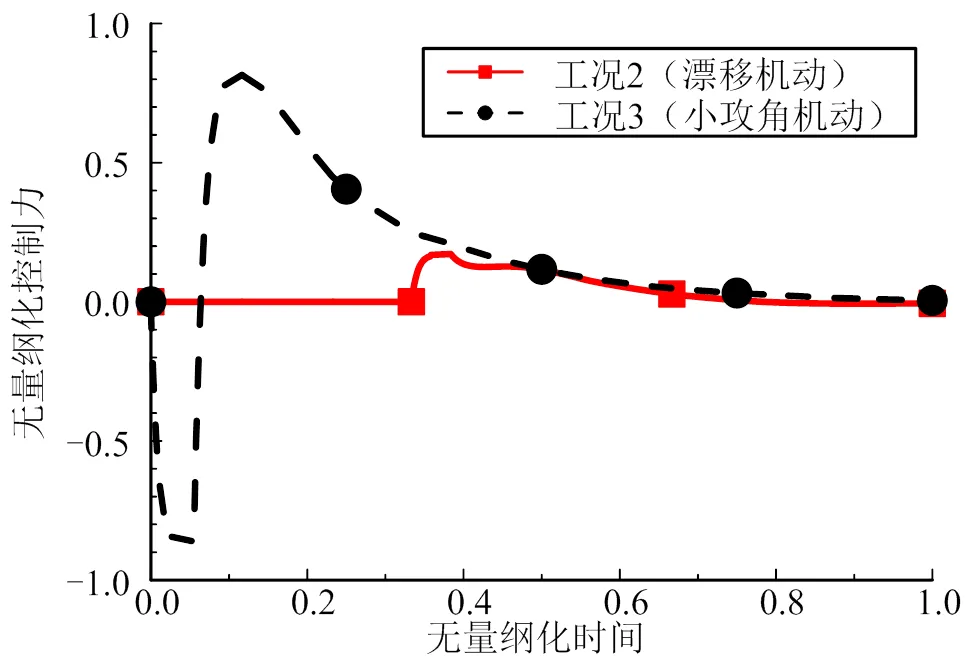
图5 漂移机动与小攻角机动的控制力需求对比

综上所述，漂移机动对法向控制力的需求较低，有利于控制装置布局，但机动过程中需要调整姿态使航行体轴线与速度方向接近垂直，运动攻角较大，流体动力很可能引入较强的非线性时变特征，动稳定性、对偏差和干扰的适应性等问题值得进一步研究分析。

4.2 推进力施加时刻影响分析

施加推进力的时机对漂移机动过程影响显著。对典型水下航行体，基于工况1的初边值条件，采用六自由度数学仿真模型研究推进力施加时机对漂移机动稳定性的影响，补充工况如表3所示。

表3 典型水下航行体机动弹道仿真计算工况（补充）

Tab.3 Simulation Conditions of Typical Underwater VehicleManeuver Trajectories (Additional)

序号许用控制力推进力施加时刻 1 5 6

3种工况下的机动弹道仿真计算结果如图6所示。由机动弹道末端切线与期望航向的偏差可以看出，越早施加推进力改变速度方向，机动过程的动稳定性越弱，机动弹道与期望航向的偏差越大。但施加推进力过晚（如工况6），航行体速度衰减量大，轴向速度衰减至零附近，不符合工程设计期望。

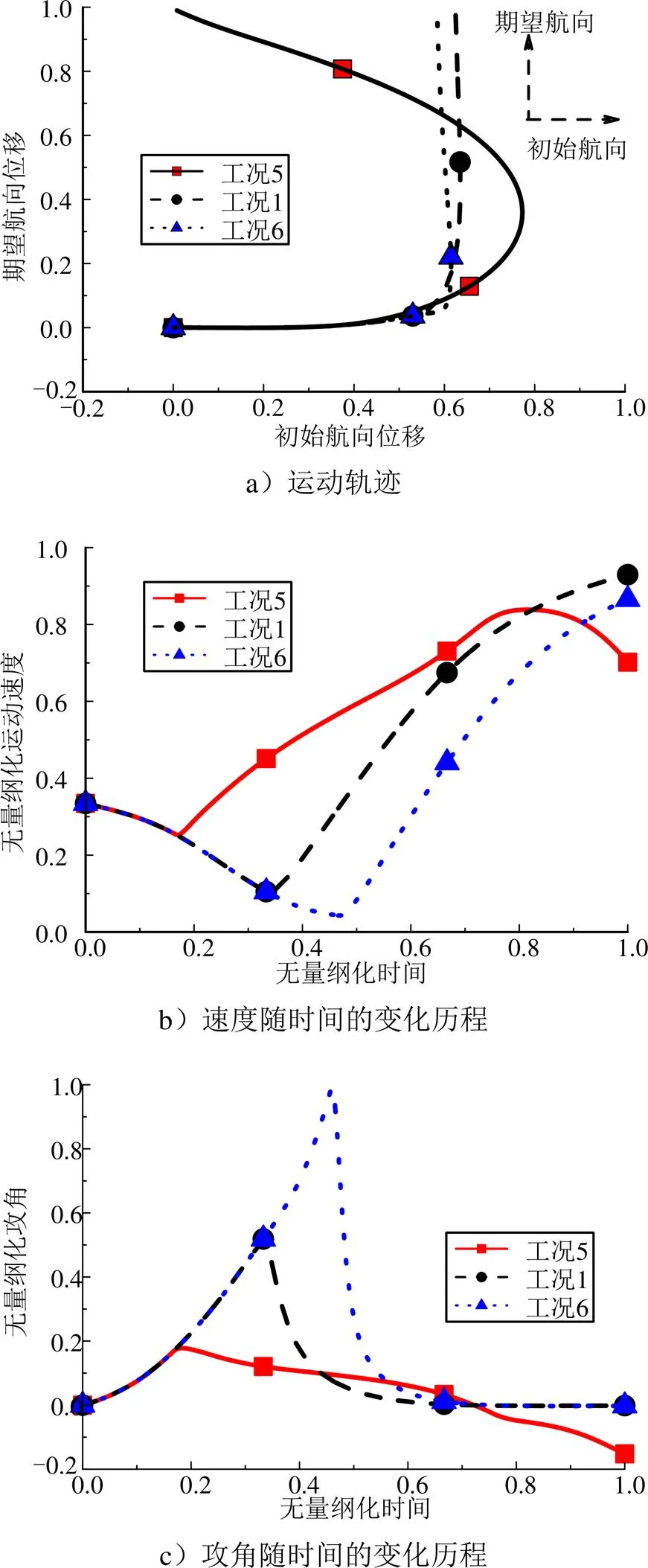
图6 不同推进力施加时刻的漂移机动仿真计算结果

动稳定性问题的本质在于控制力矩能否克抑制姿态及姿态角速度发散。航行体所受干扰力矩由浮力矩和水动力矩组成，其中水动力矩与运动速度的平方近似呈正比。越早施加推进力，同一时刻航行体运动速度更快，流体动力产生的干扰力矩越大，越不利于姿态稳定控制。

4.3 影响因素灵敏度分析

影响航行体水下运动的因素主要包括初始条件散布、航行体衡重特性偏差、水动特性偏差、控制力偏差、波浪干扰等。在工况1和工况5的基础上，考虑工程上易于实现的散布范围，分别叠加各项影响因素偏差开展机动弹道仿真计算。

以机动后航行方向为特征参数，分析各项影响因素灵敏度，结果如表4所示。由表4可知，工况1施加推进力较晚，各因素对航向的影响量普遍小于工况5，对偏差和干扰的适应能力较强，说明实施漂移机动时较晚施加推进力具有较好的稳健性。

表4 漂移机动影响因素灵敏度分析

Tab.4 Factor Sensitivity Analyze of Drift Maneuver

影响因素散布范围无量纲化航向影响量 工况1工况5 初始运动速度±15%0.1520.601 质量±2%0.0130.267 转动惯量±10%0.0200.106 水动特性±10%0.0834.364 控制力±10%0.0360.547 波浪波高2.5m0.1340.864

由于流体动力引入的干扰力矩随航行体运动速度平方增大，当施加推进力较晚时，初始运动速度散布对航向影响较大；当施加推力较早时，水动特性偏差对航向的影响力急剧增大。质量、转动惯量属于航行体的固有属性，工程上易于控制，其散布对漂移机动弹道特性影响较小。

5 航行体水下机动实航验证

为检验和确认漂移机动的可实现性，开展了航行体实航试验，数学仿真结果与试验数据的对比如图7所示。航行体在试验中完成了预期的机动动作，由图7可知，基于动力学模型的数学仿真结果与试验数据吻合良好，有效验证了本文关于漂移机动的研究和讨论。

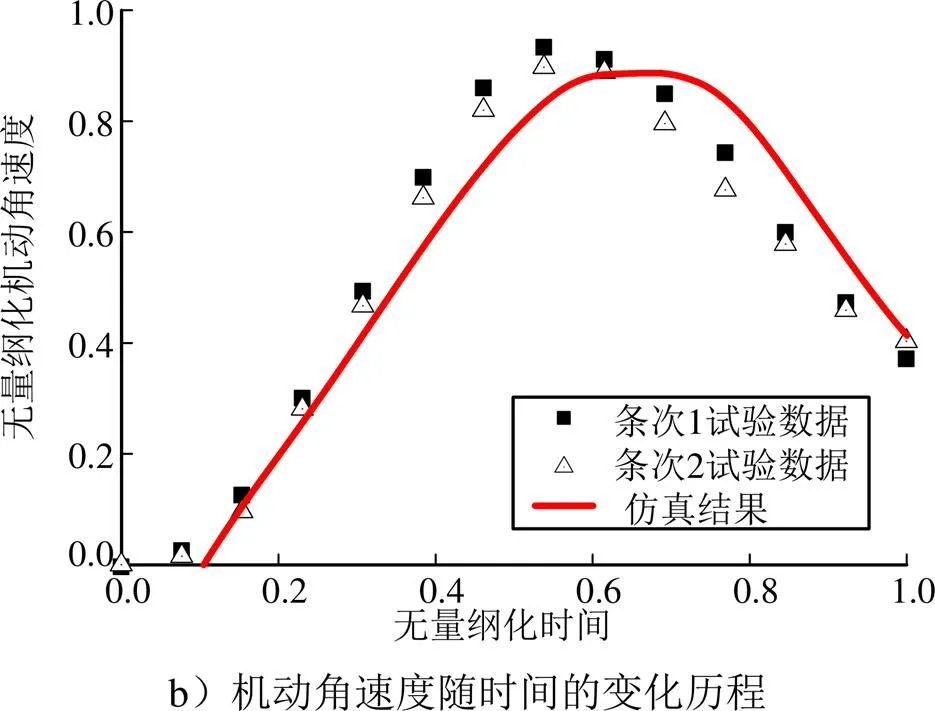
续图7

6 结 论

本文基于航行体水下运动六自由度动力学仿真模型，分析了控制力和推进力影响水下机动过程弹道特性的规律和机理，提出了小攻角机动与大攻角漂移机动两种模式，并通过实航试验确认了漂移机动的可实现性。研究表明：

a）小攻角机动运动速度较快，但控制力需求较高，并要求控制力与姿态控制力矩相匹配，其等效作用点随机动角速度提高逐渐向质心移动；

b）大攻角漂移机动模式的速度衰减量较大，但控制力需求大幅降低，控制力等效作用点可以远离质心，有利于姿态稳定和控制装置布局；

c）航行体运动速度通过改变干扰力矩量值显著影响漂移机动弹道及其稳定性，推进力施加时机需要考虑姿态稳定控制和偏差干扰适应能力联合优化。

[1] 荣建德. 水下运载器性能的分析与设计[M]. 北京: 国防工业出版社, 2008.

Rong Jiande. Analysis and design of performance of underwater launched capsules[M]. Beijing: National Defense Industry Press, 2008.

[2] 丁彦超, 王宝寿. 垂直潜射导弹推力矢量控制弹道仿真研究[J]. 船舶力学, 2011, 2(15): 87-94.

Ding yanchao, Wang Baoshou. Study on the thrust vector control trajectory of underwater vertical launching missile[J]. Journal of Ship Mechanics, 2011, 2(15): 87-94.

[3] 黄寿康. 流体动力·弹道·载荷·环境[M]. 北京: 宇航出版社, 1991.

Huang Shoukang. Hydrokinetics ballistic trajectory load environment[M]. Beijing: Space Navigation Publishing Company,1991.

[4] 严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.

Yan Weisheng. Torpedo navigation mechanics[M]. Xi’an: Northwestern Polytechnical University Press, 2005.

[5] Burden R L, Faires J D. 数值分析（第七版）[M]. 冯烟利, 朱海燕译. 北京: 高等教育出版社, 2005.

Burden R L, Faires J D. Numerical analysis (7th Edition)[M]. Feng Yanli, Zhu Haiyan Trans. Beijing: Higher Education Press, 2005.

[6] 李庆扬, 王能超, 易大义. 数值分析（第5版）[M]. 北京: 清华大学出版社, 2008.

Li Qingyang, Wang Nengchao, Yi Dayi. Numerical analysis (5th edition)[M]. Beijing: Tsinghua University Publishing House, 2008.

[7] 胡寿松. 自动控制原理（第七版）[M]. 北京: 科学出版社, 2019.

Hu Shousong. Automatic control principle (7th edition)[M]. Beijing: Science Press, 2009.

[8] 张放. 极限工况下自动驾驶车辆的轨迹规划与运动控制[D]. 北京: 清华大学, 2018.

Zhang Fang. Trajectory planning and motion control for extreme maneuvers of autonomous vehicles[D]. Beijing: Tsinghua University, 2018.

[9] 钱学森. 工程控制论（新世纪版）[M]. 戴汝为, 何善堉译. 上海: 上海交通大学出版社, 2007.

H S Tsien. Engineering cybernetics (New Century Edition)[M]. Dai Ruwei, He Shanyu Trans. Shanghai: Jiao Tong Universiy Press, 2007.

Study on Motion Control Technology of High-maneuverabilityUnderwater Vehicle

Li Ming-hua1, Quan Xiao-bo1, Wei Hai-peng2, Wang Fan-yu2

(1. China Academy of Launch Vehicle Technology, Beijing, 100076; 2. Beijing Institute of Astronautical System Engineering, Beijing, 100076)

To tackle motion control problems of high-maneuverability underwater vehicle, a six degree-of-freedom numerical simulation model is established based on the dynamic equation of underwater vehicles. Analyzing the effects of control force and propulsion force on the underwater maneuver, two patterns low-attack-angle maneuver and drift maneuver are proposed. Simulation results indicate that underwater vehicles maneuver faster with low-attack-angle pattern at cost of greater control force requisite. Lower control force is required when adapting drift maneuver pattern, while of greater velocity loss. When underwater vehicles execute drift maneuver, exploiting propulsion force as late as possible contributes to attitude stability control, as trajectory and stability are significantly affected by vehicle velocity. The engineering realization of drift maneuver pattern is verified and confirmed by underwater experiments.

underwater maneuver; motion control; maneuver pattern; low-attack-angle maneuver; drift maneuver

2097-1974(2023)01-0001-06

10.7654/j.issn.2097-1974.20230101

TP601

A

2023-02-07；

2023-02-09

国家自然科学基金项目（U20B2004）

李明华（1962-），男，研究员，主要研究方向为航天飞行器设计与控制、工程管理。

权晓波（1976-），男，博士，研究员，主要研究方向为飞行器总体设计。

魏海鹏（1982-），男，研究员，主要研究方向为飞行器总体设计。

王凡瑜（1996-），男，工程师，主要研究方向为跨介质航行体出水动力学。