基于Gauss伪谱法的高空飞行器再入段轨迹优化对传热效应的影响分析
邵嘉健,薛鹏飞
基于Gauss伪谱法的高空飞行器再入段轨迹优化对传热效应的影响分析
邵嘉健,薛鹏飞
(空间物理重点实验室,北京,100076)
基于Gauss伪谱法和二阶有限差分(Gauss Pseudospectral Method,GPM),研究了再入过程中高速飞行器的传热问题,并依据最内温层升温最小的目的进行飞行轨迹的数值优化。主要思路:构造传热分析模型,并依据传热方程构造每一温层的传热微分方程;将各温层微分方程以及动力学微分方程作为伪谱法中的微分方程约束条件代入,进行轨迹数值优化设计;利用少量LG点构造拉格朗日多项式,再通过一维插值获得大量LG点的值,获得更高精度的拟合结果曲线。以某高超声速飞行器为对象用本方法进行数值计算,结果验证了方法具有一定的可行性。
Gauss伪谱法;传热分析模型;轨迹优化设计
0 引 言
在飞行器气动加热的过程中,会影响乘员舱壳体温度的因素有两个:防隔热层材料及厚度以及飞行器由于气动加热形成的表面热流。而表面热流的形成与飞行器飞行模式密切相关,本文的研究内容便围绕弹道优化设计对飞行器壳体加热的影响展开[1,2]。
为实现本文对高速飞行器再入轨迹快速优化分析的目的,拟利用Gauss伪谱方法展开研究。Gauss伪谱方法是一种利用全局插值多项式构建方程的直接配点法,它相对于一般直接配点法的优势在于用较少的节点代入就可以获得较高的精度[3]。
以往利用Gauss伪谱法开展的高速飞行器轨迹数值优化的研究中,国防科技大学的雍恩米、唐国金等人在研究高超声速飞行器滑翔式再入的快速轨迹优化问题中,使用驻点热流密度积分,得到再入过程的热载作为优化目标[4]。但这与本文研究内壁面升温最小的问题仍然不同,为了说明问题,做计算实例如下。
保持初始条件一致,分别通过积分计算内壁面温度的上升,保证二者总热流关相同,得到结果如图1所示。由图1可以看出,在相同的总热载下,不同的加热时间,内壁面温度的上升差异很大,因此,总热载并不能有效地反映飞行器结构的温度变化。

图1 相同总热载下温度上升对比
结合传热学和轨迹数值优化,通过二阶有限差分的方法,将飞行器壳体上的温度按照物面法向进行离散之后,构建有关于各层温度关于时间的状态方程。并将此方程代入动力学微分方程,即将温度作为状态变量考虑,以此开展Guass伪谱法进行飞行轨迹数值优化,并且以末点乘员舱壁温度最低为优化设计目标。
1 优化问题的数学模型
1.1 飞行器动力学模型
忽略地球自转的影响,临近空间飞行器无动力再入段的动力学方程如下
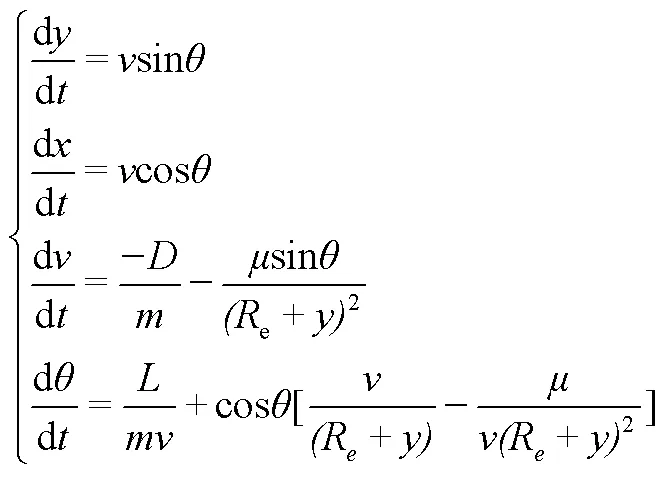
1.2 传热层的模型
1.2.1 传热方程
为了研究本文的问题,需要建立合适的传热分析模型。已有的分析结果表明,如果不需要准确分析连接件附近区域温度分布,可以不必要建立三维模型。因此采用一维简化热分析模型完全能够满足本文优化的精度要求。
由于使用有限插分方法的限制,要求各层的厚度相同。建立一维热分析模型如图2所示,由一系列连续的厚度相同、性能参数不同、对传热起不同作用的材料相互串连而成,最后一层是内部冷结构,各层内部及各层不同材料之间存在沿厚度方向的连续导热。在直角坐标系中的无热源一维瞬态导热控制方程为[6]

式中 ,,及分别为各层所使用材料的密度、热传导系数、比热容、及温度。
1.2.2 传热微分方程
a)中间层的微分方程。
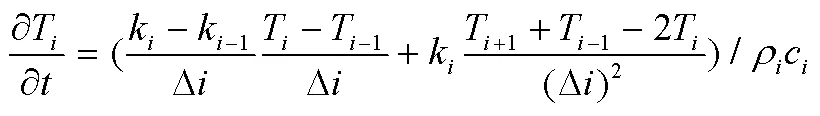
b)外边界微分方程。
1)外边界边界条件。
对于外边界,本文采用第3类边界条件,热平衡方程为[7]

外壁面的能量平衡方程为

气动加热产生的热流如下:

至此,外壁面离散控制方程可以写为

2)边界热流分析。
外边界热流为由气动热产生的冷壁热流,取飞行器迎风面某特征位置为参考点,其计算公式为

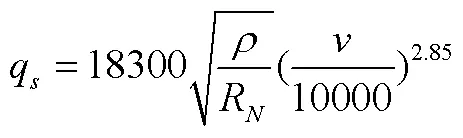
c)内边界微分方程。
对于内边界,一阶离散导热控制方程为

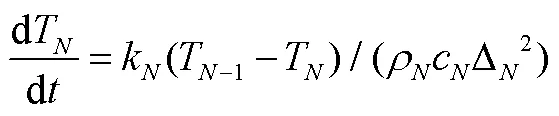
综上,微分方程组如下式所示:

2 利用伪谱法转化问题
2.1 Gauss伪谱法简介
Gauss伪谱方法通过将状态变量和控制变量在一系列Legendre-Gauss(LG)点上进行离散,并将这些离散点作为节点,构造Lagrange插值多项式,来逼近原状态变量和控制变量[8]。再通过对插值多项式求导获得微分矩阵,以矩阵来逼近状态变量对时间的导数,这样就将微分方程约束转换为代数方程约束。性能指标中的积分项和终端状态约束都由Gauss积分计算即可获得性能指标中的积分项和终端状态约束。经上述变换,可将最优控制问题转化为通过代数约束的一系列参数优化求解问题,称为非线性规划问题(NLP),之后利用SQP算法求解该问题[9]。
2.2 连续优化问题的转化
a)时域变化。
使用legendre插值多项式需要保证自变量范围为[-1,1],因此做时域变换:

通过上式,时间区间从[0,f]转换到[-1,1]。
b)将时间离散化。
将变换后的时域离散,获得个LG点。LG点的定义为勒让德多项式的根。
c)状态与控制变量的全局插值多项式近似。

式中 Lagrange插值基函数由下式计算:
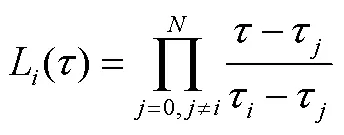
同理,获得控制变量的近似表达式:
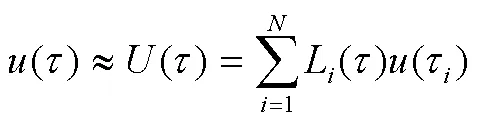
d)微分方程约束转化。
由式(14),即有:

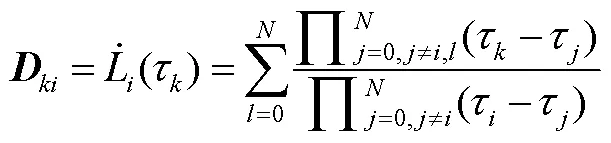
从而将问题由一开始的微分方程约束转变为如下式所示的代数方程约束:

式中=1,…,;= 0,…,。
e)终端状态约束。
上式的状态变量未包含终端时刻节点处的值,终端状态由微分方程对时间积分再加上初始状态值得到,其中,用离散的Guass积分近似原有连续函数积分过程,可得:

f)性能函数指标的近似。
原始含有积分方程的性能函数泛函为
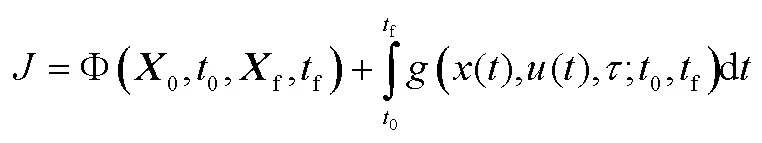
将其中的积分利用Gauss积分方程代换,得到性能指标的新的函数表达式

3 求解优化问题策略
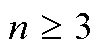
针对上述问题及其特殊性,本文基于Gauss伪谱法提出以下求解大量约束条件下最优飞行轨迹的策略:
a)先利用龙格-库塔法求取式(16),建立合适的控制策略,并利用粒子群算法以防隔热层厚度为优化变量,进行优化以期获得全程再入飞行过程中各控制层合适的温度变化,要求温度变化在材料热受能力之内,且具有一定程度的温度变化,便于优化问题的求解。将获得的结果以LG点转化后的时刻离散,作为Gauss伪谱法优化的初值。
b)利用Gauss伪谱法计算LG点个数=5时刻的结果,获得其节点处离散点的数值之后,利用拉格朗日插值法进行全过程的设计变量随时间的变化曲线的拟合,求解=10的勒让德多项式的解,获得=10时的LG点,通过式(21)将其还原成飞行过程的时刻,利用对=5时刻的节点数值进行一维插值获得这些新的节点处设机变量的值,再利用这些值进行拉格朗日插值法获得最终结果曲线。
c)将获得的结果与代入控制策略的龙格-库塔法的结果进行对比,观察二者的差异。
4 数值计算实例
以远程高速滑翔式再入飞行器为仿真对象,气动参数采用波音公司设计研究的锥形体再入机动飞行器CAV-H的气动数据,并通过拟合获得。飞行器最大升阻比约为2.4,选取气动参考面积为0.35 m2,质量为907 kg,最大飞行攻角和最大升阻比攻角为30°,最大升阻比攻角为10°。再入飞行器初始数值计算初值条件、终端条件及过程相关约束见表1。
表1 数值计算初值条件、终端条件及过程约束
Tab.1 Numerical Calculation of Initial Conditions,Terminal Conditions and Process Constraints
初始条件x/kmy/kmv/(m‧s-1)θ/(°) 0805000-2 T0~T2/KT3/K—— 280280—— 终端条件x/kmy/kmv/(m‧s-1)T3max/K 240020≧500350 过程约束Q/Pa/(°)/(°)— ≧500030—

图3 再入轨迹优化结果

续图3
5 结束语
基于Gauss伪谱法求解高速飞行器再入时的传热问题。创新性地将温度利用有限差分方法作为一个新的状态变量代入伪谱法微分方程组,并整理出各离散点温度与控制变量的关系,与速度、高度等状态变量共同优化,获得结果。优化计算结果表明,弹道轨迹变化切实引起了飞行器壳体温度变化;伪谱法获得结果与龙格库塔法求解的结果基本一致,表明本文使用的方法可靠性较高。本文研究的成果可进一步应用到飞行器的防热问题中。
[1] 闫晓东, 唐硕. 基于伪谱法的亚轨道飞行器返回轨迹优化设计[J]. 西北工业大学学报, 2010, 28(5): 748-751.
Yan Xiaodong, Tang Shuo. Optimal design of return trajectory of suborbital vehicle based on pseudospectral method[J]. Journal of Northwestern Polytechniacal University, 2010, 28(5): 748-751.
[2] 宗群, 田栢苓, 窦立谦. 基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J]. 宇航学报, 2010, 31(7): 1775-1781.
Zong Qun, Tian Bailing, Dou Liqian. Trajectory optimization of near space vehicle ascent stage based on gauss pseudospectral method[J]. Journal of Astronautics, 2010, 31(7): 1775-1781.
[3] 周文雅, 杨涤, 梁新刚. 利用高斯伪谱法求解最优气动辅助轨道转移[J].吉林大学学报(工学版), 2010, 40(5): 454-1459.
Zhou Wenya, Yang Di, Liang Xingang. Use Gauss pseudospectral method to solve the optimal aerodynamic assisted orbit transfer[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(5): 1454-1459.
[4] 雍恩米, 唐国金, 陈磊. 基于Gauss伪谱法的高超声速飞行器再入轨迹快速优化[J]. 宇航学报, 2008, 29(6): 1766-1772.
Yong Enmi, Tang Guojin, Chen Lei. Rapid optimization of reentry trajectory of hypersonic vehicle based on Gauss pseudospectral method[J] Journal of Astronautics, 2008, 29(6): 1766-1772.
[5] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397- 406.
Yong Enmi, Chen Lei, Tang Guojin. A review of numerical methods for aircraft trajectory optimization[J]. Journal of Astronautics, 2008, 29(2): 397- 406.
[6] John D, et al. Hypersnoic and high temperature gas dynamics[M]. NewYork: McGraw-Hill Book Company. American Institute of Aeronautics and Astronautics, 2002.
[7] 薛鹏飞, 龚春林, 谷良贤. 基于轴对称比拟的气动热计算方法研究[J].计算机仿真, 2012, 29(6): 97-100.
Xue Pengfei, Gong Chunlin, Gu Liangxian. Aerodynamic thermal calculation method based on Axisymmetric comparison[J]. Computer Simulation, 2012, 29(6): 97-100.
[8] Huntington G T. Advancement and analysis of a gauss pseudospectraltranscription for optimal control problems[D]. MA: Massachusetts Institute of Technology, 2007.
[9] David Benson. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J]. Journal Of Guidance, Control, and Dynamics, 2006, 29(6): 1435-1440.
Influence Analysis of Heat Transfer Effect on Reentry Trajectory Optimization of Adjacent Space Vehicles based on Gauss Pseudospectral Method
Shao Jia-jian, Xue Peng-fei
(Science and Technology on Space Physics Laboratory, Beijing, 100076)
Based on Gauss Pseudospectral and the second order finite difference method, to study the heat transfer problem in the process of hypersonic flight vehicle reentry, and according to the purpose of the lowest temperature rise in the innermost layer to perform numerical optimization of flight path. The main train of thought. constructing the heat transfer analysis model andthe heat transfer differential equation of each temperature layer according to the heat transfer equation. Substituting differential equation of every temperature layer and dynamic differential equation into the constraint conditions of the differential equation in the pseudo-spectral method, for the trajectory numerical optimization design; constructing lagrangian polynomials with a small number of LG points, and a large number of LG points are obtained through one-dimensional interpolation, to obtain the fitting result curve with higher accuracy. This method is used for numerical calculation of a hypersonic vehicle, and the results verify the feasibility of it.
gauss pseudo-spectral method; heat transfer analysis model; trajectory optimization design
2097-1974(2023)01-0011-05
10.7654/j.issn.2097-1974.20230103
V412.4+4
A
2018-12-14;
2022-12-01
邵嘉健(1994-),男,工程师,主要研究方向为飞行力学。
薛鹏飞(1987-),男,博士,高级工程师,主要研究方向为飞行力学。

