低温跨声速风洞设计中的真实气体效应研究*

黄知龙，王 宁，史志伟，廖达雄

(1. 南京航空航天大学 航空学院， 江苏 南京 210016；2． 中国空气动力研究与发展中心 设备设计与测试技术研究所， 四川 绵阳 621000)

雷诺数的变化主要影响边界层发展和转捩、边界层分离、旋涡流动、激波/边界层干扰、激波/旋涡干扰、底部流动与尾迹、黏性横流等黏性起支配作用的流动[1-4]。由于雷诺数效应的非线性和复杂性，理论和计算流体动力学方法都难以有效预测[5-7]。Kilgore等学者认为低温风洞是设计先进飞行器、应对激烈市场竞争的重要工具[8-9]。降低试验介质的气流温度目前被认为是提高风洞试验雷诺数最有效的技术途径[10-12]。当气体温度降低时，气流密度增大，黏性系数降低。试验气流温度从50 ℃降低到-173 ℃时，模型试验雷诺数提高5倍[13-15]，且速压可保持不变。

低温风洞要求作为运行介质气体的温度在110～320 K范围，气体处于该低温段范围时会出现真实气体效应，其状态不满足完全气体假设。与完全气体相比，低温真实气体效应对风洞洞体回路气动特性的影响是低温风洞气动设计中所不可回避的问题。

描述低温真实气体最精确的状态方程是以级数形式表达的维里方程，但维里方程过于复杂。三次方程中的ARK方程应用广泛[16-17]。Jacobsen等研究了氮气从液化温度到2 000 K、压力到1 000 MPa下的热力学特性[18]。上海交通大学李军进行了低温下真实与完全气体状态方程的热物性比较[19]。中国科学院理化技术研究所柯长磊等针对低温透平膨胀机数值模拟指出完全气体物性库与实际气体物性库的流动结果存在一定偏差[20]。曹学文等针对天然气领域高速膨胀液化装置设计中的真实气体效应开展了研究分析[21-24]。中国空气动力研究与发展中心的江雄等开展了低温增压真实气体效应对运输机气动特性影响数值模拟研究[25]。然而，国内外鲜有报道在低温风洞设计领域的真实气体影响。

本文针对0.3 m低温跨声速风洞的运行温度和压力范围，开展了低温真实气体下的风洞流动参数计算分析研究，以此为基础获得了低温风洞运行温度、总压、马赫数、雷诺数等组合性能包络线。获得的研究结果为该低温风洞总体方案设计和性能评估奠定了技术基础。同时，文中开展的相关分析和得到的初步结论与风洞的具体尺寸无关，因此同样适用于其他尺寸低温风洞的性能计算分析。

1 研究设备简介

0.3 m低温风洞是中国空气动力研究与发展中心自主设计建设的国内首座低温跨声速风洞，已于2015年7月建成。该低温风洞通过向洞体内喷入液氮汽化吸热实现低温运行，以两级低温轴流压缩机为动力驱动洞体回路内气体运行。试验段横截面尺寸为0.325 m(宽)×0.275 m(高)，马赫数范围0.15～1.30，运行总温范围110～323 K，运行总压范围115～450 kPa，单位长度雷诺数模拟试验能力2.33×108/m。该风洞实现的马赫数控制精度优于0.005，总压控制精度优于0.1%，温度控制精度优于0.1 K，总体性能达到国军标先进指标(GJB 1179A—2012)。

2 压缩性因子和比热比

2.1 压缩性因子

对于非完全气体，压缩性因子Z反映了热力非完全特性，是气体温度和压力的函数，多项式计算表达式为：

(1)

式中：P为压力，单位Pa；T为温度，单位K；ρ为密度，单位kg/m3；R为氮气常数，单位J/(kg·K)；中间变量B和C通过式(2)计算。

(2)

其中，bi和ci取值如下：b0=1.370，b1=-8.773×10-2，b2=4.703×10-4，b3=-1.386×10-6，b4=1.462×10-9；c0=5.521，c1=-1.986×10-1，c2=7.817×10-4，c3=-1.258×10-6，c4=5.333×10-10。

2.2 比热比

对于非完全气体，比热比γ反映了气体热量非完全特性，与气体的温度和压力相关，计算表达式为：

(3)

式中：CP为等压比热；CV为等容比热；P为压力，单位Pa；B和C通过式(4)计算。

(4)

其中，mi和ni取值如下：m0=1.867 99，m1=-9.521 87×10-2，m2=5.146 38×10-4，m3=-1.359 50×10-6，m4=1.316 76×10-9；n0=-1.251 26，n1=-4.969×10-2。

纯氮气的压缩性因子Z随温度和压力变化曲线如图1所示。可以看出，随着气体温度的降低和压力增大，压缩性因子Z逐渐减小，偏离完全气体标准值Z=1.0，且温度越低和压力越高时偏差越大。从常温常压下的Z=1.0降至低温增压(100 K、0.45 MPa)时的Z=0.90，偏离完全气体值达到约10%。

图1 压缩性因子与温度和压力的关系(纯氮气)Fig.1 Variation of compressible factor with temperature at different pressures (pure nitrogen gas)

纯氮气比热比γ随温度和压力的变化曲线见图2。可以看出，随着气体温度的降低和压力增加，比热比γ逐渐增大，偏离完全气体标准值γ=1.4，且同样是温度越低、压力越高时偏差越大。从常温常压下的γ=1.40增大到低温增压(100 K、0.45 MPa)时的γ=1.587 5，偏离完全气体值达到约13%。

图2 比热比与温度和压力的关系(纯氮气)Fig.2 Variation of ratio of specific heat with temperature at different pressures (pure nitrogen gas)

3 等熵膨胀关系

基于完全气体状态方程和能量方程可推导出常用等熵流动总静态参数比方程式如下：

(5)

(6)

(7)

若不考虑气体的热力不完全，仅引入气体热值不完全影响，将真实气体的比热比γ代入上述总静态比方程组，可得到试验段气流总静态比值与温度的关系曲线如图3所示，图中试验段马赫数为1.0。可以看出，随着介质温度的降低，常用状态参数(密度、压力和温度)的总静态比值相对于常温出现明显偏离，密度比增大，温度比和压力比则减小；温度越低，偏离趋势越显著。气流总温110 K时，总静温比值的偏差达到约4%，这会影响风洞模型试验测试结果的可靠性。

图3 仅考虑热值不完全时气流参数随温度变化曲线Fig.3 Variation of flow parameters with temperature only considering incomplete calorific value

对于完全气体，等熵膨胀的压力与密度关系满足方程式：

P=ργ

(8)

其中指数为比热比γ，沿等熵线为常数保持不变。而从图2中可以看出，双原子氮气在低温下表现了气体热值不完全性，比热比γ随压力和温度发生变化(不再为常数)，则上述压力和密度的指数方程式(8)也不再成立，以此为基础推导出的方程式(5)～(7)也不再适用。因此，基于完全气体方程得到的低温氮气等熵流动结果则产生了较大的偏差。

研究发现引入一个新的变量(定义为等熵膨胀系数α)代替比热比γ，完全气体方程式(8)在低温真实气体条件下仍成立，则方程式(5)～(7)的形式仍适用，见式(9)，这大大简化了风洞内气流流动参数的分析难度。

(9)

等熵膨胀系数α是比热比γ和压缩性因子Z的组合函数。等熵膨胀系数α由物理方法获取的真实气体等熵流动的压力和密度解代入式(10)确定。

(10)

图4给出了在气流总温为110 K时，不同压力和马赫数下的等熵膨胀系数α计算结果。可以看出，在相同气体温度下，等熵膨胀系数α的值随着压力的增大和马赫数的增大而略有减小。在0.3 m低温风洞的运行温度、压力和马赫数包线内，等熵膨胀系数α值介于1.38至1.41之间。

图4 等熵膨胀系数变化曲线(T0=110 K)Fig.4 Variation of isentropic parameters(T0=110 K)

将风洞在最恶劣工况时(总压0.5 MPa、总温110 K)的低温氮气等熵膨胀系数(α≈1.385 3)代入方程式(9)，得到基于等熵膨胀系数结果与真实气体解的对比曲线如图5所示。可以看出，密度和压力比值基本重合，温度比值略有偏差。两者偏差如图6所示，最大偏差也小于1%，完全可满足工程设计。

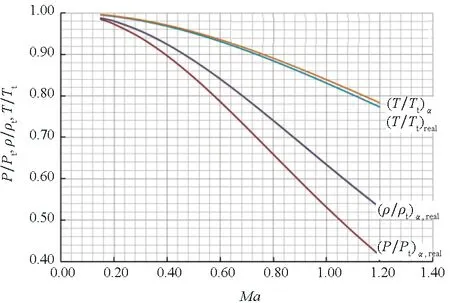
图5 等熵膨胀系数计算解与真实气体解对比曲线Fig.5 Comparison between the results calculated by isentropic parameters and by real gas model

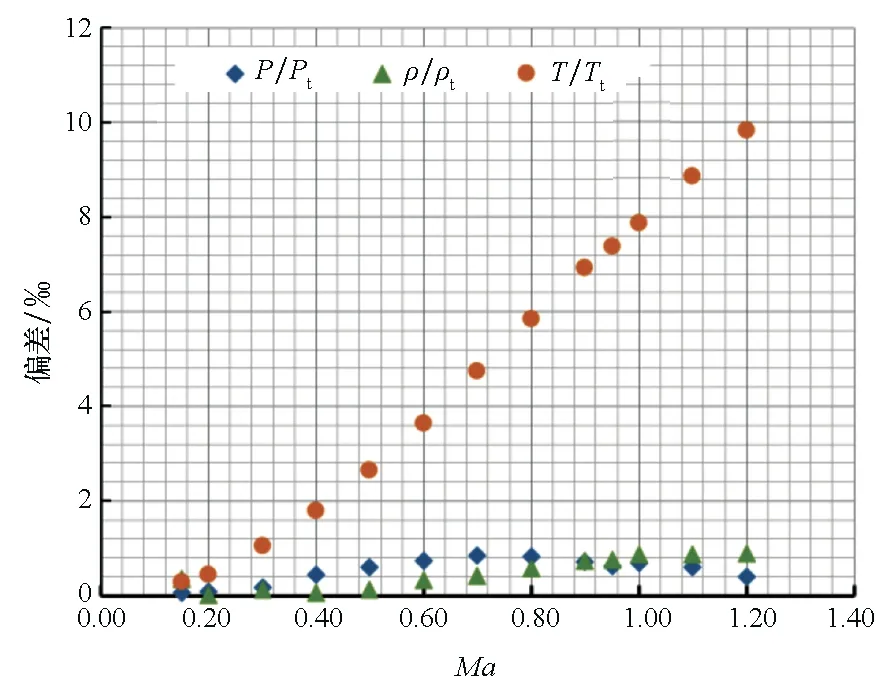
图6 等熵膨胀系数计算解与真实气体解的偏差Fig.6 Deviations between the results calculated by isentropic parameters and by real gas model

4 试验气体液化边界

0.3 m低温风洞可运行的最低总温由多种因素共同决定。试验气体最有可能在模型局部的低压区首先出现冷凝，因此必须确保在最恶劣的工况条件下模型表面气体不出现液化。假设试验气体为完全气体，其从稳定段经喷管段等熵膨胀至试验段，模型当地静压和风洞稳定段滞止压力的比值就唯一决定了模型区马赫数。

在大气环境中约78%体积为氮气，21%体积为氧气，二者均为双原子分子，且两者的分子量基本相等。因此，纯氮气与空气的气体物性基本相同。飞行器在环境温度和氮气介质的风洞中开展试验获得的任何测试结果必然与大气环境中的测试结果相同，因此下文计算讨论了风洞以低温氮气或空气为运行介质时的液化边界。

4.1 纯氮气介质试验

氮气的饱和蒸气压和饱和温度的经验关系表达式如式(11)所示，该经验公式可覆盖三相点到临界点之间的温度范围。

ln(P/101 325)=N1/T+N2+N3·T+N4·

(TC-T)1.95+N5·T3+N6·T4+

N7·T5+N8·T6+N9·ln(T)

(11)

式中：TC为临界点温度，取值126.20 K；T为饱和温度，单位K；P为饱和压力，单位Pa；Ni取值如下：

以此得到液氮在三相点至临界点范围下的饱和温度与蒸气压关系曲线见图7。可以看出，常压(1.013 25×105Pa)下氮的饱和温度为77.347 K(B点)；三相点温度为63.748 K(A点)，对应的压力为0.125 34×105Pa；气态临界温度为126.200 K(C点)，对应压力33.994 54×105Pa。风洞模型的最低运行气流温度决定于该饱和温度与蒸气压的关系曲线。

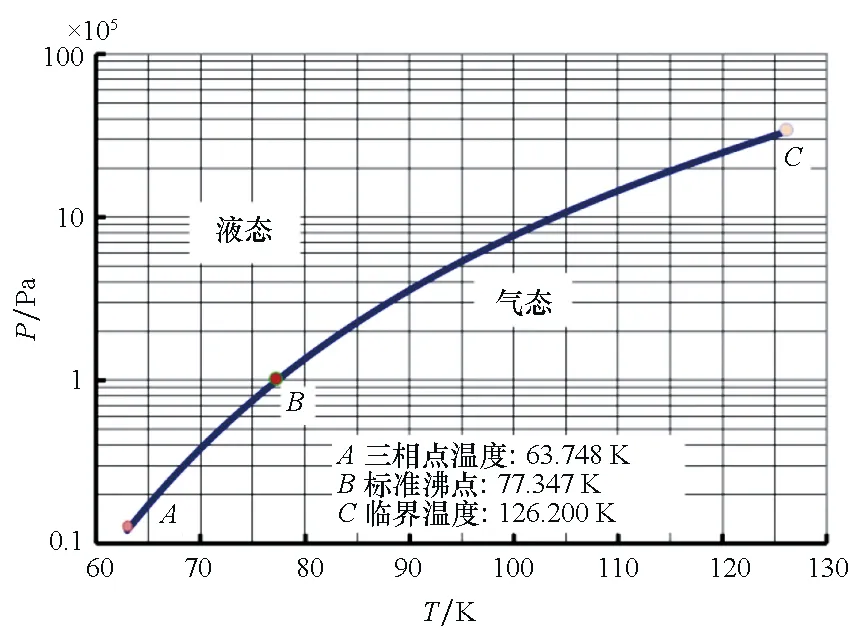
图7 氮气饱和温度与蒸气压关系曲线Fig.7 Relationship between saturation temperature and vapor pressure for nitrogen gas

风洞带模型试验时，由于模型区堵塞度变化，存在局部的气流加速区，试验时应避免在局部高马赫数区域出现气体液化现象。图8给出了自由流马赫数Ma∞与模型表面当地最大马赫数MaL,max的典型关系曲线，局部气流马赫数明显高于自由流。

图8 试验段自由流马赫数与模型当地马赫数关系曲线Fig.8 Comparison between free stream Mach number and local Mach number for model

基于氮气饱和蒸气压关系曲线和模型当地最大马赫数曲线，风洞在不同马赫数和运行总压下的最低允许运行总温可通过方程式组合(9)～(11)计算得到。图9给出了0.3 m低温风洞试验段不同最大马赫数和总压组合所对应的气体总温饱和边界。最大马赫数MaL,max范围从0.20至1.80，最大总压500 kPa。由图可以看出，风洞允许的最低运行总温Tt,min与试验段最大马赫数MaL,max和风洞运行总压Pt均成正比。限制风洞运行参数在此包络线内就可保证不出现试验气体的液化现象。

图9 风洞最低运行总温与当地最大马赫数和滞止压力关系(纯氮气)Fig.9 Relationship between lowest total temperature, local Mach number and stagnation pressure of the wind tunnel (pure nitrogen gas)

风洞试验段自由流马赫数Ma∞=1.0模型试验时，气体温度饱和边界与试验雷诺数的关系曲线如图10所示。图中设定了5种不同的运行总压Pt和模型附近3种最大当地马赫数MaL，max。可以看出，对于给定的运行总压，所能获得的试验雷诺数随着当地马赫数MaL，max的增加而降低，气体的饱和边界和液化决定于当地的运行温度和压力，而不是试验段入口的自由流参数。图中当地马赫数涵盖了该风洞自由流为声速时模型表面的最大可能马赫数。因此，基于试验中模型当地最大马赫数预测值和实测结果，可确定风洞运行温度和压力的组合，以避免因试验气体液化而影响到测试数据的质量。

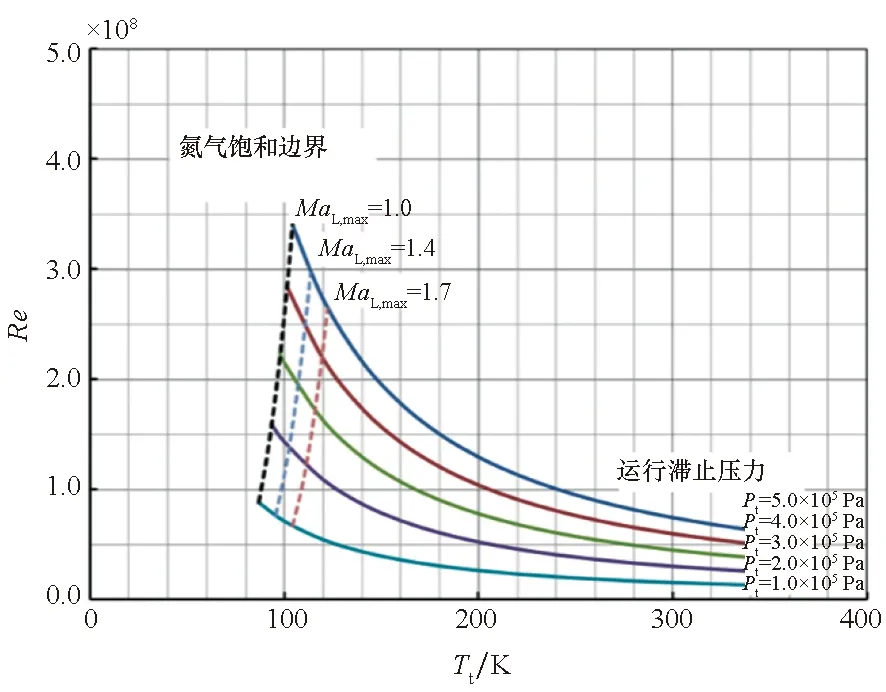
图10 考虑气体冷凝下的风洞运行雷诺数包络线Fig.10 The Reynolds number envelopes of the wind tunnel for considering gas condensation

4.2 标准空气介质试验

对于标准混合空气介质，在三相点至临界点范围下的饱和温度与蒸气压关系曲线如图11所示。可以得到，空气的三相点温度为59.75 K，压力0.024 32×105Pa；气态临界温度132.63 K，压力37.834 76×105Pa。

图11 空气饱和温度与蒸气压关系曲线Fig.11 Relationship between saturation temperature and vapor pressure for atmosphere

与纯氮气介质相同的计算思路，利用空气饱和蒸气(露点)温度数据(参考NIST)可以计算得出空气介质允许的风洞最低运行气流总温，以避免出现气体冷凝，如图12所示。

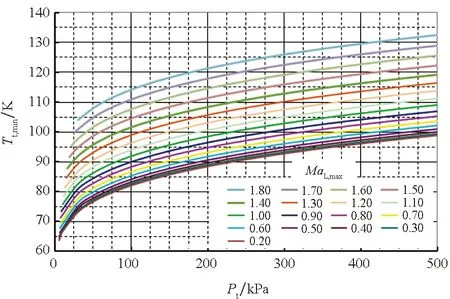
图12 风洞最低运行总温与当地最大马赫数和滞止压力关系(标准空气)Fig.12 Relationship between lowest total temperature, local Mach number and stagnation pressure of the wind tunnel(standard atmosphere)

计算结果覆盖最大当地马赫数达到1.80，最大总压500 kPa。对比纯氮气介质的计算结果可以明显看出，在相同的压力和马赫数下，氮气介质时的运行总温可以更低。比如，在运行总压200 kPa、当地最大马赫数Ma=0.90时，氮气介质的最低允许运行总温为93.65 K，而空气介质则为98.85 K。因此，在相同试验模型下采用氮气介质可以获得更高的模型试验雷诺数能力，雷诺数增加约8.7%。

4.3 空气-氮气混合气体试验

很多情况下，也可通过干燥空气直接掺混液氮进行低温试验，此时试验介质就是空气和氮气的非标准混合气体。为了简化计算分析，假设混合气体就是氮气和氧气，则气体的液化点可通过方程式(12)计算。

(12)

式中：P为空气总压，单位Pa；PO为氧的蒸气压，单位Pa；PN为氮的蒸气压，单位Pa；FO为氧在混合气体中的摩尔分数。

混合气体中氧气的摩尔分数FO从0(纯净氮气)到0.21(空气)的气体饱和温度与蒸气压关系对比曲线如图13所示。一旦确定了不同温度下的饱和蒸气压，利用式(11)和式(12)就可建立最低运行总温与马赫数和压力的关系式。前文中的图12和图9就是风洞运行介质分别为标准空气和纯氮气两种极限工况下的最低运行温度包络线。

图13 不同组分气体的饱和温度与蒸气压关系曲线Fig.13 Relationship between saturation temperature and vapor pressure in different gases

5 结论

本文系统分析了低温跨声速风洞的真实气体效应，即热力和热量不完全带来的影响，建立了低温风洞流动参数计算模型。主要结论包括：

1)将等熵膨胀系数α引入完全气体流动方程可获得满意流动参数计算结果，与真实值的最大偏差小于1%。

2)计算确定了低温真实气体条件风洞试验段为不同介质时的气体液化边界。

3)低温运行时只考虑试验气体热值不完全时会得到错误流动状态结果，真实气体效应的影响应同时考虑热值和热力的不完全。