混合载波系统高阶计算分集方法

冯雨晴, 房宵杰, 沙学军, 宋 鸽

(1. 哈尔滨工业大学电子与信息工程学院, 黑龙江 哈尔滨 150001;2. 中国电子科技集团公司第五十四所通信网信息传输与分发技术国家重点实验室, 河北 石家庄 050080)

0 引 言

在通信技术迅猛发展的洪流中,分集技术、复用技术都在历代移动通信系统中扮演着重要角色,在探索分集增益的过程中,如何合理地利用时间、频域与空间资源是研究重点。文献[1-2]的研究结果表明,多天线系统分集技术在提供分集增益的同时,也能提供复用增益,它充分利用了时间资源和空间资源,将时间分集与空间分集相结合,同时获得了时间和空间上的自由度。复用增益与分集增益分别代表了通信系统的有效性与可靠性,文献[3]提出的空时分组码可以同时实现满分集增益与满复用增益,使矛盾的双方得以短暂地统一。随后,文献[4]研究了更具一般性的空时码——正交空时分组码。

与Alamouti[3]兼顾分集与复用不同的思路,是根据实际情况在二者之间加以权衡。文献[5]提出根据实际信道条件在分集与复用中二者择其一的方案,它是一种选择算法,并不能满足系统的需求,于是出现了一些针对特定系统的折中方案。文献[6-8]则论述了一种最优折中方案,为多入多出系统的分集与复用结合提供了一种思路。随后不久,文献[9-11]针对协作分集系统做出了分析,分别研究了采用不同中继转发模式的系统的折中曲线,但此折中方案仍然损失了一部分复用增益,以换取分集性能。文献[12-13]提出了基于广义混合载波的计算分集(computation diversity, CD)方法,在不占用多余时频资源的前提下,通过数据块分割构造获取额外分集增益,同时复用增益基本不受影响。

而在双弥散信道下,基于加权分数傅里叶变换(weighted fractional Fourier transform, WFRFT)的混合载波(hybrid carrier, HC)系统信号中含有多个时域信号分量与多个频域信号分量,它同时具备单载波(single carrier, SC)调制与多载波(multi carrier, MC)调制的优点,可以降低双弥散信道对通信系统造成的影响[14-15],其能量分布更平均,可以降低干扰,提高系统性能[16]。WFRFT于1995年由Shih提出[17]。2010年,Mei等[18]首次将离散WFRFT引入到数字通信系统,并且揭示了加权系数和加权函数的关系,随后正式提出了基于四加权分数阶傅里叶变换(4-WFRFT)的载波系统,该载波系统也被称为HC[19]。通过改变加权调制阶数、控制WFRFT信号的SC分量和MC分量的比例,证明了HC系统在一定的调制阶数下,相比于传统载波体制,有更好的抗双弥散信道衰落的特性[20]。分数傅里叶变换的阶数选择对HC系统的性能有着至关重要的影响。Shuang等[21]分析了时频衰落信道下频率偏移对WFRFT系统的影响,推导了由载波间干扰和符号间干扰引起的信号干扰比,证明了WFRFT系统通过选择最优的分数阶,在存在频偏的基础上,相比SC系统和MC系统均具有优越性。Hui[22]提出了一种双选信道下的4-WFRFT最优阶选择方法,推导了载波干扰比的表达式,然后通过最大载波干扰比得到最优阶数,根据所获得的信道状态信息选择4-WFRFT的最优阶数因子,在SC和MC系统之间进行切换以达到匹配信道的目的。此外,扩展WFRFT的时频分量分布灵活性和能量分布平均性为其与传统载波体制的结合在理论上提供了可能[23-24]。Pan等[25]将载波方案切换和自适应调制编码与功率控制相结合,以最大限度地提高系统吞吐量。基于WFRFT的HC系统在物理层安全传输方面也有着广泛应用,Liang等[26]提出了一种基于WFRFT的变换域通信系统组合系统,利用WFRFT信号能量分布扁平化的特点对通信系统进行了加密,以保证通信的安全性。WFRFT信号包含多个时域分量和频域分量,其信号本身具备成为分集技术的特点[27-28]，而分数域混合载波信号也具备进一步提升分集增益的空间。

本文利用WFRFT信号设计适用于分数域HC系统的CD方法,将信号能量扁平化分布,以继续提高HC系统在双弥散信道下的分集性能。当系统内存在剩余资源可供利用时,其分集增益仍有可提升空间。探索扩展长度增加情况下的高阶CD方法,并在此基础上提出高阶数据块反转策略,将其与高阶CD方法联合应用,以进一步降低系统误码率。

1 计算分集

分集技术一直是抗信道衰落的主流技术之一。某条路径处于深度衰落的概率很大,而当深度衰落发生时,任何通信方法都可能会出现错误。将数据重复传输,并通过各自独立衰落的多条信号路径,可降低某条路径处于深度衰落给整个系统带来的风险,从而提高通信系统的抗衰落能力。以时间分集为例,多个时隙传输同一信号,在获得分集增益的同时,无复用增益。而利用WFRFT可以将原信号变换为多个分量的复合信号,实现类似分集的效果,获得分集增益;与此同时,WFRFT所提供的四分量叠加信号与HC体制相对应,可避免扰乱原有载波体制。

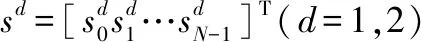
图1 发射信号预处理Fig.1 Transmit signal preprocessing

通过计算变换得到不同的信号分量,各信号分量经历具有一定统计独立性的信道,利用变换域计算得到合并的信号,这样通过计算取得信号分量并通过计算合并分量的过程称为计算分集(computation diversity, CD)方法。经过变换的数据分布区间长度为原来的2倍,从能量角度而言分布更加均匀;从信道角度而言,二者能够经历两条独立衰落的信道,降低共同衰落的概率,从而提高抗衰落性能,以获得额外的分集增益。

图2为第(i+1)比特发生深衰落对CD信号的影响的示意图。在两个信号分量功率相等的情况下,若某比特发生深衰落而全部丢失,其备份第(2N-i)比特信息并未受到影响,致使该比特总功率衰减3 dB,相对于完全衰减,该比特的备份有更大可能地满足接收机灵敏度,从而使误码率性能得到保障。

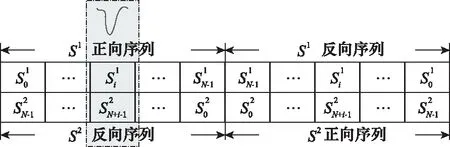
图2 CD方法抗深衰落原理Fig.2 Anti-deep fading principle of CD method

在双弥散信道下,HC系统更具优势,其既有时域分量对抗时间弥散,又有频域分量对抗频率弥散。而这样的信号结构可以通过WFRFT获得,在得到这样一组时域信号的同时,还将获得一组频域对偶信号。

分数域四分量CD(fractional domain four-component-CD, FRFC-CD)算法的原理框图如图3所示。这样变换后的信号将含有f(t),f(-t),F(ω)与F(-ω)4个分量。可将这种利用WFRFT完成的CD称为FRFC-CD算法。

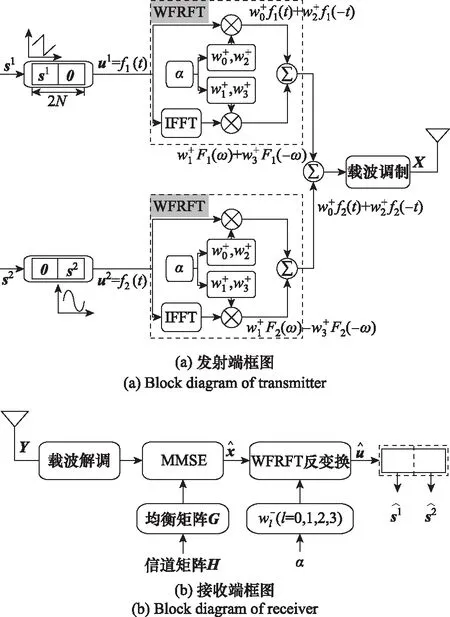
图3 FRFC-CD算法的原理框图Fig.3 Block diagram of FRFC-CD algorithm’s principle

(1)

(2)

频域信号Fi(ω)=F[fi(t)]由时域信号fi(t)经傅里叶变换得到,F为傅里叶算子。再将该待发射信号进行载波调制、功率分配等处理,最后经由天线发射。接收端接收到的信号采用最小均方误差(minimum mean square error, MMSE)均衡处理信号,得到补偿衰落的信号,进行下变频处理去除载波,获得接收端基带数据

Y=HX+Z

(3)

(4)

均衡后根据已知的逆变换参数,对接收到的信号进行α阶逆WFRFT,变换系数与发射端匹配、采用同一参数生成。完美复原信号时,两条数据可以将各自信号从时域信号的对应位置截取出来。

(5)

(6)

(7)

h(·)表示取反函数。对于同时存在多普勒扩展和多径效应的双弥散信道而言,应用WFRFT可以有效地提高其抗时域衰落的能力,而分数域正向信号与反向信号的叠加构成了互相备份,得以进一步加强抗衰落能力。

将原始长度为N的两组数据进行FRFC-CD,MC成分部分在每次运算时共需要2次2N点的快速傅里叶变换(fast Fourier transform, FFT)运算(一次FFT需要进行Nlog22N次乘法和2Nlog22N次加法)和8N次复数乘法计算,SC成分部分只需进行8N次复数乘法计算。因此,可得FRFC-CD方法的总时间复杂度为O(NlgN+4N)。

分别对单/双数据流FRFC-CD、SC和MC的误码率性能进行仿真,归一化多普勒频移FDT=0.01,多径时延扩展为τ=[0,4,8,12]·Ts,取变换阶数α为0.5,结果如图4所示。无论当前信道下FRFC-CD方法的通信负载量如何,其误码率性能均优于SC和MC。低信噪比时,单数据流FRFC-CD有明显性能增益,双数据流则不太明显;FRFC-CD带来的分集优势随信噪比变高逐渐变大;在高信噪比下,FRFC-CD在传输单倍数据时优于传输双倍数据约5 dB。单倍数据流的FRFC-CD频谱效率只有正常通信的一半,以频谱效率换取误码率性能,同时具备应对突发通信任务的能力。在插入第二组数据后,牺牲少量误码率性能换取二倍的频谱效率,此时性能仍优于传统SC和MC系统。

图4 FRFC-CD,SC和MC的比特误码率曲线Fig.4 Bit error rate curve of FRFC-CD, SC and MC

WFRFT系统可以退化为SC系统(离散傅里叶变换扩展的MC系统)或MC系统,其信号内部SC成分和MC成分的比例可以通过变换阶数α进行调节,同时信号的抗频选和抗时选能力也会随之改变。如图5所示,信道条件不变,当α=0.5时,FRFC-CD的性能优于其他两种情况。通过变换阶数的选取可以改变时频分量能量的配比,这使得在已知信道状态信息的条件下,针对不同信道情景下的动态补偿成为可能,即在每个用户总功率受限的情况下,将更多能量向信道条件较好的数据块倾斜;而针对信道条件未知的情景,在相同的衰落概率下,悬殊的功率分配将会给大功率信号衰减带来更大的风险,这种损失显然是致命的。因此,在随机衰落的情况下,等功率分配显然是更好的选择。变换阶数α的选取会影响FRFC-CD的性能,通过优化α也可以起到优化CD方法的作用。对于全知信道,存在使误码率最低的最佳变换阶数。

FRFC-CD引入了WFRFT,在双弥散信道下具有显著优势,适用于HC系统。同时,CD本身同样具备允许多址接入的特点。值得注意的是,经过上述变换后的信号所占频谱宽度、码块持续时间以及空间资源均维持不变,也就是说,CD是在不占用额外物理层资源的前提下获取分集增益的。

图5 不同变换阶数α下的比特误码率对比Fig.5 Comparison of bit error rate under different α

2 高阶CD

FRFC-CD是基于双时隙扩展的CD方法,通过适当的补零操作可以使信号能量分布更加平均,达到抗衰落的目的。当系统中有更多剩余资源可供利用时,数据块长度进一步延长,此时如能将信号扩展至充满整个数据块,那么信号能量将被进一步平均,CD性能得以进一步提升。那么随之而来的问题是,如何扩展、效果怎样以及上限的位置。

由于WFRFT的每次变换都是对称变换,因此FRFC-CD变换后的长度只能是变换前的2L倍。将L称为分集阶数,变换后的数据所占资源称为2L分量,那么第1节提出的CD为一阶计算分集。假设可以无限扩展、多次变换,通过长度可调节的FRFC-CD可使每组待传输数据都充满整个数据块,其能量分布最为平均,抗衰落能力最强。

首先考虑传输固定数据量A,增加扩展长度。如图6所示,对于总功率固定为P的数据A,分别进行2倍补零和4倍补零,然后进行能量平均,与不进行补零扩展的原始信号和4时隙分集进行对比,方块高度代表发射信号功率。在不考虑接收机灵敏度的前提下,随着扩展长度变长,能量平均化的情况越来越好。对于4倍扩展的情况,如果只进行一次FRFC-CD,那么信号能量将集中于第1、第4两个数据块内。因此,设计适用于多时隙扩展的高阶CD集,以变换次数为阶数,其目的是将能量平均分布到整个资源块。

图6 多分量扩展CD方法帧结构及能量分布Fig.6 Frame structure and energy distribution of multi-component extended CD method

在双弥散信道下对图6设计的4种方案的误码率和频谱效率进行仿真,结果如图7与图8所示。假设数据长度为64比特,双弥散信道,归一化多普勒频移为FDT=0.01,最大多径时延为τmax=12Ts。

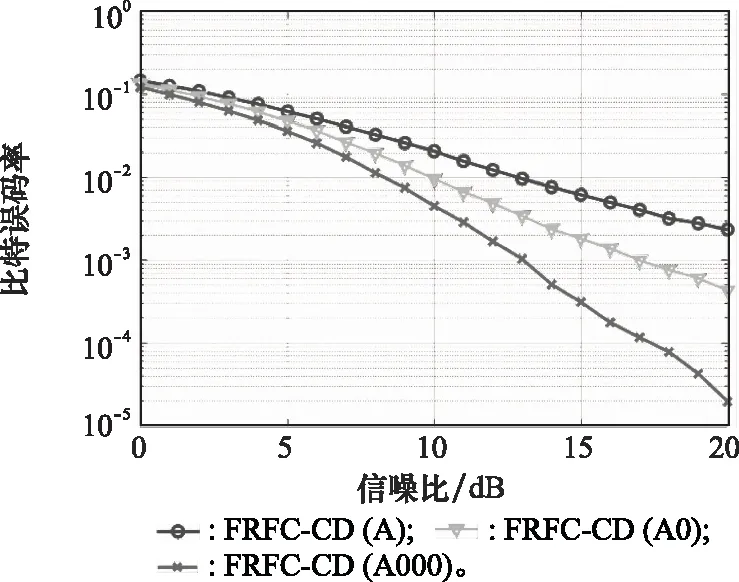
图7 多分量扩展FRFC-CD比特误码率曲线Fig.7 Bit error rate curve of multi-component extended FRFC-CD

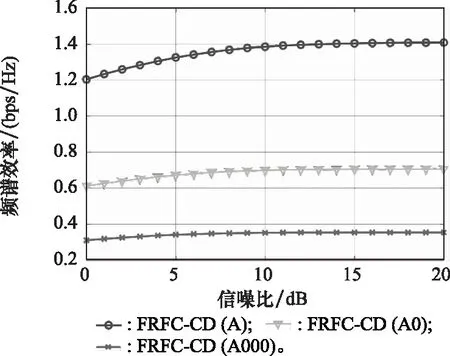
图8 多分量扩展FRFC-CD频谱效率曲线Fig.8 Spectrum efficiency curve of multi-component extended FRFC-CD

仿真结果表明,随着扩展长度增加,误码率性能大幅提高,随之而来的是频谱效率的下降。在数据长度固定的情况下,补零长度越长,误码率性能越好。与长度相等、总功率相等的频率分集误码率性能基本一致。补零后数据长度为原数据长度的n倍,频谱效率为原来的1/n。与长度相等、总功率相等的时间分集频谱效率基本一致。牺牲部分有效性,可换取可靠性传输。

在总功率固定的前提下,补零长度过长会导致发射信号功率过低,不易识别。如果发射信号功率低于接收机灵敏度,信号将不会被接收,那么理论上CD长度扩展应该是有限制的。因此,长度自适应FRFC-CD的扩展阶数上限,应满足每个扩展分量的功率均高于接收机灵敏度,即:

(8)

式中:Pr为总发射功率,Se为接收机灵敏度,单位均为W。根据第三代合作伙伴计划(3rd generation partnership project, 3GPP)的计算方法,得到其理论值为

Se=10lg(KT)+10lg(BW)+NF+SNR

(9)

式中:K为玻尔兹曼常数;T为绝对温度;BW为带宽;NF为噪声系数;SNR为接收机误码解调门限信噪比。

假设取常温T=293.15K,噪声系数为1.2 dB,考虑采用全球移动通信系统(global system for mobile communications,GSM)2.44%误码解调门限,信噪比为9 dB。对于12.5 kHz带宽,根据式(9)接收机灵敏度可计算为Ps=-122.76 dBm。假设发射信号为Pt=30 dBm,接收机距离基站0.1 km,根据自由空间传播模型,信号损耗约为R=101.28 dB,那么,接收信号功率可计算为Pr=Pt-R=-71.28 dBm。此时,根据式(8)粗略计算可得L<16。因此,该场景下最多可以实现16阶计算分集。当数据量固定时,将数据扩展为原始数据的2N倍,可以获得更好的误码率性能,且扩展长度越长、误码率性能越好,其扩展长度上限受系统固有频率资源和接收机灵敏度的双重制约,其性能与同长度、等功率的时间/频率分集相当。

通过延长数据块长度、利用剩余可用频谱资源进行多分量扩展CD,可以有效提高CD算法的误码率性能。但从能量平均化分布抗衰落角度而言,当CD扩展长度进一步加长时,以单个数据块为研究对象,其信号仍然集中于两个数据块内。这样,随着扩展长度增加,每一个数据流所占资源长度与总资源长度的比例进一步减小,这使得其抗深衰落能力减弱。那么,若要每一组数据都能够平均分布在整个资源块上,就需要高阶CD方法。图9所示为基于多分量扩展的L阶FRFC-CD算法流程图。

发送端操作步骤如下:

步骤 1补零。在待传输数据后进行补零操作,补零后数据块总长度应为2LD,待传输数据长度为kD,其中D为原始数据最小分组长度,L为正整数,k为正整数。

步骤 2一级扩展加权变换。将整个数据块分为2L-1个长度为2D的一级数据块,每个一级数据块分别进行-α阶WFRFT。

步骤 3二级扩展加权变换。将整个数据块分为2L-2个长度为22D的二级数据块,每个二级数据块分别进行-α阶WFRFT。

步骤 4以此类推,直到完成L级加权变换,形成待发射信号。

接收端操作步骤如下:

步骤 1均衡。根据均衡算法对接收信号Y进行均衡。

步骤 2加权反变换。将步骤1得到的信号进行α阶WFRFT。

步骤 3r级加权反变换。将步骤2中的信号分为2r个长度为2L-rD的数据块,对每个数据块分别进行α阶WFRFT,直到完成共(L-1)级反变换。

步骤 4获取原始数据估计信号。将步骤3中的信号按时序取前kD比特,得到输出信号。

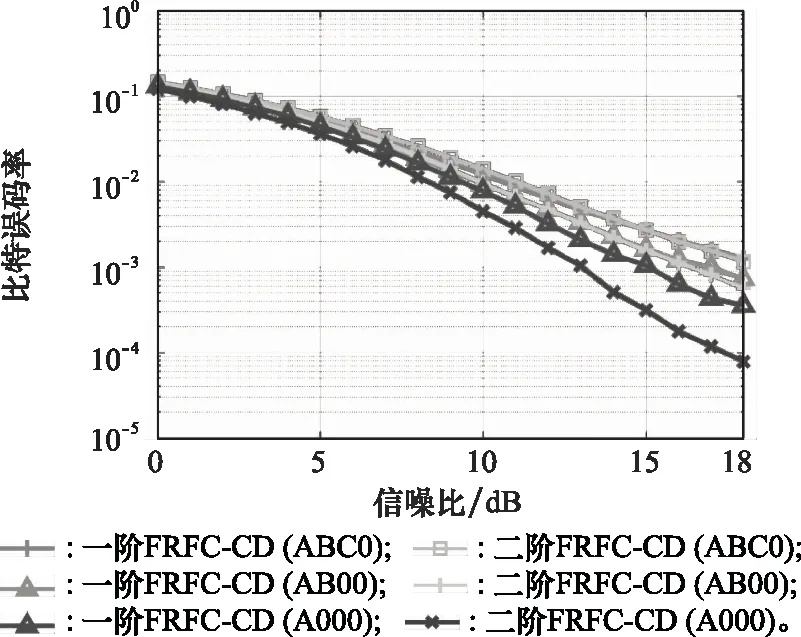
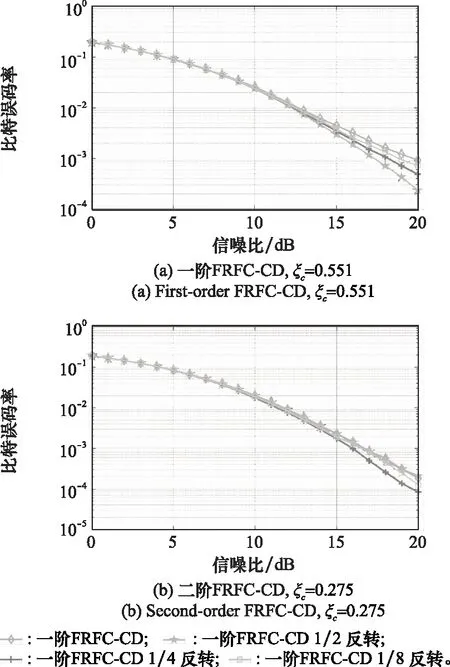
以二阶CD为例,4倍长度的数据分别经过一阶和二阶计算分集后的能量分布图如图10所示。无论原始数据量占据总资源块的比例为多少,在经过二阶CD变换后,每组数据都能均匀地分布在整个资源块上,达到能量分布最为平均的效果。因此,对于总扩展长度为原始数据最小资源块长度2L倍的数据,最多只需要L阶CD,即可完成最优能量分布,其能量分布平均情况优于1～(L-1)阶变换,此时零向量插入位置是无关因素。若采用低阶(

图10 一阶FRFC-CD与二阶FRFC-CD能量分布对比Fig.10 Comparison of energy distribution between first-order FRFC-CD and second-order FRFC-CD

接下来,对上述3种数据量的阶数不同的FRFC-CD误码率进行仿真,如图11所示。仿真结果表明,在总扩展资源长度为原始最小资源块长度4倍的前提下,原始数据占比为2/4、3/4或4/4 3种情况,二阶FRFC-CD的误码率性能较一阶FRFC-CD均有所提高,且原始数据所占比例越小,增益越大。

图11 一阶FRFC-CD与二阶FRFC-CD的比特误码率对比Fig.11 Bit error rate comparison between first-order FRFC-CD and second-order FRFC-CD

接下来,讨论高阶CD在标准瑞利信道下的理论误码率。多进制正交幅度调制(multiple quadrature amplitude modulation, M-QAM)调制在加性高斯白噪声(additive white Gaussian noise, AWGN)信道下,SC系统、MC系统或HC系统的系统误符号率(symbol error ratio, SER)可统一表示为

(10)

(11)

(12)

那么,采用M-QAM调制的N阶计算分集,在标准瑞利信道下的平均误码率表达式为

(13)

3 能量平均化策略

CD中新的传输信号由原始信号分量与反转信号叠加构成,如图12所示,二者相关性由数据块两端向中间逐渐变大。假设CD叠加信号中存在相干时间,如果si与它的反转比特之间的时间间隔小于相干时间,那么二者将不能独立衰落,此时出现共同衰落的概率增大,系统分集增益也会因此受到损失。

高阶CD同样存在数据块接口处相关性过高的问题,其带来的性能下降与相干时间和相同符号间距离的相对大小有关。参考相干时间的定义,根据文献[30],在信号变化非常迅速时,相干时间定义为相关函数大于0.5时所对应的时间:

(14)

式中:fd=Bd/2为最大多普勒频移,Bd为多普勒频谱带宽。在瑞利衰落信号变化十分缓慢的条件下,相关时间为

(15)

这里采用式(9)和式(10)的几何平均值作为相干时间:

(16)

而fd=FDT·fs,代入可得

(17)

定义相干系数为相干时间与符号持续时间和数据块长度的比值:

(18)

其物理意义为处于相干时间内的符号数与数据块总长度的比值。定义相同符号距离ds为数据块相关性较高的区域内相距最远的两个符号间的距离,考虑通常情况0

图12 一阶FRFC-CD发射信号相关性示意图Fig.12 Schematic diagram of the transmit signal correlation of the first-order FRFC-CD

根据上述假设,做出合理猜想:发射信号由时域正向分量f(t)与时域反向分量f(-t)构成,如果将该信号进行适当的反转、变换,使信号的相关性降低,那么同一符号的各个分量发生共同衰落的概率也会随之降低,达到降低误码率的目的。图13为数据块反转方法示意图,图中长度为LB的数据块是由WFRFT的时域分量和时域反转分量叠加而成的。为了确保正确的传输,发射端与接收端的反转图样应保持一致。

首先考虑1/2数据块反转,假设数据块总长度为LB,将时域叠加序列等分为2个部分,并将后半部分码块取反后置于原位置,构成新的信号。这种构造可以将符号距离由原本的1～(LB-1)调整为LB/2,即经过1/2数据块反转后，所有相同符号间的距离均为LB/2,ds/LB=1/2。其次,1/4数据块反转是将原始信号划分为长度相等的4个部分,将偶数块数据取反后置于原位置,得到变换后的信号,ds/LB=1/4。以此类推,1/8数据块反转直至更高阶的数据块反转策略,也要经历等长划分、偶数块反转等操作。

图13 能量平均化策略反转图样Fig.13 Energy averaging strategy reversal pattern

考虑一阶FRFC-CD方法与数据块反转方案匹配。当ξc≤ds/LB=1/2时,1/2数据块反转策略可以将所有相同符号间距离ds都拉长到LB/2,使所有相同比特均处于相干时间外,而进一步地，其他反转则会使个别符号重新回到相干距离内,所以理论上,对于ξc≤0.5的情况,1/2数据块反转策略为最佳反转策略。当ξc趋近于0时,受相干时间影响的比特较少,1/2数据块反转策略虽能使误码率降低,但增益不会非常明显;当ξc趋近于1/2时,是否反转将影响半数数据,此时1/2数据块反转策略带来的增益增加。当ξc>0.5时,信道相关性较高,大部分数据都笼罩在相干时间之下,由1/2数据块反转策略带来的好处随着ξc趋近于1而逐渐降低。

类似地,对于阶数为L的高阶FRFC-CD而言,进行1/(2L)级数据块反转应为最佳反转策略。如二阶FRFC-CD对应的最佳反转策略应为1/4数据块反转,4阶FRFC-CD对应的最佳反转策略应为1/8数据块反转。当ξc趋近于1/(2L)时,数据块反转带来的性能增益增加。图14所示为一阶和二阶计算分集应用数据块反转策略的误码率曲线。

图14 FRFC-CD应用反转策略的比特误码率曲线Fig.14 Bit error rate curve of FRFC-CD with reversal strategy adapted

对于一阶FRFC-CD计算分集而言,1/2数据块反转策略为最佳策略,当ξc趋近于0.5时,效果最好。对于二阶FRFC-CD而言,1/4数据块反转策略为最佳策略,当ξc趋近于0.25时效果最好。虽然信道条件无法改变,但可以通过延长数据块长度LB的方式使得ξc趋近于目标位置。因此,将ξc代入式(11)可得,L阶FRFC-CD最佳匹配反转策略为1/(2L)数据块翻转策略,对应最佳设计数据块总长度为

(19)

结合高阶FRFC-CD数据块长度,LB,L取最接近的2的整数次幂即可。

FRFC-CD信号中部相关性较高,这是由其数据结构决定的。通过不同的反转图样可以有针对性地获取额外分集增益,进一步优化计算分集误码率性能。反转图样的选择与计算分集阶数有关,受信道相关性影响而表现不同,可通过调节数据块长度达到理想性能。

4 结 论

本文针对多分量扩展CD的能量分布不均匀问题提出了高阶CD方法,针对高阶CD数据块内部部分点位相关性过高的问题,提出了基于数据块反转的能量平均化策略,并进行了相应的仿真模拟,主要结论如下:

(1) 本文提出的FRFC-CD在双弥散信道下可提供很好的分集效果,提出的高阶CD方法能够优化多分量扩展CD的能量分布情况,提高误码率性能和分集增益。

(2) 计算分集阶数受剩余可用物理层资源和接收机灵敏度的共同限制,可用物理层资源越多、接收机灵敏度越高、路径衰减越小,可用分集阶数越高,可用资源总长为LB时,最佳变换阶数为log2LB,仿真结果与预测结果吻合良好。取最佳变换阶数时,零向量插入位置为无关因素,在变换阶数的取值低于最佳变换阶数时,零向量的插入位置会对最终结果产生影响。

(3) 能量平均化策略可以进一步提升计算分集的性能,L阶计算分集应当匹配1/(2L)级反转图样,总扩展长度为2LTc/TS时效果最好。

CD不占用额外物理层资源、不破坏原本载波体制、不改变信号本来优势,在未来多种载波混合场景下均有较好的应用前景。其既可作为单独的分集方法应用,亦可作为预编码方案应用于SC和MC系统。