三元组近场效应的馈电系数修正与各向异性分析

唐 波, 鲁嘉淇, 郭琨毅, 金从军, 盛新庆

(1. 北京科技大学计算机与通信工程学院, 北京 100083; 2. 北京理工大学集成电路与电子学院射频技术与软件研究所, 北京 100081; 3. 北京仿真中心, 北京 100037)

0 引 言

半实物射频仿真是一种实物在回路仿真,其将待测试的雷达导引头实物引入仿真回路,以在最大程度上模拟真实试验环境,从而得到最逼近真实情况的结果。同时,半实物仿真仅需在微波暗室中进行,克服了外场试验费用较昂贵的不足。因此,半实物射频仿真已成为雷达导引头研发过程中的一个重要环节。在世界上的一些主要国家和地区,都建立有半实物射频仿真实验室,比较著名的有美国的陆军高级仿真中心、埃格林空军基地导弹仿真实验室,俄罗斯“雷达MMS”科工公司,英国的马可尼公司等[1-2]。我国也在相关的科研院所建立了半实物射频仿真实验室,例如上海航天局等[3]。这些半实物射频仿真实验室在实际工作中都发挥了重要的作用。半实物射频仿真系统处于微波暗室中,主要包括曲面状的天线阵列墙、三轴飞行转台、仿真控制系统等。在天线阵列墙上,以正三角形构型整齐排列多个辐射单元,相邻的3个单元构成一个三元组。在仿真系统工作时,三元组的3个单元可以同时工作,其辐射场在空中叠加,在转台处其合成辐射场的能流方向(或相位梯度方向)与真实环境下某个点目标的回波的能流方向相同,从而仿真了该方向的点目标[4]。改变3个单元的相对馈电幅度,就可以改变合成场的能流方向,从而可以对点目标在不同方位位置处及整个运动过程中的回波进行仿真。

三元组所仿真的点目标的方位位置可以使用幅度重心公式来表达[3]。根据不同的物理解释,幅度重心公式可以有不同的导出方法[5-6]。根据重心公式,仿真点目标的位置可以表达为三元组的3个单元位置的加权组合,其权重即为每个辐射单元的馈电幅度。幅度重心公式是一个简洁而又有一定近似程度的公式。其反映的是一种方位角度维的空间线性插值,通过空间中的3个单元,线性插值出待仿真的目标点。三元组的3个单元相当于空间采样点,因而在辐射单元附近,仿真误差较小。三元组的张角越小(即空间采样步长越小)，仿真精度越高。这是由于采样步长越小,线性插值的精确性越好。也就是说,当三元组的张角较大时,线性插值会存在较大误差,因而需要使用非线性插值。这就是三元组的近场效应和近场误差。关于三元组近场误差和近场修正的研究，已有多篇文献发表。文献[3]明确指出,此近场非彼近场,即三元组近场不同于单元近场。文献[7-8]认为,导引头接收到的3个单元发出的不同方向的平面波不能使用一个方向的平面波来替代,是产生三元组近场误差的原因。文献[9]研究了高精度毫米波系统的近场误差问题;文献[10]通过严格的电磁计算方法来研究三元组近场误差;文献[11]研究了复合阵列的近场误差变化规律;文献[12]通过函数拟合的方法进行了近场误差修正。对于存在不可忽略的三元组近场误差的仿真系统,通常需要建立修正表格,在仿真时加以矫正。在建立修正表格的过程中,可以采用不同的算法,以获得修正量。文献[13]通过计算雷达导引头的响应函数的梯度,来获得每次迭代所需要的修正量。文献[14]通过差分重心公式来获得每次迭代的修正量。差分重心公式的本质是通过增加一个点目标,把仿真偏离的点目标拉回,即增加的点目标与存在近场误差的仿真点目标的空间线性插值正好落在仿真点目标正确的方位。上述文献基本都集中于分析近场效应的产生原因和修正方法,而对于近场误差的各向异性却鲜有提及。实际上,在三元组张角逐渐增大的过程中,除了带来三元组近场效应,三元组结构的形状特性以及待测试雷达导引头的形状特性也将显现。这些在三元组被浓缩为一个点的情况下不会出现的问题将会被显现出来,导致三元组近场误差不一定随导引头自旋对称,即可能存在各向异性。雷达技术的精进对仿真精度提出了更高的要求,因而对三元组近场误差进行更深入的分析和处理是有必要的。

本文将对三元组近场效应进行研究,以改进馈电系数计算公式,降低三元组近场误差的影响，并对三元组近场误差的各向异性进行深入分析。本文在解析分析中,将单元天线在导引头处的辐射场按照平面波进行处理,而在藉以比较的数值计算中严格按照球面波处理。另外,文中所称导引头(口径面)旋转若非特别说明皆指绕纵轴旋转,即自旋。

为了聚焦问题,本文在分析中令三元组的3个单元进行了相位配平,且3个辐射单元在转台方向上的天线增益相同。

1 幅度重心公式及馈电系数的极坐标解

在半实物射频仿真的研究中,幅度重心公式具有重要的理论意义和实用价值。本文的研究也将在幅度重心公式的基础上展开。首先建立分析所用的坐标系[15],如图1所示。

图1 坐标系Fig.1 Coordinate system

以导引头的辐射口面中心点为坐标原点,建立xyz直角坐标系。其中,以雷达导引头的辐射口面为xy面,导引头天线阵列的两个正交的基线方向分别为x方向和y方向。三元组的3个单元的坐标为(xi,yi,zi)(zi≫xi,yi;i=1,2,3)。目标的坐标为(x,y,z)(z≫x,y;)与文献[16]相同,令

(1)

(2)

(3)

(4)

式中：Ci0(i=1,2,3)为第i个单元的由幅度重心公式给出的馈电系数,正比于各辐射单元的馈电电流大小。式(3)和式(4)为简单的线性方程组,其一个重要特点是具有对xy平面的旋转对称性。

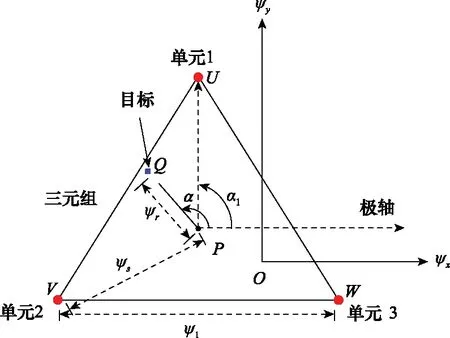
图2 二维角域坐标系Fig.2 Coordinate system in two-dimension angular domain

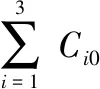
(5)

可以看到,馈电系数表达式只与目标在三元组中的相对位置有关,而与极角的绝对大小无关。由于极轴定义在导引头口径的天线基线上,因而导引头的旋转不影响重心公式的结果，馈电系数仅取决于待仿真目标点在三元组中的相对位置,而与导引头的旋转无关。这实际上是因为幅度重心公式的导出基于忽略导引头口面和三元组口径尺寸的影响,把其近似为点状,因而具有旋转对称性。另外,由于三元组结构是120°旋转对称的,当导引头口面固定时,Ci0关于目标的极角位置α具有120°的旋转对称性。

除了对称性分析,式(5)也给出了另外一种直观的认识。可以将(5)中的第一项视作零阶项,将第二项视作微扰项。很显然,第一项表达的是仿真点在三元组中心时的馈电系数,而微扰项相当于增加了另外一个仿真点,从而将仿真点从中心拉到正确的位置。此处显现的物理意义实际上与文献[14]讨论的差分重心公式具有一致性。

2 针对比相式单脉冲雷达的馈电系数修正

三元组相对于转台存在一定的张角,基于幅度重心公式给出的馈电系数将导致仿真结果存在三元组近场误差[3]。为了克服该误差,此处针对比相测向体制对馈电系数的计算进行修正。假设导引头口径面上有4个具有不同等效相位中心点的天线单元,其中，两幅天线单元在x方向上构成一幅干涉仪,另外两幅天线单元在y方向上构成一幅干涉仪。两个方向上的干涉基线长度分别为Lx和Ly，如图3所示。

图3 接收口径天线分布Fig.3 Antenna distribution in receiving aperture

将三元组各单元的相位依据其到O点的距离进行校准,即各单元到达O点的场同相位。三元组的各单元处于导引头口径的远场，则天线2和天线4接收到的三元组3个单元的辐射场分别为

(6)

(7)

式中：Ci为第i个单元的馈电系数。天线2和天线4接收到的目标的辐射场分别为

(8)

(9)

仿真环境下的天线口面场的相位信息应该等于实际环境下的天线口面场的相位信息,因而有

(10)

可得

(11)

式(11)的直观涵义是复信号叠加时,在相量图中,与最终合成结果方向垂直的部分合成为零。如图4所示,粉色的分量部分叠加为零。

图4 三元组单元辐射复信号相量合成图Fig.4 Phasor synthesis diagram of the complex signal radiated by the triad units

同理可得

(12)

(13)

(14)

可以使用式(13)和式(14)计算避免了三元组近场误差的馈电系数:

(15)

需要注意的是,式(15)中α和αi值的获取依赖于导引头口径天线基线取向,而当导引头可以三维自由转动时,α和αi值的获取是困难的,因此在实际工作中往往难以基于式(15)计算馈电系数。下面对该式进行展开分析。

令kLx/2=kLy/2=Γ。对sin函数做级数展开,只保留到三次项,并且注意到sin(α2+α3)=sin 2α1,通过推导可得第i个(i=1,2,3)单元的馈电系数为

(16)

其中

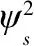
(17)

(18)

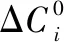
(19)

式(19)即为导引头旋转姿态未知时的馈电系数的最佳估计。

3 近场误差的各向异性

ΔCi随导引头的旋转而变,表明在不同的导引头口径面旋转姿态下,近场误差是不同的,即近场误差相对于导引头口面旋转而言存在各向异性。下面对其做详细分析:首先由馈电系数的差导出仿真位置的偏移量,即近场误差。

(20)

(21)

图5 三元组近场误差的分解Fig.5 Decomposition of the near field error of the triad

(22)

(23)

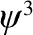
4 数值结果

采用如图1所示的坐标系。三元组的3个单元在初始xyz坐标系中的坐标为(0,0.2,15),(0.2 cos7/6π,0.2 sin 7/6π,15),(0.2 cos 11/6π,0.2 sin 11/6π,15),单位为m。工作频率为15 GHz。导引头口面天线基线长度Lx=Ly=0.2 m。

当目标方向处于三元组中心点时,对于仿真场景进行严格计算得出的仿真误差结果为1.0×10-4rad,而解析公式给出的结果为9.7×10-5rad,两个结果基本吻合。

分别基于式(5)、式(19)和式(15)给出的馈电系数进行仿真,并与真实目标方向比较,得出近场误差,如图6和图7所示。式(5)为重心公式的结果,式(19)为依赖导引头基线长度的结果,式(15)为需要依赖导引头旋转姿态的结果。图6为初始xyz坐标系下的结果,图7为xy面绕z轴顺时针旋转45°的结果。

从图6可以看到,图6(a)的近场误差最大,图6(c)的近场误差最小,但不为零,因为此时式(15)虽然摒除了三元组近场误差,但是单元相对于导引头口面的近场误差仍存在。图6(b)的近场误差虽然大于图6(c),但相对于图6(a)仍有显著的降低。图7有相同的规律。因此,基于式(19)的馈电系数的计算,有助于克服传统幅度重心公式计算所带来的三元组近场误差。图6(b)和图7(b)中的误差实际上是图5中的可变量部分,当导引头旋转角未知时,该误差是不可修正的。因此,式(15)给出的馈电系数是导引头自旋姿态可知时的最优解,而式(19)给出的馈电系数是导引头自旋姿态未知时的最优解。

对比图6(a)和图7(a)可知,在三元组内的误差幅度分布图存在差异,这是因为图5所示的4个分量叠加后的幅度随导引头自旋而变;对比图6(b)和图7(b)可知,在三元组内的误差幅度分布图相同,这是因为图5所示的两个可变分量的角度差固定,叠加后的幅度不随导引头旋转而变。这些结果都与前述各向异性分析结果吻合。此外,由图6和图7可以看出,式(19)给出的结果比式(5)给出的结果对某些区域的近场误差可以改善一个数量级;式(15)给出的结果比式(19)给出的结果对某些区域的近场误差可以改善两个数量级。式(5)对应的近场误差来源于三元组近场和单元近场;式(15)对应的近场误差来源于三元组近场的确定部分和单元近场;式(15)对应的近场误差仅来源于单元近场。

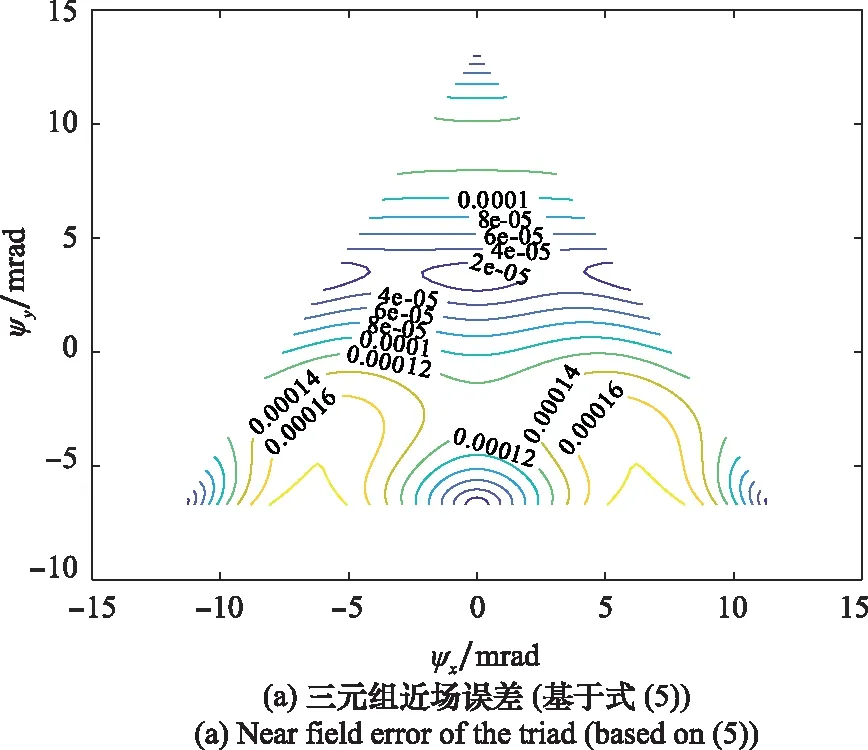
图6 旋转角为零时各种馈电系数下仿真的近场误差Fig.6 Near field error with different feeding coefficients when the rotation angle is zero

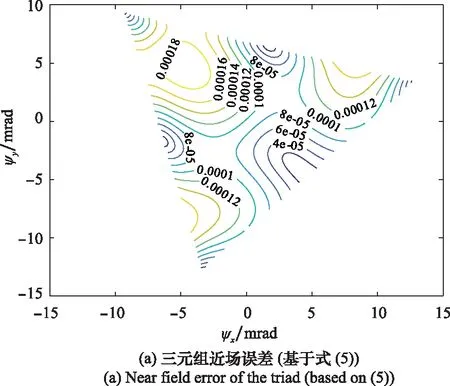
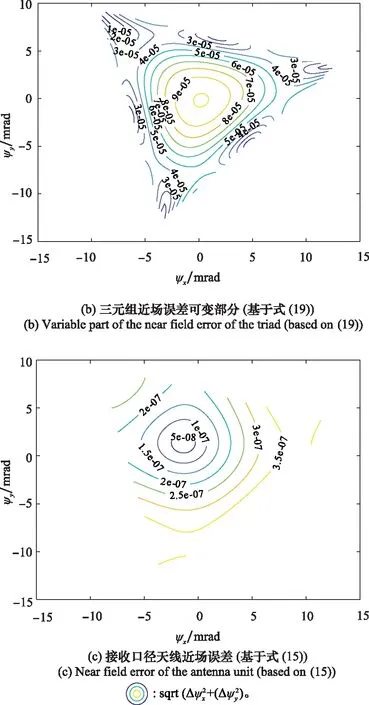
图7 旋转角为顺时针45°时各种馈电系数下仿真的近场误差Fig.7 Near field error with different feeding coefficients when the rotation angle is 45°

实际上,图6(b)和图7(b)给出的即为导引头旋转姿态未知时不可修正的近场误差的大小。

5 结 论

本文在二维角度域的极坐标系下研究了比相式单脉冲雷达的半实物射频仿真的三元组近场效应问题,给出了可以克服三元组近场误差的馈电系数的表达式。该馈电系数表达式可以不依赖于对导引头口径面旋转姿态的掌握。此外,为了分析三元组近场误差的各向异性,给出了三元组近场误差的解析表达式。结果表明,比相式单脉冲雷达的三元组近场误差包括两个部分,一部分随着导引头自旋保持不变,而另一部分则会随着导引头自旋而改变,从而导致了三元组近场误差的各向异性特性。且当导引头旋转姿态未知时,存在不可修正的近场误差大小,即随导引头旋转可变的部分。数值实验证实了这些分析结果。本文针对的是比相式单脉冲雷达,在后续的工作中将在此基础上继续对比幅式单脉冲雷达的三元组近场误差的各向异性特性展开研究。