无人机集群分组编队控制跟踪一体化设计

张 毅, 于 浩, 杨秀霞, 姜子劼

(海军航空大学, 山东 烟台 264001)

0 引 言

近年来,无人机(unmanned aerial vehicle, UAV)因其独特的优势被广泛应用于军事和民用领域。单架UAV因机载传感器的限制,难以执行复杂作战任务,而由多UAV组成的编队兼具各架UAV的性能优势,显著提高了系统的容错率和作战效能[1-4],已成为当前研究的热点。编队控制技术也随之取得了长足的发展,经典的编队控制方法包括:领导-跟随法[5-6]、虚拟结构法[7-8]、基于行为法[9-11],而上述3种编队控制方法均存在一定的缺陷。其中,领导-跟随法受编队结构的约束,存在编队容错率较低的缺点;虚拟结构法描述的编队队形相对固定且计算量大;基于行为法难以用数学方法描述UAV的具体行为,不利于系统的稳定性分析。

一致性编队控制方法采用分布式的通信拓扑结构描述编队内各成员的信息交互,对全局信息的依赖性显著降低,具有编队扩展性强、稳定性好的优势。随着该理论的应用和发展,国内外学者对于分布式编队的研究愈加深入[12-13]。Ren[14]设计了一致性编队控制协议,实现了对微型UAV编队的控制,并指出前3种编队控制方法均可在一致性编队控制的框架下得到统一。Kang等[15]研究了时变编队的鲁棒控制问题,基于智能体邻接信息设计控制器,使编队在跟踪预定轨迹的同时能够保持较好的抗干扰性能。Dong等[16-18]研究了UAV集群时变编队控制问题和编队包含控制问题,并在实验平台进行了验证。符小卫等[19]针对动态障碍物的规避问题,结合一致性理论和人工势场法设计了控制律,实现了障碍环境下的分布式队形控制。Liu等[20]对含时滞约束的多智能体编队控制问题进行了研究,更加符合现实意义。

需要指出的是,上述文献仅对单一编队的控制进行了研究。然而,在多目标围捕、协同饱和攻击、多目标协同搜索等实际作战场景中,单个编队无法协同高效地完成作战任务。此时,需要将系统分为多个编队,并通过编队间的相互配合,发挥系统的整体效能。

目前,对于多编队控制问题的研究成果较少,且由于涉及编队内部及编队间的相互协同,相关研究更具有挑战性。国内外学者大都基于多一致性的编队控制方法进行研究。Dong等[21]最早将多一致性理论应用到编队控制问题中,研究了有向通信拓扑下的一般线性多智能体系统的时变多编队控制问题,但各个编队是相对孤立的个体,缺乏编队间的相互协同。Han等[22]分别针对固定拓扑和切换拓扑设计了多编队控制协议,但从仿真结果来看,在完成编队分组后,组内智能体只是被动地跟踪领导者,同样缺乏编队间的信息交互。田磊等[23-24]分别对同构和异构智能体系统的分组编队跟踪控制问题进行了研究,实现了分组编队的协同配合。另外,Chen和王祥科等[25-26]为解决大规模UAV集群的控制问题,基于领导-跟随的编队结构提出了一种分布式多编队分层控制架构,分别设计了长机层和僚机层的控制律,领导者通过跟踪期望航路点实现编队之间的分组协同,跟随者跟踪所属编队的领导者协同完成共同的子任务,进而实现了整个集群的协同控制。

受上述文献启发,为解决UAV多编队在有向通信拓扑下的协同控制问题,本文基于参数组的队形描述方法,提出了一种满足组内组间协同的UAV多编队跟踪控制算法。相较于文献[23-26],本文提出的控制策略更加注重编队之间以及编队内部各UAV之间的协同,能够克服上述控制方法因队形向量固定致使集群分组队形难以变换的缺陷,确保集群队形变换更加灵活。首先,建立分层双虚拟控制结构,分别在顶层和底层的控制架构中设置基准UAV,以轨迹UAV为中心实现组内和组间队形的协同变换,并结合一致性控制理论设计了基于邻接误差的编队控制律,同时给出了系统稳定的条件;其次,设计了以目标跟踪为导向、编队控制为基础的分组编队目标跟踪控制一体化设计方案,将顶层编队的目标跟踪细化为两个子任务:一是集群领导者对机动目标的跟踪,二是编队之间的协同控制,从而实现了编队控制与目标轨迹跟踪的一体化设计,克服了传统目标跟踪方法相位调整时间长的缺陷;最后,仿真结果证实了本文控制律设计的有效性。

1 预备知识和问题描述

1.1 图论

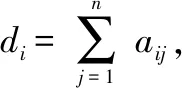
假设1对于UAV集群系统中的每个编队而言,均存在以编队领导者为根节点的有向生成树,且跟随者之间以及编队领导者之间均可视为双向通信。

引理1在假设1成立的条件下,若至少存在一个跟随者与编队领导者相连,则矩阵L+γb′是正定的[27-28]。

引理2在假设1成立的条件下,对所有x∈Rn,λmax(Ll)xTx≥xTLlx≥λmin(Ll)xTx成立,其中λmax(Ll)和λmin(Ll)分别为Ll的最大特征值和最小特征值[29]。

1.2 分组编队控制架构

针对UAV集群分组编队跟踪控制问题,建立由集群领导者、编队领导者和编队跟随者组成的分层协同控制框架,具体结构如图1所示。与文献[23-25]中的控制方案不同,本文在顶层和底层编队内分别设置轨迹导引UAV和基准UAV,以实现集群的协同,该控制架构采用并行的分布式通信结构,为大规模UAV集群的分组编队协同控制提供了可行方案。

集群领导者:包括2架虚拟无人机UAVp和UAVb,其中UAVp决定整个集群的运动轨迹,UAVb为各编组间的相位协同提供基准,集群领导者只单向传输信息给编队领导者,不接收其他任何UAV的信息。

编队领导者:每个编队内包括真实领导者UAV0和虚拟领导者UAVb′,其中UAV0负责导引该编队的飞行轨迹,UAVb′为该分组内UAV提供相位基准,其他成员为跟随者,编队领导者UAV0不接收跟随者的信息,只接收来自集群领导者和其他编队领导者的信息,跟随者只接收来自其所在分组中编队领导者和其他跟随者的信息。

图1 UAV集群控制架构Fig.1 Control architecture of UAV swarm

对于基准UAV的功能,本文将在第2节结合图2做详细说明。为方便描述,后文提到的集群领导者和编队领导者均指轨迹导引无人机UAVp和UAV0。

1.3 模型建立

考虑由n架UAV组成的集群系统,通信拓扑可以用有向图来描述。传统线性模型难以准确刻画UAV的非线性本质,为确保模型的精确性,参考文献[30],本文以旋翼UAV为研究对象,采用带有Lipschitz项的非线性模型来描述UAV的动力学模型。

(1)

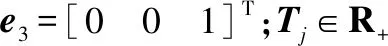
式中:μ>0是一个常数。

本文在研究编队分组控制时,主要关注UAV的位置和速度变化,因此忽略了内环姿态控制的影响,定义辅助控制量uj(t)∈Rd:

(2)

则式(1)中的动力学模型可改写为

(3)

同时,为满足实际条件,设置UAV的飞行速度满足如下约束:

集群领导者UAVp的动态模型可表示为如下形式:

(4)

式中:pp(t)、vp(t)分别表示t时刻集群领导者UAVp的位置和速度;up(t)是控制输入量,决定整个集群的状态轨迹。

虚拟领导者UAVb和UAVb′分别为编队领导者之间和编队跟随者之间提供相位基准,两者的动态模型可描述为

(5)

式中:pk、vk和uk分别表示UAVk的基准向量、基准变化量和基准控制量;k∈{b,b′}。需要注意的是,uk为预定参数,pk和vk受uk的控制,pk和vk在此作为队形参数归一化后的位置和速度。

假设整个集群被划分为m(m≥1)个编队,则根据图1所示的架构,系统中包括:1个集群领导者UAVp和虚拟领导者UAVb,m个编队领导者UAV0和虚拟领导者UAVb′,n个跟随者。为方便理解图1所示的控制架构,下面分别对编队内部和编队之间的通信拓扑进行描述。

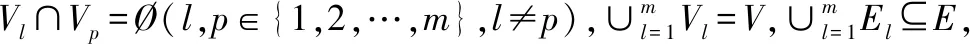
据此,系统中所有真实UAV的邻接矩阵可描述为

式中:矩阵A的对角元素(矩阵)表示编队内部各UAV之间的通信关系,而非对角元素(矩阵)为编队之间的信息交互,即编队领导者之间的通信。

2 集群编队队形描述

图1对集群宏观层面的控制策略进行了描述,下面给出编队之间和编队内部UAV之间的具体控制策略。首先以某一底层编队为例,通过构造队形参数组,实现基于平移、缩放和旋转3种基本运动的编队控制:

T(N)={p0(t),pb′(t),C1(t),…,Cnl(t)}

(6)

Ci(t)=ri(t)Ri(t),i∈{1,2,…,nl}

(7)

式中:p0为编队领导者的位置,其作为编队中心,决定编队的空间位置,而不影响编队的几何构型;ri≥0为缩放参数,表示UAVi到编队中心p0的距离;Ri∈SO(2)为旋转参数,表示由当前位置到期望位置的旋转变换矩阵。缩放运动与旋转运动都是相对UAVb′而言的,两者共同决定了编队的几何构型。

式(6)的参数组T(N)包含了所定义的期望编队队形的诸个要素,下面给出基于队形参数组的UAV编队控制问题的具体定义。

定义1对于底层编队中任意跟随者的初始状态,若满足

(8)

则称实现了对底层编队期望队形的控制。式中,hi(t)=p0(t)+Ci(t)pb′(t),表示期望的编队队形,具体可描述为:各跟随者到达以编队领导者为中心、以虚拟领导者为基准的期望位置。

考虑

pb′(t)=[cos(θb′(t)) sin(θb′(t))]T

(9)

(10)

基于参数组编队队形的具体描述如图2所示。

图2 编队队形描述示意图Fig.2 Schematic diagram of formation description

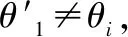
如图3所示,编队之间的协同与编队内部UAV之间的协同类似,不同之处在于集群领导者作为控制集群飞行的中心,而各编队领导者作为跟随者,以UAVb为基准实现相位协同。

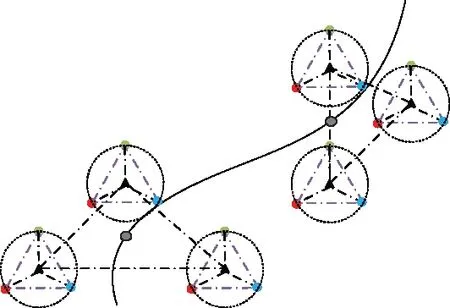
图3 多编队协同示意图Fig.3 Schematic diagram of multi-formation cooperation

此时,队形参数组和队形控制定义均有所改变。

(11)

(12)

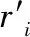
定义2对于顶层编队中任意编队领导者的初始状态,若满足:

(13)

另外,如图4所示,通过队形参数组的合理设计,可实现由多分组编队到单一编队的切换,用于执行目标围捕、协同饱和攻击等对UAV数量要求较高的复杂任务。

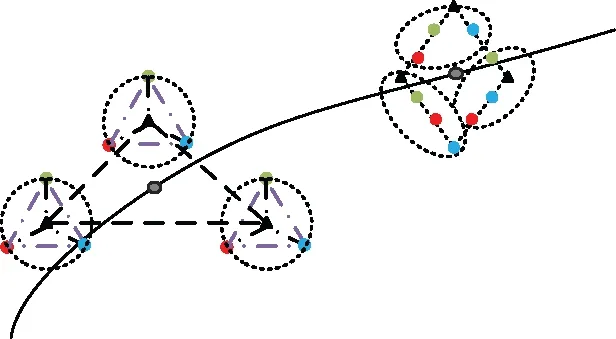
图4 多分组编队切换为菱形编队Fig.4 Switching from multi-group formation to diamond formation

基于上述控制策略,通过对两组队形参数的合理设计,能够实现编队内部各UAV之间的协同,并确保各编队之间的相互联系、密切协作,进而为组内组间集群队形协同变换创建基础。

3 控制律设计

为实现整个UAV集群的协同控制,分别对底层编队和顶层编队进行控制律设计。其中,顶层编队既要实现编队领导者之间的协同,又要确保对目标的精确跟踪,为使整体效能最大,设计编队控制与目标跟踪一体化的控制策略。

3.1 底层编队控制律设计

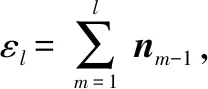
(14)

求导可得编队l的速度误差为

(15)

定义3对于任意编队l,给定任意初始状态,若满足:

则称编队内的无人机能够实现期望的编队队形并保持。式中,hij(t)=hi(t)-hj(t)。

对编队跟随者设计基于邻居UAV误差信息的编队控制律:

(16)

式中:aij为对角矩阵A中的元素;k为控制增益;μ为Lipschitz常数;⊗表示克罗内克尔积;In表示元素全部为1的n维列向量。

定理1对于任意底层编队l,如果控制增益k满足:

(17)

则称在队形参数组和编队控制律(16)的作用下,UAV编队形成期望的编队队形。

证明分别对式(14)和式(15)求导,进一步可得误差方程:

(18)

编队误差方程可转化为

(19)

由此,将编队控制问题转化为闭环系统的稳定性问题。定义具有如下形式的Lyapunov函数:

Vl(t)=

(20)

下面证明Vl(t)的正定性:

(21)

即有:

(22)

由克罗内克尔积的性质:

(1) (A⊗B)(C⊗D)=AC⊗BD;

(2) (A⊗B)-1=(A-1⊗B-1);

可得

(23)

则有

(24)

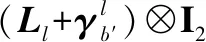
Vl(t)对时间求导可得

(25)

根据Lipschitz条件可得

(26)

根据引理2可得

(27)

证毕

3.2 顶层编队控制律设计

对于顶层编队的跟踪任务而言,集群领导者只需在采样时刻持续不断地对目标实施追踪,各编队领导者以集群领导者为中心,在基准UAV的作用下保持相位协同即可完成对机动目标的跟踪,克服了传统跟踪算法放弃了在UAV运动至跟踪过程中对相位调整的机会、从而导致相位调整时间较长的问题。由此,顶层编队的目标跟踪控制可具体细化为:① 集群领导者对机动目标的跟踪;② 编队领导者之间的协同控制。

3.2.1 目标跟踪策略设计

假设目标的机动形式未知而其运动状态在每个采样时刻均是可测的,则可在每个采样时刻,根据目标的运动状态调整UAVp的运动方向,使其不断趋近目标的位置,直至与目标重合。顶层编队跟踪目标轨迹如图5所示。

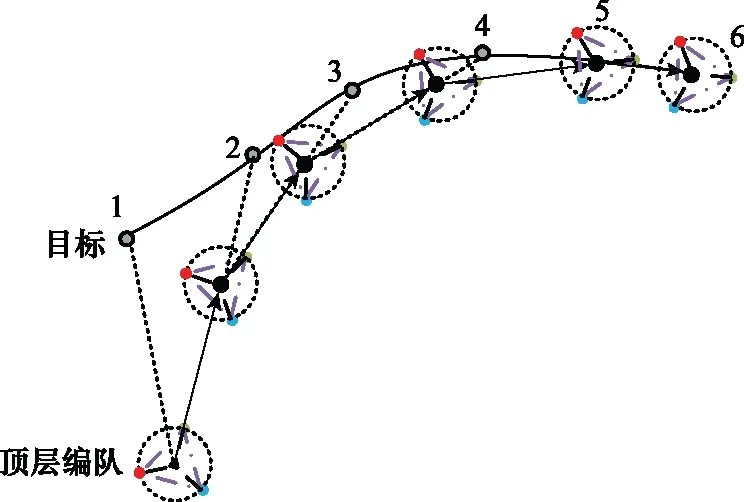
图5 顶层编队跟踪目标轨迹Fig.5 Top formation tracking target trajectory

跟踪过程可描述如下:

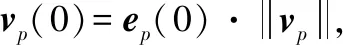
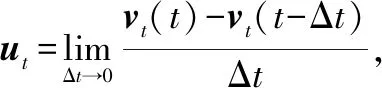
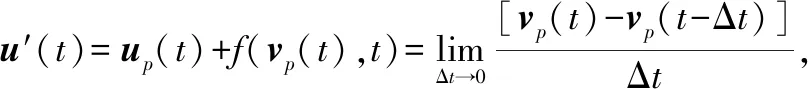
步骤4重复步骤2～步骤3,直至UAVp跟踪上目标。

3.2.2 顶层编队控制律设计

分别定义顶层编队的速度误差及位置误差:

(28)

(29)

定义4对于整个集群编队,给定任意初始状态,若存在某一有界时刻t0,使得当t≥t0时,满足:

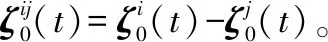
参照式(14),设计顶层编队控制律为

(30)

定理2对于顶层编队,如果控制增益k满足：

(31)

则称在队形参数组和控制律(30)的作用下,期望的顶层编队队形生成并保持。

证明过程参照定理1,在此不再赘述。

4 仿真验证

为验证本文提出的集群控制架构和控制算法设计的有效性,设置仿真场景如下:

如图6所示为集群通信拓扑结构,集群由20架UAV组成,其中包括4个编队领导者和16个跟随者,0、b和bi分别表示集群领导者UAVp、虚拟领导者UAVb和虚拟领导者UAVb′。

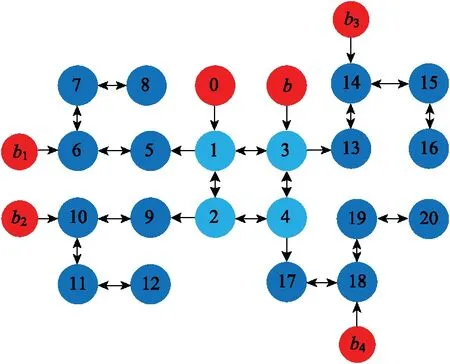
图6 集群通信拓扑结构Fig.6 Communication topology of swarm

设集群领导者的Lipschitz非线性项为

编队领导者和跟随者的Lipschitz非线性项为

即Lipschitz常数μ=0.1。

为满足系统稳定条件,令控制增益k=1.5。为验证控制效果,设置不同时刻的集群队形参数和编队队形参数如表1、表2所示,分别决定顶层编队和底层编队的期望队形。为方便表述,令θ′i表示θ′1=θ′2=θ′3=θ′4，ri表示r1=r2=r3=r4。

表1 集群队形参数

表2 编队队形参数

设定UAV的速度和加速度约束如表3所示。

表3 速度和加速度约束

编队领导者的初始条件如表4所示,跟随者的位置和速度在满足飞行约束条件下随机生成。

表4 编队领导者的初始条件

4.1 分组编队控制仿真

任意取定集群领导者加速度,对集群分组编队控制算法进行验证。取定的加速度为

图7表示不同时刻的集群运动轨迹,通过队形参数组的设置,各编队以集群领导者为中心,在不同时刻形成期望队形,图中形状相同的为同一组别的UAV,实线标注的为编队领导者的运动轨迹,黑色虚线标注的形状表示当前时刻的集群构型。从图7中可以看出:t=9 s集群为方形,t=19 s集群已变换为菱形,t=29 s时集群已完成由多编队到单一编队的切换。

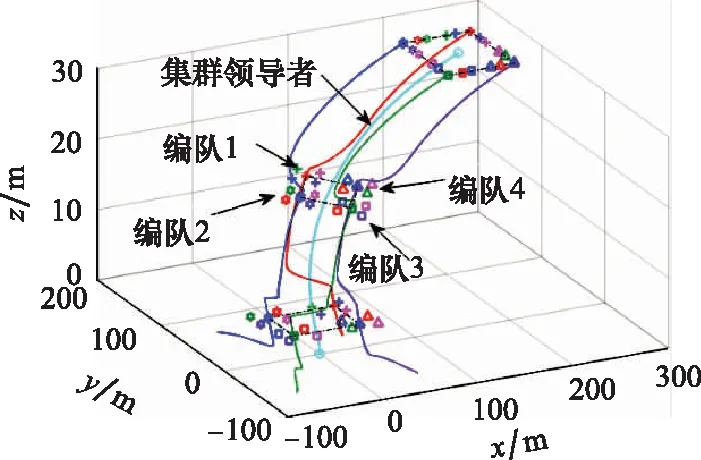
图7 不同时刻(9 s、19 s、29 s)的集群运动轨迹Fig.7 Swarm trajectories at 9 s, 19 s and 29 s

由于仿真中UAV数量较多,为方便阅读,仅将编队领导者和集群领导者的运动轨迹标注至图7中。

由图8和图9可知,在5s左右,集群完成期望的多编队分组,速度和位置误差均趋于零,而随着队形参数的改变,在t=10 s、t=20 s时误差出现波动,随后在控制律作用下很快趋于零。图10和图11展示了底层编队的位置和速度误差,可知编队层面的位置和速度误差均能够实现快速收敛。由仿真结果可知,在实现编队之间协同变换的同时,编队内部各UAV也能够按照预设参数实现队形变换,显然控制律的设计满足期望的控制要求。

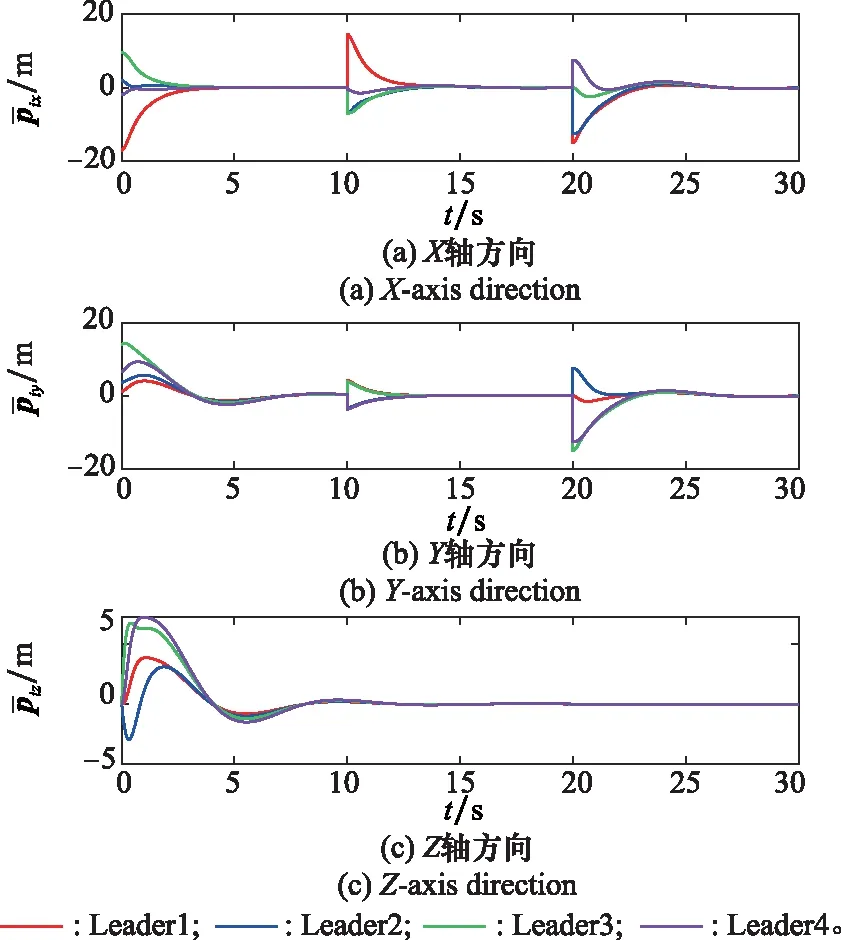
图8 顶层编队位置误差Fig.8 Position error of top formation

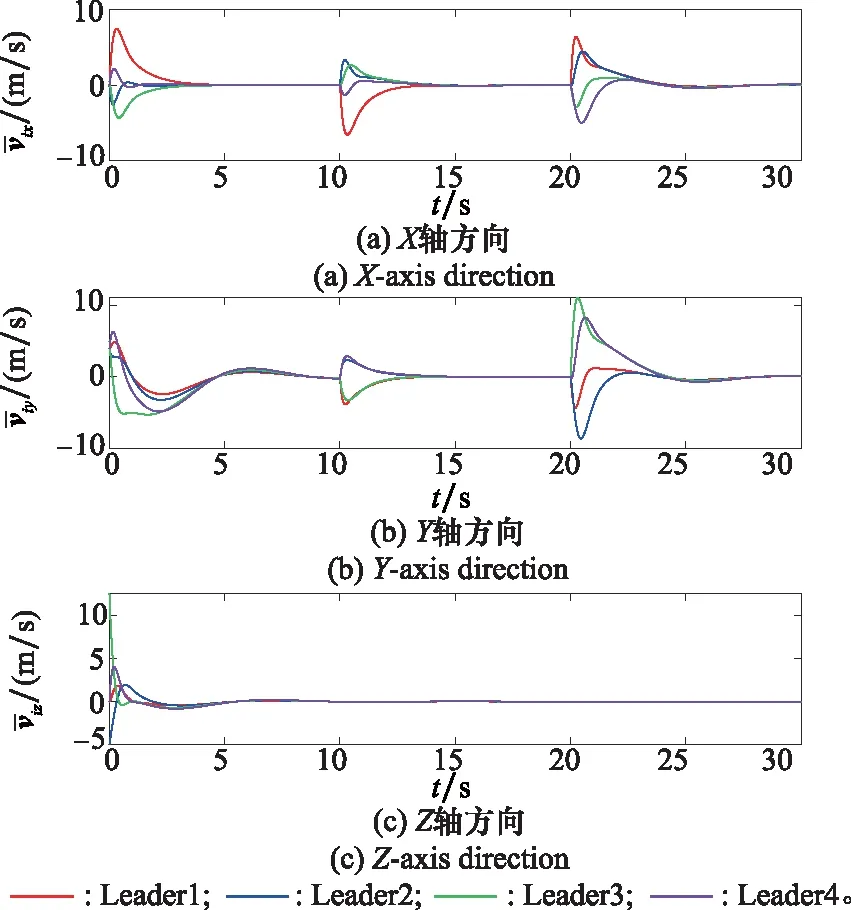
图9 顶层编队速度误差Fig.9 Velocity error of top formation

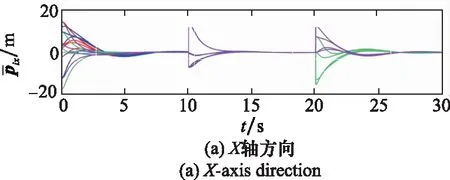
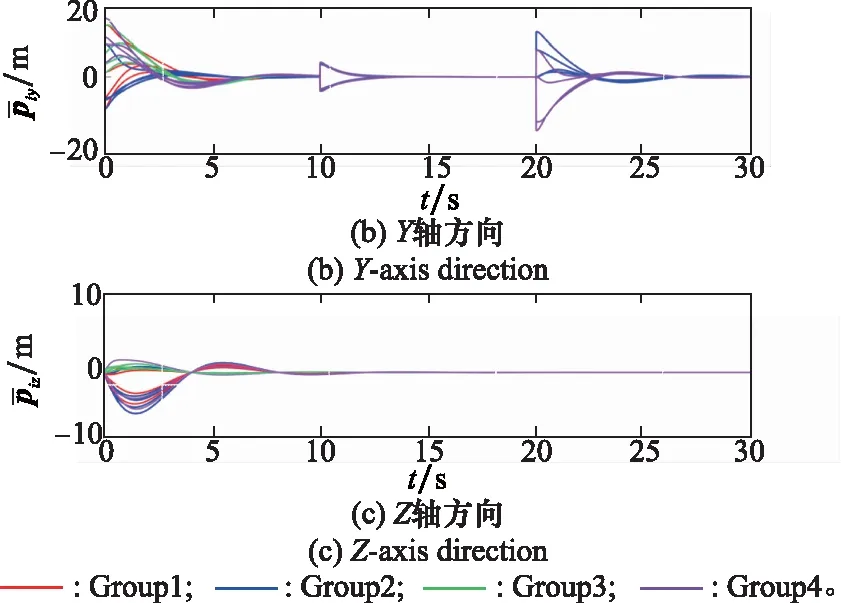
图10 底层编队位置误差Fig.10 Position error of bottom formation

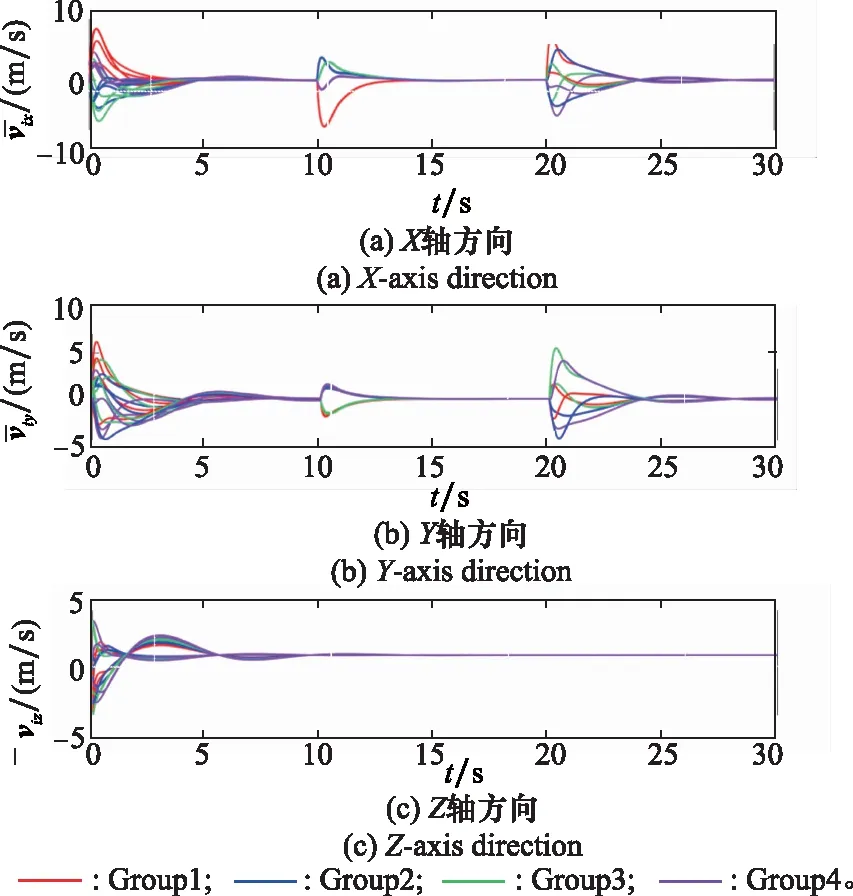
图11 底层编队速度误差Fig.11 Velocity error of bottom formation

4.2 分组编队控制仿真对比

为进一步验证本文控制策略设计的优势,将本文的一致性分组编队控制算法与文献[22]的方法进行对比,设置UAV的初始条件如表5所示,仿真结果如图12所示。

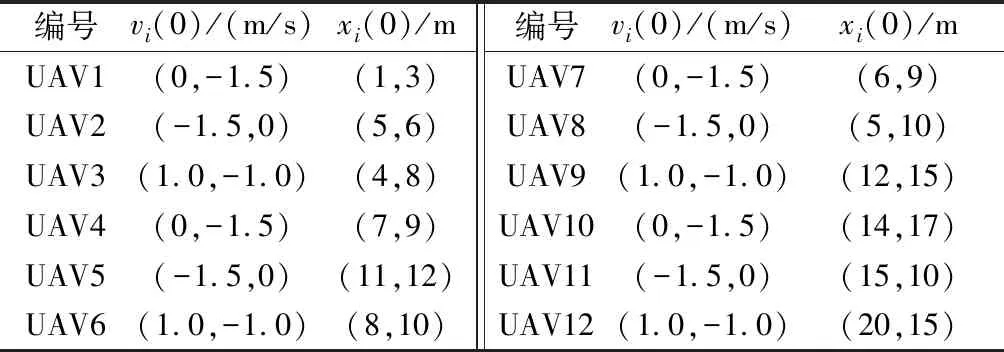
表5 文献[22]仿真初始条件

从文献[22]方法的仿真结果可以看出,UAV集群能够按照预定的期望分组形成多编队,但各编队到达稳定状态后,仅在编队领导者的轨迹引导作用下飞行,编队间缺乏组间协同,致使编队队形相对固定,无法完成队形变换等任务。从图7可以看出,本文设计的控制算法包含队形参数组的反馈项,能够在实现速度一致目标的同时,实现编队之间的相互协同,更加符合现实需求。

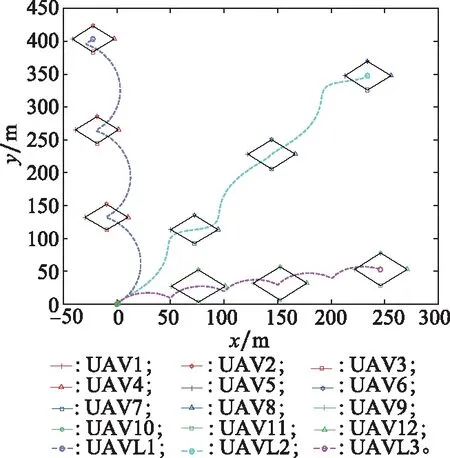
图12 文献[22]方法仿真结果Fig.12 Simulation result of the method in [22]

4.3 分组编队目标跟踪一体化控制仿真

为验证集群对机动目标的跟踪效果,设目标的初始位置为pt=(-50,50,0)m,目标的加速度为

队形参数、控制增益等初始条件保持不变,跟踪过程如图13所示，跟踪误差如图14所示。

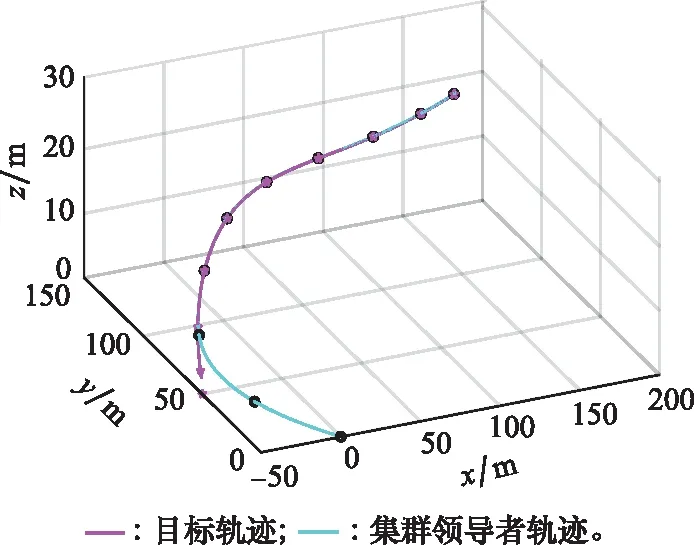
图13 集群领导者跟踪目标的虚拟轨迹Fig.13 Virtual trajectory of swarm leader tracking target

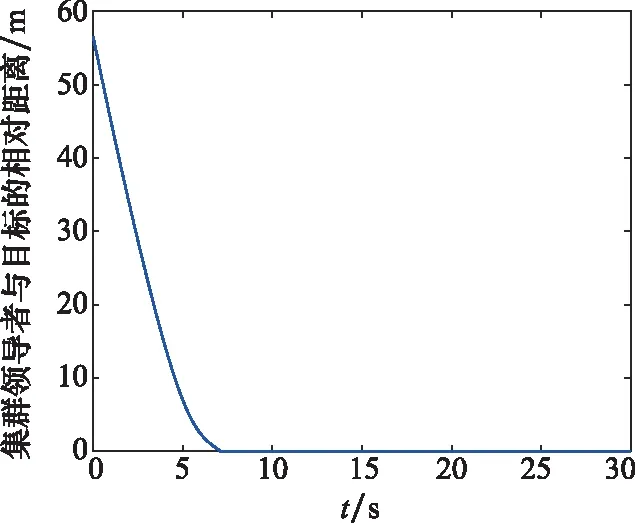
图14 集群领导者与目标的相对距离Fig.14 Relative distance between swarm leader and target

从图13和图14可知,集群领导者实现了对机动目标的精确跟踪,误差在跟踪策略的作用下收敛为零,表明跟踪算法的设计符合控制要求;从图15可以看出,整个系统在集群领导者和编队领导者的双重作用下,实现了对目标轨迹的有效跟踪。通过仿真,直观描述了集群领导者和编队领导者分别对集群和编队轨迹的引导作用。

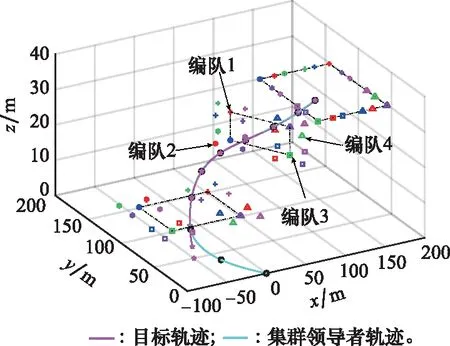
图15 集群目标跟踪轨迹Fig.15 Target tracking trajectory of swarm

5 结束语

本文针对UAV集群多编队的协同控制问题,提出了一种满足组间协同配合的UAV多编队跟踪控制一体化算法。在含Lipschitz非线性动力学项的UAV模型的基础上,建立了具有双虚拟结构的分层分组控制结构,并结合一致性理论设计了编队控制律,实现了集群组内和组间队形的协同变换;将顶层编队的跟踪任务细化为编队控制、目标跟踪的一体化控制方案;最后,通过仿真证实了控制律设计的有效性。在后续的研究工作中,将考虑多编队在障碍环境以及多目标跟踪等复杂任务背景下的协同控制问题。