融合梯度信息自适应窗口的立体匹配

陈嘉明，罗亚波

（武汉理工大学 机电工程学院，武汉 430070）

双目立体视觉近年来在三维重建、视觉导航、医疗诊断等领域中取得应用[1-2]。使用双目立体视觉[3]将包含更多的三维信息并具有成本低、实现难度低的优点。立体匹配精度是三维重建效果的决定因素，通过设定规则获得稠密视差并转化为深度作为三维重建的基础。现有的立体匹配算法仍然存在许多缺陷，如弱纹理区域以及重复纹理区域有大量误匹配点，如遮挡区域的误匹配问题，以及在深度不连续区域匹配效果不佳等问题。

局部立体匹配算法研究包括根据邻域信息选择合适窗口，如自适应窗口算法[4]、多种匹配算法设定不同权值获得具体窗口、对图像进行分割并将分割所得小区域[5]作为匹配基元的匹配算法等。

1 双目立体视觉

1.1 立体匹配算法

根据相机标定求得相机的内外参数并对左右相机进行立体校正使得左右成像平面符合极线约束。校正完成后以左图为基准，设计步骤从右图中寻找对应点并计算列差值，即视差d。立体匹配算法步骤如图1所示[6]。

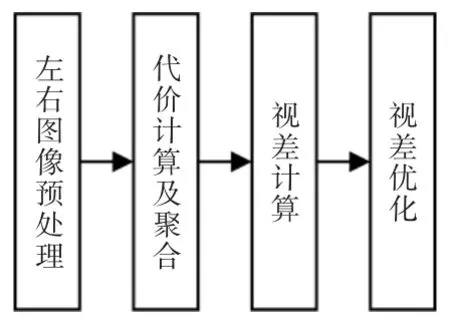
图1 立体匹配算法步骤Fig.1 Steps of stereo matching algorithm

图像需进行滤波处理进行噪声去除，常用的滤波方法有高斯双边滤波、中值滤波、直方图均衡滤波[7]。基于像素点的匹配代价主要通过灰度值、梯度等信息进行计算，计算结果作为相似性的度量。常用的2 种代价计算方法分别为AD（absolute differences）变换和Census 变换，AD 变换算法为

式中：CAD（x，y，d）为左图像选定点和右图像待匹配点的匹配代价；IL（x，y）为左图像选定点的灰度值；IR（x，y-d）为右图像中待匹配点的灰度值。

Census 变换分别通过邻域像素与中心像素的灰度值比较计算出左图像编码及右图像视差为d 的编码，求出汉明距离作为视差d 的匹配代价。Census变换[8]示例如图2所示。

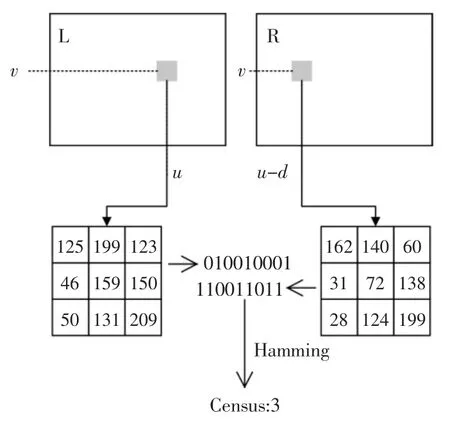
图2 Census 变换示例图Fig.2 Example of Census transform

AD-Census 立体匹配融合2 种变换结果作为视差d 对应的初始匹配代价。代价聚合环节采用十字交叉法构造十字交叉域，并以设定的规则将窗口内代价值聚合到中心点的初始代价上，以聚合代价作为视差d 最终的匹配代价值。

视差计算环节采用WTA（winners takes all）算法[9]，选择匹配代价最小的视差值作为结果。通过左右一致性法剔除错误匹配点，在遮挡区内利用背景信息进行错误点填充，非遮挡区内选择颜色相近像素的视差值进行填充。

1.2 实验测试数据及平台

实验所用的标准测试图像集来自网站（https：//vision.middlebury.edu/），本文采用Cones，Cloth，Teddy和Rocks 4 组图像。以实验结果图与真实视差图差值作为评判标准，若同一点视差差值小于1 则判定为匹配正确点，反之判定为误匹配点，并将视差图分为三类区域：全区域（all）、深度不连续区域（disc）和非遮挡区域（nonocc）。

实验测试平台：3.6 GHz Ryzen 5 3600，16 GB内存，系统为Window 10，软件环境为Spyder（Anaconda3）+OpenCv 3.4.1。

2 自适应窗口

2.1 匹配窗口的影响

采用SGM（semi-global matching）立体匹配算法[10]对测试图像进行实验，增大窗口并记录算法误匹配率和运行时间。实验均采取正方形窗，窗口大小为（2N+1）2，N 为自然数。误匹配率和运行时间如图3和图4所示。

图3可以看出随着窗口增大，在Teddy 和Cones图像中全区域误匹配率均不断下降，其中当窗口大小从3×3 扩大到13×13 时Rocks 图像中的全区域误匹配率从19.63%下降至13.86%。图4可以看出算法运行时间随着窗口增大而逐渐增加。对Teddy图像集，运行时间从1.42 s 增加到4.03 s。

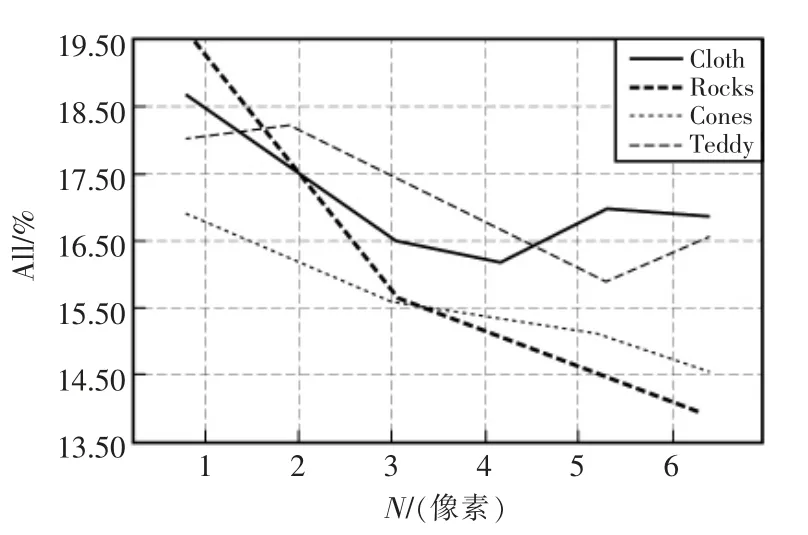
图3 SGM 算法误匹配率Fig.3 Mismatch rate of SGM algorithm

图4 SGM 算法运行时间Fig.4 Running time of SGM algorithm

通过该实验可以分析出，窗口过小会导致误匹配率上升；窗口过大可以提升算法精度，但会导致运行时间大幅增加。设想对于每一个像素点都有对于自身匹配效果最好的窗口大小，进而引出根据领域信息调节自身窗口大小的自适应算法[11]。

2.2 融合梯度信息的自适应窗口算法

同一物体表面或背景在成像平面上具有颜色相似性，而在边缘区域因深度变化而导致视差图的灰度值会出现大幅度的变化，因此对具有不同特点的区域应采用不同大小的窗口[12]。

在代价计算前先采用Sobel 算子[13]求出左图分别在x，y 方向上的梯度值，梯度幅值计算公式如下：

式中：m（i，j）为点（i，j）的梯度幅值；gx和gy分别为在x，y 方向上的梯度值。同一物体或背景表面上的梯度幅值通常较小；而在边缘区域深度变化剧烈而导致梯度值变大。梯度幅值图直方统计图如图5所示。

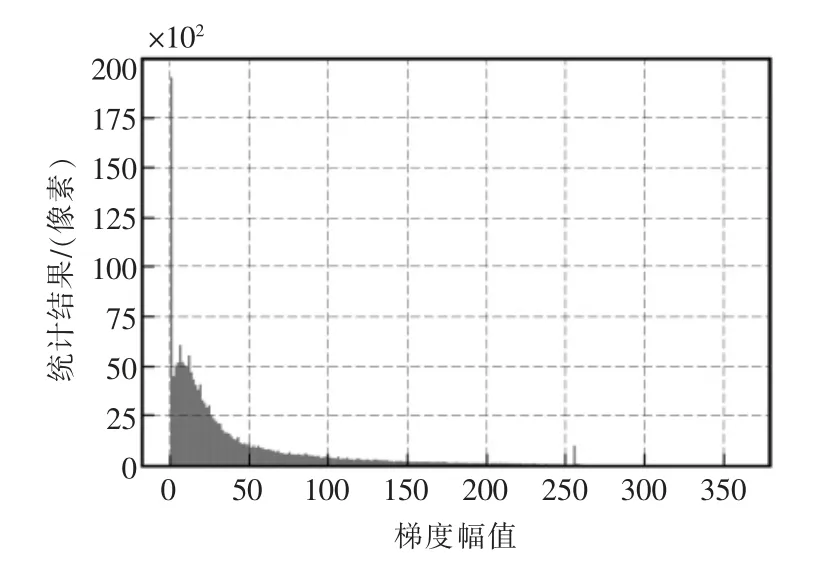
图5 Cones 图像梯度幅值直方图Fig.5 Histogram of gradient magnitude

图5可以发现Cones 图像中含有大量梯度幅值为0 的点，可以推测该类点为弱纹理区域。使用Canny 算子提取图像的边缘并统计边缘点数，当大于某个梯度幅值时的点个数等于边缘点数时，选定该梯度幅值为阈值T1。当梯度幅值大于T1时，该点为边缘点，因此采用最小的3×3 窗口；当梯度幅值大于1 且小于T1时为边缘附近区域，采用窗口大小为5×5；当梯度幅值小于1 时判断该点为弱纹理区域点，对于弱纹理区域由于深度变化不明显，可以继续扩大窗口以获取更多的信息，信息差计算公式如下：

式中：μ 为均值；N 为当前窗口内像素总数；m 为当前点的梯度幅值大小；（i，j）为当前点坐标；x，y 为窗口内点与当前点的相对坐标；d 为当前视差；M 为当前窗口。当μ 小于阈值T2时，扩大窗口以获取更多的信息，自适应窗口算法流程如图6所示。

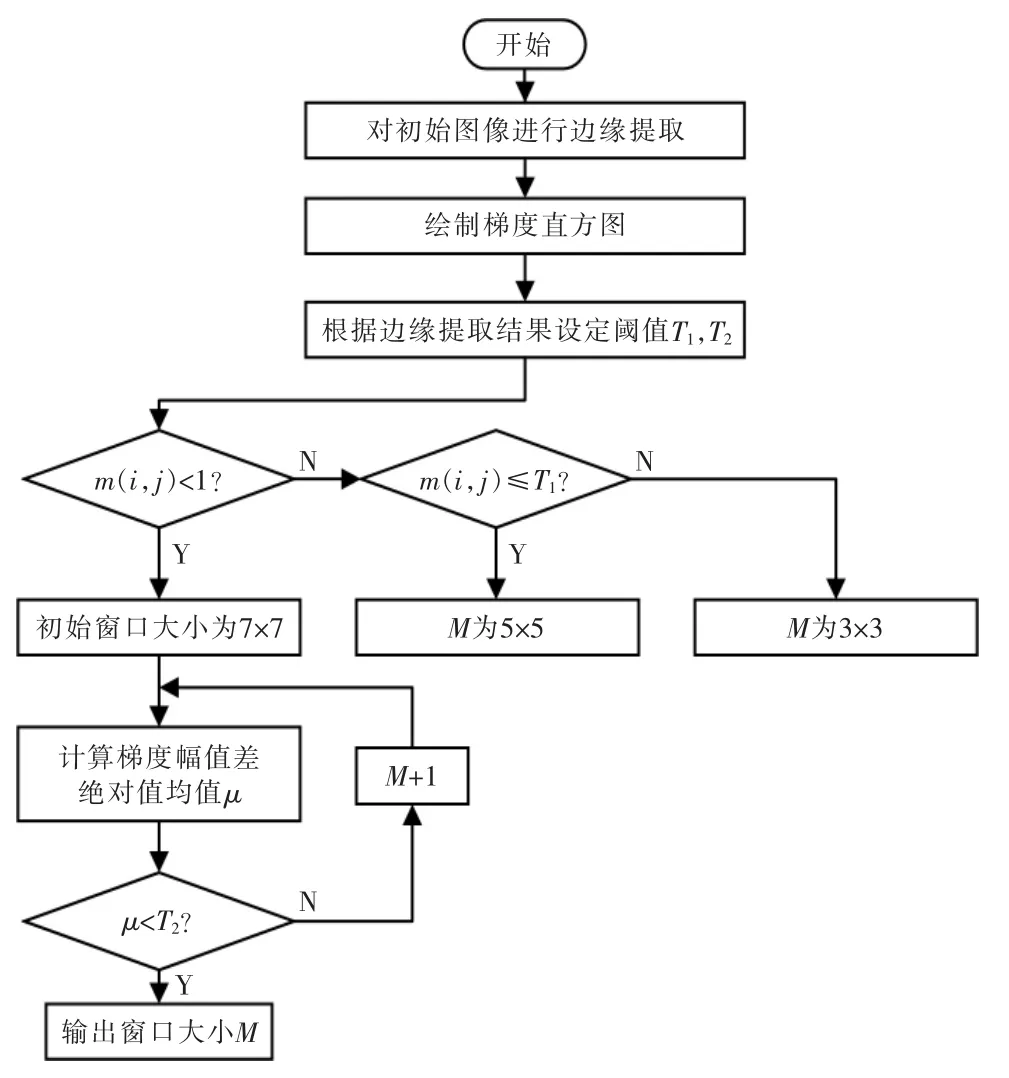
图6 自适应窗口算法流程Fig.6 Flow chart of adaptive window algorithm

在SGM 算法的代价计算环节中加入自适应窗口算法后为SGM_Ada，然后采用Middlebury 中的图像集进行对比实验，现选定最小窗口分别为3×3，5×5。

表1和表2分别是SGM 与SGM_Ada 算法在运行时间及三区域平均误匹配率的对比结果。实验结果表明在含有大量边缘的标准图像中全体区域的误匹配率平均下降了1.21%，而算法运行时间平均增加0.14 s。实验结果表明，SGM_Ada 算法在保持效率的同时提高了全区域平均匹配精度。

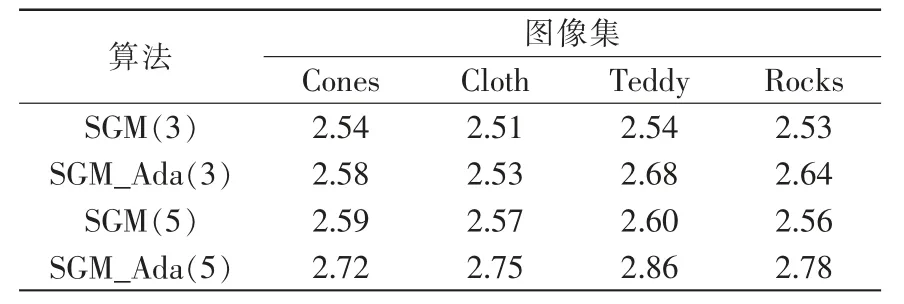
表1 SGM 与SGM_Ada 算法的运行时间对比Tab.1 Comparison of running time between SGM and SGM_Ada algorithm单位：s

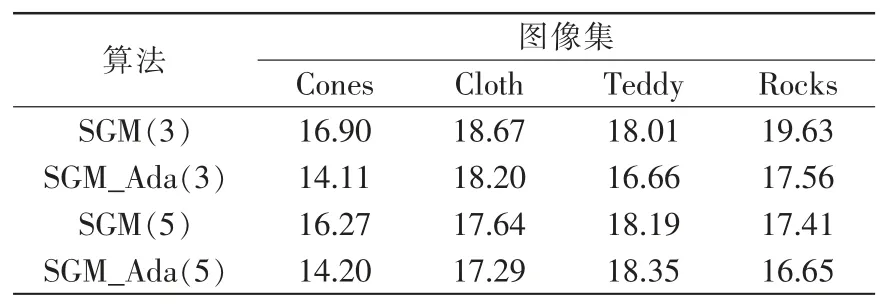
表2 SGM 与SGM_Ada 算法全区域误匹配率对比Tab.2 Comparison of false matching rate（Disc）between SGM and SGM_Ada algorithm/%

3 AD-Census 立体匹配算法及其改进

3.1 AD-Census 立体匹配算法

AD-Census 立体匹配算法原理[14]如图7所示。

图7 AD-Census 立体匹配算法原理图Fig.7 Principle of AD-Census stereo matching algorithm

AD-Census 立体匹配算法中AD 变换基于像素点与待匹配点的灰度值信息，并未考虑周围点的信息；Census 变换窗口固定且未考虑当前点及周围点的梯度信息，匹配效果有限。

3.2 算法改进方案

为提高AD-Census 立体匹配算法的匹配精度，现提出以下改进方案：①AD 变换改为SAD 变换后加入自适应窗口算法，将点对点的搜索模式改为窗口对窗口，该改进步骤加入后算法命名为Ada_1；②在Census 变换中加入融合梯度信息[15]的自适应窗口算法，以上两个改进方案均加入到算法后命名为Ada_2。

3.3 Ada 算法性能测试

表3和表4分别是AD-Census 算法不同窗口大小下的运行时间和误匹配率。

表3 AD-Census 算法的运行时间Tab.3 Running time of AD-Census algorithm单位：s

表4 AD-Census 算法误匹配率Tab.4 False matching rate of AD-Census algorithm/%

由表3和表4可以看出随着窗口增大，运行时间增加且三类区域的误匹配精度均有所下滑，改进前增大窗口对算法表现并无提升作用。

图8为Ada_2 算法在最小窗口为3×3 时不同的阈值T2在Cones 和Rocks 图像测试集中的全区域误匹配率，与表4中窗口大小为3×3 时的数据进行对比，全区域误匹配率分别平均下降了2.06%和2.40%，不同的阈值在一定范围内对算法精度的提升不大。图9为Ada_2 算法在相同条件下不同阈值T2下的运行时间，T2从50 到70 的过程，算法运行时间分别下降了13.54 s 和11.26 s。可得T2取值范围在65～70 时既能提高算法精度，也能保持算法效率。

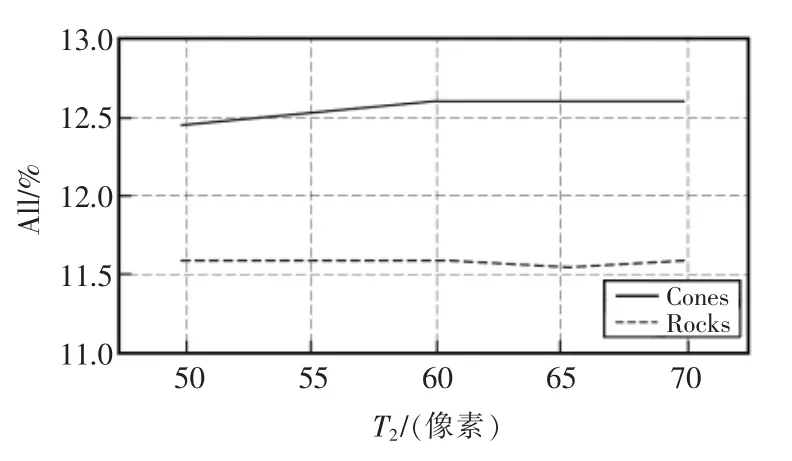
图8 Ada_2 算法误匹配率Fig.8 Mismatch rate of Ada_2 algorithm

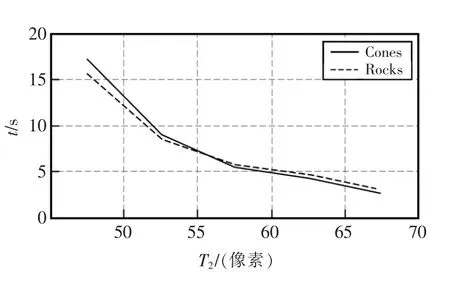
图9 Ada_2 算法运行时间Fig.9 Running time of Ada_2 algorithm

3.4 算法性能对比

为了更清晰地对改进前后的算法的性能进行对比，SGM，AD-Census，Ada_1，Ada_2 在初始窗口为7×7 时的运行时间、误匹配率分别如表5和表6所示。

表5 算法运行时间Tab.5 Running time of different algorithms单位：s

通过表5可得改进后的Ada_2 算法运行时间与改进前的AD-Census 算法相比平均只增加了6.39%。由表6数据，通过比较改进前后的算法在3个区域的误匹配率可以得到在视差非连续区域误匹配率平均下降了7.56%、在全区域误匹配率平均下降了3.21%、在非遮挡区域误匹配率平均下降了1.35%以及三区域平均误匹配率下降了4.05%。Ada_2 算法在Teddy 图像集中视差非连续区域误匹配率下降14.06%。

表6 算法误匹配率Tab.6 False matching rate of different algorithm/%

综合以上结果，改进后的Ada_2 算法与改进前相比，算法精度随着改进步骤的加入逐步提高，与改进前算法相比，窗口大小根据当前点的梯度信息同步调整，与固定窗口大小的算法相比准确性更高。

4 结语

针对立体匹配部分区域匹配精度低的问题，本文提出了一种融合梯度信息的自适应窗口算法。在图像预处理环节提取图像边缘，并求出边缘梯度幅值，根据边缘点的统计结果和梯度幅值求出分类阈值T1，依据T1在匹配代价环节分配不同的窗口，同时设置阈值T2以适配弱纹理区域适当扩大窗口。实验结果表面，在AD-Census 算法中加入自适应窗口算法可以提高算法性能，在Middlebury 的4 个场景中均能在保持算法效率的同时降低算法误匹配率。