基于改进QPSO-SVM的输电线路覆冰厚度预测

乔 鹏，田俊梅

（山西大学 电力与建筑学院，太原 030013）

输电线路覆冰会引起闪络、舞动、断线、倒塔等事故，威胁电力系统的安全稳定运行，由于我国地形地貌多样，输电线路多数要通过严寒地区。因此，开展输电线路覆冰厚度预测研究对于减少线路遭受覆冰灾害，提高电力系统稳定性具有重要意义[1-2]。

国内外研究人员针对覆冰预测模型开展了深入研究。覆冰模型主要分为基于覆冰机理的数学物理模型，如Makkonen 模型[3]和蒋兴良的雾凇覆冰模型[4]等，此类方法在预测精度上较高，但某些参数在实际观测中不易测量[5]。另一类是基于实际历史数据的统计模型，如BP 神经网络[6-8]、支持向量机回归模型[9-10]及其优化算法[11-12]等，但人工神经网络对样本需求量大，易陷入局部最优解，支持向量机适用于小样本且泛化能力较强，得到许多学者的重视。文献[13]采用粒子群算法优化SVM 参数，并预测覆冰厚度，但模型误差较高，预测精度不足。上述模型虽然能较准确地预测线路的覆冰厚度，但都没有考虑各影响因素的权重，不能准确地预测覆冰现象。

因此，本文在已有统计回归模型基础上，提出一种基于历史统计数据的输电线路覆冰厚度预测模型，将差分进化算子和加权系数引入到QPSO-SVM优化算法中，通过改进局部吸引点Sid（t）和粒子个体位置最优的平均值mbest（t），使IQPSO-SVM 算法避免陷入局部最优，导致预测精度降低。同时，利用灰色关联法分析环境因素对覆冰厚度的影响，进一步提取强相关影响因素，并利用IQPSO-SVM 算法对覆冰数据进行拟合，通过算例分析与其他预测模型进行对比来验证算法有效性。

1 算法介绍

1.1 支持向量机（SVM）算法

支持向量机（SVM）是一种基于统计学原理的机器学习算法，把低维空间的线性样本通过非线性映射转化到高维空间来构造回归函数。并将最优化问题转化为凸优化问题。

假定样本容量为｛xi，yi｝（i=1，2，…，m），其中xi表示第i 个样本输入向量，yi是目标函数第i 个样本输出结果，利用非线性函数φ 得到回归方程为

式中：w 表示权值向量；b 表示偏差。

根据结构风险最小化原则，可得SVM 优化问题的目标函数如式（2）所示：

约束条件为

式中：C 为惩罚系数；ε 为误差；ξi与ξi′为松弛变量。

引入拉格朗日乘子和核函数K（x，xi），则式（1）的回归方程最终表示为

惩罚系数C 和核参数σ 对SVM 回归拟合效果影响很大。为了使拟合效果更准确，需要寻找C 和σ 最优解。

1.2 量子粒子群算法

量子粒子群算法（QPSO）是在PSO 的基础上改进的具有量子行为的粒子群算法，利用波函数求解粒子在量子空间的位置与速度，通过求解薛定谔方程得到粒子在空间中某位置的概率密度函数，并用蒙特卡罗随机模拟法得到粒子位置方程。

QPSO 算法是由M 个粒子在D 维空间组成的群体X=｛X1，X2，…，XM｝，t 时刻第i 个粒子的位置为

分析粒子轨迹，若粒子收敛到它的局部吸引点Sid（t），则优化算法收敛，其中Sid（t）表达式如式（6）所示：

式中：c 和r 为（0，1）之间的随机数；Pi表示粒子个体最优位置；Pg表示粒子在全局最优位置，得到粒子的位置更新方程为

式中：u 为（0，1）之间的随机数；α 是创新参数，一般不大于1。

mbest（t）表示粒子最优位置的平均值，如式（9）所示：

标准QPSO 算法原理简单、容易实现，但存在后期寻优过程中易陷入局部最优和粒子收敛不够精准稳定等问题，因此有必要对其改进。

1.3 改进量子粒子群算法

由式（7）可知，粒子的位置更新受到局部吸引点Sid（t）粒子平均最优位置mbest（t）的影响，为了增强粒子在量子空间中的全局搜索能力和提高粒子进准收敛稳定性，本文将分别对这两个变量进行改进。

1.3.1 引入差分进化算子改进Sid

针对粒子群算法中的局部吸引点Sid这种以粒子运动轨迹为指导的计算方式，在算法进行迭代时粒子i 的局部吸引点Sid所处空间逐渐变得狭小，若此时全局最优Pg陷入局部最优位置Pi，会导致粒子群的多样性下降速度较快从而使得QPSO 算法[14]过早地收敛。

首先，从粒子群中随机地选择两个不同粒子a和b，且满足i≠a≠b，则两个粒子间的位置差分公式为

其次，用公式（10）代替公式（7）中的Sid（t），得到新的进化方程如下：

从式（11）中可以看出，位置差分δid（t）避免了群体在由Pi和Pg形成的较小空间内运行而陷入局部最优。

1.3.2 引入加权系数改进mbest（t）

通过式（9）可知标准QPSO 算法mbest（t）的每个粒子都是均等的，但事实上每个粒子对于整体发展都起着不同的作用。因此，根据粒子的适应度数值排序，并分配权重系数β，引入了加权系数的计算公式如式（12）所示：

得到最终的进化方程为

从式（13）中可以看出引入β 可以较好保证粒子运行时靠近最优解，有利于在提高全局搜索能力的同时实现精确收敛，根据式（14）与式（15）更新粒子位置：

2 改进QPSO-SVM 覆冰厚度预测模型

2.1 数据预处理

（1）去除异常数据

依据输电线路形成覆冰的条件去除实测数据中的异常数据。

（2）线性插值

对于缺失数据，利用线性插值使数据具有更好的连续性与平滑性，保证预测结果的准确性。

（3）数据归一化

由于影响输电线路覆冰厚度的因素众多，且各因素数据的单位量纲不同，为避免不同数据集的值相距较大，因此需要统一量纲，归一化处理如式（16）所示：

式中：xi表示原始值；xmin和xmax分别表示最小值和最大值；xi′表示归一化后的值。

2.2 模型构建步骤

改进QPSO-SVM 流程框图如图1所示，具体建模流程如下：

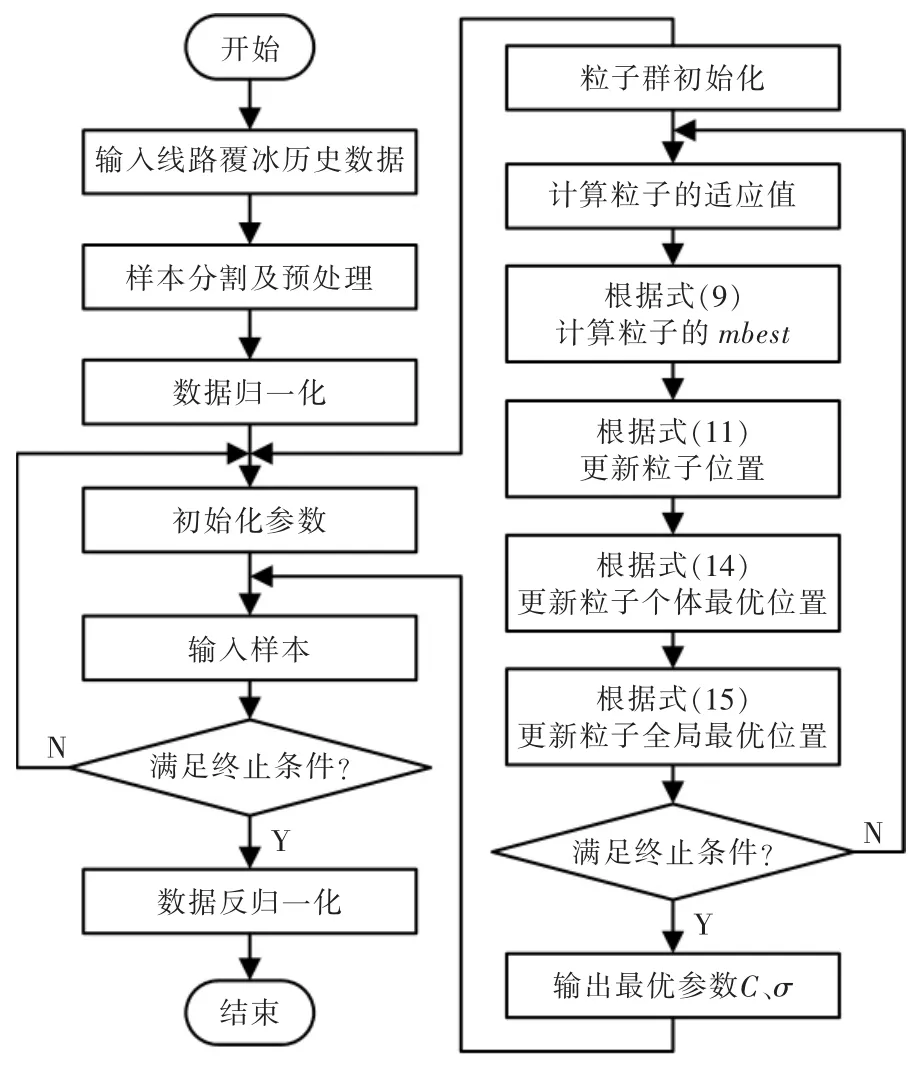
图1 改进QPSO-SVM 算法流程Fig.1 Flow chart of improved QPSO-SVM algorithm

（1）初始化模型参数并计算粒子适应度值；

（2）根据式（12）计算粒子的平均最好位置；

（3）开始执行迭代，根据式（11）更新粒子的位置，得到C 和σ 一组新解；

（4）比较适应度值，并利用式（14）与式（15）更新粒子个体最优位置和粒子全局最优位置；

（5）根据迭代终止条件判断结果是否满足要求。若是，则输出解；否则，返回步骤（4）继续迭代。

2.3 模型评价指标

采用平均绝对误差百分比（mean absolute-percentage error，MAPE）和均方根误差（root mean square error，RMSE）的模型预期影响指数，来检验模型估计结论的正确性。

（1）平均绝对误差百分比（MAPE）

（2）均方根误差（RMSE）

3 仿真算例分析

3.1 数据选取及灰色关联度分析

线路覆冰现实情况比较复杂，如果根据实际情况选择输入变量，则预测模型影响因素较多，使模型效率下降，学习时间变长；若过于简化输入量的个数，则导致模型预测准确性降低等问题。因此，采用灰色关联分析法[15]，找出影响导线覆冰厚度的关键因素，结合云南地区某500 kV 架空输电线路覆冰监测数据进行算例分析。线路等值覆冰厚度数据来源于监测装置，温度、湿度、风速、气压等数据来源于当地气象部门，如图2和图3所示。

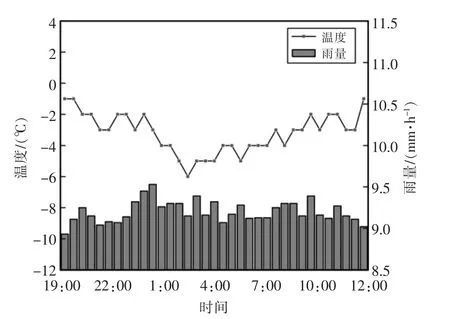
图2 环境温度和雨量历史数据Fig.2 Historical data of ambient temperature and rainfall

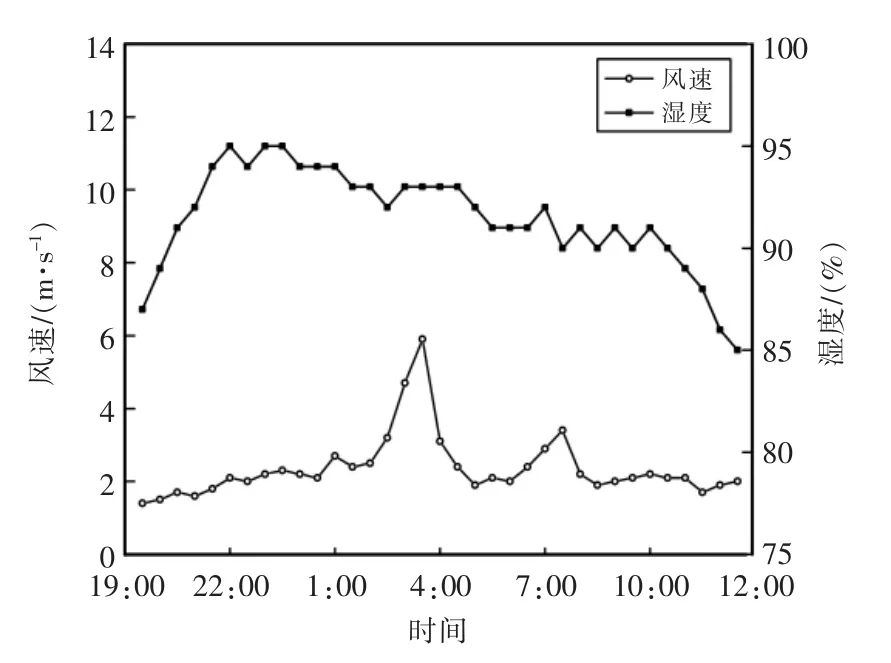
图3 环境风速和湿度历史数据Fig.3 Historical data of ambient wind speed and humidity

本次覆冰增长时间为实验记录中的第1 天晚上19：00 至第2 天早上12：00； 数据采集间隔时间为30 min，共获得35 组数据。部分数据如表1所示。

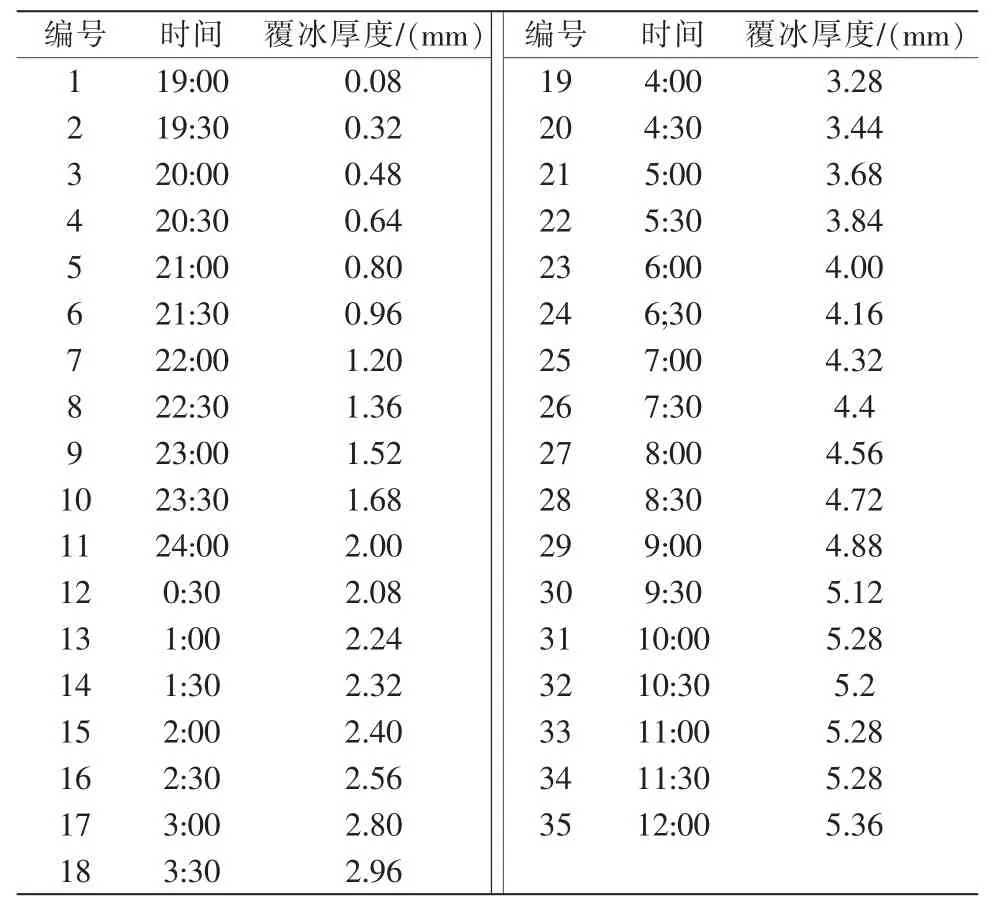
表1 部分覆冰历史数据Tab.1 Partial icing historical data

利用Python 计算分析，得到线路覆冰厚度与其他影响因素之间的相关性如表2所示。

表2 各影响因素与覆冰厚度的灰色关联度Tab.2 Grey correlation degree between each influencing factor and ice thickness

关联度小于0.5 为弱相关性，0.5～1 呈强相关性。由表2可知，相关性强弱顺序为：温度＞风速＞雨量＞湿度＞气压；其中，环境温度关联度最高，说明温度与覆冰预测呈强相关，气压排在最后，关联度小于0.5，属于弱相关。

3.2 预测模型验证分析

选取强相关因素，将温度、湿度、风速、雨量作为输入变量，覆冰厚度作为输出量。通过与经典的SVM，PSO-SVM，QPSO-SVM 算法对比分析验证模型有效性。

表1中部分历史数据中编号1～25 设为训练集，编号26～35 设为测试集。设定SVM 初始值C=100，δ=1，利用改进算法对参数寻优后，得到参数为c=50.24，δ=28.08。其他参数设定：种群数N＝200，最大迭代次数kmax=100，粒子维度D=3，粒子位置最大值为60，粒子位置最小值为0.001，alpha 从1～0.4 线性降低，beta 从1.5～0.5 线性降低。四种模型误差预测对比如图4和表3所示。

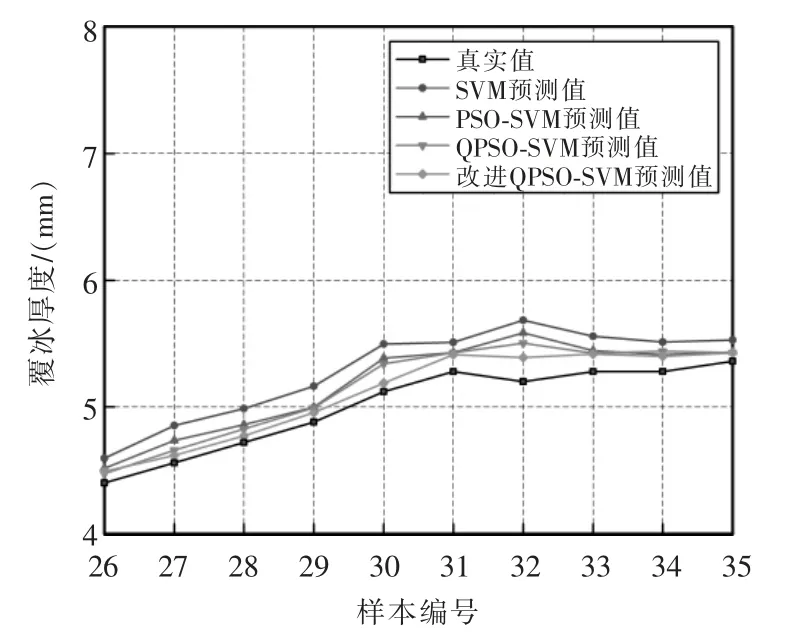
图4 四种预测模型预测结果对比Fig.4 Comparison of prediction results of four prediction models

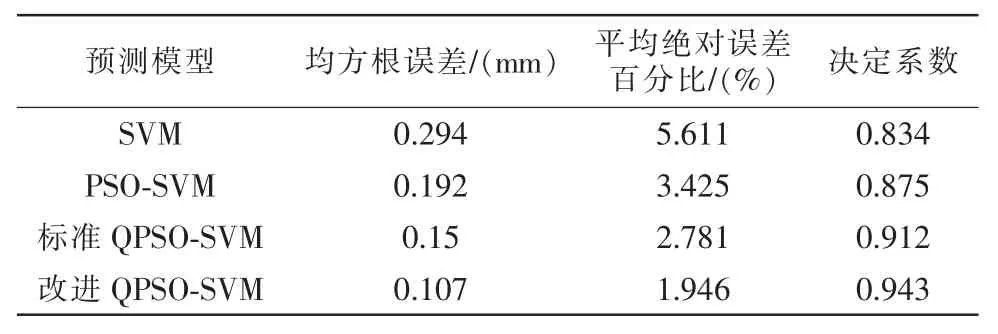
表3 四种模型误差预测对比Tab.3 Comparison of error prediction of four models

由表3对比可知，改进OPSO-SVM 覆冰厚度预测模型的各项评价指标都更优，与经典预测模型相比，改进QPSO-SVM 模型的平均绝对误差百分比相较前者分别下降了65.3%、43.2%、30%；均方根误差相较标准QPSO-SVM 下降至0.107 m；决定系数趋近1，说明模型拟合效果准确，且改进QPSO-SVM 决定系数最高。这表明模型的预测结果较为符合实际覆冰情况，更加适合覆冰厚度预测。

QPSO-SVM 与IQPSO-SVM 训练过程中的拟合曲线如图5所示。

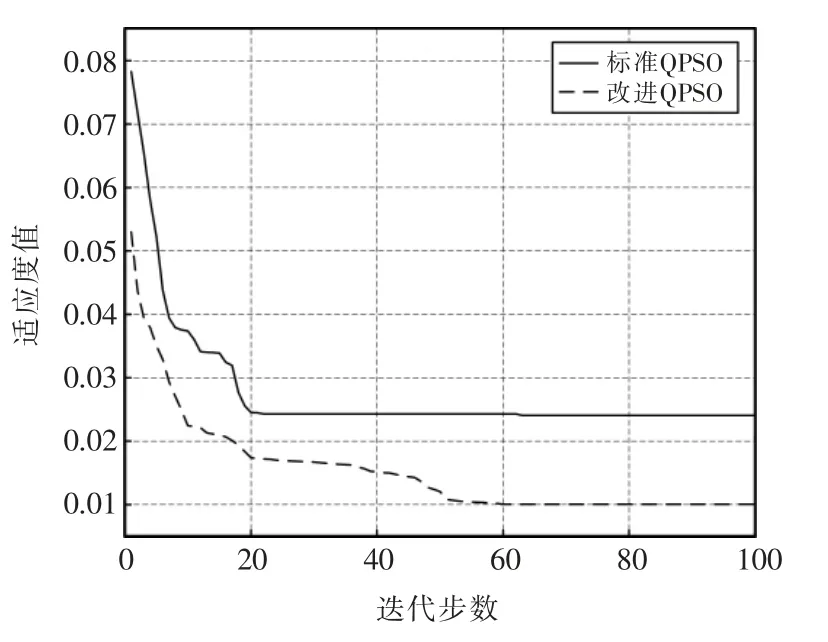
图5 两种算法迭代图Fig.5 Iterative diagram of two algorithms

由图5可知，相对于标准QPSO 算法而言，改进QPSO-SVM 模型算法在0～20 代阶段波动性较强，表现出本文的改进算法在寻优前期具有快速精确的收敛能力；在算法中后期，标准QPSO 算法在21 代和63 代都达到了一个较为平衡的数值，所以可以认为标准QPSO 算法在21 代时趋于稳定，并寻到了全局最优解。但本文IQPSO-SVM 算法，分别在36 代、51 代两次跳出局部最优解，并持续不断地寻找全局最优解，直到第60 代才趋于稳定，但也存在预测时间较长等缺点。结果分析表明，改进QPSO算法相比于标准QPSO 算法，在优化多维函数时粒子寻优方向更明确，提高了计算精度和全局收敛性。

4 结语

本文考虑环境因素对线路覆冰厚度影响，采用灰色关联法选取强相关因素作为输入变量，提出一种IQPSO-SVM 覆冰厚度预测模型，通过算例分析得到如下结论：IQPSO-SVM 与其他模型相比在处理小样本数据时预测精度更高，收敛性更好。克服了后期寻优过程中易陷入局部最优和粒子收敛不够精准稳定等问题，具有一定的应用价值。