具有饱和效应的任意阶自催化反应扩散模型的Turing不稳定性和Hopf分支
郭改慧, 郭飞燕, 李纪纯
(陕西科技大学 数学与数据科学学院, 西安 710021)
0 引 言
Turing不稳定性是指扩散可能破坏反应扩散系统的稳态平衡, 并导致非均匀的空间模式[1].为验证该结论, 关于化学和生物背景下反应扩散模型的Turing不稳定性研究得到广泛关注.如Lengyel-Epstein反应扩散模型[2-3]和自催化化学反应的Brusselator模型[4-5]等.当反应速率相同且反应物初始浓度不变时, 任意阶自催化模型可表示为

(1)
其中:Ω⊂N(N≥1)为具有光滑边界∂Ω的有界开集,υ表示∂Ω上的单位外法向量;u,v分别表示反应物和催化剂的无量纲浓度, 通常认为是非负的;d1,d2分别表示反应物和催化剂的扩散系数, 均为正常数;Δ为Laplace算子;a,p均为正常数.
对于系统(1), 文献[6]以a为分支参数证明了Hopf分支和稳态分岔的存在性, 同时得到了由扩散引起的Turing不稳定性;文献[7]补充了文献[6]的结果, 进一步建立了由扩散系数引起的Turing不稳定区域, 同时讨论了扩散系数对Hopf分支存在性的影响; 文献[8]讨论了其唯一正常数平衡点稳态分岔的稳定性;文献[9]证明了当p=2时其非常数稳态解的存在性和不存在性, 并讨论了高维情形下其唯一正常数平衡点所产生的局部稳态分岔.
饱和效应是指反应物与生成物之间的饱和程度.由于生物和化学反应过程通常会受饱和效应的影响, 因此研究模型在饱和效应下的动力学行为非常必要.文献[10]讨论了具有饱和效应的Sel’kov模型正平衡点的稳定性及非常数稳态解的存在性和不存在性;文献[11]研究了具有饱和效应的Sel’kov模型周期解的Turing不稳定性.本文在系统(1)的基础上考虑一类具有饱和效应的任意阶自催化反应扩散模型:

(2)
其中k为饱和系数.本文主要研究系统(2)正平衡点的稳定性、Hopf分支存在性以及由扩散引起的Turing不稳定性.显然, 系统(2)存在唯一的正平衡点(u*,v*)=(a1-p+ka,a).
1 常微分系统的稳定性和Hopf分支
下面针对系统(2)相应的常微分系统

(3)
给出其正平衡点(u*,v*)的稳定性和Hopf分支的存在性及稳定性.
系统(3)在(u*,v*)处的Jacobi矩阵为
设其特征方程为λ2-Tλ+G=0, 其中


1) 若a>a0, 则系统(3)的唯一正平衡点(u*,v*)局部渐近稳定;
2) 若a 3) 若a=a0, 则系统(3)在正平衡点(u*,v*)处产生Hopf分支, 且当kp<1时, 该Hopf分支方向为次临界的, 分支周期解渐近稳定; 当kp>1时, 该Hopf分支为超临界的, 分支周期解不稳定. 证明: 当a>a0时,T<0且G>0, 此时Jacobi矩阵J的特征值均具有负实部, 故正平衡点(u*,v*)局部渐近稳定; 当a 当a=a0时,J存在一对纯虚根.设λ=α(a)±iβ(a)为J在a=a0附近的一对共轭复根, 其中 计算可得 (4) 方程组(4)可改写为 (5) 其中F2(u,v,a)=-F1(u,v,a), 且 这里 显然, 当a=a0时, 有 其中 下面通过计算d(a0)的符号给出Hopf分支方向以及周期解的稳定性[12], 其中 (6) (7) 将式(7)代入式(6), 并整理得 由于α′(a0)<0, 因此根据Poincare-Andronov-Hopf分支定理[12]可知, 系统(3)在正平衡点(u*,v*)处产生Hopf分支.当kp<1时, 该Hopf分支方向是次临界的, 且分支周期解渐近稳定; 当kp>1时, 该Hopf分支方向为超临界的, 且分支周期解不稳定. 下面在一维空间Ω=(0,π)上讨论正平衡点(u*,v*)对系统(2)的稳定性, 给出系统(2)的Turing不稳定性及Hopf分支的存在性. 定义实Sobolev空间X={(u,v)∈H2(0,π)×H2(0,π): (ux,vx)|x=0,π=0},X的复延拓空间XC=X⊕iX={x1+ix2|x1,x2∈X}.算子-Δ在齐次Neumann边界条件下的特征值为μn=n2(n∈0={0,1,2,…}), 且φn=cos(nx)(n∈0)为对应μn的特征函数.系统(2)在平衡点处的线性化算子为 L的所有特征值均可由Ln的特征值给出, 其中 设Ln的特征方程为μ2-Tnμ+Dn=0,n∈0, 其中 注意到二次函数 h(z)=a2pz2-2ap(p+1+kap)z+(1-p+kap)2 的判别式 因此h(z)=0存在两个实根: 定理2设p>1.当a 下面讨论a0 存在两个正实根: (8) 其中 R=d2A+d1N=-(1-p+kap)d1-apd2,D=ap(1+kap)>0. 令 易知当0 关于d1求导, 可得 定义 Φ1={μ|μ≥0,μ-(d1,d2)<μ<μ+(d1,d2)},Φ2={μ0,μ1,μ2,…}. 下面讨论由扩散引起的Turing不稳定性.若使0 对于任意的d1>0, 有0<μ+(d1,d2)<μ*.如果μ1>μ*, 则Φ1∩Φ2=Ø, 即对所有的n∈,Dn>0且Tn<0, 故系统(2)的正平衡点(u*,v*)局部渐近稳定.从而可得: 证明: 固定d1, 令d2→0, 则 定理5设p>1, 且d1,d2满足 (9) 则当a=a0时, 系统(2)在(u*,v*)处产生空间齐次的Hopf分支. 证明: 当a=a0时,T0=0且D0>0.因为μn>0(n≥1)且d1,d2>0, 故对于任意的n≥1, 均有Tn(a0)<0.经计算, 当d1,d2满足式(9)时, 对任意的n≥1, 均有Dn(a0)>0.因此, 当a=a0时, 算子L除一对共轭纯虚根外, 其他特征值均具有负实部.令μ=δ1(a)±iδ2(a)为算子L在a=a0附近的一对共轭复根, 则 由Hopf分支定理[12]知, 当a=a0时系统(2)在(u*,v*)处产生空间齐次的Hopf分支. 对于常微分系统(3), 取p=2,k=15/49, 则a0=0.875.若取a=1>a0, 则由定理1知, 其正平衡点(u*,v*)局部渐近稳定, 如图1所示.若取a=0.87 图1 当参数a=1时系统(3)正平衡点局部渐近稳定Fig.1 Positive equilibrium point of system (3) is locally asymptotically stable when parameter a=1 对于偏微分系统(2), 取Ω=(0,π), 当p=3,k=0.1时,a0=1.220 5,a*=2.714 4.若取a=2, 则z1=0.019 1.当d1=4,d2=7时, 满足d2>d1z1, 由定理2知系统(2)的正平衡点(u*,v*)局部渐近稳定, 如图3所示.当d1=1,d2=0.005时, 满足0 图2 当参数a=0.87时系统(3)产生稳定周期闭轨Fig.2 System (3) produces stable periodic closed orbit when parameter a=0.87 图3 当参数d1=4, d2=7时系统(2)的正平衡点局部渐近稳定Fig.3 Positive equilibrium point of system (2) is locally asymptotically stable when parameters d1=4, d2=7 图4 当参数d1=1, d2=0.005时系统(2)产生非常数稳态分支Fig.4 System (2) produces nonconstant steady-state bifurcation when parameters d1=1, d2=0.005 图5 当参数d1=4, d2=7时系统(2)产生稳定的分支周期解Fig.5 System (2) produces stable bifurcation periodic solution when parameters d1=4, d2=7 综上所述, 本文在Neumann边界条件下研究了一类具有饱和效应的任意阶自催化反应扩散模型.以a为分支参数, 分别给出了常微分系统和扩散系统平衡点的稳定性和Hopf分支的存在性.特别对于扩散系统, 给出了扩散系数对平衡点稳定性的影响.结果表明: 当a较小时, 正平衡点不稳定; 当a较大时, 正平衡点稳定; 当a介于某一范围内时, 扩散系数的比值d2/d1将影响平衡点的稳定性.当d2/d1适当大时, 平衡点仍然是稳定的; 当d2/d1适当小时, 平衡点可能稳定, 也可能出现Turing不稳定现象; 当d2/d1满足一定条件时, 系统会产生空间齐次的Hopf分支.
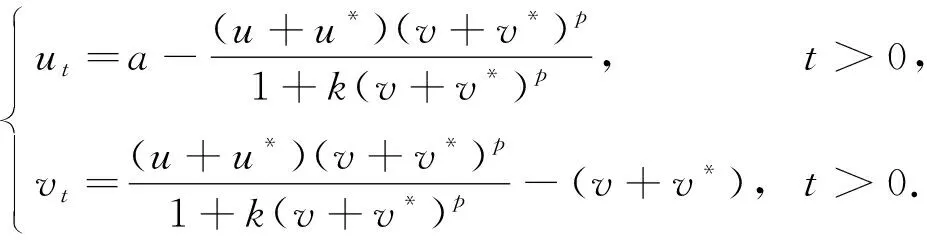
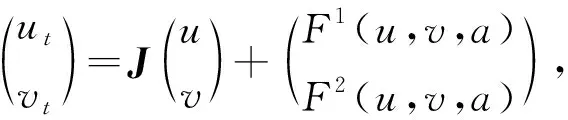
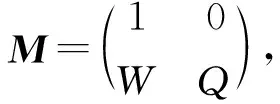


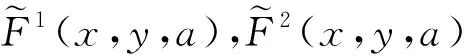

2 扩散系统的Turing不稳定性和Hopf分支



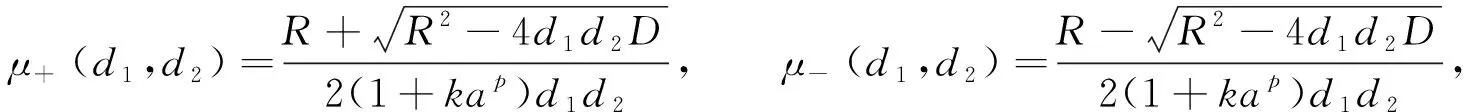
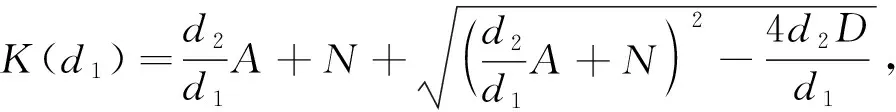





3 数值模拟