有理参数曲线的C1分段根式弧角重新参数化算法研究

顾 特

（广西民族大学 人工智能学院，广西 南宁 530006）

0 引言

曲线曲面的参数表示常被应用于计算机图形学与计算机辅助几何设计领域，其优点为表达方便、易于显示。对于参数曲线而言，有些参数具有几何意义，主要包括弧长参数、弦长参数和弧角参数等。其中，曲线的弧长参数能够均匀划分曲线的长度，在实际生活中有广泛应用［1-4］；弧角参数则能更好地反映曲线在各个位置上曲率的变化。尽管所体现的性质有所不同，但是在研究弧长和弧角参数的过程中所采用的思想有很多相似之处。在几何设计和造型中，有理参数表示具有简单、直观、易于实现的优点，因此研究有理弧长参数和有理弧角参数具有重要意义。

关于有理弧长参数，Gil 等［5］证明了任意平面曲线都具有弧长参数，但是这些参数表达式不一定是有理的；Farouki 等［6］证明了在平面曲线中，只有直线具有有理弧长参数化；Salkkalis 等［7］证明了在Rn空间中，仅有直线具有有理弧长参数。因此，求得一般曲线的有理弧长参数表示几乎是不可能的。于是研究者们转而寻找一般曲线的有理近似弧长参数。例如，Farouki［8］提出一种当次数不变的情况下，基于Möbius 参数变换计算B 线条的最优参数化方法；Costantini 等［9］提出用一种分段的Möbius 变换近似弧长参数化变换，并且证明了分段区间越小分段越多，得到的参数变换越接近于弧长参数变换；Liang 等［10］提出一种C1连续的分段有理在参数化算法，该算法是基于实验结果实现的。

关于有理弧角参数，最早由Patterson 等［11］提出一种曲率参数，该参数是由参数曲线的弧长参数和曲率公式推导得到的。利用曲率参数作图能将更多的点集中在曲率更大的地方，从而反映曲线在各个位置的弯曲程度。与弧长参数表示相似，一般来说曲率参数没有解析表达式，因此对一般曲线无法精确求出其曲率参数表示。为此，Patterson 等给出了一种数值近似曲率参数化的算法，但该算法高度依赖于作图点的数目，如果作图点数目发生改变，则必须重新计算其曲率参数化，因而效率较低。此后，Yang等［12-16］提出一套曲线均匀弧角参数化理论，该理论首先定义了一个角速度均匀度函数，用衡量曲线的某种参数表示接近弧角参数表示的程度，同时指出如果一条参数曲线某一参数表达式的角速度是均匀的（也就是角速度函数等于不为0 的常数），那么随着参数变化曲线的弯曲程度也是均匀的，这也就是标准弧角参数，其与曲率参数在作图时有着相同的特性。同样，弧角参数也难以求得有理的解析表达式。因此，该理论提出了计算曲线有理近似弧角参数表示的多种算法，其主要思想是通过分段的Möbius 变换近似非有理的弧角参数变换。此后，刘振华等［17］根据曲线均匀弧角参数化理论设计出软件包ImUp+，这个软件包可以对原来曲线参数进行优化而得到新的参数，利用新参数绘制的曲线比原来的曲线更加光滑。

然而，如果给出的参数角速度函数含零点，这些重新参数化的算法无法很好地均匀化零点附近的角速度，这也是为什么ImUp+［17］要求处理的参数角速度函数不含有零点。为了完善曲线均匀弧角参数化理论，优化角速度函数含有零点参数表达式的角速度均匀度，本文针对角速度包含零点的参数曲线，考虑其C1连续的根式近似弧角参数化。通过引入C1连续性的约束计算得到角速度不包含零点的C1连续参数表示，然后使用文献［16］中C1连续的优化弧角重新参数化算法，对已经得到的参数表示进行有理的重新参数化，以得到曲线的近似弧角参数表示。计算实例表明本文方法可以在C1连续性的约束条件下有效解决角速度包含零点的弧角重新参数化问题。

1 研究背景

本章阐述关于角速度均匀的变量用于衡量近似弧角参数接近弧角参数的程度，给出分段Möbius 变换的定义，其将在2.1 节求取曲线角速度函数不含零点的参数以及2.2节优化角速度均匀度时被用到。

对平面曲线的某一参数表示为：

其角速度函数为：

定义其角速度均匀度为［15］：

设t=r(s)为［0，1］上的单调变换，将p与r 复合可以得到原曲线的一个新的参数表示p°r，该过程称为重新参数化，可以证明重新参数化后的角速度函数为［15］：

则称如上定义的m为分段Möbius 变换。需要注意的是，任一分段Möbius 变换m均可由一组参数序列T、S、α表示。

2 理论基础

若参数曲线角速度函数含有零点，则基于文献［12-16］的算法均会失效。为解决这一问题，2.1 节给出将角速度函数含有零点的参数重新参数化为不含有零点参数的算法。新的参数角速度函数并非C1连续，为了使用文献［16］中的算法对2.1 节的结果进行优化得到近似弧角参数，在2.2 节对文献［16］中的算法进行了改进，最后在2.3节给出了化简所得近似弧角参数表达式的方法。

2.1 用C1根式变换为角速度函数去零点

当ωp(t0)=0 时，如果通过变换φ(z)调整t0附近角速度的均匀度，那么φ(z)应当满足：

其中，z0=φ-1(t0)，a>0。式（10）是一个微分方程，通过求解该方程，即可得到想要的变换φ(z)。另一方面，参数表示的角速度函数可能有多个零点，而式（10）所得到的结果只针对其中某个零点，为了能够处理每一个零点，考虑φ(z)为分段变换。

通过调整式（10）解的形式，可以使得φ＇(z) 在[ti-δ，ti+δ]上保持连续，从而ωp°φ(z)在[ti-δ，ti+δ]上连续，但是φ＇(z)在区间端点ti-δ和ti+δ由于左右极限不连续，ωp°φ(z)将出现跳跃间断点。为了使得变换后角速度函数在[0，1]上连续，再对z做分段Möbius 变换mc，使得变换后ωp°φ°mc(s)在[0，1]连续。

定理1设p为曲线的一个参数表示，p的角速度函数在(0，1)仅有N个零点t1，...，ti，...，tN，λi为零点ti的重数，那么参数表达式p°φ°mc的角速度函数在(0，1)上连续且不含零点，其中φ为分段根式变换，表示为：

此 处，0 <δ<1 且ti∉[ti-1-δ，ti-1+δ]；mc为分段Möbius变换，表示为：

定理1 并没有考虑ti=0 或ti=1 的情况，这是由于ti∈(0，1)时，φi(z)是对ti两侧进行变换，ti=0 或1 的特殊情况只需要对半边做变换即可，因此不再给出这两种简单情况的参数变换表达式。

首先证 明参数表示p°φ的角速 度函数ωp°φ(z)在(0，1)上不含零点。

由 式（16）可 知φ＇(z) >0，而ωp°φ(z)=ωp(φ(z)) ⋅φ＇(z)，当t≠ti，ωp(t) ≠0，因此对除zi=φ-1(ti)以外的点，ωp°φ(z) >0。现在考 虑zi=φ-1(ti) 的情况，当t∈[ti-δ，ti+δ]时，ωp(t)可以表示为：

综上可知，ωp°φ(z)在(0，1)上不含零点。

故ωp°φ°mc在端点ti-δ处连续，同理可证ωp°φ°mc在端点ti+δ处也连续，因此ωp°φ°mc在(0，1)上没有零点且连续。

利用定理1 中的变换对于角速度函数含有零点的参数表示重新参数化后，可以得到角速度函数不含零点且连续的参数表示，这一过程称为去零点。

2.2 重新参数化后的角速度均匀度优化

2.1 节中去零点的过程并未对参数表示的角速度均匀度进行优化，以下将改进文献［16］中的变换，对定理1 中得到的参数表示p*=p°φ°mc进行重新参数化，继续对角速度均匀度进行优化，从而得到原参数曲线的近似弧角参数化。

定理2［16］若p为曲线的参数表达式，ωp在［0，1］上C1连续，mo是由序列S，R，α确定的分段Möbius 变换，其中S、R表示为：

其中，M-1 为(s)零点个数，而α通过以下公式得到：

定理2 要求ωp在［0，1］上C1连续，而ωp*仅在分段内满足C1连续的条件，在分段点ti-δ和ti+δ处则为C0连续。若要使用定理2 对p*进行优化的重新参数化，则需对连续条件进行弱化。定理2 中选取分段点的目的是将ωp拆分为单调的分段，虽然ωp*在分段点处不连续，但仍可以根据其左右导数的符号确定是否将该分段点加入S中。即：若，则 将ti-δ并 入S；若成立，则将ti+δ并入S。在定理2 中式（21）用于确认分段点，保证分段点内部角速度函数单调性一致，式（22）是求得基于式（21）的分段Möbius 变换最优的α。在保证分段内角速度函数单调性一致的条件下，分段数越多，定理2 给出的分段Möbius 变换能更好地近似弧角参数变换。文献［16］还给出了一种加细划分的算法，对式（21）给出的分段做进一步划分，这种划分方式是基于式（23）对分段[si-1，si]进行求解：

将得到的新解并入S得到新的分段S1，令S=S1，重复定理2 的过程就能得到分段数更多的分段Möbius 变换，反复执行这一过程就能得到近似弧角参数变换m*。由于ωp*＇在分段点处不连续，若要使用式（23）进行加细划分，也需要对连续条件进行弱化，令：

2.3 基于分段根式变换的近似弧角参数变换

m* 可 与mc复合为 一分段Möbius 变 换mf，即mf=mc°m*。最后得到φ*=φ °mf，即为C1连续的近似弧角参数变换。

定理3设m1为分段Möbius 变换，其参数序列为T1，S1，α1；m2为相容的分段Möbius 变换，其参数序列为S2，R2，α2，变换m3=m1°m2，那么m3也是分段Möbius 变换且由T3，R3，α3确定，其中：

当 [t3k-1，t3k]⊆[t1i-1，t1i]，[r3k-1，r3k]⊆[r2j-1，r2j]时：

又由于：

这里A，-α3kt3k-1-α3kt3k+t3k-1为常数，故：

因此式（26）成立。

3 示例与实验

基于定理1-3，本节给出一个平面曲线的弧角重新参数化算法，用于对角速度包含零点的平面有理参数曲线进行C1分段近似弧角重新参数化。算法1 为主算法，设计思路包括两部分，第一步是将角速度包含零点的平面有理参数曲线重新参数化，使得新参数表示的角速度函数不再包含零点且角速度函数保持C1连续性；第二步是对新参数表示计算C1连续的有理分段近似弧角参数变换（即算法2）。

3.1 算法

算法1为C1分段近似弧角重新参数化算法：Arc_angle_reparam（p，δ）

算法2为角速度均匀度优化算法：Optimize（ωp*，S，Z，n）

3.2 示例

1.计算p的角速度函数为：

2.计算ωp的零点集及零点的重数U=[ 1 ]。

3.计算p的角速度均值及角速度均匀度为：

4.对p做分段变换φ(z)，令δ=0.1，对做变换φ1(z)，其他区域做恒等变换得到：

5.对p°φ做分段Möbius 变换mc使得ωp°φ°mc连续，计算得参数序列为：

6.复合p°φ和mc并计算ωp°φ°mc得：

7.计算ωp°φ°mc的极值点为s=0.6，得到第一次优化变换前后的参数序列为：

再由式（21）计算得到α*=[0.767，0.182]。

8.由式（23）和S*，R*，α*计算得到对S*新的分割Snew，令S*=Snew再计算R*和α*，重复2 次以后得到一个新的加细划分S*及对应的R*和α*：

9.设m*为由S*，R*，α*构造的Möbius 变换，则m*即为参数表示p° φ °mc的近似弧角参数变换。

10.利用式（26）对m*，mc复合得到mf，再对φ 和mf复合得到φ °mf，此即为曲线p的近似弧角参数变换：

此时计算p°φ°mf的角速度均匀度为：

图1 左右图分别为原参数表示的角速度函数ωp(t)和再参数化后角速度函数ωp°φ°mf(s)对比μp的函数图像。

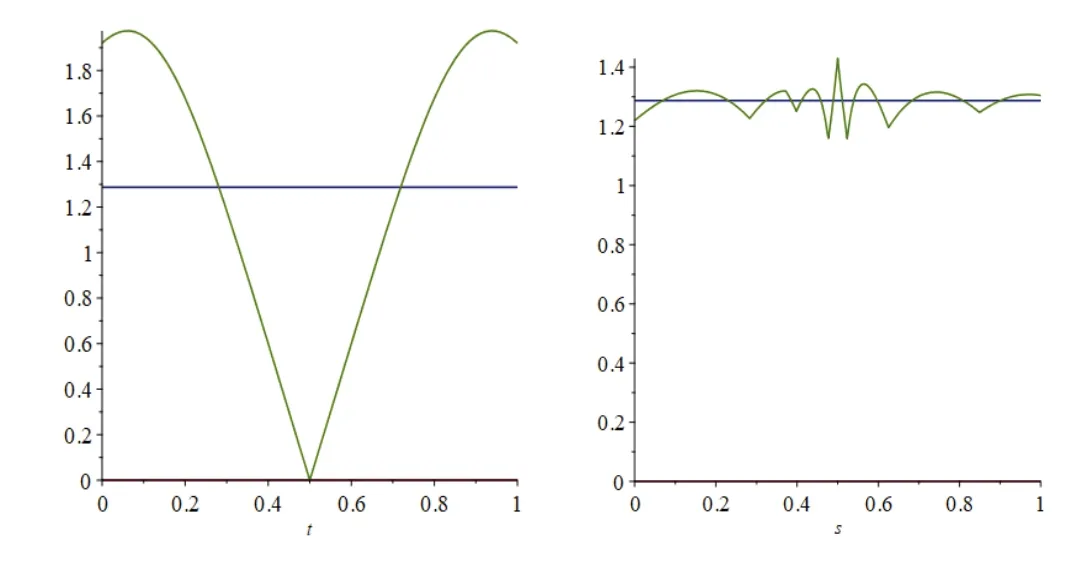
Fig.1 Angular velocity functions for parameters t and s图1 参数t和s的角速度函数

p的弧角参数变换为：

图2 左图为p的弧角参数变换函数v(s)，右图为p的近似弧角参数变换函数φ°mf(s)。

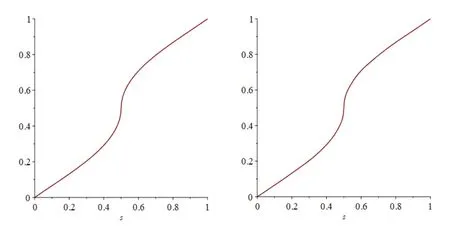
Fig.2 Approximate arc-angle parameter transformation and arc-angle parameter transformation图2 近似弧角参数变换和弧角参数变换

图3 左图为利用参数表达p(t)对t均匀取点后作图的效果，右图为利用p°φ°mf(s)参数表达对s 均匀取点后作图的效果。

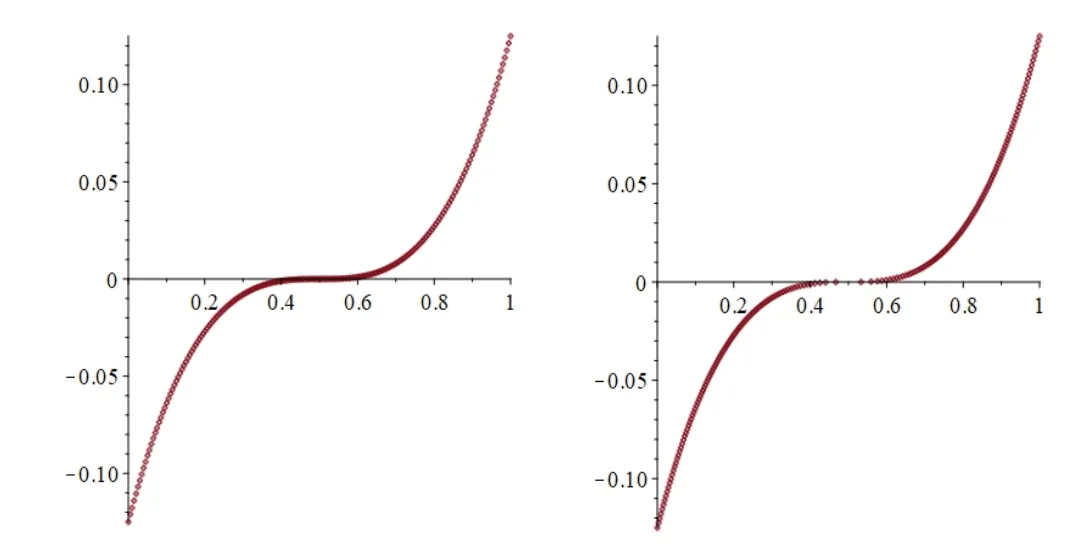
Fig.3 Images of example curve generated by parameter t and s图3 示例曲线关于参数t和参数s生成的图像

3.3 实验结果与分析

本文算法已在Maple 19 上进行了初步实现，并对文献［18］中部分角速度函数有零点的有理参数曲线进行计算，对本文提出的C1分段近似弧角重新参数化算法的有效性进行了验证。实验环境配置如下：PC 处理器为Intel（R）Core（TM）i7-9750H CPU @2.60GHz，内存为8GB RAM。

实验结果如表1 所示，其中up表示曲线的参数表示p的角速度均匀度，up°φ°mf表示对p再参数化后得到的参数表示p°φ°mf的角速度均匀度。

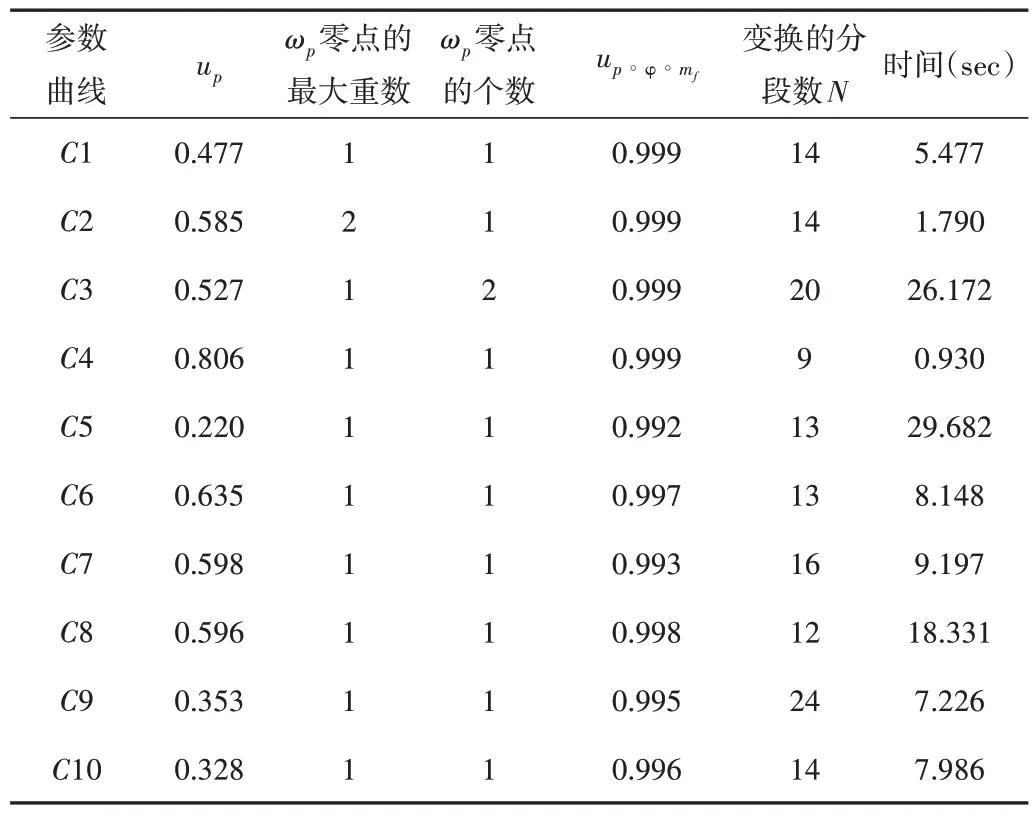
Table 1 Experimental results of radical arc-angle reparameterization表1 根式弧角重新参数化实验结果

对角速度包含零点的参数表示计算其C1近似弧角重新参数化的问题是在本文中首次得到解决的，因而没有可比较的文献。分段数和角速度函数的复杂性决定了本文算法的运算效率。从表1 中可以看出，C1分段根式重新参数化使得角速度均匀度有了显著提高。然而，计算结果中的分段数通常都大于10，这是由于在第一次去除零点的根式变换中做了一次分段，并在后续优化角速度均匀度时又进行了加细分段，每一个零点会增加3 个分段，优化角速度均匀度的过程一般需要迭代3～4 次。而3.2 节中所采用的方法对曲线角速度均匀性的改善有限，这是由于该方法对某些特殊的例子仍存在局限，需要对初始分段点进行一定优化，以得到更好的效果。

4 结语

本文介绍了一种C1分段根式近似弧角重新参数化的算法，在利用参数曲线绘图时，利用这一算法可有效提升带有拐点曲线的光滑度。由于该算法在重新参数化的过程中会大量用到角速度函数的积分，如何简化角速度的形式以提高算法的运行效率是未来需要考虑的一个问题。此外，本文算法思想也适用于一些弧长参数化的应用［19-21］，可以对非正则有理参数曲线计算其C1分段根式近似弧长重新参数化。