基于改进Canny的彩色图像边缘检测算法
安帅帅,李庆忠
(中国海洋大学 工程学院,山东 青岛 266100)
0 引言
图像边缘检测一直是图像处理和计算机视觉领域的研究热点之一,在图像分割、目标检测与识别等领域有着广泛应用[1-3]。目前,已有大量关于灰度图像的边缘检测方法,但对于普遍使用的彩色图像仍缺少完善的边缘检测算法。彩色图像的边缘不仅仅是图像中亮度产生突变的区域,还应包括色调和饱和度突变区域[4]。彩色图像携带有更多信息,在计算机视觉领域具有重要意义。彩色图像与灰度图像相比最重要的一个区别在于彩色图像的像素点由矢量描述,即红、绿、蓝3 个通道信息,而灰度图像的像素点是由一个数值描述其亮度信息。某些边缘在灰度图像中不好分辨,在彩色图像中却有着很强的辨识度。Novak 等[5]研究表明,彩色图像经过灰度化后,只保留原图像90%的边缘信息,但有10%的边缘信息在灰度化过程中丢失,这部分边缘由彩色信息决定,因此对于彩色图像的边缘检测不容忽视。此外,目前已有的彩色图像边缘检测算法在兼顾混合噪声抵抗和边缘检测完整性和连续性方面不够完善。因此,寻求一种鲁棒性能强,又能得到完整性、连续性较好的彩色图像边缘检测算法是目前机器视觉领域一个亟需解决的难题之一。
目前,彩色图像边缘检测算法可大致分为基于改进Canny 的边缘检测算法[6-10]、非Canny 框架下基于颜色梯度的边缘检测算法[11-12]、基于人工神经网络和群智能的边缘检测算法[13-15]3 类。基于改进Canny 的边缘检测是目前的一个研究热点,例如Zeng 等[6]首先利用矢量总变分模型代替高斯滤波去除彩色图像中的噪声,然后在CIE lab 颜色空间计算Sobel 颜色梯度和方向以用于非极大值抑制等后续处理。该方法虽然能够检测图像的主要边缘,但由于只计算了水平、垂直方向的色差,丢失掉了部分边缘方向信息,不利于后续的边缘精确定位;Chu 等[7]基于双色反射模型提取彩色图像的饱和度、色调两个不变量计算边缘梯度的幅值和方向,并嵌入到Canny 框架中实现边缘检测。该方法对混合噪声抵抗性较差,很多重要边缘并未检测出来;Mansoor[8]将图像的亮度分量和颜色分量加权融合在一起形成一幅新的图像,然后再利用Canny 算法对该图像进行边缘检测,实验结果表明该方法在梯度方向的精度和混合噪声鲁棒性方面得到了提高,但边缘检测的完整性较差。为了提高彩色图像的噪声鲁棒性,并保持其边缘探测器的高边缘分辨率,许多学者相继提出不同的解决方案。受各向同性和各向异性方向导数的噪声边缘检测器的启发,Li等[10]提出基于各向异性形态方向导数矩阵的抗噪声彩色边缘检测算法,利用计算得到的彩色图像的各向异性形态方向导数(Anisotropic Directional Derivatives,ANDD)矩阵,用于检测受高斯噪声或脉冲噪声污染的彩色图像边缘,同时对ANDD 矩阵作奇异值分解,提取彩色图像的彩色边缘强度图和彩色边缘方向图,然后将它们嵌入到Canny 检测路径中实现彩色图像边缘检测。该算法在噪声抵抗和边缘的检测性能上均有显著提升,但对于一些明显的颜色渐变区产生的边缘仍然会出现漏检问题。
关于非Canny框架下基于颜色梯度的边缘检测算法的研究也较多,例如Krishna 等[11]提出对受到噪声污染的彩色图像的R、G、B 三分量进行非线性预滤波处理,以减少噪声干扰,然后采用逐块旋转的方式在多个方向上定位边缘,并通过形态学细化处理得到最终边缘;Akinlar 等[12]提出一种彩色边缘绘制(ColorED)的边缘检测算法,该方法的预处理部分与Canny 算法类似,也是对彩色图像进行高斯平滑处理,然后计算梯度和方向,并根据梯度图的峰值确定一组稳定的边缘点(称之为锚点)。与Canny 不同的是,其是由智能路由算法以单像素宽度直接连接绘制锚点之间的边缘。该算法的优点是可以保证得到的边缘连续,但抗噪声能力以及弱边缘检测能力较差。
随着机器学习技术的不断发展,近年来出现了基于人工神经网络的边缘检测算法。例如,Liu 等[13]通过深度卷积神经网络的学习得到丰富的图像多尺度混合特征以实现边缘检测;Li 等[14]提出基于3 层小规模神经网络的边缘检测算法,其输入层为ANDD 矩阵,输出层只有一个神经元反映待检测像素是否属于真正边缘,取得了较好的检测结果。虽然该类方法可以得到较好的检测性能,但需要大量样本的训练学习,且边缘检测器性能依赖于学习样本的选取。另一种新颖的基于群智能优化的边缘检测方法是基于蚁群优化的边缘检测算法[15],该算法虽然有较高的运行效率和快速反应能力,不需要大量学习样本,但噪声抑制性能较差,对于图像中对比度较低的区域,极易产生边缘漏检现象且对细节边缘的抑制性较差。
由以上研究现状可知,非Canny 框架下的边缘检测算法复杂度较高,且具有较低的抗噪声性能;而基于神经网络或群智能计算的边缘检测算法需要进行大量学习样本的训练,学习过程较为复杂和费时。为此,本文在Canny框架下提出一种改进彩色图像边缘检算法,以解决目前该方向存在的两个问题:①检测结果仍然存在有效边缘丢失问题;②现有算法对混合噪声鲁棒性差,会导致检测结果中含有大量噪声边缘。该算法首先利用改进的基于小波变换的去噪方法对图像进行滤波处理以去除图像中的混合噪声;然后将处理后的图像转换到ClE lab 颜色空间中,并对每个像素分别计算0°、45°、90°以及135° 4个方向上的色差变化,由此准确定位彩色边缘的最大梯度和方向;最后进行非极大值抑制等完成彩色图像的边缘检测,并通过对比实验验证了提出算法的有效性。
1 改进彩色图像边缘检测算法
为在保持Canny边缘检测算子优点的同时提高彩色图像边缘检测的能力和检测算法对混合噪声的抵抗能力,本文在Canny 框架下提出一种改进彩色边缘检测算法,其整体流程如图1 所示。改进部分主要包括两个核心模块,一是基于改进小波变换的混合噪声去除,二是ClE lab 颜色空间中的多方向色差计算。以下具体介绍这两个模块的实现过程。
1.1 基于小波变换的混合噪声去除
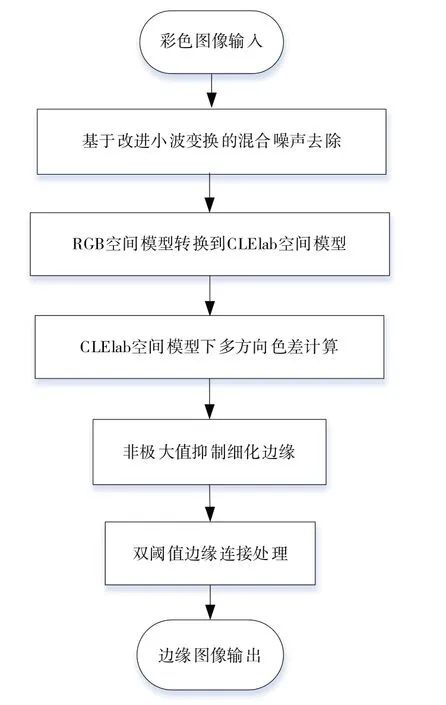
Fig.1 Flow of the improved color image edge detection algorithm图1 改进彩色图像边缘检测算法流程
对于混合噪声(高斯噪声和脉冲噪声)污染的图像,本文采用改进小波阈值去噪与自适应中值滤波相组合的方式进行去噪,主要包含以下两个步骤:①采用db 系列小波基对彩色图像RGB 三分量分别进行三层小波分解,然后采用改进的小波阈值法对每层的高频子带系数进行滤波,以去除高斯噪声;②对处理后的小波子带进行反变换重构,并对重构后的RGB 分量再分别进行自适应中值滤波,以去除椒盐噪声(脉冲噪声)。
小波阈值去噪的基本原理为含有噪声的图像经过多层小波分解后,图像中有效信息和噪声对应的小波系数会呈现不同的变化特征。在高频子带中,图像边缘、纹理对应的小波系数一般较大,而高频噪声对应的小波系数则一般较小。因此,通过选取合适的阈值函数对高频子带进行阈值处理,可实现去噪目的。
对于改进小波阈值去噪方法来说,含有混合噪声的彩色图像可以表示为原始图像加上随机混合噪声,为:
式中,F、S和n分别表示噪声污染图像、纯净图像和噪声信号,去噪的思想是将S和n分离开来。
小波去噪的关键是确定合适的阈值函数。传统小波阈值函数采用Donoho 等[16]提出的硬阈值函数和软阈值函数,但硬阈值函数会导致重构后的图像产生伪吉布斯效应和振铃效应,而软阈值函数由于重构后的小波系数与估计小波系数之间存在一个恒定偏差,会导致去噪后的图像过于平滑和模糊。为克服以上问题,目前常用的两种改进算法为:
(1)文献[17]提出的改进阈值函数。表示为:
式中,x为噪声图像下的原始小波系数,y为经过阈值函数处理后的小波系数,k为调节因子,λ为确定阈值。当|x| ≤λ时,并未将系数直接置为0,而是进行了线性压缩,避免了对系数的过渡扼杀。但当|x| >λ时,分解后的小波系数和处理后的小波系数之间存在恒定偏差。
(2)文献[18]提出的改进阈值函数。表示为:
该阈值函数满足连续性,当函数在|x| >λ时消除了恒定偏差的问题。但当函数在|x| ≤λ时直接将系数置零,对系数产生过渡扼杀,不利于细节的保留。
针对以上两种改进阈值函数存在的一些问题,本文希望阈值函数能够保证:①当|x| >λ 时,去噪后的小波系数能够尽快逼近原始图像的小波系数;②当|x| ≤λ 时,对小波系数线性压缩而非直接置零,以保留更多细节。
为此,本文提出一种新的阈值函数,表示为:
式中,=0.2(m-λ),m 表示原始小波系数中小波系数绝对值的最大值,以xmax表示。该阈值函数在区间[0,λ]内对原始小波系数按幂函数快速压缩,而不是直接置零,避免了对原始小波系数的过渡扼杀。当|x| >λ时,根据小波系数中绝对值的最大值m和阈值λ两个参数,共同控制幂函数快速逼近原始图像小波系数,使得函数有更好的自适应能力。
小波阈值λ的选取对于图像去噪效果也起着至关重要的作用,阈值过大会导致图像中的一些重要信息被过滤掉,阈值过低不利于噪声去除,选择阈值应随着小波分解级数的增加而降低。为此,本文采用文献[19]提出的阈值设定方法,表示为:
式中,i为小波分解尺度,σ为噪声标准差,S为图像大小,λ为第1 层小波分解尺度下的高频系数阈值,σ定义为:
式中,x1表示在第1 层小波分解尺度下的高频系数,median(|x|)表示对x矩阵取中值运算,0.6745 为高斯噪声标准方差的调整系数。
本文阈值函数与两种改进阈值函数曲线比较见图2。
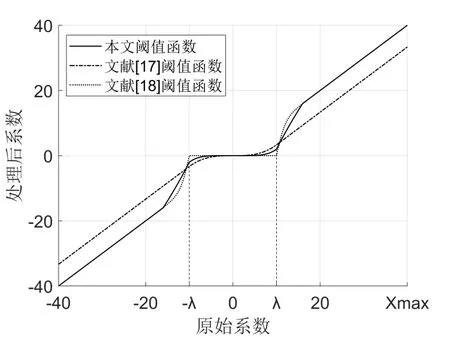
Fig.2 Comparison of three improved threshold function curves图2 3种改进的阈值函数曲线比较
图3 为本文改进小波阈值去噪方法和文献[17]、[18]中小波阈值去噪方法的比较结果,其中加入高斯噪声的均值为0,方差为0.02,各图下方的数字为其对应的 PSNR值。可以看出,本文算法在去除高斯噪声和保持边缘能力方面的效果优于另外两种算法。
小波阈值去噪方法能较好地去除图像中的高斯噪声,但如果仅用小波阈值去噪的方法去除图像中的混合噪声,处理后的图像仍然残留噪声点,主要原因是经过小波变换后的脉冲噪声在小尺度上较大,不能用阈值进行量化[20]。为了更好地去除这些残留噪声点,本文采用自适应中值滤波的方式。自适应中值滤波的主要思想是根据噪声的密度改变滤波窗口的大小,同时对信号点和噪声点采取不同的处理方法,即对于信号点保持灰度值不变,对于噪声点则用中值滤波代替。
假设fij表示图像在点(i,j)的灰度值,Aij表示当前工作窗口,fmax、fmin和fmed分别表示在Aij中的灰度最大值、灰度最小值和灰度中值,为预设的允许最大窗口。自适应中值滤波算法的基本步骤为:
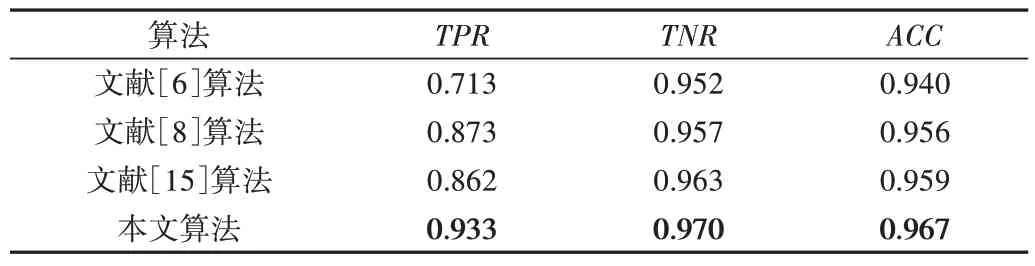
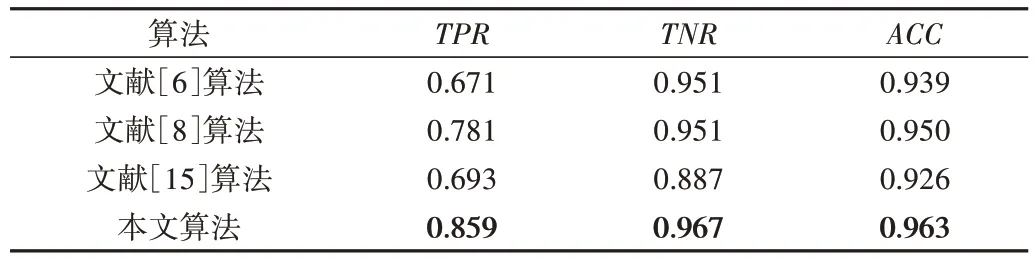
(1)判断是否满足条件fmin (2)判断是否满足条件fmin 该算法首先以fmin 为了精确定位彩色图像的边缘,对于经过以上滤波处理后的彩色图像,本文将其由RGB 颜色空间转换到ClE lab颜色空间中。首先将RGB 转ClE XYZ,公式为: 然后将ClE XYZ 空间转换到ClE lab 颜色空间中,转换方式为: 式中,x0=95.047,y0=100,z0=108.883,L表示亮度值,a,b表示色度值。 在ClE lab 颜色空间中,两个像素间色差的计算公式为: Fig.3 Performance comparison of three de-noising algorithms based on wavelet transform图3 3种小波去噪算法性能比较 式中,m、n和p、q表示该像素点在图像中的位置坐标,L表示该像素点的亮度值,a、b表示该像素点的色度值。 文献[6]中的算法在计算色差方向角时仅能计算到90°-180°方向之内的色差方向角,而无法计算到0°-90°方向内的色差方向角,易丢失边缘梯度信息,也不利于后续的非极大值抑制。针对以上缺点,本文在文献[6]的基础上增加Sobel 算子模板数量,即增加45°和135°两个方向的模板,并在4 个方向梯度模板的基础上进行色差幅值和角度计算,在一定程度上可以解决原算法在计算方向时的局限性。 图4 为本文定义的4 个方向对应的色差计算模板,目标点对应的4 个方向梯度幅值D0、D45、D90、D135的计算方法为: 目标点的梯度幅值计算方法为: Fig.4 Color difference calculation templates of 4 directions图4 4个方向色差计算模板 目标点的梯度方向θ取D0、D45、D90、D1354 个方向梯度幅值最大时对应的方向角度,在得到目标点的色差幅值以及方向角之后即可进行后续的非极大值抑制细化边缘和双阈值边缘连接处理。为更好地理解本文算法的整体流程,现给出算法的伪代码如下所示: 为验证提出算法的有效性,对大量彩色图像进行了边缘检测验证,并与文献[6]、文献[8]以及文献[15]中的算法进行比较实验。本文选取一种具有代表性的合成色块图像和边缘检测常用测试图片青椒作为对比展示,结果如图5 所示。文献[6]算法利用矢量总变分模型代替高斯滤波去除彩色图像中的噪声,然后在CIE lab 颜色空间计算Sobel 颜色梯度和方向以用于非极大值抑制等后续处理;文献[8]将图像的亮度分量与颜色分量加权融合在一起形成一幅新的图像,然后再对该图像利用Canny 算法进行边缘检测;文献[15]采用引导图像滤波和增强的蚁群优化方法来检测边缘。由于文献[6]并未给出具体双阈值参数设定方案,为体现公平性,本文算法以及对比算法均采用文献[8]给出的双阈值参数设定方案,表示为: 式中,TH表示高阈值,TL表示低阈值,γ、σ分别表示彩色图像对应的灰度图像的均值和方差。 图5 中的含噪图像均为对原图加入均值为0,方差为0.02 的高斯噪声和椒盐噪声。可以看出,在不考虑噪声影响的情况下,文献[6]算法在色差角度90°-180°内,即边缘沿着0°-90°走向时无法进行非极大值抑制,导致该走向内的边缘检测结果较粗,边缘定位不准确。文献[15]提出的蚁群算法对边缘细节的抑制较差。同时,文献[6]、[8]以及[15]的算法有很多重要的边缘产生了漏检现象,且检测出的边缘连续性较差,有明显断裂现象(见图5 红色标注)。在考虑到混合噪声影响的情况下,文献[6]、[15]算法在抗噪性能上较差,文献[8]的算法虽然抗噪性较好,但有很明显的边缘漏检现象。 综上所述,从边缘检测效果的完整性和抗噪性来看,本文算法具有明显优势。 Fig.5 Comparison of edge detection results for color images图5 彩色图像边缘检测结果比较 为了客观、定量地进行性能比较,采用TPR(查准率:边缘点检测的准确率)、TNR(查全率:背景点检测的准确率)和ACC(边缘检测的整体精度)3 个指标进行评判,其定义如下: 式中,TP(真正类)表示实际为边缘点,也被检测为边缘点的点数目;TN(真负类)表示实际为背景点,也被检测为背景点的数目;FP(假正类)表示实际为背景点,但检测成边缘点的点数目;FN(假负类)表示实际为边缘点,但检测为背景点的数目,即漏检的数目。以上3 个指标越高越好。 选取50 幅图像作为测试图,求取各算法的上述3 项指标,并对其做统计平均。4 种检测算法的统计结果如表1-表2 所示。表1 为不含噪声污染的图片检测性能指标;表2为含噪声污染的图片检测性能指标,其中所有含噪测试图片均加入均值为0,方差为0.02 的高斯噪声和椒盐噪声。由表1 可知,在不含噪声的情况下,本文算法较文献[6]、文献[8]和文献[15]算法查准率提高了3%~19%,查全率提高了1.3%~1.8%,边缘检测整体精度提高了1.1%~2.7%。由表2 可知,在含噪声的情况下,本文算法较其他算法查准率提高了3.8%~14.8%,查全率提高了1.6%~8%,边缘检测整体精度提高了1.3%~3.7%。综上所述,本文算法的3个性能指标优于其他对照算法,具有较高的边缘点检测准确率和精度。 Table 1 Edge detection performance comparison for no noise images表1 不含噪声图像边缘检测性能指标比较 Table 2 Edge detection performance comparison for noise pollution images表2 含混合噪声图像边缘检测算法性能指标比较 本文提出一种彩色图像边缘检测算法,首先通过改进小波变换阈值函数对原始图像进行滤波处理,既能保持边缘,又可以去除混合噪声;然后采用4 方向梯度模板计算滤波后的图像在CLELab 颜色空间模型下的多方向色差幅值和方向角,可以很好地抑制边缘漏检问题,使得检测出的边缘连续性较好,有效解决了色差方向角属于90°-135°范围时无法计算的问题。本文主要是对彩色图像的边缘检测算法进行研究,注重于对受到混合噪声污染的图像进行边缘检测,保证其检测结果的连续及完整性。由于本文是在Lab 颜色空间下计算局部图像亮度特征和对颜色特征进行色差梯度计算,下一步深入研究的方向是结合图像具体语义特征对边缘检测的图像进行细节处理,去掉其他无用的边缘信息,保留有利的边缘信息,以保证边缘检测结果更加符合人眼视觉特征。1.2 ClE lab颜色空间中多方向色差计算


2 实验结果与分析

3 结语

