基于协整理论的滚动轴承一致性退化特征提取

马新娜，刘心茹，牛天云，赵尚军，栾浩楠

（1.石家庄铁道大学 信息科学与技术学院；2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043）

0 引言

滚动轴承作为机械设备中的关键部件，常因故障导致整个机械设备停止运行。由于对轴承进行定期检查和维护需要投入大量人力物力，因此状态监测成为保障设备安全、稳定的关键［1］，国内外诸多学者在滚动轴承振动信号特征提取技术和性能退化评估模型方面进行了大量研究［2］。

赵志宏等［3］设计一种可有效提取轴承状态特征的深度可分离卷积自编码器模型，对XJTU-SY 滚动轴承加速寿命试验数据集构建健康指标，获取的健康指标单调性较好，可反映轴承退化至完全失效的趋势；刘晨辉等［4］提出基于混合域相对特征和FOA-XGBoostd 的滚动轴承退化评估方法，对PHM2012 加速寿命实验数据集同一工况下的振动信号进行特征提取；尹爱军等［5］提出深度概率优化的VAE 轴承状态评估方法，对Cincinnati 大学IMS 实验室滚动轴承加速退化实验数据中同一工况下的轴承进行实验，结果表明，其退化指标曲线变化趋势更清晰地说明了轴承退化过程。近几年，基于协整理论的性能退化评估方法得到了快速发展，利用协整关系可消除环境等因素引起的数据非平稳性，具有原理简单、易于实现的特点［6］。李耀龙等［7］提出一种基于协整理论的滚动轴承退化特征提取方法，所提取的特征能够将不同的滚动轴承全寿命数据统一起来，得到具有一致性的演变过程；杜望等［8］提出协整理论和向量误差修正模型预测滚动轴承性能退化趋势，首先检验3 种时域特征指标的平稳性及单整阶数，若各特征是同阶单整的，则进行协整检验，然后建立向量误差修正模型，进而预测其剩余使用寿命。在结构健康监测方面，何浩祥等［9］提出一种基于协整理论的桥梁频率识别方法，检验各变量的平稳性及单整阶数，并对同阶单整的变量进行协整检验，从而明确各变量之间长期、稳定的均衡关系，确立多因素之间的数学模型；Huang 等［10］将结构模态频率之间的协整系数作为卡尔曼滤波状态向量，通过观察协整关系的改变实现在线损伤预警，并将该方法应用于国内天津永和大桥检测，成功识别了两种结构损伤工况。

然而，在不同的轴承状态监测数据中，同一表征滚动轴承健康状态的退化特征往往表现出不同的变化趋势，也不具有一致的演变过程。因此，将多种不同工况、不同轴承间的轴承状态监测数据综合统一起来，寻找统一的变化规律，得到一致的退化特征是十分有意义的。

针对此问题，笔者选用多个实验室不同工况下的轴承全寿命数据，对其提取多种时域、频域以及复杂度特征，然后运用协整理论对特征进行分析，并提取基于协整理论的滚动轴承退化特征，接着对其两段性和一致性进行评估，最终得到具有泛化性和普适性的滚动轴承一致性退化特征。

1 基本理论

1.1 协整理论

时间序列若经过d -1阶差分仍不平稳，经过d阶差分才平稳，则称序列是d阶单整的，记作I(d)［11］。通常用单位根检验并判断时间序列的平稳性，常用的单位根检验方法有ADF（Augmented Dickey-Fuller）检验，当检验存在单位根时，时间序列是非平稳的。

协整意味着单整序列之间存在长期稳定的均衡关系，或者说存在特定的内在均衡机制维持着单整序列之间的长期稳定关系，非平稳时间序列之间这种长期稳定的均衡关系就是典型的协整关系［12］。Engle 等［13］给出的协整定义是：由n组d阶单整序列组成的向量yt=[y1t，y2t，…，ynt]T，如果存在一个向量β=[β1，β2，…，βn]使得线性组合βyt=β1y1t+β2y2t+…+βnynt是d-b阶单整，其中b>0，则认为yt=[y1t，y2t，…，ynt]T是(d，b)阶协整，记为yt～CI(d，b)，向量β称为协整向量［14］。常见的协整关系为CI(1，1)。为检验两个变量和是否具有协整关系，Engle 等于1987 年提出两步检验法，称为EG 检验，其是一种基于回归残差的检验［15］。首先，若xt和yt是一阶单整I(1)序列，用普通最小二乘法（Ordinary Least Squares，OLS）对回归方程yt=α+βxt+et（也称为协整回归方程）进行估计，得到残差序列。然后，检验残差序列et的平稳性，若et为平稳的，则xt和yt是协整的，反之则不是协整的。

1.2 一阶差分绝对和

在时间序列分析过程中，经常会用到差分运算。对于时间序列{xt}，差分运算可表示为Δxt=xt+1-xt(t=0，1，2，……)。其中，Δ 为差分算子。一阶差分可反映出时间顺序上相邻或邻近数据的波动幅度，在大多数情况下，相邻或邻近数据的波动方向并不重要，所以使用一阶差分绝对值。文献［16］总结了一阶差分绝对值的特性，虽然一阶差分绝对值可较好地表征时间序列的即时波动，但不能表征一组时间序列数据的总体波动。因此，引入一阶差分绝对和，其计算公式为：

1.3 p分位数

分位数是指将一个随机变量的概率分布范围分为几个等份的数值点，表示在该样本集中从小到大排列之后小于某值的样本子集占总样本集的比例，常用的有中位数（即二分位数）、四分位数、百分位数等。n个样本的p分位数xp具有以下两个性质［17］：一是有np个观察值小于或等于xp；二是有n(1 -p)个观察值大于或等于xp。xp的求解方法如下：

2 特征提取

2.1 振动信号基本特征提取与分析

有效的退化特征是实现轴承故障预测与健康管理的前提，周建民等［2］将振动信号的特征分为时域、频域、熵等。本文将以来自IEEEPHM2012 提供的轴承全寿命数据集中负载4200N、转速1652rpm 工况下Bearing2_1 垂直方向的振动信号为例，提取时域特征的一阶差分绝对和、均方根值、峰度、偏度、0.1 分位数、波形因子、峰值因子、脉冲因子，频域特征的频谱质心、频谱方差、频谱偏斜度、频谱峭度、傅里叶变换系数，以及熵特征的近似熵、分组熵、样本熵、置换熵。

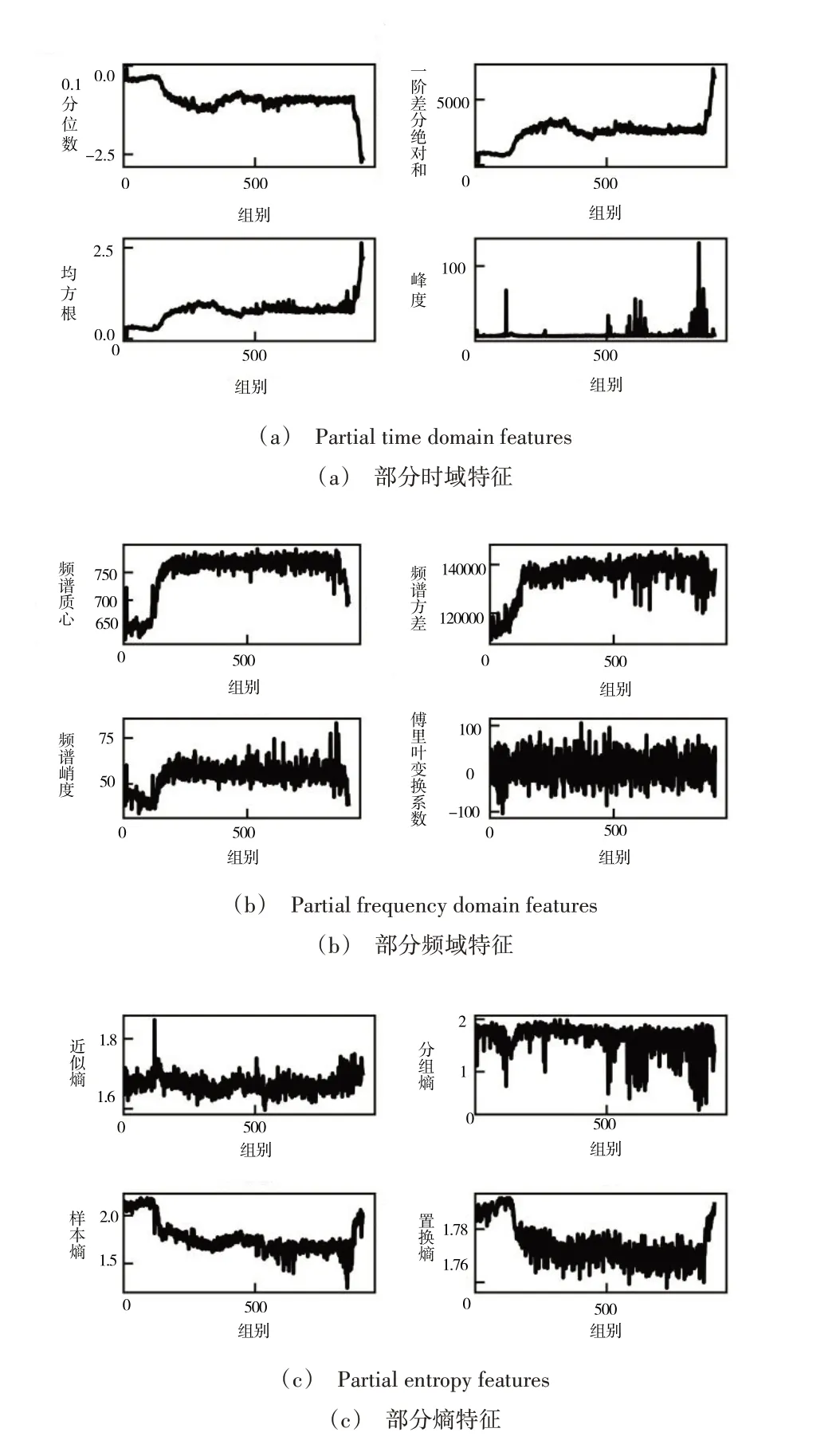
Fig.1 Bearing2_1 basic features图1 Bearing2_1基本特征

将提取的部分特征绘制成图像，如图1 所示。从图中可以看出，不同特征对轴承运行状态的反映差别较大，不仅在趋势项上表现不同，而且在数值上也表现出较大差异［18］。因此，需要找到一个能较好表征和评估轴承退化状态的一致性特征。对多个实验室多个工况下的轴承全寿命数据提取上述特征，通过初步实验发现，时域中的一阶差分绝对和可较好地表示滚动轴承退化过程，而时域中的p分位数总是与一阶差分绝对和保持相同或相反的变化趋势。进一步通过单位根检验和协整检验实验验证了一阶差分绝对和与p分位数之间具有协整关系，且协整融合后的特征具有较好的两段性和一致性。

2.2 基于协整理论的滚动轴承退化特征提取方法

对Bearing2_1 垂直方向的振动信号提取0.1、0.2、0.3、0.4、0.6、0.7、0.8、0.9 分位数，其特征如图2 所示（彩图扫OSID码可见，下同）。从图2 可以看出，0.1-0.4 分位数特征曲线的变化趋势一致，总体呈下降趋势，而0.6-0.9 分位数则与之相反。对各特征进行ADF 检验，并分别与一阶差分绝对和进行协整检验，得到协整特征。对协整特征的单调性和趋势性进行计算，结果如表1 所示，值越接近1 说明特征相应的性能越好。可以看出，0.1 分位数与0.9 分位数所得特征的性能差别不大，但是0.1 分位数所得特征的单调性和趋势性之和略高于0.9 分位数。另外，0.9 分位数与一阶差分绝对和有着相同的变化过程，而0.1 分位数与一阶差分绝对和有着相反的变化过程，二者之间有着更明显的长期、稳定的均衡关系。经综合考虑，本文选用p分位数中的0.1 分位数与一阶差分绝对和进行基于协整理论的滚动轴承退化特征提取。

Fig.2 Bearing2_ 1 p quantile feature图2 Bearing2_1 p分位数特征

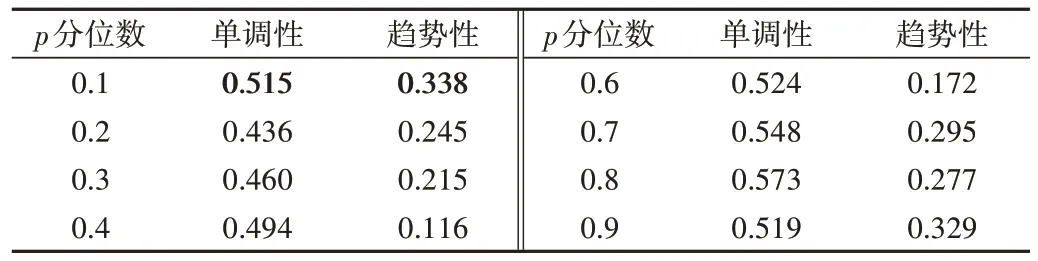
Table 1 Performance index of cointegration features with different quantile表1 不同分位数协整特征性能指标

0.1 分位数与一阶差分绝对和的基于协整理论的滚动轴承退化特征提取方法具体步骤如图3 所示。首先，对滚动轴承原始振动信号提取基本特征0.1 分位数与一阶差分绝对和，得到长度为m 的两个特征序列。然后，对长度为m 的特征序列分别进行ADF 检验，如果两个特征序列的单整阶数不同，则减小二者的长度并再次检验，重复此操作直到二者为同阶单整；如果两个特征序列为同阶单整，则进行协整检验，若检验结果表明两个特征序列之间不存在协整关系，则减小二者长度并再次检验，重复此操作直到二者之间存在协整关系。由于经过初步实验已确定0.1 分位数与一阶差分绝对和之间具有协整关系，因此特征序列减小的长度不会太大，以保证特征的泛化能力。接下来对存在协整关系的特征序列计算协整向量并得到协整特征，之后根据得到的协整向量将不具有协整关系的特征序列进行线性组合，即可得到基于协整理论的滚动轴承退化特征。为了消除波动的方向性，对其取绝对值，可得到最终的一致性退化特征。

Fig.3 Rolling bearing degradation feature extraction method based on cointegration theory图3 基于协整理论的滚动轴承退化特征提取方法

3 实验验证及分析

3.1 实验数据集

为了验证基于协整理论所提取的特征具有更好的两段性和一致性，本文选择多个实验室多种工况下的轴承全寿命数据进行实验：①数据来源于IEEE PHM2012 Data Challenge，由FEMTO-ST 机构提 供［19］，选取工 况1 下 的Bearing1_1 作为测试集1，选取工况2 下的Bearing2_1 作为测试集2，选取工况3 下的Bearing3_1 作为测试集3；②数据来源于美国IMS 中心的全寿命实验数据集［20］，选取失效模式为内圈故障的Bearing1_3 作为测试集4；③数据来源于XJTU-SY 滚动轴承加速寿命实验数据集［21］，选取工况3下的Bearing3_1作为测试集5。各测试集详见表2。

Table 2 Experimental data set表2 实验数据集

3.2 基于协整理论的滚动轴承一致性退化特征提取

首先，对所有测试集提取一阶差分绝对和与0.1 分位数，各测试集特征曲线如图4 所示。从图4 中可以看出，各个测试集的特征曲线没有统一的形状，表现出不同的退化过程。其中，测试集1 的一阶差分绝对和先增大后减小，经过一段时间的平稳状态后再次增大，之后再次减小，表现出多次“愈合”现象和阶跃现象，最终在2753 组左右快速上升；测试集2 的一阶差分绝对和经过一段时间的平稳状态后，同样表现出反复上升再下降的过程，然后在894组左右快速上升；测试集4 和测试集5 的一阶差分绝对和整体上先处于平稳状态，之后迅速上升，仔细观察也可发现“愈合”现象。这是由于在运行初期，轴承还处于磨合期，尚未进入稳定运行阶段，所以有所波动。之后在接近失效时，轴承会变得越来越不稳定，波动也会更加剧烈，所以一阶差分绝对和会迅速增大。

体育不单是身体行为的展示，还是社会经济文化多方面融合的生活方式，体育素养涵盖认识与实践的各个方面，为全方位塑造人之主体提供多方面路径。“体育素养是指在先天遗传的基础之上，通过后天的体育教育对意识、行为、个性、品德等方面进行的身体文化和精神文化的内在综合塑造”[10]。体育以人类的先天能力为活动准则，在对人类身体现状改造的基础上，加以对精神思想的净化。向善的思维导向求真的能动实践，理性地认识客体自然的发展规律，在尊重肉身生理规律的前提下，践行身体文化与精神修养的综合性教育，塑造人类主动追求自我超越的主体本身。

对所提出的特征序列进行ADF 检验，判断其平稳性，并对同阶单整特征序列进行EG 检验，可知所有测试集的全部或部分序列间具有协整关系。进一步计算协整向量，并根据协整向量求得协整特征。对全部测试集提取协整特征，为了消除波动的方向性，对协整特征取绝对值，得到的最终结果如图5所示。

对比图4 与图5 可以看出，在不同实验室的不同工况下，轴承垂直振动信号所提取的一阶差分绝对和与0.1 分位数表现出不同的退化状态，没有一致的变化规律；而经协整融合后的特征具有明显的两段性，表现出一致的退化规律，且该协整特征可减少退化前期、中期的波动性，表现出平稳性。当轴承处于严重退化阶段时，协整关系消失，表现出非平稳性，并且仍具有一定的单调性。由此可见，本文方法在滚动轴承一致性退化特征提取方面有效。

3.3 结果分析

现对经过协整融合后特征表现出的两段性进行分析，以测试集2 为例。为更清晰地展示所提特征的优越性，将一阶差分绝对和与协整特征进行对比。由于二者量纲不同，需要对其进行归一化处理，如图6所示。

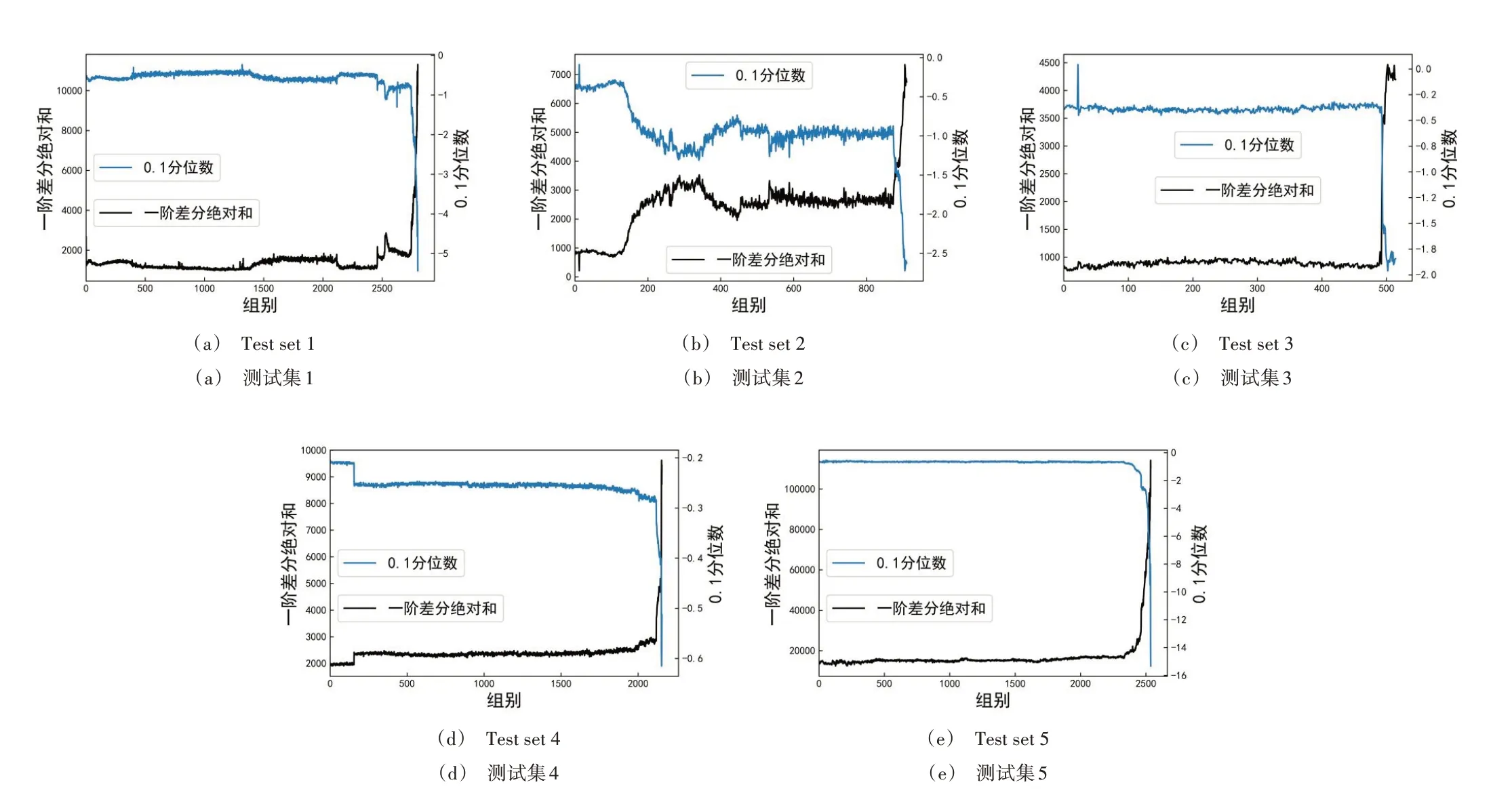
Fig.4 First difference absolute sum and 0.1 quantile feature curve of each test set图4 各个测试集一阶差分绝对和与0.1分位数特征曲线

Fig.5 Cointegration feature curve of each test set图5 各个测试集协整特征曲线

Fig.6 Comparison of first difference absolute sum and cointegration feature of Bearing2_1图6 Bearing2_1一阶差分绝对和与协整特征对比

测试集2 的一阶差分绝对和特征曲线展示了滚动轴承退化过程，包括从正常状态到轻微退化状态，再到中度退化状态以及失效状态的全过程。从开始运行至128 组，一阶差分绝对和保持平稳，轴承处于正常状态；在128-445组，一阶差分绝对和先持续上升，后逐渐下降，轴承处于早期故障状态；在445 组时，一阶差分绝对和开始上升，在小幅上升后平稳运行至527 组，又再次开始上升，同样经过小幅上升后平稳运行至873 组，在此阶段一阶差分绝对和出现了两次快速上升，表明轴承已进入中度退化状态；在873 组时，一阶差分绝对和迅速持续增大，表明此时轴承处于严重退化至失效的状态。

而对于所提出的协整特征，可看到具有明显的两段性，在894 组之前序列较平稳，波动性很小；从894 组到最后失效，序列快速上升。出现这种现象的原因是由于轴承在运行初期处于正常状态，波动正常，其一阶差分绝对和平稳，0.1 分位数也平稳；当轴承处于轻微退化阶段时，由于摩擦轴承表面产生突起，因此波动性变强，其一阶差分绝对和上升，同时由于波动变剧烈，轴承的振动幅度变大，导致0.1 分位数变小。当轴承表面的突起因故障加深而被磨平后，轴承波动性变小，一阶差分绝对和变小，轴承振幅也变小，进而0.1 分位数也变大。总体而言，在894 组之前，一阶差分绝对和与0.1 分位数之间保持着相反的变化趋势，使得二者的线性组合变得平稳。而当轴承严重退化至失效时，由于摩擦产生的突起迅速增多，波动性急剧增强，一阶差分绝对和迅速增大，0.1 分位数也开始减小。由于0.1 分位数的减小幅度不如一阶差分绝对和增加的幅度大，导致特征序列之间稳定的均衡关系消失，即协整关系消失，所提出的特征明显上升。

3.4 实验方案对比分析

为验证所提出的协整特征相比单独的一阶差分绝对和与0.1 分位数在一致性上的优势，采用动态时间规整（Dynamic Time Warping，DTW）算法［22］衡量特征的相似程度，也即一致性。按特征分别计算测试集两两之间的相似度，在计算前先对各特征进行归一化和平滑处理，对计算结果绘制热力图如图7所示。

各热力图关于y=-x 对称，且颜色越浅，表示相似度越高，一致性越好。可以明显看出，0.1 分位数的热力图颜色最深，一阶差分绝对和次之，而所提出协整特征的热力图颜色最浅，表明该协整特征有更好的一致性。

对3 种特征的5 个测试集分别计算相似度均值，结果如图8 所示。从图中可以看出，相较于单一特征，所提出的协整特征各个测试集的相似度均值最小，表明一致性最好。

按特征分别对5 个测试集所有的两两组合计算相似度均值、标准差等，计算结果如表3 所示。从表3 中可以看出，无论是均值、标准差、最大值、最小值还是其他统计量，所提出协整特征的相似度值都是最小的，表明其相较于单一特征有着较高相似度，具有较好的一致性。根据相似度均值来衡量，所提出协整特征的一致性为一阶差分绝对和的2.024 倍，为0.1 分位数的3.799 倍；根据标准差来衡量，协整特征的一致性为一阶差分绝对和的2.252 倍，为0.1 分位数的3.527倍。

基于协整理论的退化特征提取方法本质上也是一种特征融合方法。以测试集2 为例，对其一阶差分绝对和与0.1 分位数分别使用线性融合方法中的主成分分析（Principal Components Analysis，PCA）、局部保持投影（Locality Preserving Projections，LPP），以及非线性融合方法中的局部线性嵌入（Locally Linear Embedding，LLE）、等距特征映射（Isometric Mapping，Isomap）进行特征融合，融合后的结果如图9 所示。从图中可以看出，经过其他方法融合后的特征在总体上与单一特征曲线相似。由此可见，经PCA、LPP、LLE 以及Isomap 融合后的特征基本保留了单一特征的特性，而协整融合是把二者不同的特性进行融合，从而相互抵消，得到具有两段性的退化特征。

Fig.7 Similarity between features of each test set图7 测试集各特征间的相似度

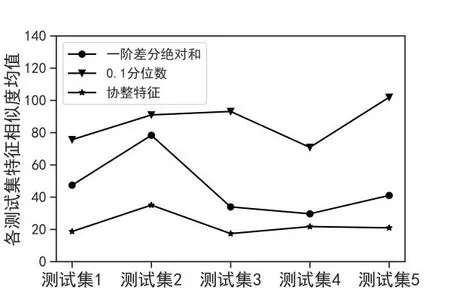
Fig.8 Mean value of feature similarity of each test set图8 各测试集特征相似度均值

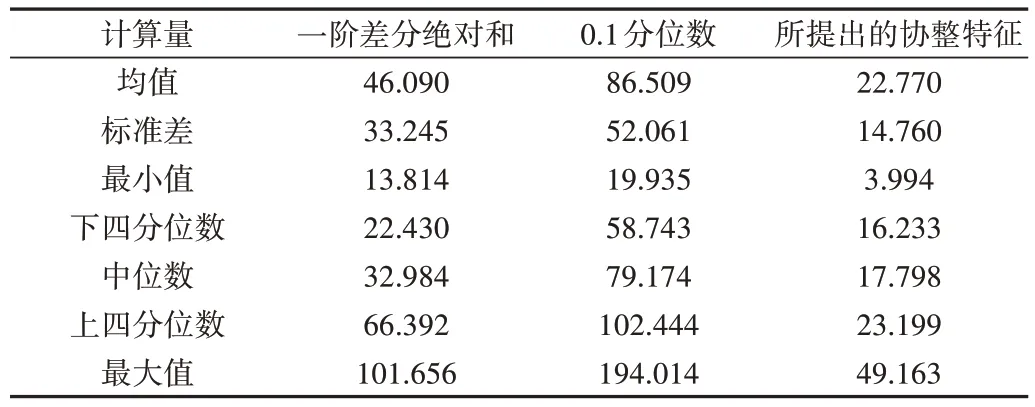
Table 3 Statistical value of similarity of non-repeated combinations of each test set表3 各测试集不重复组合相似度统计值

Fig.9 Fusion results of the first difference absolute sum and 0.1 quantile of test set 2 by other methods图9 测试集2一阶差分绝对和与0.1分位数经其他方法融合后的结果

4 结语

本文提出一种基于协整理论的滚动轴承一致性退化特征提取方法，经检验发现一阶差分绝对和与0.1 分位数之间存在协整关系，通过协整向量将二者线性组合得到协整特征。对不同实验室下的多组轴承全寿命数据进行协整特征提取，通过计算特征序列之间的相似性来度量一致性，结果表明协整特征的相似度值均小于单一特征，协整特征之间相似度的最小值为3.994，验证了其在一致性方面的优势；对比多种其他常用的特征融合方法，也验证了所提出的协整特征具有较好的两段性。通过协整，可有效降低单个特征在退化前期、中期的波动性，同时可有效减少来自工况、轴承等因素的影响，将不同的滚动轴承全寿命数据统一起来，得到具有一致性的演变过程，进一步得到滚动轴承状态监测数据一致性变化规律，这也是后期需要继续探索的方向。