基于GWO-VMD算法的齿轮故障自适应特征提取
崔乐晗,于洋
基于GWO-VMD算法的齿轮故障自适应特征提取
崔乐晗,于洋
(沈阳工业大学,沈阳 110870)
齿轮产生故障时,利用其声发射信号进行自适应特征提取后诊断。利用变分模态分解方法(VMD)对齿轮发生故障时的声发射信号进行分解。在现实状况中,采集声发射原信号噪声干扰大,导致特征提取准确度低,并且模态分解时参数需要人为调试设定。鉴于此,引入灰狼优化算法(GWO),对模态分解个数和二次惩罚因子自适应选择最优参数后,对信号分解得到本征模态函数(IMF)。通过相关系数选出最佳IMF作为特征分量,计算其峭度和样本熵。计算了各分量的相关系数,选取与原始信号最为相近的分量,分别计算其峭度和样本熵。分解后,齿轮故障声发射信号峭度高于正常的情况,而样本熵则偶然性表现为正常情况下的值大于故障条件下的值。采用支持向量机对特征向量集进行分类识别,对比改进后的试验结果,GWO-VMD结合峭度–样本熵的方法能够有效地提取故障特征,判断齿轮状态是否健康。
齿轮;声发射信号;变分模态分析;灰狼优化;峭度;样本熵;支持向量机
现今,智能化应用在航空、武器装备等各行各业中,所以零件的健康状况对设备的运行至关重要[1]。齿轮在工作中承受的压力较大,并且对啮合精度要求高,大部分设备离不开齿轮。据资料表明,设备中受到冲击的齿轮会导致设备整体的状况堪忧[2]。齿轮发生磨损的情况出现频繁,超过允许量或发生断裂等严重故障时,甚至对人身安全也有很大威胁。齿轮故障诊断提前预测可防止危险发生,还可节省不必要的支出[3]。考虑声发射技术反应时间短,还有包含信息量大[4]等优点,因此从齿轮声发射信号中提取出有效的故障特征,是识别出齿轮故障的重要前提,也是确保齿轮健康安全运行的关键。
引入声发射技术的早期,郑州工业大学的韩捷等[5]根据齿轮信号的特性(如故障成分较大、周期小)研究了故障信号频谱的原理,并总结了不同时期的齿轮频率特性。研究者们可以根据频谱图初步判断故障与正常齿轮的区别,但因为真实环境中噪声较大,结果会受影响。湖南大学的于德介等[6]将希尔伯特–黄变换方法引入齿轮箱故障诊断,对分解后的信号作希尔伯特变换来提取信号的特征,建立了基于齿轮故障振动信号的齿轮故障诊断模型,效果比小波分析好,但是噪声问题仍有较大影响。边杰[7]采用变分模态分解算法,结合1.5维普分析结果,能更有效地显示故障的冲击信号,比包络谱效果更优,但是模态分解中调参对信号分解较大,结果受到影响。长安大学的廖攀[8]通过对样本熵以及BP神经网络等进行研究,提出了声发射信号用于齿轮故障诊断的改进方向,将熵特点应用于故障特征提取中受到推广。齿轮的故障诊断问题一直是比较热点的研究课题之一,但是实际工作中现场情况复杂,采集到的声发射信号可能出现大量噪声,会淹没齿轮伤损信号。
以美籍华裔学者Norden E. Huang提出的经验模态分解(EMD)为代表的自适应信号分解方法近年来备受关注,在机械故障诊断领域已经取得了许多有益成果。不同于小波变换等传统的通过基函数展开的信号分解方法,EMD 是完全由数据驱动的,它既不需要构造任何先验基来匹配信号的特征结构,也不需要在时域、频域或时频域上施加任何约束,因而能够实现对任意信号的自适应分解。然而此方法迭代计算的运行效率较低,并且容易造成误差累积,会显著影响子信号的分解精度。因此,2014年,Dragomiretskiy等[9]提出了变分模态分解方法(VMD)。与EMD及其变体方法相比,VMD 具有完备的数学理论支撑,无需进行迭代求解,可以避免由迭代计算造成的误差累积,并有效解决了EMD等迭代算法效率低下的问题。
本文采用VMD自适应算法对采集的原始声发射信号去噪,其效果在抗模态混叠和抗虚假分量方面的优越性超过EMD、EEMD算法。用VMD算法对原信号进行分解时[10],参数选择是个难题,一般凭经验且手动调整参数,既费时,又低效[11]。因此,考虑到参数不合理带来的分解问题,引用灰狼优化算法参数寻优,达到信号自适应分解的最佳效果。再计算时域特征峭度和熵特征样本熵的值,根据其特性来判断针对齿轮声发射信号哪个效果更突出、稳定。最后,通过对比故障和正常模拟试验下的结果,可为现场进行设备齿轮故障诊断提供一定的参考。
1 灰狼优化变分模态算法及工作原理
1.1 变分模态分解基本原理







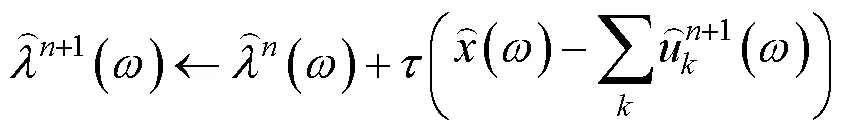
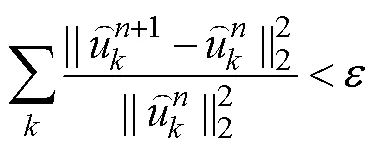
1.2 灰狼优化算法介绍



1)测量个体与猎物之间的距离,如式(10)所示。

2)更新灰狼位置。


式(11)、(12)中:为收敛因子;整个迭代过程中,的值在[2,0]线性变化,2为[0,1]的随机数。
3)猎物位置定位。当、和¶狼的位置更新后,取、和¶位置的平均值作为猎物的移动的方向,见式(13)。

1、2、3为根据式(11)、(12)更新后的、和¶狼的位置。
1.3 GWO-VMD流程
GWO-VMD的流程如图1所示。

图1 GWO优化VMD的参数流程
1.4 齿轮故障声发射试验
齿轮故障诊断采集系统如图2所示,硬件系统是QPZZ-Ⅱ型旋转机械振动和故障诊断试验平台。分批将正常和磨损故障齿轮更换到齿轮箱中,包含2个啮合齿轮。故障在大齿轮上,且齿数为75,小齿轮为55个齿数。平台运转过程中,由DS5声发射软件直接运行AE_DS5.exe,对采集到的齿轮正常和故障时的声发射信号进行波形提取。

图2 QPZZ-Ⅱ型旋转振动故障试验平台
2 结果及分析
2.1 声发射信号分解结果
试验中设置采样频率为3 MHz,门槛值为40 dB,电机转速为900 r/min,采集正常和故障工况下的试验数据。齿轮产生故障的特征频率的计算见式(14)—(16)[17]。



式中:1为小齿轮的齿数,1=55;2为大齿轮的齿数,2=75;为转速。根据式(14)—(16)可得出,在900 r/min的转速下,齿轮故障频率为11 Hz。试验正常和故障未处理原始声发射信号波形以及频谱如图3、图4所示。
由图3、图4可以看出,齿轮在正常时,频谱无明显变化。在故障状态下,对应的频谱图中在某个频率段出现了大量的冲击,对比正常状态幅值也大大增长。说明声发射应用于齿轮故障检测是有效的,对冲击信号很敏感。具体的信号隐藏信息还需进一步处理分析。
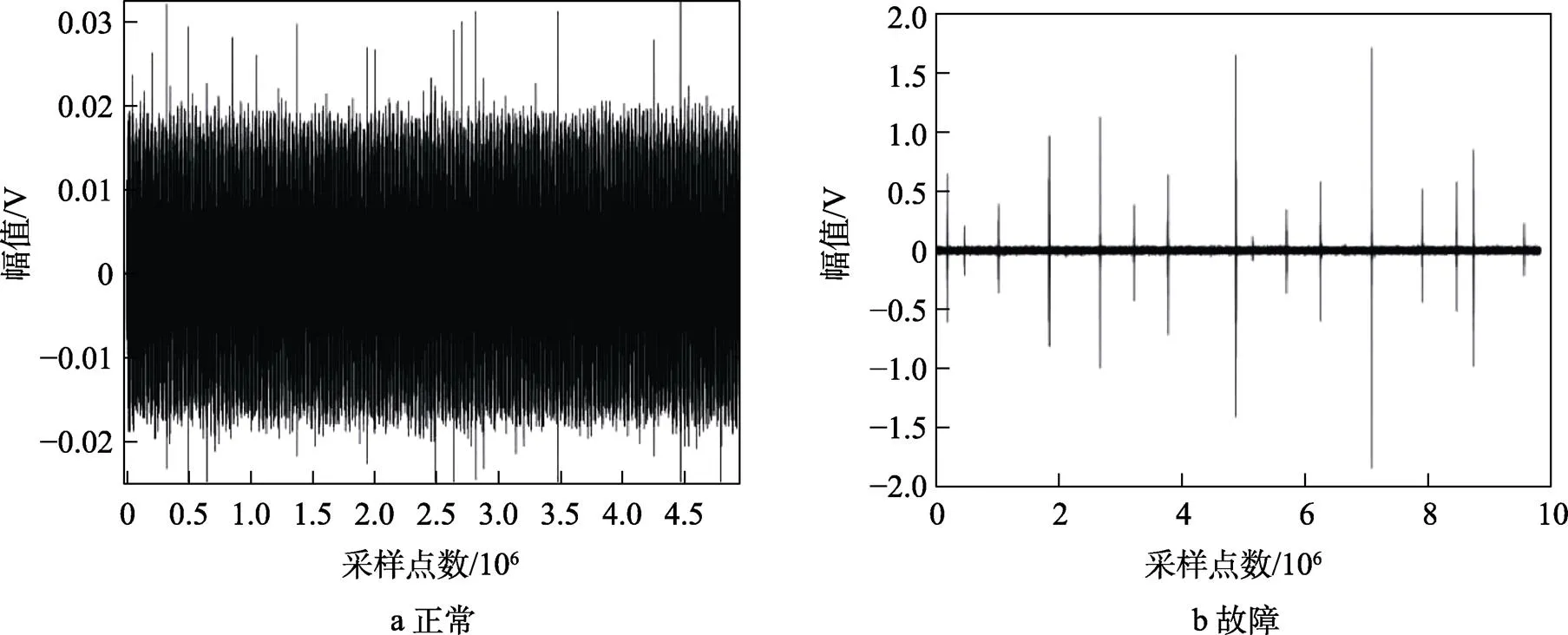
图3 声发射原信号波形
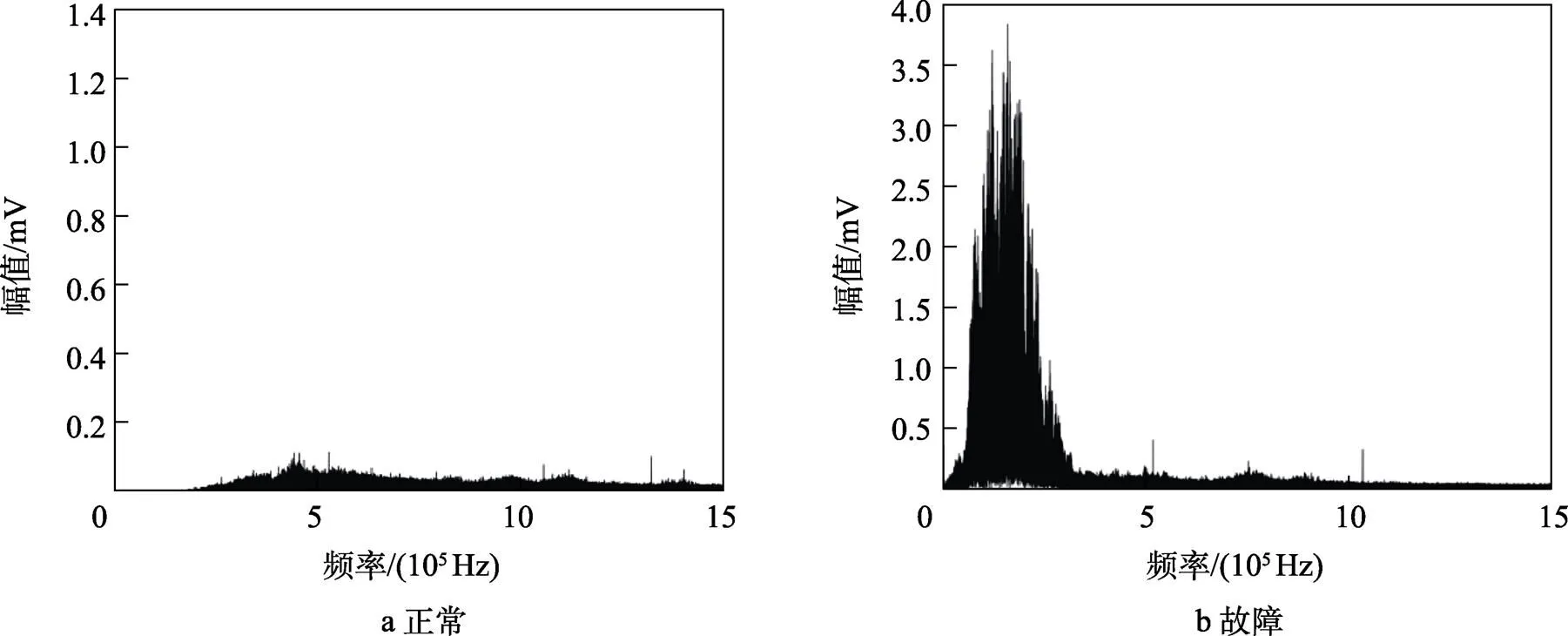
图4 声发射原信号频谱
验证试验采集齿轮故障声发信号征提取的可行性,使用GWO算法对VMD中的模态个数和惩罚参数寻优,结果见表1。
表1 不同工况下的最优参数

Tab.1 Optimum parameters under different conditions
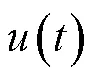
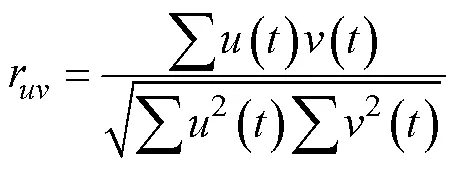
正常齿轮和故障齿轮各分量相关系数大小见表2。
表2 齿轮VMD分解后信号相关系数

Tab.2 Signal correlation coefficient after gear VMD decomposition
选取表2中最大的相关系数,正常齿轮选取IMF6,故障齿轮选取IMF8模态分量作为最佳分量,并对其做包络谱解调,如图5、6所示。

图5 齿轮VMD分解后波形

图6 波形的包络谱
由图5、图6可知,当使用GWO-VMD分解声发射信号后,正常齿轮根据相关系数原则选取IMF6对其做包络谱,可以发现正常情况下信号无明显冲击(100 Hz处为试验平台故障处,并非齿轮故障)。当磨损故障发生时,根据相关系数选取IMF8对其做包络谱,可观察到1处约为11 Hz,并且有倍频出现,与上文齿轮故障特征频率相对应,证明了GWO-VMD对信号分解的有效性。
2.2 特征提取
1)峭度。峭度[19]系数表示故障形成的大幅值脉冲出现的概率,对分量中冲击信号很敏感,计算公式如式(18)所示。
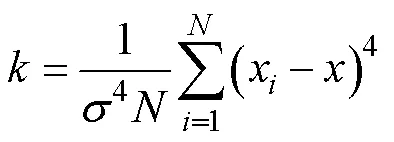
式中:为标准差;为信号点数;为期望值。
取1组正常和故障下齿轮所选分量的峭度进行对比,正常齿轮选择IMF6的峭度值为5.823,故障齿轮选择IMF8的峭度值为10.768。由上述所求峭度值可知,齿轮在故障时的峭度值明显比正常时大,符合峭度值的理论故障时冲击信号更加明显,峭度幅值更大。
2)样本熵。样本熵是基于近似熵的优化方法,在诊断病理状态等方面应用较多。样本熵值越低,序列的复杂性就越低;相反,当熵值越高,复杂度越高,从而拥有更好的噪声抑制性能[20]。样本熵不包含自身数据段的比较,已经广泛应用于信号研究中[21]。因为样本熵对数据长度的依赖性较小,在原数据中选取5 000个采样点,再次进行VMD分解正常齿轮和故障齿轮各分量相关系数的大小,选择IMF1分量。
取1组正常和故障下齿轮所选分量的样本熵进行对比,正常齿轮的样本熵为0.126,故障齿轮中通过VMD分解得到IMF1其样本熵为0.349。对比这2个数据可以发现,故障的样本熵大于正常信号,符合其原理。但是对多组样本处理时发现,偶尔会出现正常比故障样本熵更高的现象,导致样本熵值与声发射信号复杂度不一致的原因可能是阈值的设置。由于故障状态下声发射信号有周期性冲击幅值,该冲击幅值使阈值变大,则模式匹配时的相似容限变大,模式匹配值变大,计算得出的熵值变小,即故障状态障状态下声发射信号的复杂度低[22]。因此,将结合峭度–样本熵特征向量作为支持向量机的输入,并取200组样本以完善在实际应用中可能存在差异性采样的问题。
2.3 故障诊断
为了证明使用GWO-VMD结合其峭度–样本熵作为齿轮的故障特征向量集方法是有效的,引入支持向量机对正常和磨损故障下的齿轮特征向量集作分类识别。因为支持向量机具有良好的散失能力,在学习样本稀疏的环境中,依然能保持较高的分类准确度,受外界异常因素的影响不大,具有良好的性能[23]等特点,所以使用支持向量机实现了对齿轮的故障诊断。

2)故障诊断结果分析。分别使用支持向量机和灰狼算法优化后的支持向量机对样本进行训练,结果如图7—9所示。
通过测试集的实际分类和预测分类可以看出,优化前直接使用支持向量机算法对数据集处理时,得到测试集分类准确率为90.307 7%,错误分类样本为6个。图8中种群数量设置为20,终止进化代数设置为200。按图8使用优化后的参数值,根据GWO-SVM的试验结果,准确率为98.717 9%,错误样本为1个。由此可知,经过灰狼优化参数值后,支持向量机使得故障诊断的精确度更高,效果更好,并且说明了故障提取特征的有效性。
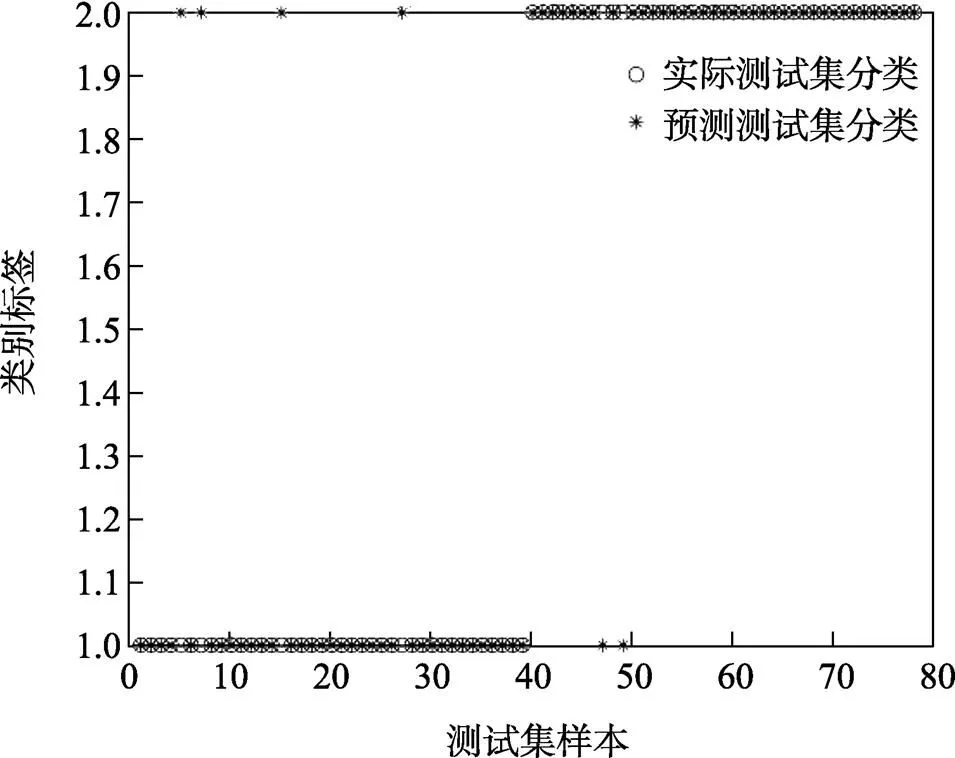
图7 支持向量机分类结果

图8 灰狼算法优化的参数值

图9 GWO-SVM分类结果
3 结论
1)本文通过引进灰狼优化算法对变分模态算法VMD中态分解个数和二次惩罚因子进行寻优,并且选择包络熵最小值作为适应度函数,可以自适应地完成信号分解,并且得到较优的结果,以避免通过人为观察法取值的主观误差。但是灰狼算法中收敛因子等参数的选取一般采用经验值取大致范围,因此还存在收敛过早,陷入局部最优的问题。
2)计算分解后IMF分量的样本熵值,会发现有的正常的样本熵大于故障的样本熵的值,考虑是受到样本熵中的阈值和相似容限的影响。对比试验分析结果,因为峭度的无量纲特性,与尺寸、旋转速度以及载荷分布等无关,计算出分量的峭度,对比正常和故障下的大小,取峭度值更适合作为齿轮声发射信号的特征向量。
3)将200组峭度–样本熵的特征向量集样本作为支持向量机的输入,测试集为40组,训练集为160组。由于惩罚因子和核参数的合理选取对分类结果有影响,再次利用灰狼算法改进支持向量机,其结果不仅说明了改进后的效果更好,准确度更高,也证明了GWO-VMD结合峭度–样本熵在特征提取方面的有效性。
[1] 鲁朝静. 齿轮箱复合故障诊断方法的研究[D]. 石家庄: 河北科技大学, 2018.
LU Chao-jing. Research on Compound Fault Diagnosis Method of Gear Box[D]. Shijiazhuang: Hebei University of Science and Technology, 2018.
[2] (日)丰田利夫. 设备现场诊断的开展方法[M]. 高克勣, 李敏, 译. 北京: 机械工业出版社, 1985.
TOYODA Akio. Methods of Equipment Field Diagnosis[M]. GAO Ke-ji, LI Min, Translated. Beijing: China Machine Press, 1985.
[3] 王靖岳. 随机扰动下齿轮传动系统的非线性动力学与故障辨识研究[D]. 沈阳: 东北大学, 2015.
WANG Jing-yue. Research on Nonlinear Dynamics and Fault Identification of Gear Transmission System with Stochastic Disturbance[D]. Shenyang: Northeastern University, 2015.
[4] 袁俊, 沈功田, 吴占稳, 等. 轴承故障诊断中的声发射检测技术[J]. 无损检测, 2011, 33(4): 5-11.
YUAN Jun, SHEN Gong-tian, WU Zhan-wen, et al. Acoustic Emission Testing Technology in Diagnosis of Bearing Failure[J]. Nondestructive Testing Technologying, 2011, 33(4): 5-11.
[5] 韩捷, 张琳娜. 齿轮故障的振动频谱机理研究[J]. 机械传动, 1997, 21(2): 21-24.
HAN Jie, ZHANG Lin-na. Study on Vibration Spectrum Mechanism of Gear Fault[J]. Mechanical Transmission, 1997, 21(2): 21-24.
[6] 于德介, 程军圣, 杨宇. Hilbert-Huang变换在齿轮故障诊断中的应用[J]. 机械工程学报, 2005, 41(6): 102-107.
YU De-jie, CHENG Jun-sheng, YANG Yu. Application of hilbert-Huang Transform Method to Gear Fault Diagnosis[J]. Chinese Journal of Mechanical Engineering, 2005, 41(6): 102-107.
[7] 边杰. 基于遗传算法参数优化的变分模态分解结合1.5维谱的轴承故障诊断[J]. 推进技术, 2017, 38(7): 1618-1624.
BIAN Jie. Fault Diagnosis of Bearing Combining Parameter Optimized Variational Mode Decomposition Based on Genetic Algorithm with 1.5-Dimensional Spectrum[J]. Journal of Propulsion Technology, 2017, 38(7): 1618-1624.
[8] 廖攀. 变速箱齿轮故障诊断系统研究[D]. 西安: 长安大学, 2018.
LIAO Pan. Research on Fault Diagnosis System of Gear in Gearbox[D]. Xi'an: Changan University, 2018.
[9] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[10] 卓仁雄, 肖金凤. 基于改进的集合经验模态分解的电动机滚动轴承故障诊断研究[J]. 机械制造与自动化, 2019, 48(1): 36-39.
ZHUO Ren-xiong, XIAO Jin-feng. Research on Fault Diagnosis Method of Motor Bearing Based on Improved EEMD and SVM[J]. Machine Building & Automation, 2019, 48(1): 36-39.
[11] JIANG Xing-xing, WANG Jun, SHI Juan-juan, et al. A Coarse-to-Fine Decomposing Strategy of VMD for Extraction of Weak Repetitive Transients in Fault Diagnosis of Rotating Machines[J]. Mechanical Systems and Signal Processing, 2019, 116: 668-692.
[12] ZHANG Xin, MIAO Qiang, ZHANG Heng, et al. A Parameter-Adaptive VMD Method Based on Grasshopper Optimization Algorithm to Analyze Vibration Signals from Rotating Machinery[J]. Mechanical Systems and Signal Processing, 2018, 108: 58-72.
[13] 赵玮. 基于VMD和FSK的齿轮箱早期故障诊断[J]. 机械传动, 2018, 42(1): 143-149.
ZHAO Wei. Early Fault Diagnosis of Gear Box Based on Variational Mode Decomposition and Fast Spectral Kurtosis[J]. Journal of Mechanical Transmission, 2018, 42(1): 143-149.
[14] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81.
TANG Gui-ji, WANG Xiao-long. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Xi’an Jiaotong University, 2015, 49(5): 73-81.
[15] 刘宁宁, 王宏伟. 基于改进灰狼优化算法的移动机器人路径规划[J]. 电测与仪表, 2020, 57(1): 76-83.
LIU Ning-ning, WANG Hong-wei. Path Planning of Mobile Robot Based on the Improved Grey Wolf Optimization Algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(1): 76-83.
[16] 罗佳, 唐斌. 新型灰狼优化算法在函数优化中的应用[J]. 兰州理工大学学报, 2016, 42(3): 96-101.
LUO Jia, TANG Bin. Application of Novel Grey Wolf Optimization Algorithm in Function Optimization[J]. Journal of Lanzhou University of Technology, 2016, 42(3): 96-101.
[17] 刘跃福. 齿轮传动系统的复合故障特征提取方法研究[D]. 沈阳: 沈阳理工大学, 2021.
LIU Yue-fu. Research on Composite Fault Feature Extraction Method of Gear Transmission System[D]. Shenyang: Shenyang Ligong University, 2021.
[18] 刘东瀛, 邓艾东, 刘振元, 等. 基于EMD与相关系数原理的故障声发射信号降噪研究[J]. 振动与冲击, 2017, 36(19): 71-77.
LIU Dong-ying, DENG Ai-dong, LIU Zhen-yuan, et al. De-Noising Method for Fault Acoustic Emission Signals Based on the EMD and Correlation Coefficient[J]. Journal of Vibration and Shock, 2017, 36(19): 71-77.
[19] 吴小涛, 杨锰, 袁晓辉, 等. 基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]. 振动与冲击, 2015, 34(2): 38-44.
WU Xiao-tao, YANG Meng, YUAN Xiao-hui, et al. Bearing Fault Diagnosis Using EEMD and Improved Morphological Filtering Method Based on Kurtosis Criterion[J]. Journal of Vibration and Shock, 2015, 34(2): 38-44.
[20] RICHMAN J S, MOORMAN J R. Physiological Time- Series Analysis Using Approximate Entropy and Sample Entropy[J]. American Journal of Physiology Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049.
[21] 赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J]. 振动与冲击, 2012, 31(6): 136-140.
ZHAO Zhi-hong, YANG Shao-pu. Sample Entropy-Based Roller Bearing Fault Diagnosis Method[J]. Journal of Vibration and Shock, 2012, 31(6): 136-140.
[22] 刘建昌, 权贺, 于霞, 等. 基于参数优化VMD和样本熵的滚动轴承故障诊断[J]. 自动化学报, 2022, 48(3): 808-819.
LIU Jian-chang, QUAN He, YU Xia, et al. Rolling Bearing Fault Diagnosis Based on Parameter Optimization VMD and Sample Entropy[J]. Acta Automatica Sinica, 2022, 48(3): 808-819.
[23] 岳应娟, 孙钢, 蔡艳平. 基于变分模态分解近似熵和支持向量机的轴承故障诊断方法[J]. 轴承, 2016(12): 43-46.
YUE Ying-juan, SUN Gang, CAI Yan-ping. Bearing Fault Diagnosis Method Based on VMD-AE and SVM[J]. Bearing, 2016(12): 43-46.
Adaptive Feature Extraction of Gear Fault Based on GWO-VMD Algorithm
CUI Le-han, YU Yang
(Shenyang University of Technology, Shenyang 110870, China)
The work aims to make use of the acoustic emission signal when fault occurs for adaptive feature extraction and diagnosis. The variational mode decomposition method (VMD) was used to decompose the acoustic transmission signal when fault occurs. In reality, collecting acoustic signal noise interference causes low feature extraction accuracy due to the large original noise interference, and mode decomposition parameters need artificial debugging set. The Gray Wolf Optimization (GWO) algorithm was introduced to obtain the intrinsic mode function (IMF) through signal decomposition after adaptive selection of optimal parameters for mode decomposition k and quadratic penalty factor. The peakedness and sample entropy were calculated by selecting the based on correlation coefficient. The correlation coefficient of each component was calculated. The peakedness and the sample entropy of the component most similar to the original signal were calculated respectively. After the decomposition, the gear fault acoustic emission signal was higher than normal, while the sample entropy was more than the normal value under the fault condition. Support vector machine is used to classify and identify feature vector sets. Compared with the improved experimental results, GWO-VMD combined with peakedness-sample entropy method can effectively extract fault features and determine whether the gear state is healthy.
gear; acoustic emission signal; variational mode decomposition; grey wolf optimization; peakedness; sample entropy; support vector machine
2022-03-12;
2022-03-31
CUI Le-han (1996-), Female, Postgraduate, Research focus: equipment fault diagnosis and monitoring.
于洋(1967—),女,博士,教授,主要研究方向为机械设备故障健康监测与故障诊断技术。
Corresponding author:YU Yang (1967-), Female, Doctor, Professor, Research focus: health monitoring and fault diagnosis technology of mechanical and equipment faults.
崔乐晗, 于洋. 基于GWO-VMD算法的齿轮故障自适应特征提取[J]. 装备环境工程, 2023, 20(2): 117-124.
TH165+.3
A
1672-9242(2023)02-0117-08
10.7643/ issn.1672-9242.2023.02.016
2022–03–12;
2022–03–31
崔乐晗(1996—),女,硕士研究生,主要研究方向为设备故障诊断及监测。
CUI Le-han, YU Yang.Adaptive Feature Extraction of Gear Fault Based on GWO-VMD Algorithm[J]. Equipment Environmental Engineering, 2023, 20(2): 117-124.
责任编辑:刘世忠

