基于SHCA-T算法的车身骨架多工况耐撞性优化设计*

段利斌，周华锦，杜展鹏，张雨，徐伟，刘星，江浩斌

（江苏大学汽车与交通工程学院，镇江 212013）

前言

车身骨架是汽车的主要承载结构，其结构耐撞性影响汽车的碰撞安全性。车身结构耐撞性优化是提高汽车碰撞安全性的重要手段，在汽车工业得到广泛应用。汽车碰撞仿真的输出响应非线性程度高且存在数值噪声和震荡，利用梯度优化算法很难有效解决车身结构耐撞性优化问题。由于汽车碰撞仿真计算时间长，利用进化算法（如遗传算法［1］）求解该问题则须进行数以千计的有限元仿真分析，导致优化时间非常漫长。基于代理模型的优化方法可大幅提高优化效率，是解决车身结构耐撞性优化问题的重要手段。典型的方法有HDMR 算法［2］、基于伪CEI 准则的并行EGO 算法（简称“并行EGOPCEI”）［3］等。王登峰等［4］建立了某轿车隐式参数化车身模型，以车身骨架的厚度为设计变量，开展了车身刚度、模态、碰撞性能的多工况优化设计。Chuang等［5］考虑车身刚度、NVH、碰撞等工况，以车身结构厚度为设计变量，结合代理模型和进化算法开展车身骨架的多工况优化设计。然而，当设计变量较多时（如超过30 个变量），基于代理模型的优化算法寻优效率则会大幅降低。

混合元胞自动机（hybrid cellular automata，HCA）方法考虑了材料非线性力学性能，以单元密度为设计变量，根据有限元仿真获得的元胞状态信息以及一定的控制规则进行元胞状态进化，适用于解决连续体结构的耐撞性拓扑优化问题［6-9］。近年来，一些学者对HCA 方法进行了改进，提出了以薄壁结构的厚度作为设计变量的改进HCA 方法。Duddeck等［10］以薄壁结构的厚度作为设计变量，构建了多胞薄壁结构的元胞自动机模型，提出了HCATWS 方法，开展了多胞薄壁结构的耐撞性拓扑优化设计，在花费少量有限元仿真的情况下得到了多胞薄壁结构的最优厚度。Duan 等［11］构建了VRB 结构的一维元胞自动机模型，提出了求解可轧制约束下VRB 结构最优厚度分布的混合元胞自动机算法（eHCAVRB）。然而，车身骨架是由大量薄壁结构装配形成的空间框架结构，其耐撞性优化设计属于离散型设计空间内的非线性动态响应优化问题。由于缺乏适用于车身骨架的元胞自动机（CA）模型，导致现有HCA 算法无法直接求解车身骨架的耐撞性优化问题。为解决此类优化问题，本文中提出了“子区域CA 模型”（subdomain CA）的概念，构建了车身骨架的子区域CA模型，提出了求解车身骨架厚度优化的子区域混合元胞自动机（subdomain hybrid cellular automata for thickness optimization，SHCA-T）算法，同时提出基于SHCA-T 算法的多工况优化方法（简称“多工况SHCA-T”），用于高效求解含有大量厚度变量的车身骨架多工况耐撞性优化问题。主要创新性工作体现以下几点：（1）通过构建车身骨架的子区域CA 模型，将经典HCA 方法拓展应用于离散型设计空间的非线性动态结构优化问题；（2）内层循环提出阶跃式目标内能密度函数及其更新规则，以提高SHCA-T 和多工况SHCA-T 方法的全局搜索能力；（3）内层循环使用基于PID 控制策略的元胞厚度更新规则，以提高SHCA-T 和多工况SHCA-T 方法的稳健性；（4）寻优过程无须计算梯度信息，对于求解复杂非线性且很难获得灵敏度信息的优化问题具有较大优势。为验证SHCA-T 和多工况SHCA-T 算法的精度和效率，将其用于求解侧面碰撞和侧面柱碰工况下车身骨架的厚度优化问题，并与并行EGOPCEI 算法的优化结果进行对比。结果表明：在收敛精度相当的条件下，SHCA-T 和多工况SHCA-T 算法具有更高的全局搜索效率。

1 SHCA-T算法原理

为高效求解包含大量厚度变量的车身骨架耐撞性优化问题，本文中提出“子区域CA 模型”的概念，构建了车身骨架的子区域CA 模型，提出SHCA-T 算法，从而将经典HCA 方法拓展应用于离散型设计空间的非线性动态结构优化问题。SHCA-T 方法包括外层循环和内层循环。外层循环开展碰撞有限元仿真分析、计算输出响应，并更新目标质量，以实现结构质量最小化。为有效提高SHCA-T 方法的全局搜索能力和稳健性，在内层循环分别提出阶跃式目标内能密度函数及其更新规则和基于PID 控制策略的厚度更新规则；内层循环主要根据当前元胞及其邻胞的内能密度，按照PID 控制策略调整元胞厚度，使内层循环的当前质量收敛于目标质量；最终使元胞内能密度分布尽可能逼近目标内能密度函数，如图1所示。

图1 SHCA-T算法流程图

1.1 子区域元胞自动机（CA）模型的定义

以车身梁骨架的厚度优化为例，说明车身梁骨架子区域CA模型的定义过程。

步骤1-子区域划分：根据车身结构的拓扑连接特点，将设计域划分为若干个相互独立的子区域，记为Ωi。

步骤2-元胞定义：分别在子区域Ωi内，将每个部件定义为一个元胞（记为Ωi，j），Ωi，j的下标i表示第i个子区域的序号，下标j表示当前元胞在第i个子区域内的位置；在每个子区域Ωi(i=1，2，…，l)内，按照由内向外、从前到后、自下而上的原则，依次将元胞下标j从小到大编号。

步骤3-元胞状态变量定义：依次为元胞定义设计变量（如部件厚度）与场变量（如内能密度）。

步骤4-元胞邻域定义：遍历所有子区域Ωi(i=1，2，…，l)，将同一个子区域内的元胞，根据下标j的大小确定当前元胞的邻胞，当前元胞的邻胞集合称之为邻域。例如，图2 中定义了3 个子区域，令元胞半径r=1，以当前元胞为中心、以r为元胞半径范围内的所有元胞称为当前元胞的邻胞；在子区域Ω1内当前元胞Ω1，2的邻胞数量=2，在子区域Ω2内当前元胞Ω2，1的邻胞数量=1，在子区域Ω3内当前元胞Ω3，1的邻胞数量=1。

按照上述步骤，总共为车身梁骨架模型定义了14个子区域，如图2所示。

图2 车身骨架的子区域CA模型示意图

1.2 内层循环

1.2.1 阶跃式目标内能密度更新规则

以图2 中的车身骨架为例，说明阶跃式目标内能密度函数（step IED target，SIED*）的构造与更新规则。

步骤3-确定“阶跃点”和“阶跃区间”。遍历所有元胞，判断式（3）条件是否成立。若条件成立，则将的下标id定义为一个“阶跃点”，记为idi。假设根据式（3）确定了m个“阶跃点”，则这m个“阶跃点”可形成m+1 个“阶跃区间”，记为［idi-1，idi］，其中i=1，…，m+1，id0=1，idm+1=

步骤4-更新“阶跃点”和“阶跃区间”。令“阶跃区间”的宽度阈值为Hthreshold，遍历所有“阶跃区间”，判断式（4）条件是否成立。若式（4）成立（即“阶跃区间”［idi-1，idi］的宽度较窄），则按照如下方式删除“阶跃点”，并更新“阶跃区间”：当i=1时，删除“阶跃点”id1，“阶跃区间”由［id0，id1］更新为［id0，id2］；当i＞1时，删除“阶跃点”idi-1，“阶跃区间”由［idi-1，idi］更新为［idi-2，idi］。若式（4）不成立，则保留原“阶跃点”和“阶跃区间”。假设更新后的“阶跃点”数量为m'，则更新后的“阶跃区间”数量为m'+1。

步骤5-构造阶跃式目标内能密度函数，方程为

式中为第k次外循环、第h次内循环中“阶跃区间”［idi-1，idi］内的目标内能密度。

步骤6-更新阶跃式目标内能密度函数：为达到外层循环给定的目标质量，按照式（6）更新内循环中各“阶跃区间”的目标内能密度。

式中：M*(k)表示第k次外层循环更新得到的目标质量；M(h，k)表示第k次外循环、第h次内层循环由厚度更新得到的当前质量。当每次进入内层循环后每个“阶跃区间”的初始目标内能密度为

1.2.2 元胞厚度更新规则

基本的元胞厚度更新公式为

1.2.3 内层循环收敛准则

当内层循环的当前质量收敛于目标质量时，SHCA-T算法的内层循环达到收敛条件：

式中：ε1为质量收敛因子；k1为内层循环的迭代次数；k1max为内层循环的最大迭代次数。

1.3 外层循环

利用有限步长二分法实现目标质量的迭代更新［8］。当设计点为可行解时，外层循环降低目标质量；当为不可行解时，外层循环增加目标质量；直到相邻两个设计点出现一个为可行解、另外一个为不可行解时，有限步长二分法将在这两个设计点之间进行局部搜索。

1.4 全局收敛条件

SHCA-T算法包括以下3个收敛条件，只要满足任意一个条件，算法将收敛：

（1）外层循环的迭代次数k超过预先定义的最大迭代次数kmax；

（2）有限步长二分法连续出现“不可行解”的数量p＞

（3）设计变量的变化量非常小：

式中：N表示元胞总数；ε2表示全局收敛因子。

2 多工况SHCA-T算法

本文主要解决多工况下车身骨架的耐撞性与轻量化问题，该优化问题的数学方程为

式中：Mlc为第lc个工况的结构质量；glc(t)为第lc个工况的约束函数（如侵入量、侵入速度等）；ωlc为第lc个工况的权重系数；Nlc为工况数量；tmin为厚度变量矩阵的下限；tmax为厚度变量矩阵的上限。

为求解上述优化问题，在SHCA-T 算法的基础上，通过改进阶跃式目标内能密度和元胞厚度的更新规则，得到基于SHCA-T 算法的多工况优化方法（简称“多工况SHCA-T 算法”）。下面简要介绍多工况SHCA-T算法的改进之处。

（1）阶跃式目标内能密度更新规则

在多工况SHCA-T 算法中，各工况的阶跃式目标内能密度函数按照1.2.1 节进行独立更新，其数学表达式为

式（16）更新为

式中：M*(k)表示第k次外层循环更新得到的目标质量；M(h，k)表示第k次外循环、第h次内层循环由厚度更新得到的当前质量。

（2）元胞厚度更新规则

在多工况SHCA-T 算法中，元胞厚度按照式（9）更新，元胞厚度变化量按照式（18）更新，表达式为

3 车身骨架多工况耐撞性优化设计

分别按照GB 20071—2006《汽车侧面碰撞的乘员保护》和GBT 37337—2019《汽车侧面柱碰撞的乘员保护》法规要求，开展整车侧面碰撞和侧面柱碰仿真分析，如图3 所示，并利用SHCA-T 算法和多工况SHCA-T 算法开展不同工况下车身骨架的轻量化设计。本文使用的整车碰撞模型总质量为1 346 kg，包含276 838个单元、284 961个节点。

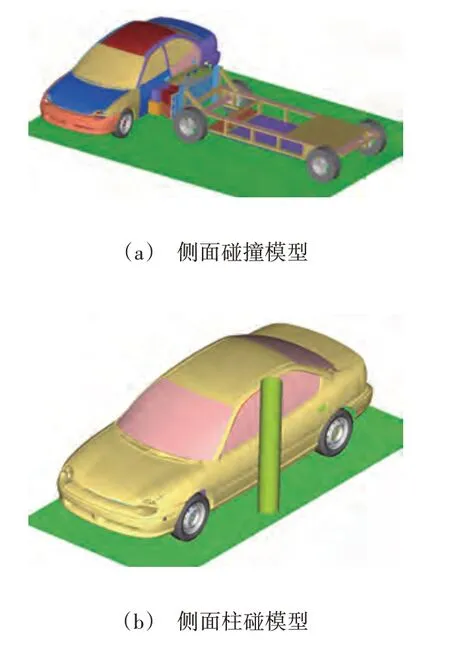
图3 侧面碰撞和侧面柱碰仿真模型

3.1 设计变量定义

针对侧面碰撞和侧面柱碰，定义A 柱、B 柱、门槛、上边梁、车门、前后纵梁、座椅横梁、顶盖横梁等34个零件的厚度为设计变量，如表1所示。

表1 车身骨架设计变量 mm

3.2 输出响应定义

选取B柱对应胸部和骨盆位置的最大侵入量、B柱对应胸部和骨盆位置的最大侵入速度作为侧面碰撞的输出响应，分别记为d1（x）、d2（x）、v1（x）、v2（x）；选择B 柱对应胸部和骨盆位置的最大侵入量、车门对应胸部和骨盆位置的最大侵入量作为侧面柱碰的输出响应，分别记为d3（x）、d4（x）、d5（x）、d6（x）。

3.3 优化方程定义

图4 为侧面碰撞与侧面柱碰的响应曲线对比。由图4 可知，初始设计的碰撞性能无法满足GB 20071—2006《汽车侧面碰撞的乘员保护》和GBT 37337—2019《汽车侧面柱碰撞的乘员保护》法规要求，为此本文定义了以下3种优化问题。

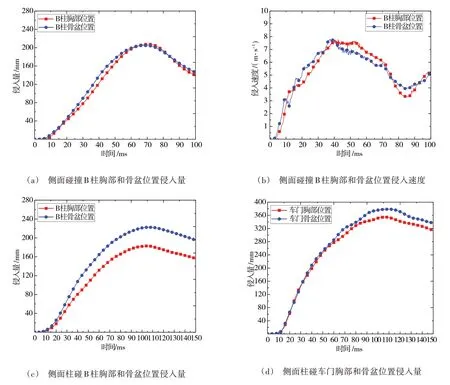
图4 侧面碰撞与侧面柱碰的输出响应曲线

（1）侧面碰撞工况下，车身骨架轻量化设计的优化方程为

（2）侧面柱碰工况下，车身骨架轻量化设计的优化方程为

（3）多工况（侧面碰撞与侧面柱碰）下车身骨架轻量化设计的优化方程为

式中ω1表示侧面碰撞工况的权重系数（本文取0.5），(1 -ω1)表示侧面柱碰工况的权重系数。

3.4 优化结果与讨论

选用并行EGO-PCEI 算法验证SHCA-T 算法和多工况SHCA-T 算法的优化效率。并行EGO-PCEI算法是一种基于伪CEI 准则并行加点的EGO 算法，对于求解耗时的约束优化问题具有较高优化效率，算法原理详见文献［3］。本文中，并行EGO-PCEI 算法的初始样本点数量设置为4，每次迭代基于伪CEI准则增加4个样本点（用于并行计算4个样本点的有限元响应值）。图5对比了侧面碰撞工况下SHCA-T算法和并行EGO-PCEI 算法的目标函数迭代历程曲线，图6 对比了侧面柱碰工况下SHCA-T 算法和并行EGO-PCEI 算法的目标函数迭代历程曲线，图7对比了侧面碰撞与侧面柱碰工况下多工况SHCA-T算法和并行EGO-PCEI 算法的目标函数迭代历程曲线。表2～表4 分别统计了上述3 种优化问题的优化结果、有限元分析次数和总计算时间。

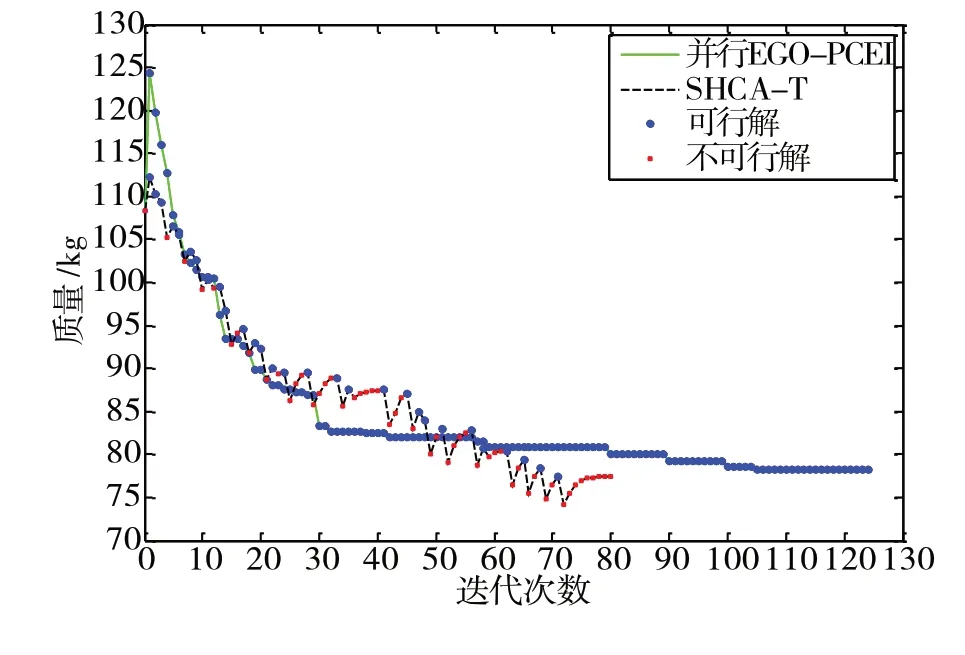
图5 侧面碰撞工况下目标函数迭代历程

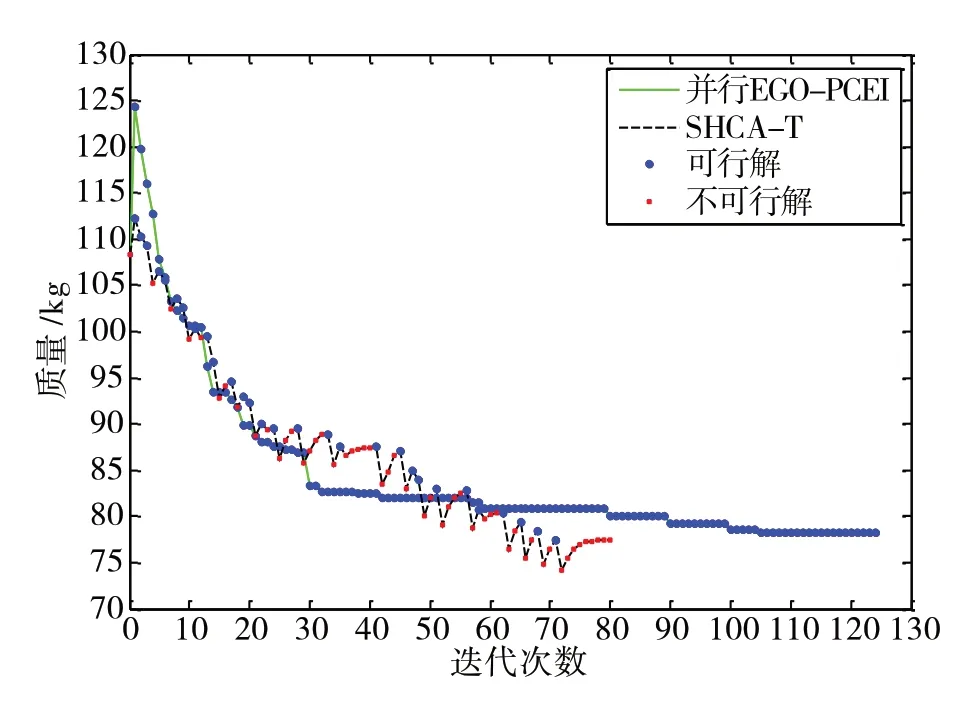
图6 侧面柱碰工况下目标函数迭代历程

图7 多工况下目标函数迭代历程

对比分析图5～图7和表2～表4可知：（1）SHCAT 和多工况SHCA-T 算法的全局搜索能力与并行EGO-PCEI 算法相当，且最优质量的误差控制在1%以内，原因是所提方法的内层循环引入了阶跃式目标内能密度函数及其更新规则和基于PID 控制策略的厚度更新规则，保证了所提算法的全局搜索能力和稳健性；（2）与并行EGO-PCEI 算法相比，SHCA-T和多工况SHCA-T 算法具有更高的全局优化效率，原因为所提方法是一种非梯度性的启发式算法，寻优过程无须计算梯度信息，主要通过内能密度更新规则和元胞厚度更新规则实现设计变量更新，具有较高的优化效率；（3）相比并行EGO-PCEI 算法，SHCA-T 算法分别节省了36%（侧面碰撞）和77.60%（侧面柱碰）的总计算时间；多工况SHCA-T算法在使用前者50%的计算资源情况下，节省了61.60%的总计算时间。由此可见，SHCA-T 和多工况SHCA-T 算法对于求解非常耗时的、多变量的非线性动态响应优化问题具有较高的寻优效率和精度，同时也验证了该算法的有效性。

表2 侧面碰撞工况下优化结果对比

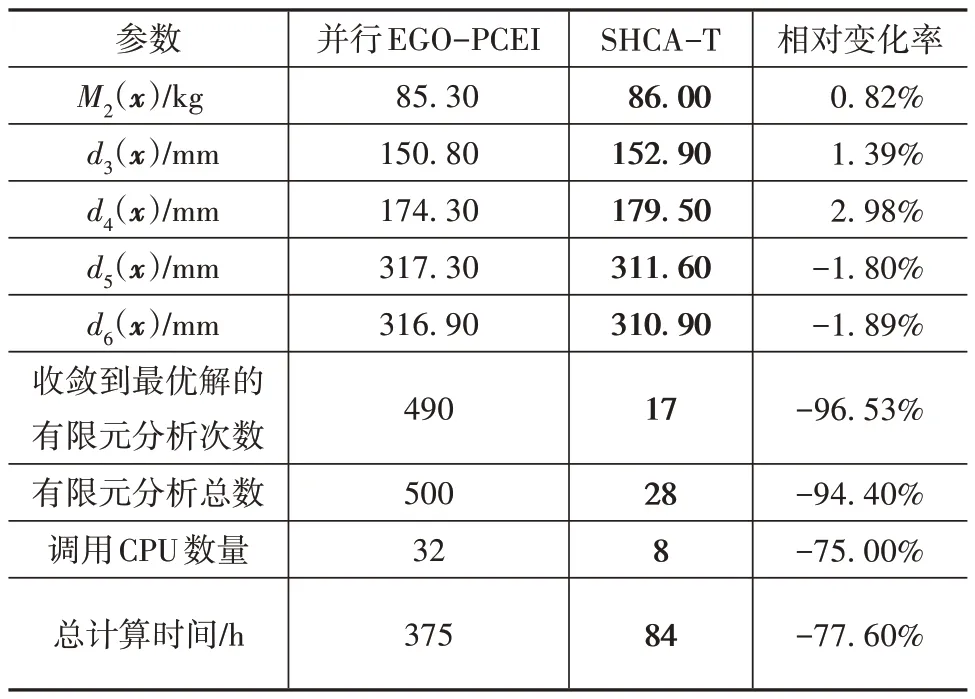
表3 侧面柱碰工况下优化结果对比

表4 侧面碰撞与侧面柱碰工况下优化结果对比

4 结论

为解决多变量非线性动态结构优化问题效率低的难题，本文中提出车身骨架厚度优化的子区域混合元胞自动机（SHCA-T）算法以及多工况SHCA-T算法，并用于求解侧面碰撞和侧面柱碰工况下车身骨架的厚度优化问题。主要结论概括如下。

（1）根据车身骨架的空间框架特点，提出了“子区域CA 模型”的概念，通过构建车身骨架的子区域CA 模型，将经典HCA 方法拓展应用于离散型设计空间的非线性动态结构优化问题。

（2）在内层循环提出阶跃式目标内能密度函数及其更新规则，提高了SHCA-T 和多工况SHCA-T算法的全局搜索能力。

（3）内层循环使用PID控制策略更新元胞厚度，提高了SHCA-T和多工况SHCA-T算法的鲁棒性。

（4）相比单工况优化，多工况优化问题的最优车身骨架的质量更大。