凸凹不平道路几何参数识别和模型重构方法研究*

伍文广，田双岳，张志勇，金 斌，邱增华

（1.长沙理工大学汽车与机械工程学院，长沙 410114；2.湘电重型装备有限公司，湘潭 411101）

前言

自动驾驶汽车能减少交通事故，提高通行效率，在民用、工业和国防等领域都有广泛的应用前景。工地矿山的生产运输、未知环境的探索开发和战场区域的侦查攻击等凸凹不平道路环境是自动驾驶汽车多类型、全路况应用的一个重要组成部分。但是，与铺装公路的路面参数和感知技术开展了大量研究形成鲜明对比的是，凸凹不平道路参数识别和模型重构方法的研究成果非常少，同时由于凹坑或凸起形状复杂不规律，传统的参数识别研究方法在此特殊工况下已不适应［1］。

通过加速度传感器测量簧下质量垂直加速度可获取路面不平度信息［2-4］，Liu等［5］提出了一种基于簧下质量加速度的半主动悬架道路轮廓在线估计方法，该方法通过加速度信息反求得到路面输入信息，采用功率谱估计方法得到路面功率谱实现路面粗糙度等级分类。Xue等［6-8］利用智能手机自带的加速度传感器测量车身加速度信号，识别路面轮廓并检测了路面坑洞，但由于车辆悬架系统通常具有非线性，因此这种方法精度不高。此外，寇发荣等［9］采用位移传感器测量簧载质量位移与非簧载质量位移来计算路面不平度，Kang 等［10］利用车轮行程、簧载质量与非簧载质量加速度，提出一种基于离散卡尔曼的路面不平度估计方法。但是凸凹不平道路具有多变性、复杂性的特点，对路面参数的提前感知具有更高要求，以上基于加速度传感器、位移传感器的路面参数反向辨识方法，虽能对路面粗糙度、轮廓、道路病害位置进行判断，但不能满足自动驾驶汽车凸凹不平道路环境下对路面几何参数感知前瞻性的需求。

图像识别方法能较好实现路面参数的提前感知，图像直方图能直观地表示每个灰度值下的像素数，对于视差较为明显的图像能有较好的识别效果［11-12］。Wang 等［13］通过构造路面图像的小波能量场，基于形态学处理和几何判据对路面坑洞进行检测，将灰度和纹理信息有效结合，但效率较低。为此，支持向量机（SVM）被应用于路面特征检测［14］，虽然该方法优于传统方法，但对于多类别数据的分类具有局限性，卷积神经网络（CNN）能将图像数据直接输入神经网络，不需要复杂的图像预处理，具有较强的背景滤波能力［15-20］，因此被广泛应用于路面参数识别。但由于凸凹不平道路环境下路面特征的视觉信息不明显（如图1 所示），加大了图像识别的难度，且凸凹不平道路夜间光照条件恶劣，可能导致图像识别算法失效，此外，图像的二维特性使得图像识别难以准确提取路面三维参数。

图1 凸凹不平道路的典型特征

Zhao 等［21-23］通过激光雷达和其它辅助传感器获取路面粗糙度信息。Lee 等［24］在获取路面粗糙度信息的同时，通过设置平均距离的阈值来识别路面的凹凸物。Zhang 等［25］基于包络线和变形支撑点构建的剖面标准轮廓获取路面变形信息，并根据设定的深度阈值对沥青路面的裂缝和变形缺陷进行分类识别。刘家银等［26］设计了一种具有互补能力的多激光雷达安装方式，并通过距离阈值与点密度阈值对凹坑进行识别。Feng等［27］分析了以高度变化、高度差、数据点与拟合曲面之间距离、粗糙度值等特征为阈值的多种沥青路面裂缝检测算法，证明了基于阈值方法的可靠性。受Pointnet/Pointnet++的启发［28-29］，出现了许多基于点云的深度学习方法，可以更好地完成3D 模型分类、场景语义分割等任务，但它依赖于大量的点云数据进行学习。现有的点云公开数据集主要基于城市道路场景［30］，目前尚无凸凹不平道路场景的公共数据集。

总之，针对凸凹不平道路场景，反向识别方法的前瞻性不够；基于图像的方法难以准确获取路面特征三维信息且受环境光线影响较大；相比之下，激光雷达有效探测距离能达到数10 m，有较优的前瞻性，受环境光线变化小且能方便准确地获取路面三维信息，但由于缺乏凸凹不平道路场景下的数据集，难以通过深度学习方法对道路进行语义分割。为解决凸凹不平道路场景下的道路特征识别问题，本文中提出一种基于斜率阈值分割的道路特征识别和模型重构方法，不依赖于大量数据集的学习，通过分析路面特征的斜率进行参数识别，具有实现简单、时间成本低、计算量小的特点。

1 总体框架

本文中提出的凸凹不平道路典型特征（图1）参数识别和模型重构方法总体框架如图2 所示，主要分为3 个模块：（1）点云平滑模块，通过坐标系转换、Lowess 平滑等方法对原始数据进行转换和平滑，提高了数据精度，减少了计算量；（2）特征识别与提取模块，通过斜率阈值分割算法，对路面凸起、凹坑等典型特征进行识别分割；（3）参数拟合和模型重构模块，通过不同特征的边界点构建分段多项式函数，再基于带约束的分段函数拟合方法对路面点云数据进行函数重构。

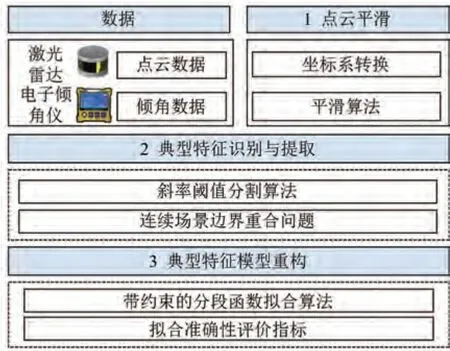
图2 凸凹不平道路几何参数识别和模型重构方法框架

2 点云平滑

激光雷达工作时振动、环境干扰等因素导致点云数据粗糙，影响识别和建模的精度与速度。对此，本文中提出一种点云平滑模型，首先，对原始点云数据进行坐标系转换，将点云坐标还原至水平，并采用直通滤波算法对道路点云进行提取，最后，基于Lowess平滑算法对点云进行平滑。

2.1 坐标系转换

如图3 所示，激光雷达的水平安装能扫描更远的范围，但对路面信息的获取有限，扫描到路面凹坑的数据少且稀疏；倾斜安装可将全部扫描线扫描至路面，提高激光雷达数据的利用率，尽管倾斜安装降低了扫描距离，但扫描范围更集中，扫描到路面凹坑的数据多且密集。因此，针对路面识别场景，将激光雷达以一定角度倾斜安装，能采集更密集的点云数据，但是，点云坐标系也随之发生变化，通过三维刚体几何变换方法将点云坐标转换至激光雷达水平状态下的坐标系，如式（1）所示。

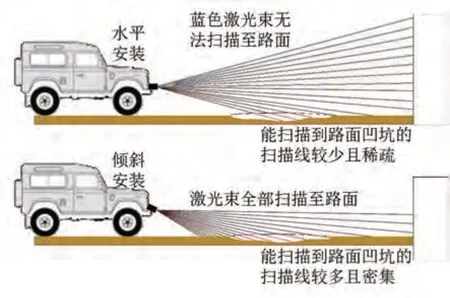
图3 激光雷达安装方式对比

激光雷达扫描的点云包括道路和环境信息，本研究主要针对道路特征的识别和建模，为降低干扰，减少计算量并提高准确性，对道路点云数据通过直通滤波方法进行提取。根据点云的属性（如坐标、颜色值等），对点云进行滤波，保留指定范围内的点云。

2.2 基于Lowess的点云平滑方法

Lowess方法中损失函数定义为

式中：xi、yi、zi为局部区域内的一点Ti(xi，yi，zi)的坐标值；K为局部区域内数据点个数；w1(i)、w2(i)分别为X-Y平面、X-Z平面下权值；P(xi)、Q(xi)分别为X-Y平面、X-Z平面的线性回归函数。

将式（3）代入式（2）并转换为矩阵形式：

权值函数w1，2(ri)选择三次函数：

式中：ξ(xξ，yξ，zξ)为选定局部区域中心点；ri为点Ti与点ξ在X-Y平面或X-Z平面欧式距离。

将式（7）值代入式（3）即可求得该局部区域内的回归中心(xi，P(xi)，Q(xi))。图4 为点云平滑前后点云数据的对比，从其中一扫描线平滑前后在X-Z平面的局部放大图可知：平滑前相邻点间有阶跃性的变化，数据噪声较大；平滑后点云数据连续光滑，能较好体现路面特征形状的变化趋势。

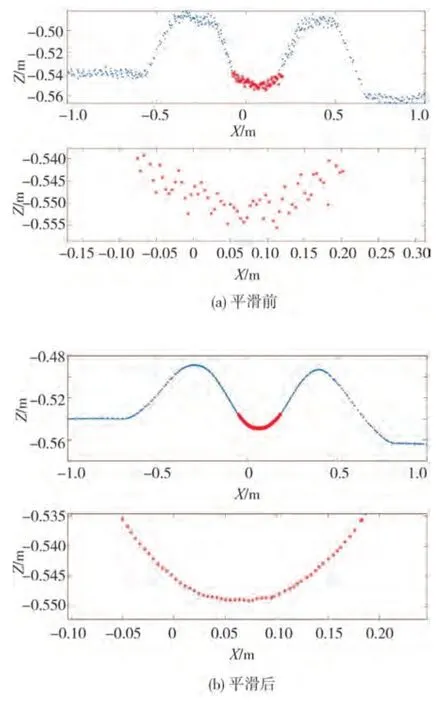
图4 点云平滑前后点云数据对比

3 路面典型特征识别与提取

3.1 基于斜率阈值分割的路面典型特征提取

为准确判断路面凹坑或凸起的起始和结束位置，本文中提出了基于斜率阈值分割的路面典型特征提取方法。基本原理为：根据各特征的扫描线斜率趋势，基于所设定的斜率阈值确定这些特征的坐标范围。如图5所示，凸起特征扫描线在X-Z面上投影特征表现为先上升再下降的趋势，对应于斜率图上其特征表现为起点开始于第一次大于最大斜率阈值Kmax的点，结束于离起点最近、最后一次小于最小斜率阈值Kmin的点。对于凹坑特征扫描线在X-Z平面的投影特征表现为先下降再上升的趋势，对应于斜率图上其特征表现为起点开始于第一次小于最小斜率阈值Kmin的点，结束于离起点最近、最后一次大于最大斜率阈值Kmax的点。

图5 点云投影和斜率计算

取平滑后点云数据投影至X-Z平面，计算相邻点(xi，zi)、(xi+1，zi+1)、…、(xi+2m，zi+2m)的斜率ki，如式（8）所示。

式中m取值为正整数，2m值为所取数据段长度，m值越大，斜率值越光滑，但同时会导致斜率偏差增大。

通过式（8），得到的斜率数据量仅有原点云数据量的1/2m，导致部分点云数据点无对应斜率值。针对此，采用线性插值方法将计算的斜率值数据量还原至与点云数据量相同，使每个点云数据对应其斜率值。

为避免重复数据检索，在进行典型特征识别检索时对检索区域进行不断更新，将已检索区域排除在后续检索区域范围外。如图6 所示，将点云数据以X值为基准进行升序排列，检索最开始将整个扫描线点云数据设定为检索区域1，并从较小的X值开始检索，当检索识别到第1 个典型特征凹坑1时，以凹坑1 终点的X坐标为边界，与扫描方向相反一侧为已检索区域，后续不再检索，与扫描方向相同一侧更新为检索区域2，同理，当检索到第2 个典型特征时，检索区域更新至区域3，以此类推，直至没有检索到典型特征为止。

图6 典型特征检索方法

图7 为典型特征判定流程图，其中：ki为点云数据点xi对应的斜率值；Kmin和Kmax为设定的最小和最大斜率阈值；σ为防止小范围斜率波动引起特征终点判定提前终止的误差因子，其值为正整数；num为记录达到终点停止更新判定次数的计数器，初始值为0。

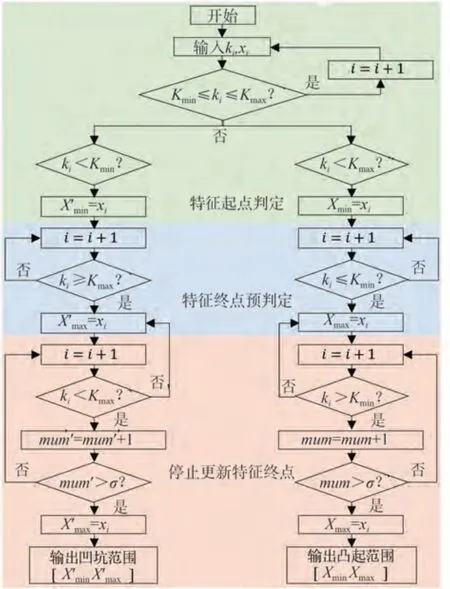
图7 典型特征判定流程

典型特征的判定主要可分为如下3个步骤。

第1 步为起点判定，依次检索扫描线斜率数据ki，当斜率ki在斜率阈值范围内(Kmin≤ki≤Kmax)，认为此时路面为正常平缓路面，当斜率ki小于kmin（ki≤kmin）或大于Kmax时，判定该点为凹坑起点(X'min=xi)或凸起起点(Xmin=xi)。

第2 步为终点预判定，从检索到特征起点开始，终点判定开始运行，对于凹坑终点判定，当检索到斜率大于Kmax（ki≥Kmax）时，终点更新至当前检索位置(X'max=xi)；对于凸起终点判定，当检索到斜率小于Kmin(Ki＜Kmin)时，终点更新至当前检索位置(Xmax=xi)。

第3 步为特征终点停止更新判定，从检索到特征终点开始，终点停止更新判定开始运行，对于凹坑或凸起终点停止更新判定，每当检索到斜率小于Kmax（ki＜Kmax）或斜率大于kmin(ki＞Kmin)时，计数器加1(num'=num'+1) 或(num=num+1)，当计数值大于σ(num' ＞σ或num＞σ)时，确定最终的凹坑或凸起终点(X'max=xi或Xmax=xi)，并输出凹坑或凸起特征点云范围([X'minX'max]或[XminXmax])。

3.2 凸起与凹坑连续场景下边界重合问题

实际情况中路面凸起与凹坑通常存在连续边界，典型特征提取中凸起终点的判定为最后一个斜率小于斜率阈值Kmin的点，而凹坑起点的判定为第一个斜率小于斜率阈值Kmin的点，两者范围存在重合，同理，还存在凹坑终点与凸起起点重合现象。针对此，对连续场景下的边界进行重新判定，依次检索每条扫描线中的凸起点云范围与凹坑点云范围，判断凸起起点或终点是否在凹坑点云范围内，判断成立时说明凸起与凹坑范围重合，令重合范围的中点作为新的范围边界，最终实现的效果如图8所示。

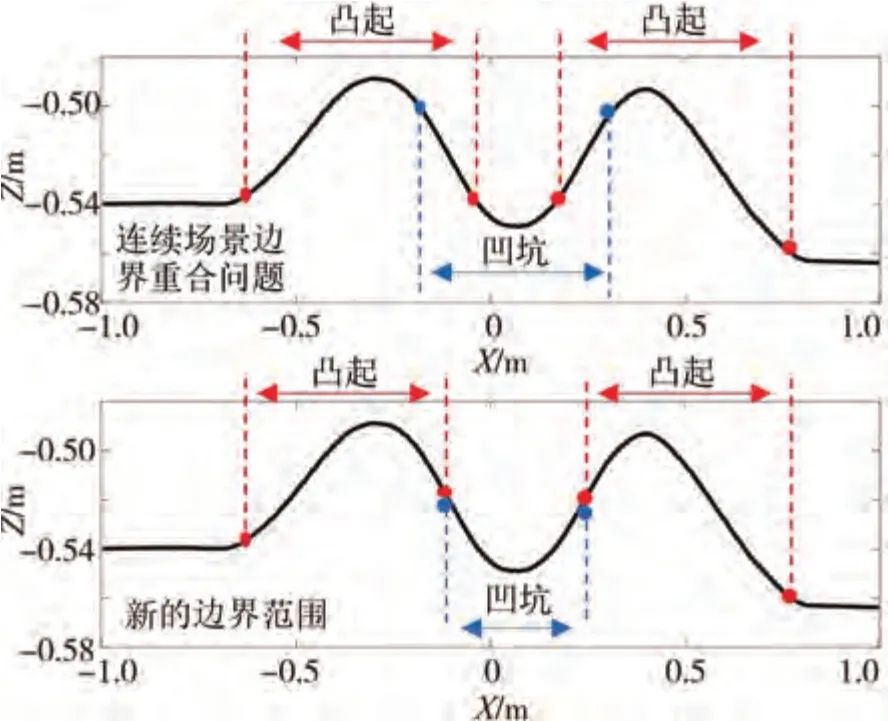
图8 连续场景下边界范围

4 典型特征数学模型重构

连续的凹坑或凸起导致曲线形状复杂，分段拟合方法可提高精度、降低拟合函数次数。如图9 所示，在车辆前方区域进行路面扫描，Y轴方向为车辆前进方向，X轴为车辆横向方向。以其中一条扫描线为例，通过典型特征识别与提取方法，得到各个典型特征点云在X轴方向上的边界值，以这些边界值为节点，通过多项式对各个分段进行拟合，得到拟合后的扫描线函数。

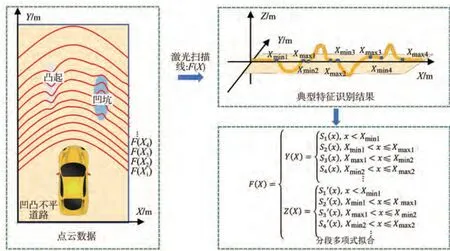
图9 凸凹不平道路数学模型重构方法

4.1 带约束的分段函数拟合方法

分段函数拟合时在分段点处会出现不连续的阶跃现象，为提高分段点处光滑性，采用带约束的分段拟合方法。

式中：Si(x)为多项式函数；a0i，a1i，…，a(n-1)i，ani为待定系数；n为多项式次数。

在分段点处添加一个约束条件，使节点处函数值相等，如式（11）所示。

式中x-、x+为节点处点云X坐标值。

4.2 拟合结果评价

设(xi，yi，zi)为原始点云坐标，(xi，yi'，zi')为拟合后的点云坐标值，其中yi'、zi'通过式（9）计算得出，以点云坐标的均方根误差作为拟合效果的评价指标，如式（12）所示。

式中：RMSE为均方根误差值；N为点云数据点数量。

5 实验验证

5.1 数据描述

为验证上述方法的可行性，在实验室场景下搭建了4种典型特征场景，扫描了3种典型凸凹不平路面，如图10 所示。其中场景1 模拟路面存在一个凸起中间一个凹坑；场景2 模拟路面横向方向存在两个凸起；场景3 模拟路面横向方向存在两个凹坑与一个凸起；场景4 模拟路面一个凹坑；场景5 模拟路面一个凸起；场景6 模拟路面纵向方向存在两个凹坑；场景7 模拟路面纵向方向存在两个凸起。采用VLP-16激光雷达获取点云数据，电子倾角仪获取激光雷达姿态角，其中激光雷达和电子倾角仪的技术参数如表1所示。

图10 实验场景

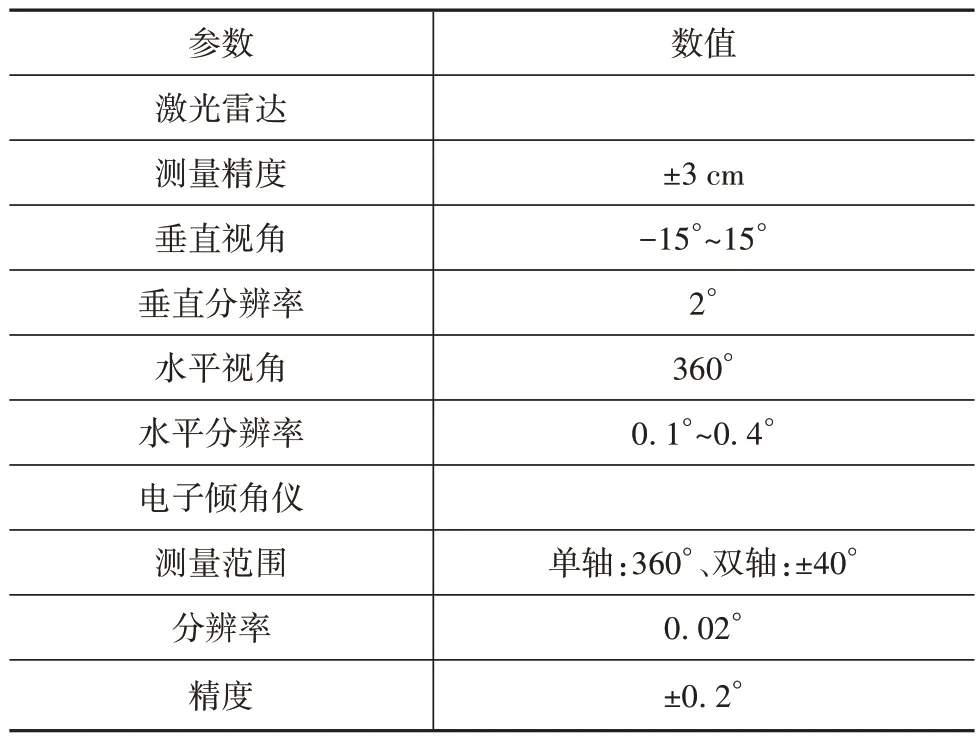
表1 激光雷达和电子倾角仪的技术参数

5.2 结果分析

5.2.1 变量取值

本研究中各个步骤中的变量取值如表2 所示。雷达倾斜角取值与雷达的安装高度和型号有关，本文通过理论分析和实验结果，雷达倾斜角α取值在23°～27°中较为合适，倾斜角β与θ值应尽可能的小。点云平滑时局部数据点个数K取值范围30～50，K值过大时，数据失真加剧，K值过小会导致曲线平滑质量降低。斜率计算时m值会影响斜率准确性，m值越大能更好反映斜率曲线变化趋势但准确性降低，m值越小斜率计算结果越准确但会放大噪声。斜率阈值[Kmin，Kmax]的选择影响典型特征提取效果，当阈值绝对值越大，坡度较缓的凹坑或凸起会被过滤。误差因子σ影响特征终点判定对斜率变化的敏感性。

表2 变量取值

5.2.2 路面典型特征识别与提取结果

通过路面典型特征识别与提取得到如图11 所示的典型特征提取结果，图上方为原始点云数据，下方为典型特征识别与提取后点云数据，其中：蓝色部分点云为非典型特征点云数据；黄色部分点云为凸起特征点云数据；红色部分点云为凹坑特征数据。

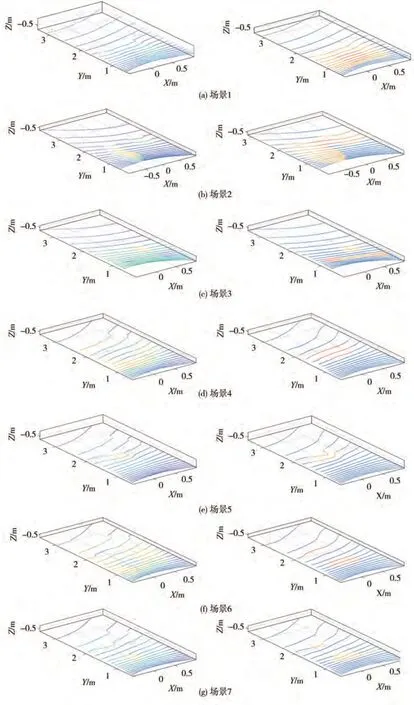
图11 典型特征提取

从结果可以看出，路面典型特征识别与提取后点云数据通过点云平滑处理后点云轮廓更为清晰，在各个场景下能基本准确识别特征类别与范围。如场景1 下能准确识别出路面存在的典型特征，能将两凸起中的凹坑特征进行识别且在凸起与凹坑连接处能有清晰的边界。但由于激光雷达线数的限制，在较远处点云数据变的稀疏，使得路面信息丢失。如场景5、场景7 凸起的背面以及场景6 在较远处的凹槽底部激光雷达无法扫描到，虽然本文算法能识别到路面存在凸起或凹坑，但信息较少无法对特征范围进行准确判断。相比之下，在较近处的点云数据较为密集，相邻激光扫描线之间的距离较近，能较好地对路面特征类别以及范围进行识别。

5.2.3 路面典型特征拟合结果

基于典型特征识别与提取结果，通过带约束的分段多项式拟合方法对点云数据进行拟合，如图12所示，其中各上方为不同场景下路面拟合结果，下方为曲面渲染后路面模型，从结果可以看出通过对分段点添加约束，使得拟合后点云在分段点处光滑性较好且未出现阶跃现象。

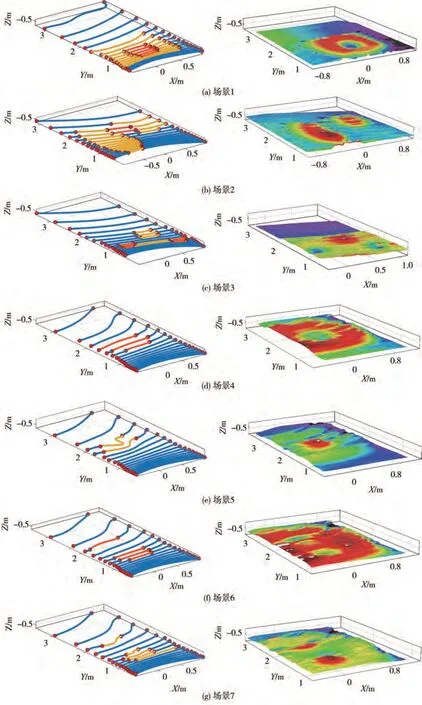
图12 典型特征拟合

5.3 拟合结果准确性分析

通过式（12）将各个场景下带约束分段多项式拟合数据、非分段多项式拟合数据与原始点云数据进行均方根误差比较。如图13 所示，在各个场景中，两种方法的拟合次数越高，RMSE 值越小，拟合准确性越好。不同的是，分段拟合方法在多项式次数达到5或6次时，拟合次数的增加对拟合准确性的提升幅度明显减小，此结果说明此时已经接近多项式函数拟合效果的极限，而分段拟合能在较低的拟合次数便达到拟合效果的极限位置。同时，在同一拟合次数下，分段拟合的不同场景RMSE 值的分布较为集中，而非分段拟合RMSE 值在拟合次数为2～7 的分布都较为分散，此结果说明，分段拟合对于不同场景的适应性更好，有较好的鲁棒性。

图14 展示了分段拟合与非分段拟合在各个场景不同拟合次数下RMSE 在0～0.015 m、0.015～0.030 m 和＞0.030 m 3 个分段内的分布情况。从结果可以看出，随着拟合次数的增加，RMSE 在0～0.015 m 的比例也随之增加，最终分段拟合方法保持在92%左右，而非分段拟合方法只能达到88%左右，此结果说明，分段拟合在拟合精度上比非分段拟合更具优势。同时，与图13 相对应的是，分段拟合在拟合次数达到5 或6 次时，RMSE 在0～0.015 m 的比例便基本达到最大值；而非分段拟合直到拟合次数达到8或9次时才达到最大值，进一步证明分段拟合能有效减少拟合次数，降低计算量。总的来说，分段拟合方法十分适合对凸凹不平道路路面模型进行数学重构，分段的特性能保证函数能适应凸凹不平路面多变的地形，同时较低的拟合次数能避免多项式函数复杂化。结合实验结果，将分段多项式拟合方法拟合次数设置为5 是最佳选择，一方面能保证较高的拟合精度，另一方面能减小计算量。

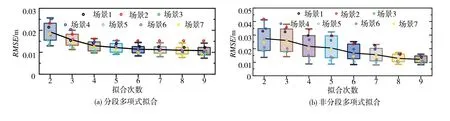
图13 各场景下拟合结果均方根误差

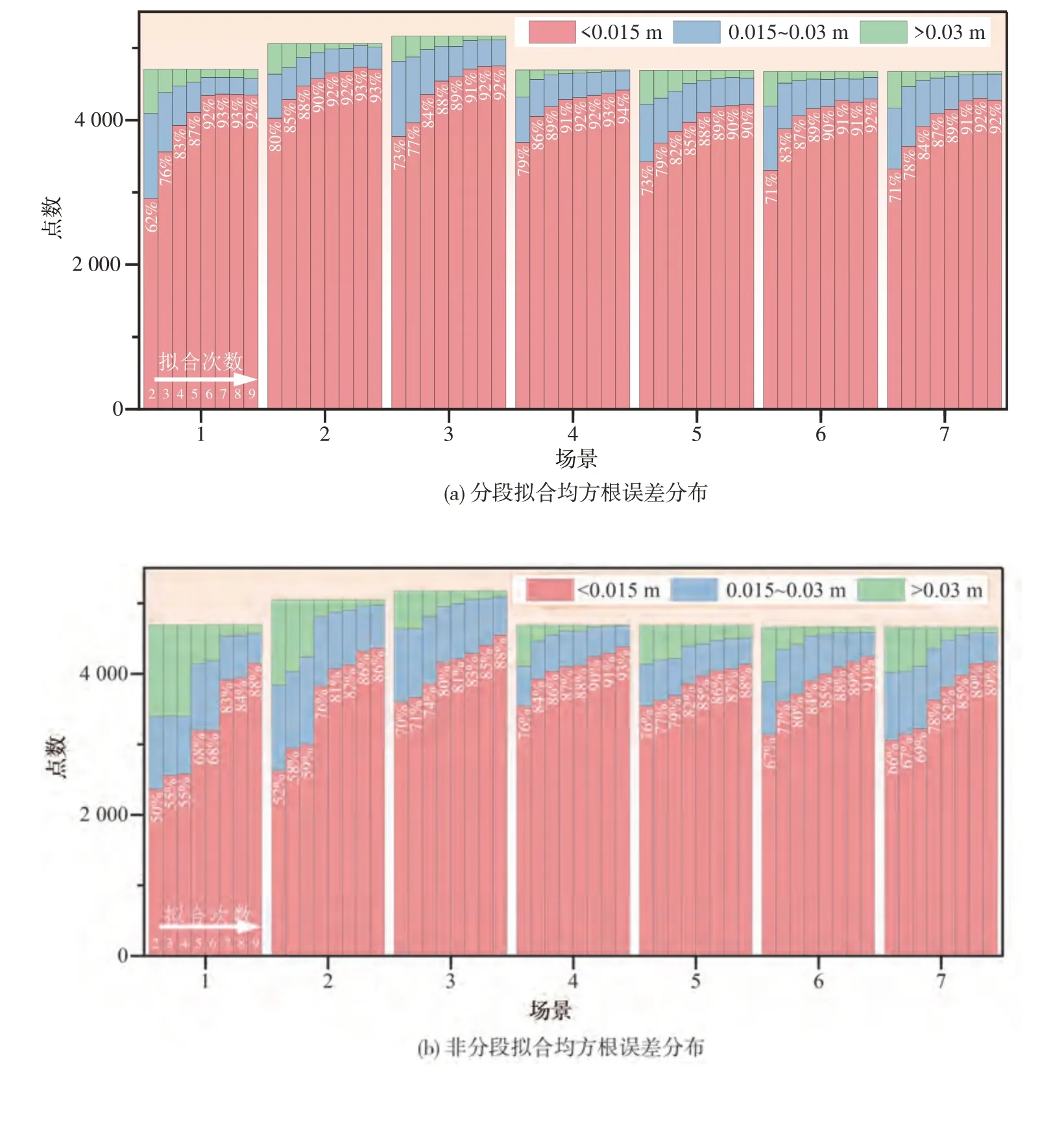
图14 各场景下拟合结果均方根误差分布

6 结论

本文中提出了一种基于激光雷达数据的凸凹不平道路典型特征几何参数识别和模型重构方法，研究成果有助于对凸凹不平道路进行识别感知，完善凸凹不平道路模型的参数化表达，从而为自动驾驶汽车路径规划、决策和控制提供路面数据参考。相比于现有的研究，本文主要贡献有如下3点。

（1）提出的典型特征识别和模型重构方法弥补了现有路面参数识别方法在凸凹不平道路应用性差的缺陷。

（2）提出了基于斜率阈值的典型特征提取方法，实现凸凹不平道路场景下对路面凹坑和凸起特征的提取与参数识别。

（3）本文提出并对基于带约束的分段多项式和非分段多项式拟合的路面参数模型重构方法进行了对比，结果表明，分段拟合方法具有较高的拟合精度和速度，能更好适应凸凹不平道路场景。