实车数据驱动的锂电池剩余使用寿命预测方法研究*

兰凤崇，陈继开，陈吉清，蒋心平，李子涵，潘 威

（1.华南理工大学机械与汽车工程学院，广州 510641；2.华南理工大学，广东省汽车工程重点实验室，广州 510641）

前言

随着锂电池技术的发展，锂电池的应用越来越广泛，锂电池的安全问题也成为研究焦点。陈吉清等［1］研究了不同滥用条件下车用锂电池安全性。黄芦等［2］研究了电动汽车电池包底部锥状物冲击下的力学响应。对于电动汽车而言，准确评估锂离子动力电池的健康状态（SOH）和预测锂电池的剩余使用寿命（RUL）在锂电池健康管理中起十分重要的作用。基于数据驱动的锂电池剩余寿命预测方法，无需了解电池失效的准确物理化学机理参数，可直接从锂电池的电压和电流等数据中挖掘出锂电池性能退化的规律，具有较强的适用性，逐渐成为近年来主流的锂电池剩余寿命预测方法。

Long 等［3］提出一种基于AR 模型的锂离子电池RUL 预测方法。Zhou 等［4］将ARIMA 模型用于锂电池的 RUL 预测中，结合经验模式分解（EMD）将全局退化趋势和SOH分离，从而得到RUL和SOH。Wang等［5］在不确定的条件下使用相关向量机（RVM）进行了锂电池剩余寿命预测，机器学习模型的重点在于核函数的选择和模型超参数的优化。张朝龙等［6］提出集合经验模态分解和多核相关向量机的方法，将锂电池衰退曲线分解后，进行锂电池剩余寿命预测。刘月峰等［7］提出一种融合多个核函数构建相关向量机预测模型的方法，通过果蝇算法优化多个核函数优化组合的线性方程系数，提高了预测模型的预测性能。

近年来，深度学习和神经网络模型的自适应特征学习能力，已在多个领域得到了成功应用。张瑞等［8］利用纯电动车企业20 台试验车辆的25 万条数据，引入深度学习中的循环神经网络（RNN）算法，并实现了电池数据管理的可视化、电池异常监控和预警功能。李向南［9］使用深度长短时记忆（LSTM）神经网络对锂电池剩余使用寿命进行预测，并开发了相关预测软件。

为提高模型的泛化能力，融合不同模型的方法得到应用，Liu 等［10］使用支持向量回归（SVR）与多层感知机（MLP）的融合方法预测了锂电池的剩余寿命，张吉宣等［11］提出了一种正则化粒子滤波和自回归移动平均模型相融合的锂电池剩余寿命预测算法，以锂电池的经验退化模型作为融合算法的状态方程，自回归滑动平均模型的预测输出值替代观测值，构建状态空间模型，迭代更新电池容量，实现锂电池的剩余使用寿命预测，胡天中等［12］提出基于多尺度分解和深度神经网络的电池 RUL 预测模型，用深度置信网络（DBN）模型和 LSTM 模型分别进行预测后融合。

基于统计学模型的时间序列预测方法具备预测长序列的能力，但模型对非线性较强的实车锂电池SOH 衰退趋势预测精度较低；基于深度学习的锂电池剩余使用寿命预测模型大多是针对锂电池SOH退化序列的单步预测建立的，此类模型的优点是短期预测的精度较高，但对较长序列进行预测时，须不断迭代地进行单步预测，直至预测终点，整个过程的预测次数越多，产生的累积误差就越大。因此，迫切需要找到更合适的通用方法，解决基于复杂实车数据情况下更加精确可靠的预测问题。

综上所述，在深度学习方法的基础上，分析国家标准GB/T 32960［13］所要求的企业车辆电池数据采集规范。尝试将编码器-解码器（ED）框架应用于对LSTM 模型的改进，并融合ARIMA 模型方法进行误差修正，形成ARIMA-EDLSTM 融合模型的锂离子动力电池RUL 预测方法。通过实例车型数据预测，表明该方法可靠，并具有精度方面的明显优势。

1 ARIMA-EDLSTM 融合模型方法

1.1 ARIMA模型原理

电池RUL 预测属于时间序列预测问题。ARIMA 模型是用于时间序列分析和预测的线性模型。使用ARIMA 进行分析预测时须设置3 个参数，分别为自回归阶数p、差分阶数d和移动平均阶数q，ARIMA（p，d，q）模型先对时间序列进行平稳性检验，如果不满足平稳性的要求，对时间序列进行d阶差分，然后再对序列进行建模。ARIMA（p，d，q）的一般形式如下：

式中：Xt为序列当前时刻值；Xt-j（j=1，2，…，p）是过去p个时刻的序列值；φi（i=1，2，…，p）表示各阶自回归项系数；μt为残差；θi（i=1，2，…，q）表示回归系数。

ARIMA 模型的建模过程一般分4个步骤：

（1）序列平稳化处理 一般可通过观察法观测时间序列样本的平稳性，若为非平稳序列，进行d阶差分运算，化为平稳时间序列。

（2）模型定阶 通过观察样本的自相关系数图和偏自相关系数图来选取参数p和q。一般以自相关系数图和偏自相关系数图中各自结尾的位置作为p和q的最大值，得到多种参数组合，再利用 AIC 信息量准则从中选择一组最优的模型参数。

（3）模型检验由以上得到的d、q、p获得ARIMA 模型，通过检验模型残差是否为白噪声序列来验证模型有效性。

（4）预测 根据历史序列数据对未来时刻值进行预测。

1.2 LSTM 模型原理

LSTM 是在RNN 的基础上进行改进的算法，能有效地学习时间序列数据中的特征，解决了RNN 训练过程中存在的梯度爆炸和梯度消失的问题，能够学习长期依赖信息。在RNN 的基础上，LSTM 增加了细胞单元的概念，细胞内部结构由输入门、遗忘门和输出门等组成。门结构用于控制长期信息的储存和丢弃。其中，输入门旨在确定保留在存储器单元中的新输入信息，遗忘门用来消除无用的过去单元状态，输出门用来确定传播到下一个存储单元的最终状态。LSTM 基本结构如图1所示。

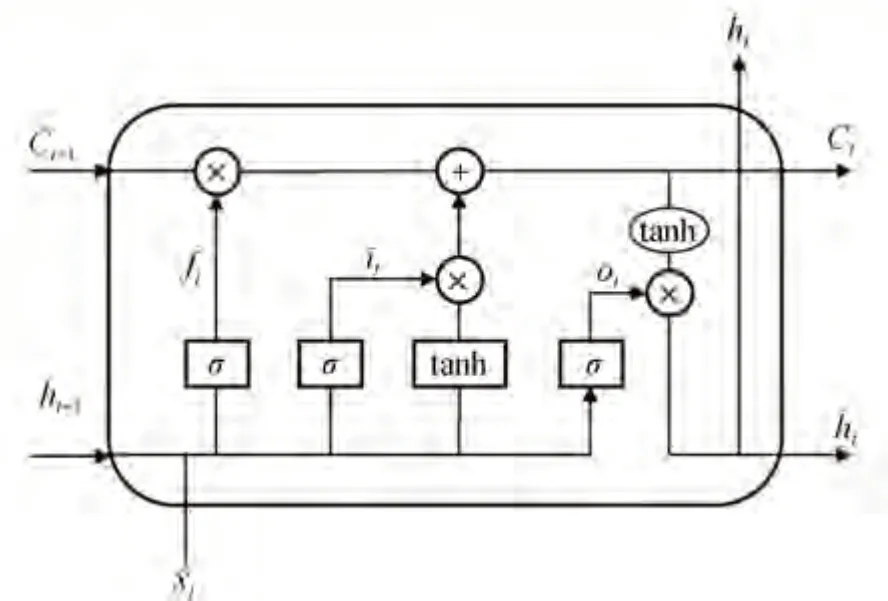
图1 LSTM结构

LSTM 的工作原理可以用式（2）～式（7）来表示：

式中：ft、it、Ot分别为遗忘门、输入门和输出门各自经过sigmoid 函数的输出，它们的值介于0 和1 之间，控制旧单元状态Ct-1中要遗忘的信息、当前单元状态中新增的信息C͂t和细胞单元t时刻的输出ht；xt为当前时刻的单元输入；ht-1和ht分别为上一时刻和当前时刻细胞单元的输出；Wf、Wi、Wc和Wo是对于输入xt的权重；bf、bi、bc和bo是相应的偏置。

使用单步LSTM 模型进行多步预测时，须把当前时刻预测值作为下一次预测的输入，不断迭代直至预测终点。图2 为单步LSTM 模型迭代预测k次的示意图。

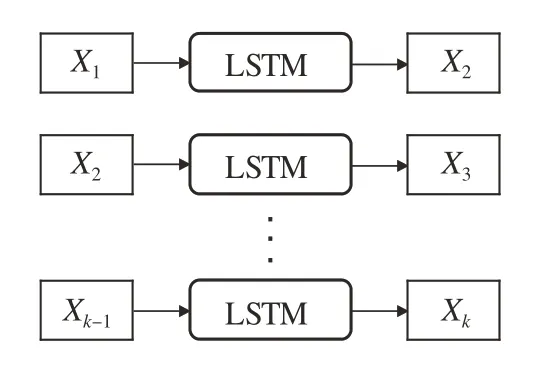
图2 单步LSTM模型迭代预测

1.3 EDLSTM 模型的构建

序列到序列的预测可以有效减少总的预测次数，以此减小误差随着预测次数的累积，ED 结构是一种序列到序列的预测结构，可以减少预测次数。已经有人将ED 框架与LSTM 组合用于交通流的预测中［14］，很好地解决了序列到序列的预测问题，收到了良好的效果。编码器将历史的序列信息压缩为一个固定维度的状态向量C，解码器对向量C进行解析，转化成输出序列，通过递归方式将预测结果反馈到网络中。ED结构如图3所示。

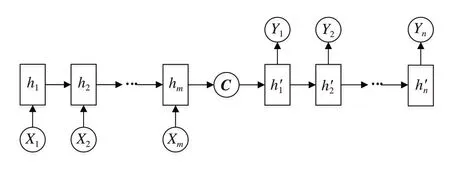
图3 Encoder-Decoder结构

对于ED 结构，须选择合适的编码器和解码器，LSTM可以学习序列中的长期依赖信息，对序列中每个数据的信息都能进行提取，所以选择LSTM 作为编码器和解码器，构建EDLSTM模型。

EDLSTM 模型的预测过程如图4 所示。在编码时，作为编码器的LSTM 模型对输入长度为m的序列进行特征提取，将输入的序列信息压缩为一个固定维度的状态向量CT。在m时刻，编码器的状态hm由当前输入xm以及前一时刻状态hm-1共同决定，状态向量CT是对输入序列所有状态的加权平均。

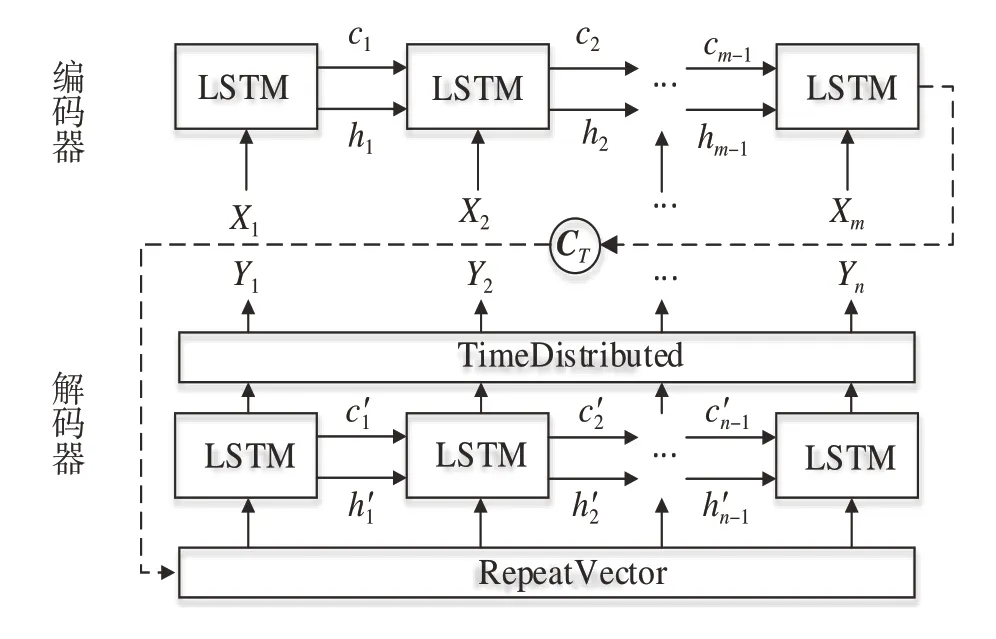
图4 EDLSTM模型预测过程

EDLSTM 模型在解码时，将状态向量CT通过RepeatVector 层作为解码器的输入，LSTM 模型的每个时间步的输出通过TimeDistributed 层得到最终的预测结果，完成状态向量的解码，将状态向量转换为长度为n的输出序列。

EDLSTM 模型可以实现序列到序列的预测，对于锂电池剩余寿命预测，EDLSTM 模型输入特征为序列长度为m的历史时刻的SOH值，输出为序列长度为n的未来时刻的SOH 值。图5 为输入序列长度为m、输出序列长度为n（m＞n）的EDLSTM 模型迭代预测k次的示意图。可见对于预测相同序列长度的数据，EDLSTM 模型相较于单步LSTM 模型可以明显减少预测次数。

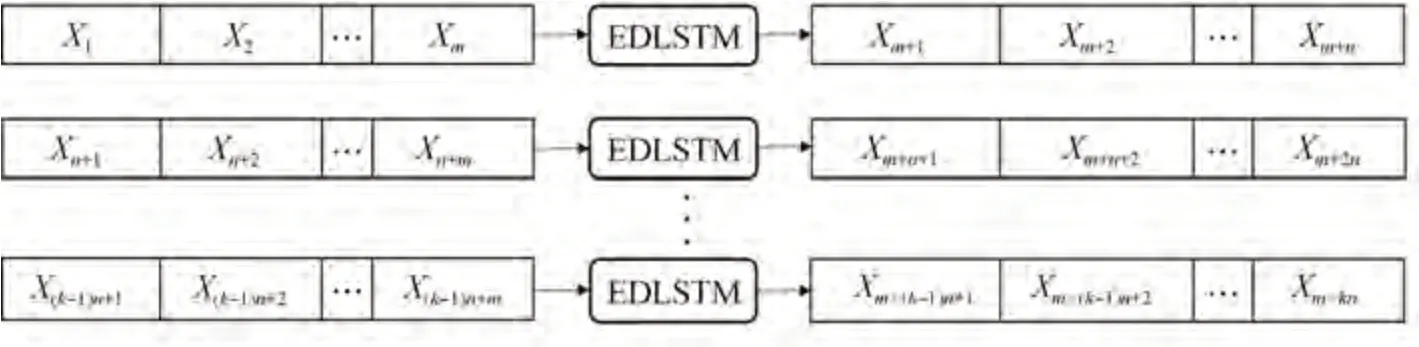
图5 EDLSTM模型迭代预测

1.4 ARIMA-EDLSTM 融合方法与计算流程

EDLSTM 模型进行预测时，随着预测序列长度增加，误差会逐渐增加，通过ARIMA 模型预测误差的线性趋势，从而修正EDLSTM 模型的预测结果，提出一种ARIMA 和EDLSTM 融合的模型。在进行锂电池RUL 预测时，先构建实车锂电池SOH 衰退的时序数据，再将时序数据按照历史时刻数据和未来时刻数据划分为训练集、误差修正集和测试集，其中训练集和误差修正集属于历史时刻数据，用于建立融合模型，测试集属于未来时刻数据，用于验证模型的预测结果。在训练集上对EDLSTM 模型进行训练。EDLSTM模型的训练过程如下：

（1）随机初始化EDLSTM 模型中的所有权重W和偏置b。

（2）设置固定步长的滑动窗口读取训练数据，将训练集中SOH 衰退数据输入，并通过编码器、解码器等前向传播得到模型的输出。

（3）计算梯度，通过反向传播更新模型中的权重W和偏置b。

（4）重复过程（2）～（3）直至达到设置的训练次数，并检查损失函数是否达到收敛。

使用训练好的EDLSTM 模型在误差修正集和测试集上分别进行预测。在误差修正集上计算EDLSTM 模型的预测误差，得到误差的一条时序数据，数据长度即误差修正集的集合长度，使用ARIMA 模型对误差数据进行拟合，并在测试集上对误差趋势进行预测，得到EDLSTM 模型在测试集上的预测误差，将 ARIMA模型预测的误差趋势修正到EDLSTM模型的预测结果中，得到最终的预测结果。

ARIMA-EDLSTM 融合模型的预测流程如图6所示。

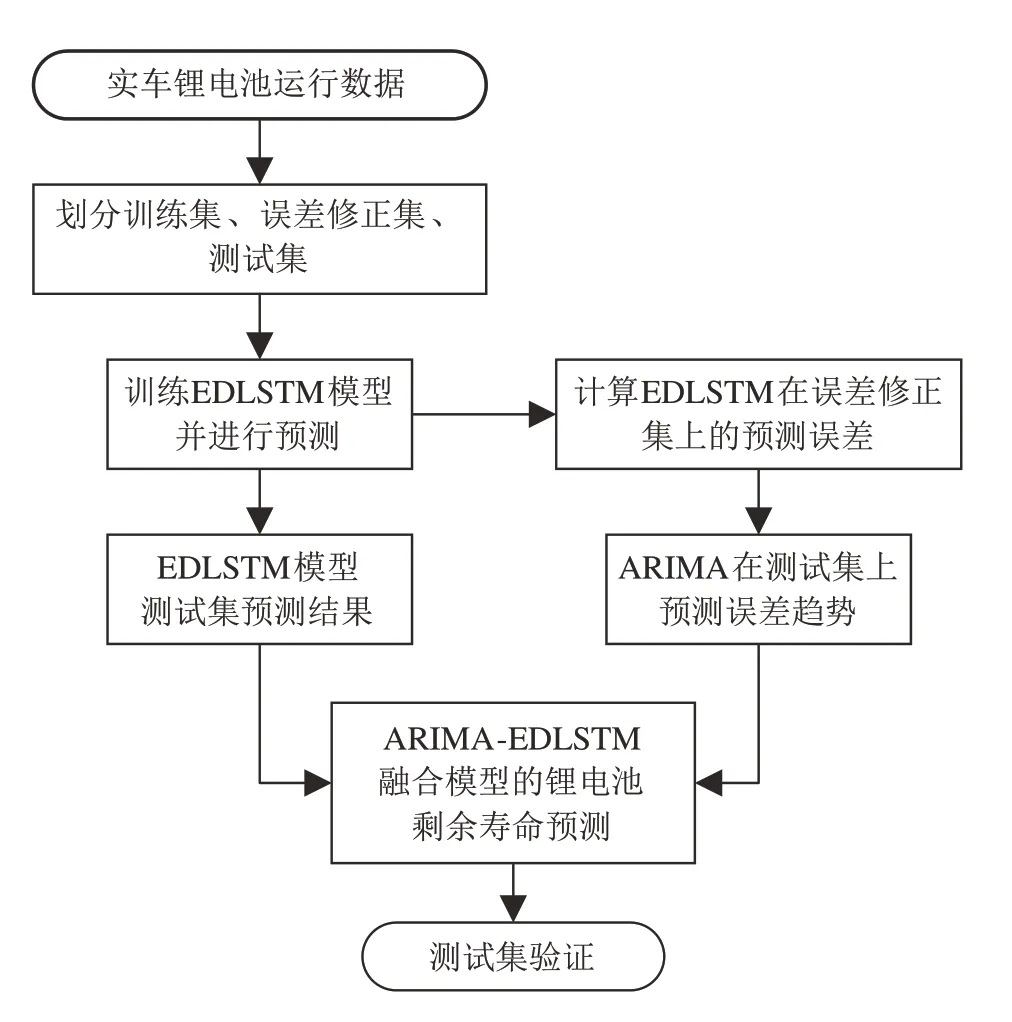
图6 ARIMA-EDLSTM 融合模型预测流程

2 基于实车数据的验证

2.1 实车数据预处理与训练集划分

锂电池数据来自同一车型的4 辆纯电动营运车辆，运行时间为9 个月，实车监控的电池数据每10 s上传记录一次，数据形式均为基于时间的序列数据，包括采集时间、行驶里程、电压、温度、SOH和剩余电量（SOC）等。

对于实车的锂电池RUL 预测，本质是预测锂电池SOH 在未来一段时间内的下降趋势，计算直接采用实车电池管理系统（BMS）采集并上传的SOH值，在BMS中SOH按照容量进行计算：

式中：Caged为当前锂电池的容量；Crated为电池额定容量，在BMS中，锂电池额定容量一般通过出厂进行设置，锂电池当前容量一般通过充电过程计算得到。

由于实车数据中BMS 采集的精度为1%，无法反映小于1%的SOH 变化量，为更好地符合锂电池SOH 实际的衰退情况，使用S-G 滤波器对SOH 衰退曲线进行平滑，平滑前后的SOH 衰退曲线如图7所示。

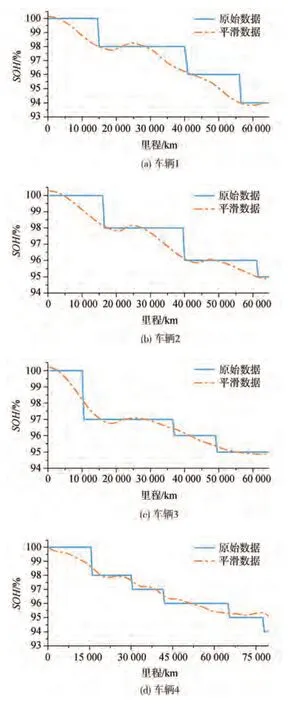
图7 SOH衰退曲线

使用实车锂电池运行数据进行ARIMAEDLSTM 模型验证时，每台车按照500 km 等间隔划分样本点，车辆1、车辆2 和车辆3 共有130 个样本点，其中前60 个划分为训练集，中间35 个划分为误差修正集，后35 个作为测试集。车辆4 共有160 个样本点，其中前70 个划分为训练集，中间40 个划分为误差修正集，后50 个作为测试集。用于对比的其他模型，将训练集和误差修正集合并作为训练集，测试集的划分不变，总的预测比例超过了历史时序数据的35%。

2.2 模型参数设置与评价指标选取

EDLSTM 模型基于Tensorflow 和Keras 深度学习框架建立。作为编码器和解码器的LSTM 隐藏层数均为1，隐藏层神经元个数均为64。使用Relu 函数作为激活函数，MSE 作为损失函数，Adam 作为优化器，batchsize 设置为10，设置训练次数为200次，用于对比的单步迭代预测的LSTM 模型内部参数设置与上述一致。EDLSTM 模型的编码器输入序列长度设置为10，解码器输出序列长度设置为5，在进行预测时，设置一个固定长度为10 的滑动窗口，不断按输出序列的长度5 进行滑动，将预测值作为下一次预测的部分输入值，迭代预测直至预测终点。统计模型 ARIMA 基于Pmdarima 库建立，采用AIC 指标筛选最佳模型。

为客观评价ARIMA_EDLSTM 的预测性能，采用两种具有代表性的误差评价标准，分别是均方根误差（RMSE）和平均绝对百分比误差（MAPE）。计算公式为

式中：Fi为第i个预测值；Ri为第i个真实值；n为时序数据的样本点个数。RMSE和MAPE的值越小代表预测误差越小，精度越高，模型的预测性能越好。

2.3 锂离子动力电池剩余使用寿命预测分析

为验证ARIMA_EDLSTM 融合模型的预测性能，选取ARIMA、EDLSTM 和单步预测的LSTM 进行对比，各模型的锂电池剩余寿命预测误差见表1。4 台车辆锂电池剩余使用寿命最终预测的结果如图8所示。

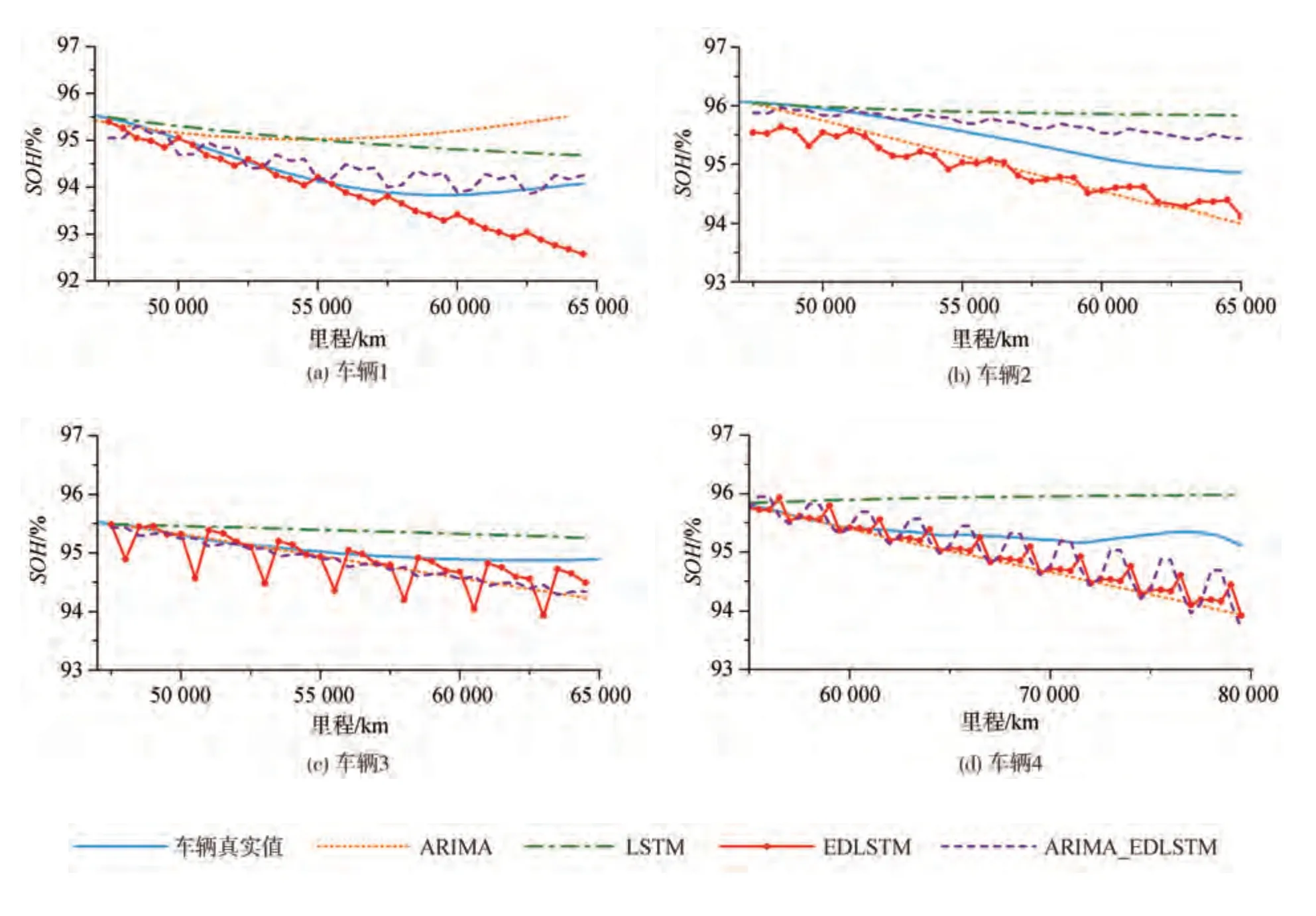
图8 各模型预测结果

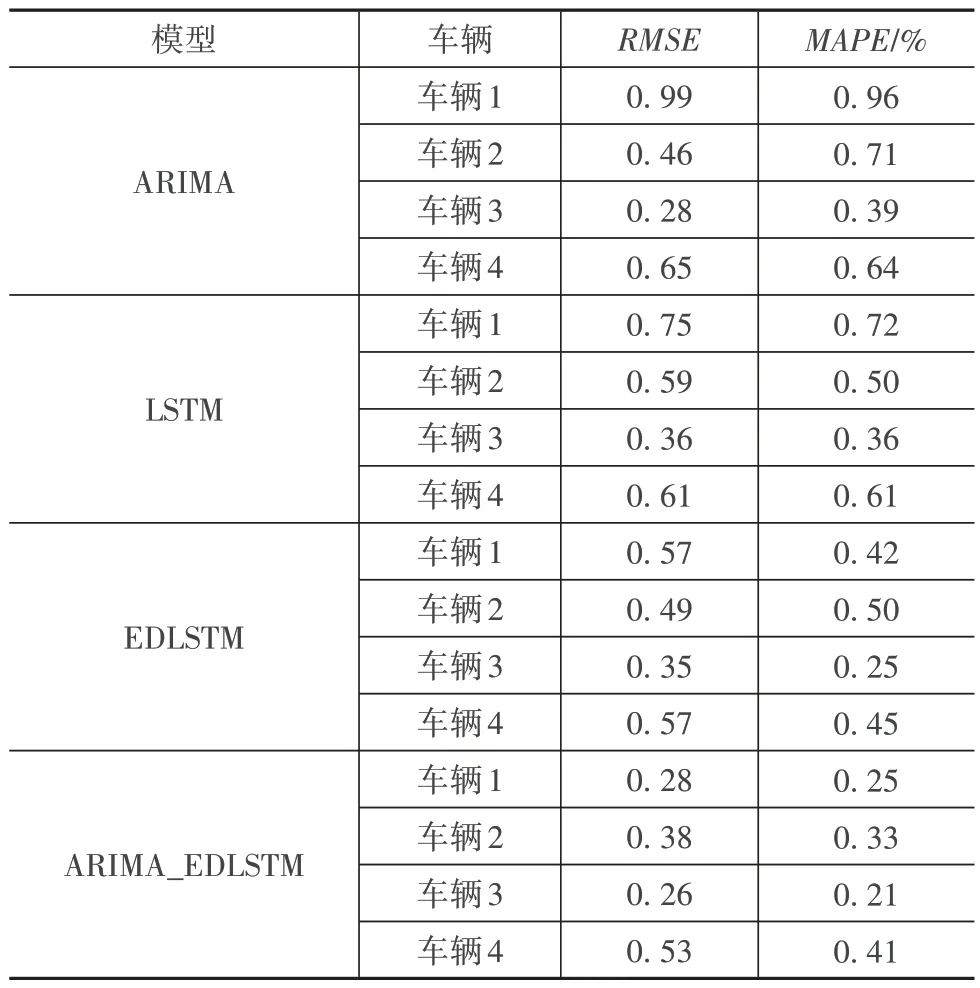
表1 各模型预测误差

EDLSTM 模型在4 台车辆上的平均RMSE和平均MAPE值均小于LSTM 模型。LSTM 模型在4 台车上的RMSE平均为0.58，EDLSTM 模型在4 台车上的RMSE平均为0.50，下降了约14%；LSTM 模型在4 台车上的MAPE平均为0.55，EDLSTM 模型在4 台车上的MAPE平均为0.41，下降了约25%，表明EDLSTM 模型能有效减少单步迭代预测产生的累积误差。

ARIMA_EDLSTM 融合模型的预测精度明显提高，在4台车上预测的RMSE和MAPE值平均为0.36和0.3，相较于LSTM 模型分别下降了38%和45%，相较于EDLSTM 模型分别下降了28%和27%。各类方法的预测结果误差如图9 所示。4 辆电动汽车的锂电池运行数据存在明显不同的衰退趋势，但模型在4 辆车上均取得了相较于对比模型更高的预测精度，可以说明ARIMA_EDLSTM 融合模型方法具有一定的普适性。

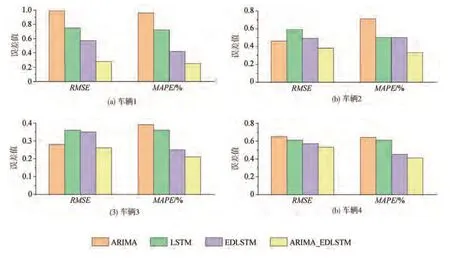
图9 模型预测效果对比

3 结论

针对实车数据驱动的锂离子动力电池剩余使用寿命预测问题，基于现有深度学习和误差分析理论，提出了ARIMA-EDLSTM 联合预测解决方案，建立了从序列到序列的锂电池剩余使用寿命预测通用方法和流程，完成了实车数据预处理、模型搭建、模型训练、模型预测和预测结果分析。该方法通过减少预测次数，控制多次预测产生的累积误差，并通过预测误差趋势对最终预测结果进行修正，实现了较长期的预测过程，并有效保证了预测精度。

通过对比ARIMA、LSTM、EDLSTM 以及本文ARIMA-EDLSTM 方法在实车数据驱动下的预测误差RMSE和MAPE，表明该方法能够适应实车运行的工况，且预测精度有大幅提升。实例数据预测结果表明，与对比方法相比，本文预测方法平均RMSE降低了28%～39%，平均MAPE降低了27%～56%。