基于模型的重型商用车空气悬架故障检测与隔离*

李 凯 陈 磊

(1.包头职业技术学院 电气工程系,内蒙古 包头 014030; 2.北奔重型汽车集团有限公司,内蒙古 包头 014030)

重型商用车后桥空气悬架系统使用气囊代替钢板弹簧,工作时,依靠安装在车架和车桥之间的高度传感器检测车辆高度的变化,进而控制充放气一体旋转滑阀动作,以此调节气囊的充放气状态,进而实现车辆承载和高度的调节。空气悬架的应用使得重汽汽车具有更好的行驶平顺性和道路友好性,而且可以调节车身高度,提高车辆和零部件的使用寿命。[1]而且根据国家强制标准GB7258-2017《机动车运行安全技术条件》规定,自2020年5月1日开始生产的车辆,总质量12吨以上的危险货物运输货车的后轴应装备空气悬架。无论是基于法规的要求还是实际性能的提高,重型汽车匹配空气悬架的占比必将提高。

从结构上看,空气悬架是以气囊(主要成分:橡胶)为核心的气动系统,是重型汽车承载和衰减振动的关键部件。由于磨损、老化、泄露等原因导致空气悬架系统故障,必将导致严重后果。因此,为实现车辆的舒适和安全驾驶,对空气悬架进行状态监测、故障检测与诊断非常有必要。

应用系统的故障诊断主要分为基于模型、基于知识和基于信号三类。随着故障诊断技术的发展,针对汽车空气悬架,主要应用如下:文献[2]根据空气悬架系统4个高度传感器的几何关系实现故障检测,利用基于卡尔曼滤波器的车辆横滚角和俯仰角的估计实现故障分离。文献[3]分别采用扩展卡尔曼滤波器、强跟踪滤波器和容积卡尔曼滤波器的方法设计空气悬架系统传感器典型故障的状态观测器,成功实现故障的检测和分离。文献[4]利用传感器的模型计算残差,通过对残差敏感性分析实现对传感器的故障检测与隔离。文献[5]和[6]通过建立三自由度的1/4悬架系统模型,分别采用状态观测及强跟踪卡尔曼滤波器算法(STF)实现空气悬架传感器故障检测与隔离诊断,文献[7]采用扩展卡尔曼滤波器组设计故障诊断方案,来辨识电控空气悬架系统传感器的典型故障。文献[8]综合利用车身俯仰角与侧倾角两种信息,采用状态估计的方法对ECAS的高度传感器进行了故障检测与隔离。

以上研究基本都是针对空气悬架的关键零部件高度传感器和执行器的故障诊断,且未对系统多故障情况下的可检测性和可隔离性深入探讨,因此当出现实际的故障,并不能直接明确是哪部分导致的故障。为实现空气悬架系统故障的精确检测和隔离,本文利用空气悬架系统数学模型,引入基于模型的结构分析法,借助其不依赖于系统具体参数值,仅需提供系统故障结构模型的特点,通过设定空气悬架系统关键故障,建立系统故障模型,利用DM矩阵分解分析判断系统故障的可检测性和可隔离性,进而确定最小的故障诊断传感器配置,实现系统故障的辨析与定位,设计故障诊断识别可测量传感器的集合。

1 空气悬架数学模型

电控空气悬架系统主要由电磁阀、气囊、高度传感器、MCU等[9-10]组成,其结构如图1所示。空气悬架系统的工作原理是:高度传感器检测车辆高度(车架和车桥间的距离)的变化,ECU可以综合车辆高度变化,车速、制动状态、供气压力等信息,综合信息后依据设定的逻辑,控制电磁阀动作,调节气囊的充放气,进而实现车辆承载和高度的调节。

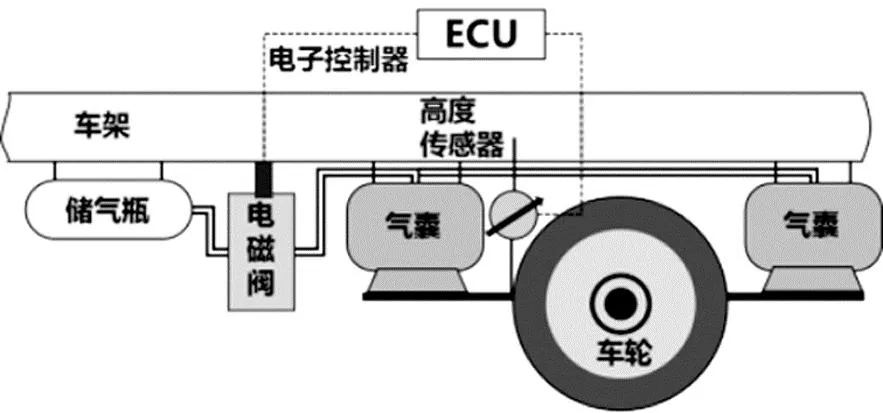
图1 空气悬架结构示意图

1.1 空气悬架系统动力学模型

空气悬架受多因素影响,具有非线性的特点,建模时简化及假设如下所述,汽车行驶过程中,轮胎对衰减振动是有影响的,但轮胎的阻尼与悬架系统减振器阻尼相比,对系统影响占比小,故建模时忽略轮胎阻尼的影响,只考虑其刚度的影响,且认为轮胎的刚度是线性的。建模过程中忽略发动机,传动轴及转向系统对悬架系统振动的影响。由于重型汽车单轴一侧两个气囊共用一个高等传感器,因此两个气囊的充放气状态一致,故可以等效为一个气囊处理。

基于上述分析,重型汽车中/后桥1/2动力学模型简化如图2所示。

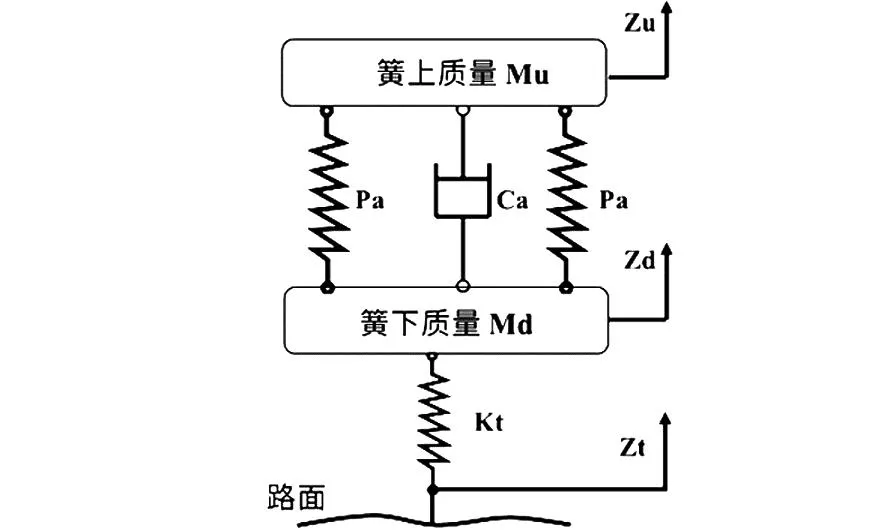
图2 1/2车桥动力学模型示意图

根据牛顿第二定律可得空气悬架系统的动力学模型,关系如下式(1)所示。

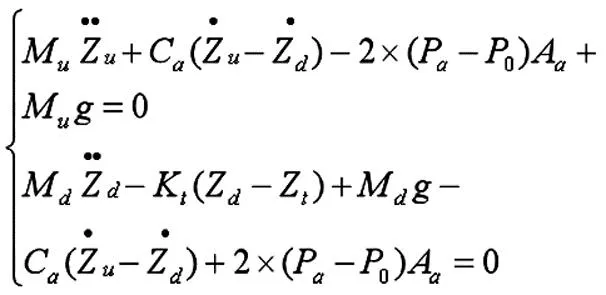
(1)

式中,Mu和Md分别表示等效簧上质量和簧下质量,Zu和Zd表示两个等效质量块离开平衡位置的位移,Zd表示道路地面激励位移,Ca表示悬架系统等效阻尼系数,Aa表示气囊的等效横截面积,Pa表示气囊中气体的绝对压力,P0表示气囊外部环境气压。

上式(1)中输入是地面道路的激励,输出是簧上质量的运动参数(包括位移,速度和加速度),想要求解式(1),需确定其中的系数,除了气囊中气体的绝对压力Pa,其余参数都可近似处理为常系数。为了确定P1,需要建立气囊模型,可通过分析其对应不同工况的热力学状态来确定。

1.2 气囊模型

考虑到车辆的运行状态和气囊的材料特性,悬架工作过程较快,因此可认为气囊为绝热状态。空气悬架工作过程中,气囊的工作状态由电磁阀控制,分别有充气状态,排气状态和电磁阀关闭3种状态。电磁阀充气和排气状态时,气囊为变质量开口系统;电磁阀关闭时,气囊为定常质量系统绝热状态(电磁阀既不充气也不排气)。充放气时,根据热力学第一定律,忽略气体流速和高度变化的影响,[11]气囊的开口变质量系统模型如下式(2)所示,

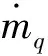
电磁阀关闭时,气囊为定常质量绝热系统,公式(2)左侧质量变化为0,V0表示气囊内气体相对压力为0时气囊的容积,此时方程为理想气体绝热方程,可简化如下式(3)所示。

气囊内压力可表示为如下式(4),

气囊的容积可表示为如下式(5),

Vq=V0+Vz(Zu-Zd)

(5)

式中,Vz表示气囊容积随高度的变化率。

气囊的横截面积可表示为如下式(6),

Aq=A0+Az(Zu-Zd)

(6)

式中,A0表示气囊内气体相对压力为0时气囊的等效横截面积,Az表示气囊容积随高度的变化率。

综上所述,当电磁阀关闭时,联立公式(1)、(4)、(5)和(6),可以获得簧上质量的运动参数与气囊压力、气囊高度及其变化率的关系。

而当电磁阀充气时,由公式(2)可知,气囊压力还与充放气口的质量流量有关,因此需要确定质量流量,故还需要建立气体经过储气瓶、电磁阀以及管路的数学模型。

1.3 充放气管路模型

气体质量流量经过储气瓶、电磁阀以及管路到达气囊的过程描述非常复杂,本文依据文献[12]并按照节流孔等效可得公式(7)。

式中,Pc表示储气瓶的气体压力,Cm表示等效节流系数。

通过上述,可以建立储气瓶压力和气囊压力之间的关系。

2 空气悬架故障模型

故障发生时,过程中至少一个特征量出现了不允许的偏离,超出了可接受的范围。故障是一种可能导致系统失灵或失效的状态。考虑到故障对过程模型的影响,可将故障分成加性故障和乘性故障。加性故障表现为故障信号与过程变量的和(如传感器的偏置导致的固定偏差信号),乘性故障表现为故障信号与过程变量的乘积(如前文中公式(1)中过程变量参数的改变)。

根据已有文献及企业数据,对空气悬架各个组件的故障进行分析,确定空气悬架关键故障为电磁阀故障、高度传感器故障,设定的故障类型如下表1所示。

表1 故障描述

根据上述空气悬架数学模型和故障变量的定义,将故障变量融入系统数学模型,令路面的输入u=Zt为已知量,建立故障模型如式(8)所述。

式(8)中,yZS表示高度传感器的测量值。x1=Zu,x2=Zd,x3=Zd,x4=Zu-x3,x5=Pa,x6=Va,x7=Aa,x8=m,x9=Pc,x10=Tg。以上10个状态变量构成故障模型的未知变量集合,未知变量的系数都是可求的,且假定为固定常数。e1～e9构成故障模型的方程组集合M。集合M和X的关系矩阵如下图3所示,关系矩阵中0表示方程中不包含未知变量,若包含变量,则分别取方程e的下角标和未知变量的下角标作为关系矩阵元素的值,如11表示方e1程中含有未知变量x1。

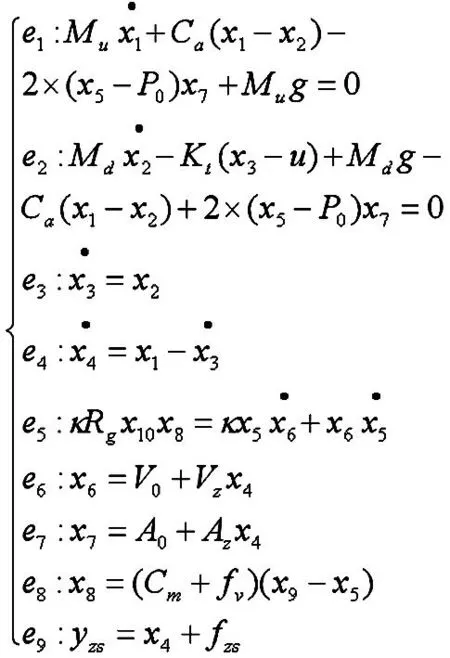
(8)

图3 关系矩阵示意图

3 故障的检测性与隔离性分析

基于结构分析的故障诊断方法[13-15],就是利用上述关系矩阵进行DM分解(通过交换原矩阵的行和列来获得分块的上三角矩阵),以判断故障的可检测性和可隔离性。

MATLAB中DM分解的步骤如下,首先将表2中关系矩阵输入MATLAB,即令A=[11 12 0 0 15 0 17 0 0 0;21 22 23 0 25 0 27 0 0 0;0 32 33 0 0 0 0 0 0 0;41 0 43 44 0 0 0 0 0 0;0 0 0 0 55 56 0 58 0 510;0 0 0 64 0 66 0 0 0 0;0 0 0 74 0 0 77 0 0 0;0 0 0 0 85 0 0 88 89 0;0 0 0 94 0 0 0 0 0 0];然后令[p,q,r,s,cc,rr] = dmperm(A);之后令DMA=A(p,q);最后根据r(行)和s(列)的值可得到分块的上三角矩阵。

3.1 检测性分析

根据文献[14]所述,当故障所在的方程属于上述关系矩阵中的超定部分,则该故障是可检测的。求解关系矩阵的超定部分可利用DM分解实现。

DM分解上述关系矩阵,结果如图4。求解各个块之间大小顺序关系(判断各个块大小顺序,可参见文献[15]),结果如图5所示,可知块b1具有最高的顺序,因此只要测量b1块中的变量{x9,x8,x10},即可保证所有故障均可检测。

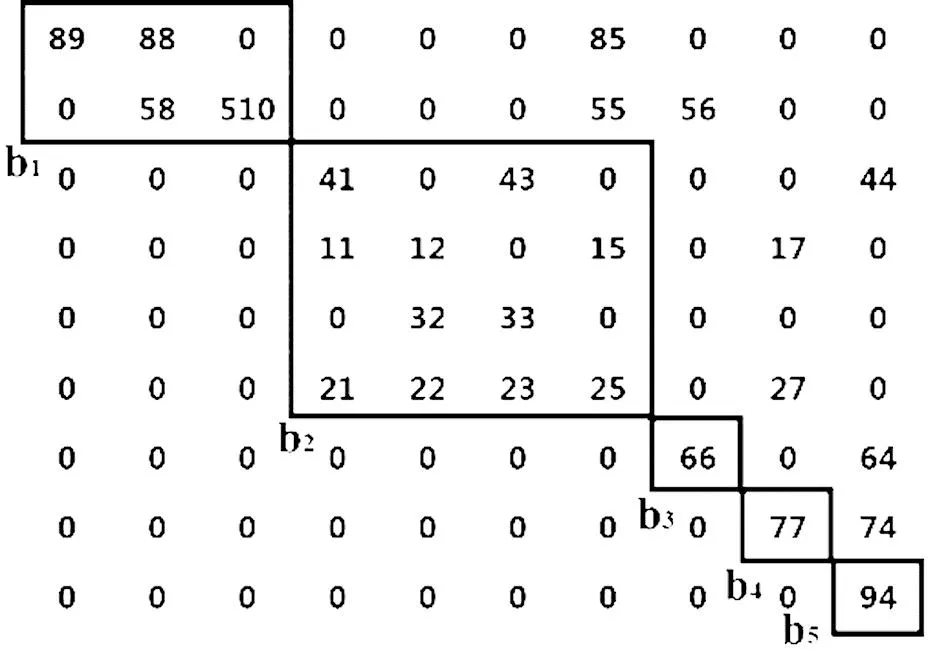
图4 DM分解后的分块矩阵

图5 分块顺序关系

根据上述可检测性的要求,需要增加的传感器,有储气瓶压力传感器和气体流量传感器和气囊进排气口的温度传感器,同时考虑增加传感器的故障fqcs、fms和fTs,yqcs表示储气瓶压力测量值,yTs表示气体流量传感器的测量值,表示温度传感器的测量值,增加的故障方程如下式(9)所示。

图6 DM分解的分块矩阵

在图3中增加式(9)中的关系矩阵后,继续利用MATLAB中dmperm( )函数进行DM分解,获得的分解矩阵如上图6所示,其为一个超定集合F={fv,fzs,fqcs,fms,fTs},因此故障集合中的每个故障属于方程组e1～e12构成的超正定集合,所以故障集合中的每个故障均是可检测的。

3.2 隔离性分析

在确定安装传感器可检测所有故障后,还需要确定所安装的传感器能否保证各个故障之间相互隔离。本例中,增加上式(9)后,由方程e1～e12组成的系统结构模型记为M,根据文献[14]所述,故障fi和fk相互隔离的条件是fi∈{M(ek)}的超定部分(可由DM分解求解),{M(ek)}表示M中去掉故障fk所在的方程ek。依据此原理,依次对故障集F={fv,fzs,fqcs,fms,fTs}执行该操作,并结合上述故障检测性的内容,当不能隔离时,继续增加传感器,继而获得能够故障相互隔离的传感器集合如下表2所示。

表2 隔离故障需要增加的传感器

根据上表2所示,可以看出故障集F中的故障{fzs,fms,fTs}可以完全隔离,但故障{fv,fpcs}彼此间不能隔离,且均需要添加相同的检测量x9,实事上x9变量,已经添加其为传感器,这里产生矛盾。

3.3 矛盾讨论

详细分析上述矛盾,发现表2中,隔离故障fv, 需要去除方程e8,此时对剩余结构DM分解,方程e11中的x9属于欠定部分,而隔离故障fpcs,需要去除方程e11,此时对剩余结构DM分解,方程e8中的x9属于欠定部分。这说明方程e8和e11不完全独立。此时回看建模时的方程e8,可以看出,建模时是将储气瓶、气路和电磁阀使用一个数学方程描述其动态行为,它们相互之间无法完全区分,这就导致相应零部件产生的故障也无法隔离。因此想要完全隔离故障{fv,fpcs},需要分别采用数学模型描述储气瓶和电磁阀的动态行为。

基于上述讨论,本文将采用式(7)描述电磁阀,增加式(10)来描述储气瓶的动态过程(根据热力学第一定律描述定容积绝热排气过程)。

式中T0表示储气瓶中的温度,并令x11=T0,Va0表示储气瓶的容积。

此时,将式(8)、式(9)和式(10)结合起来作为新的模型结构,再次进行DM分解如下图7所示。

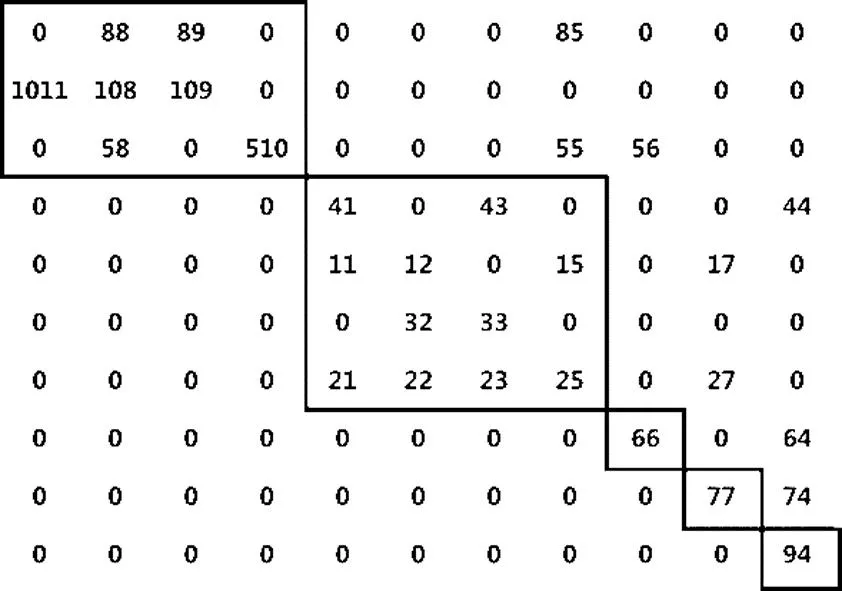
图7 DM分解的分块矩阵

根据前文所述,为保证所有故障可检测,需要可测量最高顺序块中的变量,即{x9,x8,x10,x11},融合这四个传感器的故障模型后,再进行隔离性检查,发现此时所有故障均可隔离,如表3所示。

表3 隔离故障需要增加的传感器

这样,增加可测变量{x9,x8,x10,,x11}后,所有故障均可检测和隔离。故{x9,x8,x10,x11}也是空气悬架系统所有故障可检测和可隔离的最小传感器集合。

4 结语

本文通过建立数学模型来描述重型商用车空气悬架的动态过程,然后基于结构分析法建立空气悬架系统的故障模型,对故障模型的关系矩阵进行DM分解,获得关系矩阵的分块顺序和是否超定的部分,以此判断故障是否可以检测和隔离,并且根据分块顺序可以确定为了保证检测性和隔离性需要增加的最小传感器的数量。基于结构分析法的优点如下:

(1)DM分解的运用,可以不用具体求解复杂的故障模型方程,就可以判断故障的检测性和隔离性,极大提高效率。

(2)结构分析法的运用,在故障诊断时可以更加精确的确定需要配置的传感器类型。

(3)故障模型建立后,可以根据隔离性的检测逆推系统过程模型是否完备。

以上优点将对后续搭建实际故障模型进行故障诊断提供理论支撑。