基于Jacobian+RBF的3-PTT并联机构末端精确控制方法
陈明方 黄良恩 魏松坡 郑仕高 陈中平
(1.昆明理工大学机电工程学院,昆明 650500;2.河南平原光电有限公司工程信息部,焦作 454150)
0 引言
并联机构的末端运动精度影响其应用范围[1],为提高运动精度,国内外学者提出了多种策略[2-5]。张俊等[6]提出了以几何误差源最优区间制定并联机构关键零部件精度等级及配合公差的精度设计方法。于今等[7]通过参数辨识的方法修正正向运动学,显著提高了机构的位置精度。李国江等[8]通过多种群协同进化算法补偿了并联机构的位置误差。董慧芬等[9]基于RBF设计控制器,控制了并联机构末端位置。刘毅等[10]提出了一种轮式并联调姿机器人的冗余控制策略,保障了调姿精度。覃志奎[11]提出了一种由机构末端修正位姿修正各关节变量的机构误差补偿的方法。余跃庆等[12]通过改进标准的PSO算法,补偿了机构的末端位姿。谢平等[13]利用粒子群算法修正机构的期望轨迹,并基于自适应迭代学习控制算法补偿了机构动态误差。高鹏宇[14]提出基于种群粒子群算法的静态误差补偿和基于RBF网络的动态误差补偿,提高了打捞机器人的控制精度。侯雨雷等[15]基于模糊神经网络建立机构的综合误差预估模型,提高机构的运动精度。JIAN等[16]利用激光跟踪仪测量机构末端执行器,完成了5自由度串联机构的标定。赵磊等[17]通过全局数值寻优获取机器人的误差补偿数据,完成了标定和补偿。杨强等[18]考虑机构的形位误差、转动副间隙建立了机构的误差模型。MANSOUR等[19]通过测量关节变量向量和参考位置差,完成了并联机构的标定。张宪民等[20]分析关节间隙对重复定位误差分布的影响,通过标定的方法提高了机构定位精度。孟庆梅等[21]提出了一种基于模糊神经网络的误差参数识别模型和误差补偿方法。
并联机构机械误差获取较为繁琐和困难,补偿模型复杂且模型精度不高。另外随着机构使用年限增加,机构误差也会发生不同程度的扩大,补偿方法不能满足要求。为避免上述问题,本文提出一种基于Jacobian和RBF神经网络相结合的机构误差补偿策略,并通过实测数据进行验证。
1 并联机构分析
图1a为3-PTT并联机构的模型,结构简图如图1b所示,点o、o1分别为静平台、动平台中心。机构滑块通过滚珠丝杠驱动,从而形成移动幅P。3个连杆对称布置,在静平台上投影夹角为120°。连杆两端通过虎克铰T分别连接动平台与滑块,构成PTT支链,3条支链完全相同。并联机构相关参数如表1所示。
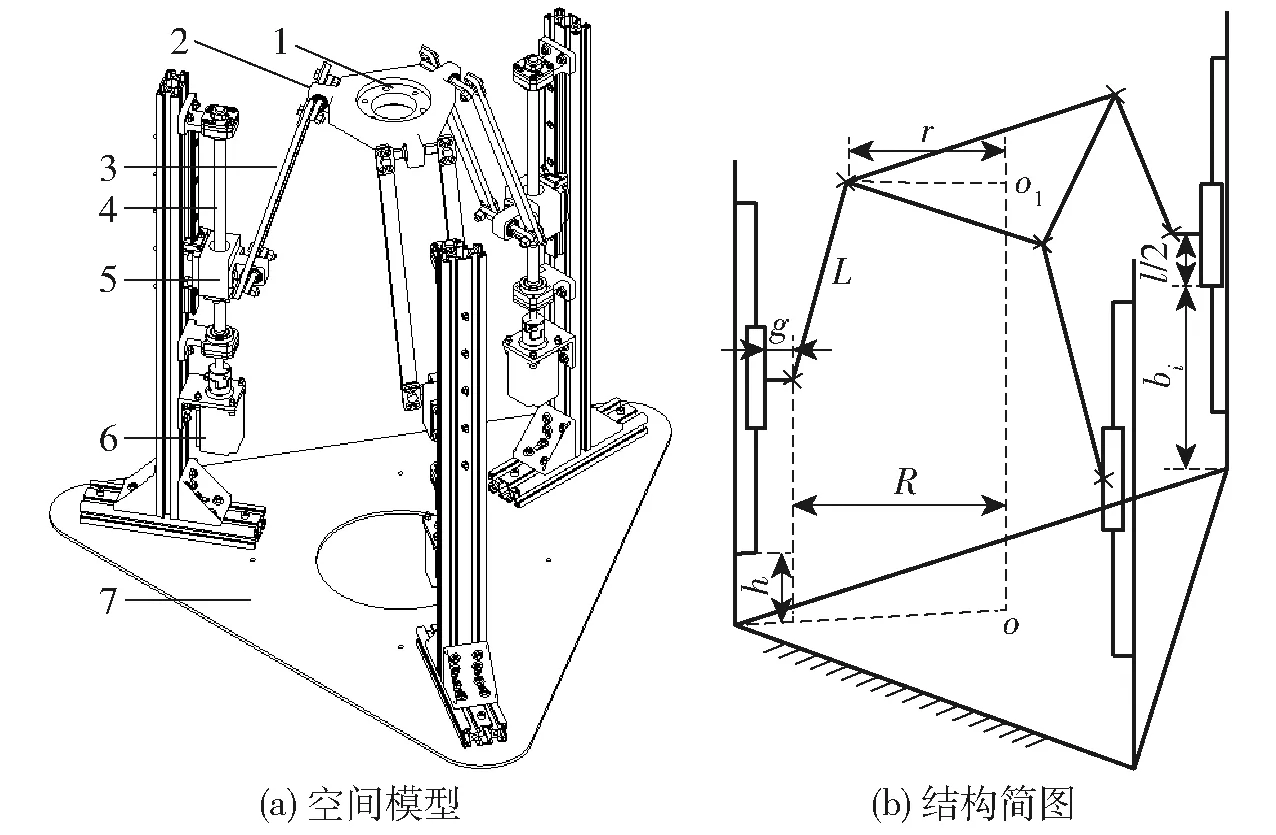
图1 3-PTT并联机构

表1 并联机构参数
1.1 逆运动学分析
图2为机构运动学模型,为求解机构逆运动学,分别以点o、o1为原点建立静、动坐标系。P1A1位于静坐标系x轴正上方且平行于x轴。
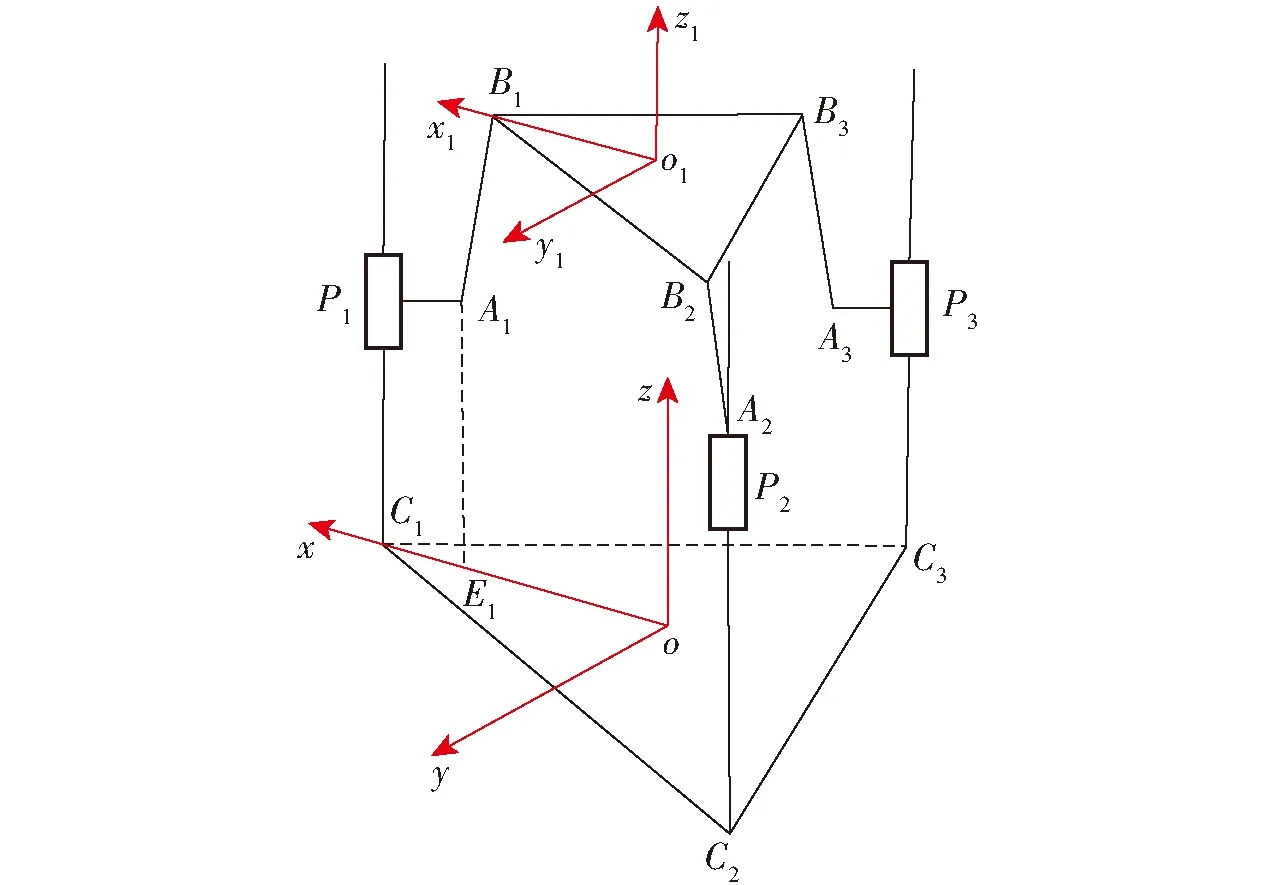
图2 并联机构运动学模型
设末端中心点o1在静坐标系中的坐标为o1=(X,Y,Z)。根据图2,表示静坐标系中Ai(i=1,2,3)的坐标,在△oo1Bi(i=1, 2, 3)中,通过封闭三角形矢量法,表示静坐标系中点Bi(i=1, 2, 3)的坐标,即可得到机构各连杆向量lAiBi(i=1,2,3)。机构动平台位置约束条件和连杆矢量满足的等量关系可表示为
(1)
如图1b所示,记滑块位置为bi(i=1,2,3)。将表1中的参数代入式(1)并化简,可得机构逆运动学方程为
(2)
式(2)简记为bi=f(R,r,L,X,Y,Z)(i=1, 2, 3)。
1.2 正运动学分析
运动学正解是根据滑块位置,求解末端点o1位置的过程,是逆运动学的反过程。根据式(2)反解出机构运动学正解,并以隐方程表示为
(3)
根据正逆解方程,设计Matlab/GUI界面。任意给定5组末端位置,分别进行正逆解计算,其算例详见表2。由表2可知,本文的正逆运动学模型正确。
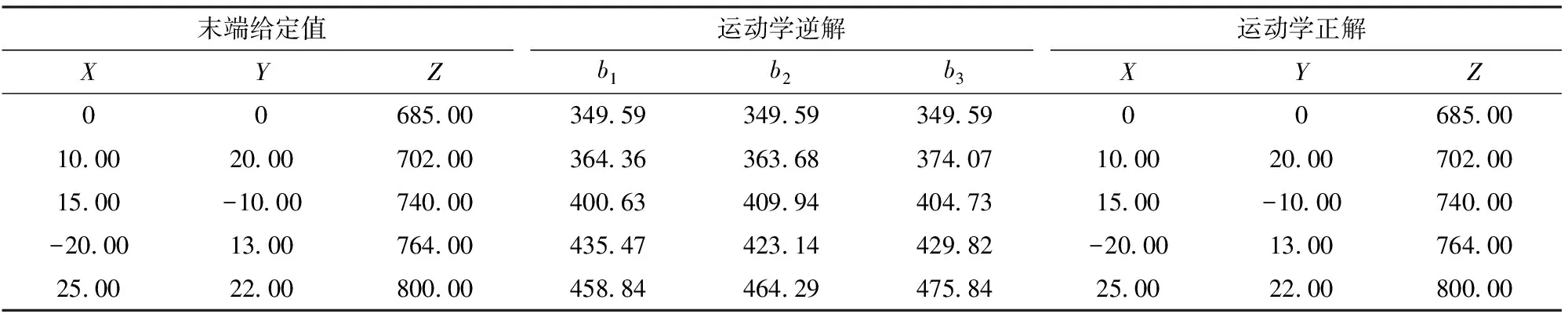
表2 运动学正逆解算例
2 末端误差补偿策略
由于机构几何误差、运动副误差、制造误差等分析及补偿方法复杂,且误差项难以完全获得,运动学标定不适用于无法修改运动学参数的场景[22]。由于机构的Jacobian能够表征机构末端与滑块位置间的误差关系,因此本文提出一种基于Jacobian和RBF神经网络的末端精确控制方法。通过对滑块位置误差的控制,补偿末端误差,以提高末端的位置精度。
2.1 Jacobian分析
Jacobian是描述机构输入、输出端的速度映射矩阵,在本机构中为表示滑块速度、末端速度间的映射矩阵。对式(2)进行时间微分,整理后得
(4)
2.2 奇异性分析
当Jacobian行列式为零时,机构将存在奇异性,因此取式(4)的行列式为
(5)
其中
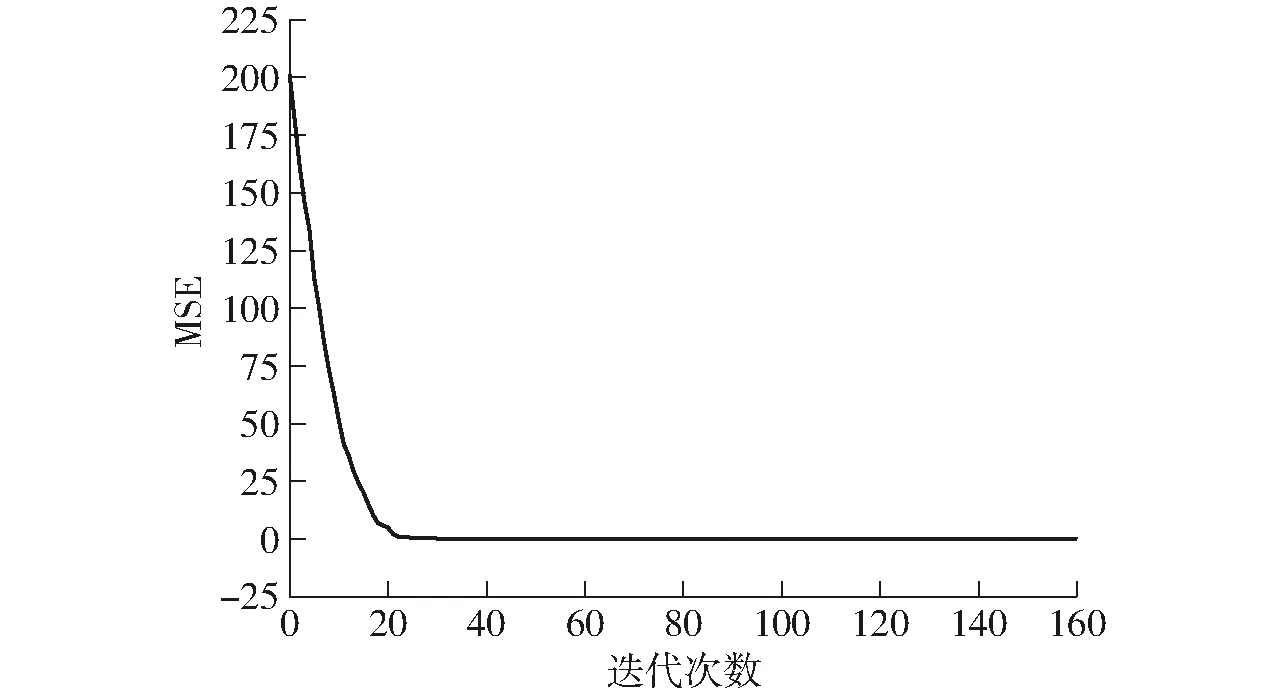
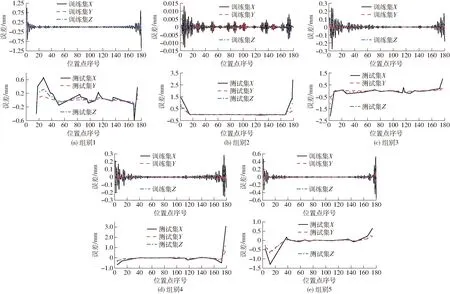
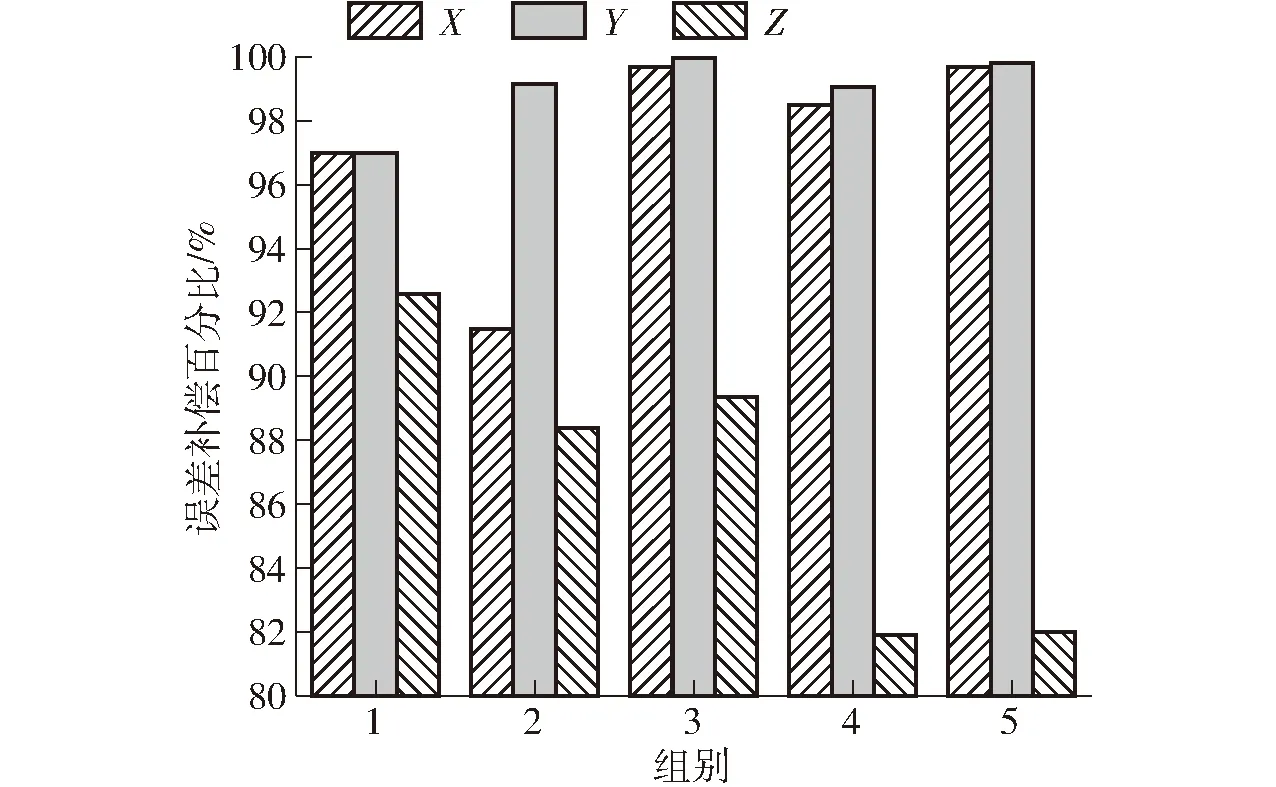
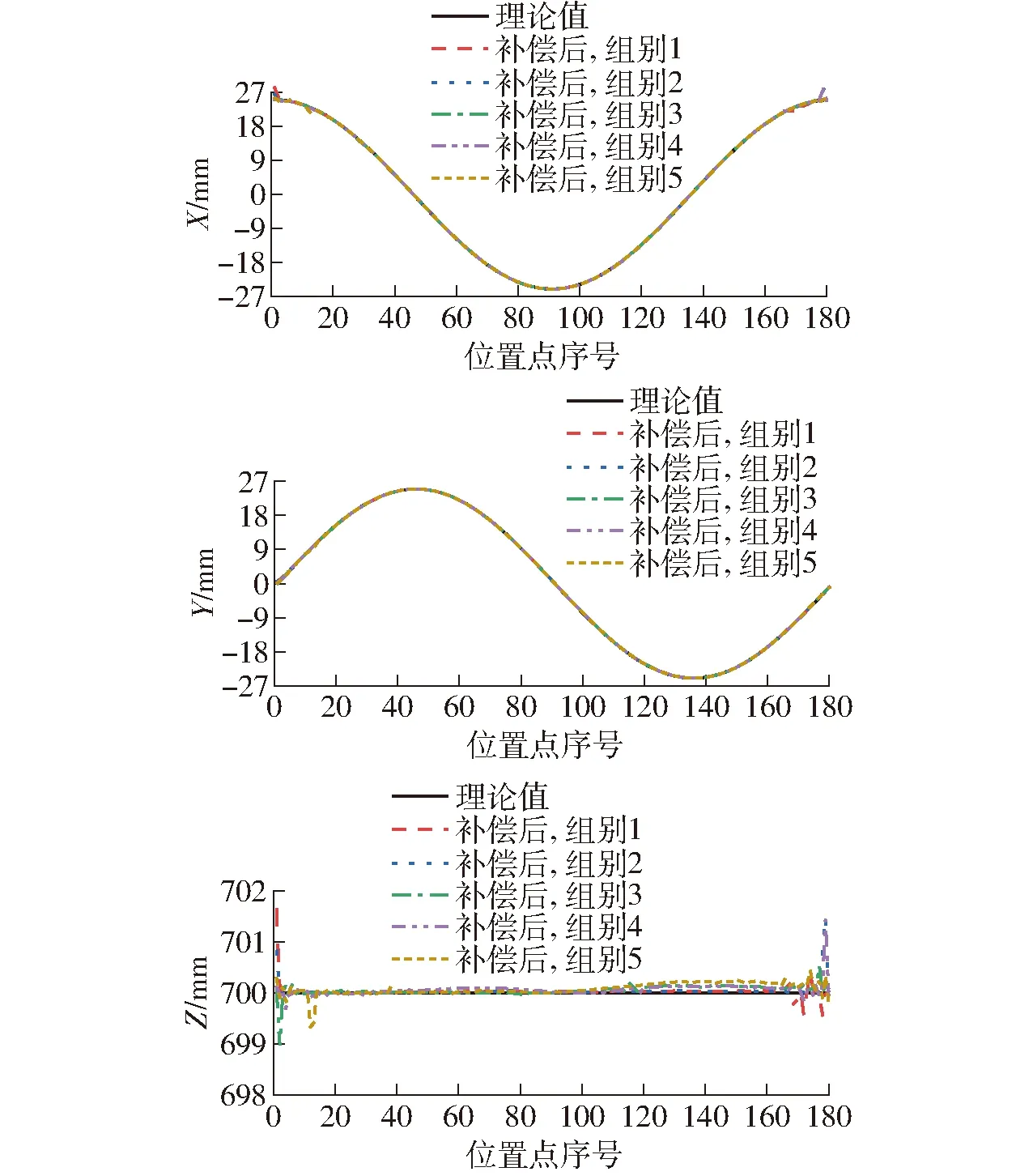
行列式为零的情况分为4种:当R=r时,机构存在约束奇异,由于r (6) 整理得 (7) 当k1、k2均为零而det(J)的其余项不为零时,可得 (8) 整理得 (9) 因此,当机构末端的运动不满足式(7)或式(9)时,机构将不存在运动奇异。 根据奇异性分析,机构的Jacobian可以表征滑块、末端的位置误差关系。设机构末端和滑块的位置误差矢量分别为Δp、Δb,则机构末端误差与滑块误差的关系为 Δb=JΔp (10) 由于机械误差的客观存在,导致机构实际运动学不等于理论运动学。因此,对于给定同一末端位置时,滑块实际位置与理论位置并不相等。 当以滑块理论位置Hm(b)驱动机构实体,其末端将完成实际运动Pm(p+Δp),其中Pm(p)为末端理论位置。为使机构末端到达理论位置Pm(p),则修正的滑块位置应为Hm(b-Δb)。由Δb与Δp满足式(10),为得出符合实际机构的运动学模型,首先,根据式(10),通过Δp与Pm(p)获得机构末端修正位置Pm(p-Δp)。进而Pm(p-Δp)通过理论逆解获得滑块修正位置Hm(b-Δb),具体为 Hm(b-Δb)=f(R,r,L,Pm(p-Δp)) (11) 其次,由于Hm(b-Δb)=Hm(b)-Δb,因此Hm(b-Δb)满足 Hm(b-Δb)=f(R,r,L,Pm(p))-JΔp (12) 根据式(12)可知,当等式右边为末端理论位置Pm(p)时,等式左边为修正滑块位置Hm(b-Δb),即式(12)为Pm(p)到Hm(b-Δb)的映射方程。因此,根据实测值将式(12)中的J变为实际值,对应的末端理论位置Pm(p)变为Pm(pa),以此得到机构实际逆解为 Hm(b-Δb)=f(R,r,L,Pm(pa))-JaΔp (13) 式中Ja——实际Jacobian矩阵 Pm(pa)——补偿后末端位置 由末端理论位置得到末端修正位置的过程和末端修正位置得到补偿后末端位置的过程互为逆过程,具体过程如图3所示。因此,由式(11)可获得Hm(b-Δb),将式(13)写入控制器,得到机构补偿后末端位置,补偿后末端位置与理论位置相等或两者的误差满足机构精度要求。 图3 末端误差补偿策略 由径向基函数(Radial basis function,RBF)设计的神经网络为径向基神经网络,也称为RBF神经网络[23]。RBF神经网络能逼近任意非线性函数,且无局部最优。本文搭建RBF神经网络,以Pm(p)和Pm(p-Δp)作为网络的输入和输出进行训练,使得网络具有由Pm(p)映射到Pm(p-Δp)的能力,给定Pm(p)后,通过RBF网络便获得Pm(p-Δp)。基于Jacobian和RBF网络的末端精确控制模型如图4所示。 图4 末端误差补偿模型 根据末端精确控制模型搭建机构末端理论位置(Pm(p)=(Xt,Yt,Zt))到机构末端修正位置(Pm(p-Δp)=(Xr,Yr,Zr))映射的RBF神经网络,网络结构如图5所示。网络输入层m=3、输出层n=3,隐含层为q1。 图5 RBF神经网络结构 隐含层选高斯函数作为激活函数,为 (14) 其中x1=(Xt,Yt,Zt) 式中x1——输入样本g1——中心向量 ε——带宽向量 因此第d1个输入层到隐含层映射为 (15) 隐含层与输出层连接权值wd1n1计算式为 (16) 式中η——学习速率,取0~1 ytn1——第n1个输出层期望值 yn1——第n1个输出层实际值 第n1个输出层实际值yn1计算式为 (17) 式中θn1——隐含层阈值 首先通过无监督学习的方式确定中心向量和带宽向量,当中心向量确定后通过有监督学习的方式进行训练确定权值向量,进一步根据式(17)即可确定网络输出。其中,径向基函数的扩展速度Sp对训练结果的影响较大,过大时虽拟合平滑,但较多神经元会被隐藏,过小会导致网络性能不佳。 为获得验证本文补偿方法的数据集,给定末端中心的运动方程为 (18) 式中r1、C——常数 α——末端运动轨迹弧度 t——末端位置点,初值为1 末端位置测量实验共计5组,实验条件如表3所示,各组实验数据采集过程如图6所示。 表3 实验条件 图6 数据采集过程 3.1.1回程误差测量及补偿 对比实验1以丝杠回程误差是否补偿为单一变量。因此,首先需测量丝杠回程误差并完成补偿,再通过激光跟踪仪测定回程误差补偿前后机构的末端位置。回程误差通过光栅尺(量程300 mm,精度1 μm)、阿尔泰USB2010型数据采集卡等完成测量,如图7所示,采集数据见表4。 图7 回程误差测量 表4 上位机数据 各支链上丝杠回程误差ej计算式为 (19) 其中 式中ej1、ej2——回程误差ejq——均值 S1——丝杠正转时数据长度 S2——滑块反向过程数据长度 S3——丝杠反转时数据长度 u——电机正转圈数,取10 由式(19)求得末端受不同负载时,各支链上丝杠回程误差ej见表5。 表5 丝杠回程误差 通过软件补偿方法在滑块反向运动时给定补偿量,完成回程误差补偿。将回程误差补偿前、后末端第k次位置,分别记为F1k和F2k(k=1,2,…,7),滑块位置分别记为E1k和E2k(k=1,2,…,7)。回程误差补偿前、后以滑块移动固定行程时的重复定位精度验证补偿效果,衡量指标为单位行程下的重复定位误差,分别记为σ1和σ2。具体求解过程如图8所示。 图8 重复定位误差求解流程图 根据重复定位误差求解单位行程下重复定位误差,计算式为 (20) K——滑块行程 求解结果见表6。由表6可知,回程误差补偿后滑块的重复定位精度更高。 表6 单位行程重复定位误差 3.1.2数据测量 数据测量方案如图9所示。R-20 Radian型激光跟踪仪具有自动跟踪锁定靶球的功能,将激光跟踪仪放置在并联机构周边的合适位置并连接上位机(PC机)软件TrackerClib,获取靶球的位置坐标。首先,驱动机构至零位,并将激光跟踪仪的靶球固连在机构末端的中心。其次,在控制系统中分别写入回程误差补偿前和补偿后的机构末端控制程序,通过伺服电机控制机构运动至预定位置。最后,利用激光跟踪仪连续记录靶球的位置坐标,在TrackerClib中获得靶球在激光跟踪仪坐标系下的位置坐标,即机构末端中心在激光跟踪仪坐标系中的坐标。根据激光跟踪仪坐标系与机构静坐标系的变换矩阵,获得机构末端中心在静坐标系中的坐标数据,坐标数据分布如图10所示。 图9 末端位置测量 图10 测量数据均值分布 对比实验2是以末端受不同负载为单一控制变量,即组别3~5。图11为组别3~5的末端位置测定实验方案,为降低偶然误差的影响,实验重复进行7次测量,并以均值代替实测值。 图11 不同负载时末端位置测定 根据激光跟踪仪坐标系与机构静坐标系间的变换矩阵,获得机构末端在静坐标系中的坐标。表7为组别3中部分末端位置点的坐标值,测量结果的均值分布情况如图12所示。根据实测坐标与理论坐标即可获得末端轴向(x轴)、径向(y轴)的位置差。为避免由于机构尺寸(l、hr、hR等)导致竖直方向(z轴)的位置差不准,机构竖直方向的位置差由各测量位置点与初始位置点获得。 表7 激光跟踪仪测量值 图12 测量数据均值分布 根据实测数据获得末端修正位置,并搭建RBF神经网络,设定网络均方误差为零。以末端理论位置、修正位置分别作为网络输入、输出进行训练,训练完成后,实验1~5网络径向基函数的扩展速度Sp为3.8、3.4、3.4、3.6、3.5。 随机选取160组数据作RBF网络的训练集,其余20组作测试集。RBF网络的MSE曲线如图13所示,由图13可知,当训练达20次后,RBF网络便有了较好的逼近效果。 图13 MSE变化曲线 各组实验中的计算修正位置与训练所得修正位置之间的偏差如图14所示。由图14可知,将RBF训练的修正位置Pm(p-Δp)替代计算修正位置,输出精度满足要求。 图14 各组实验RBF网络训练效果 由RBF神经网络训练的修正位置与理论逆运动学反解出滑块的修正曲线如图15所示。 图15 滑块修正位置曲线 将滑块的修正位置代入实际逆解式(13),得到机构补偿后的末端位置。表8为误差补偿前、后部分末端位置点的误差。补偿后末端位置误差与未补偿时的末端位置误差分布如图16所示,由图16可知,误差补偿后的末端位置精度明显提高。 图16 误差曲线 表8 补偿前后末端误差对比 以误差补偿百分比评价末端误差的补偿效果,其计算式为 (21) 其中 式中Ab、Aa——误差补偿前、后平均误差 e1t、e2t——误差补偿前、补偿后末端位置误差 Pg——末端误差补偿百分比 末端误差补偿百分比如图17所示。由图17可知,本文提出的末端误差补偿算法,具有较好的补偿效果。各组实验中末端轴向(x轴)、径向(y轴)的位置误差均降低90%以上、竖直方向(z轴)的位置误差均降低80%以上。图18为补偿后末端运动曲线,与理论曲线吻合度较高。各组实验结果均证明了本文补偿方法的有效性,本文得到的滑块修正位置可用以控制机构末端的运动,提高了末端位置精度。 图17 误差补偿百分比 图18 补偿后末端曲线 (1)完成了一种3-PTT并联机器人的运动学分析。 (2)建立了机构的Jacobian,并分析了Jacobian的约束奇异和运动奇异。分析表明机构不存在约束奇异,当机构的运动不满足式(7)或式(9)时,无运动奇异。 (3)提出了一种基于Jacobian和RBF网络的末端精确控制策略。分别通过RBF获取的末端修正位置和Jacobian获得滑块的修正位置,得到了一种可模拟机构实际运动的运动学模型。 (4)设置了两种对比实验。验证了本文控制方法的有效性。补偿结果表明,各组实验中末端轴向(x轴)和径向(y轴)的位置误差均降低90%以上,竖直方向(z轴)的位置误差均降低80%以上。2.3 基于Jacobian和RBF网络的补偿策略
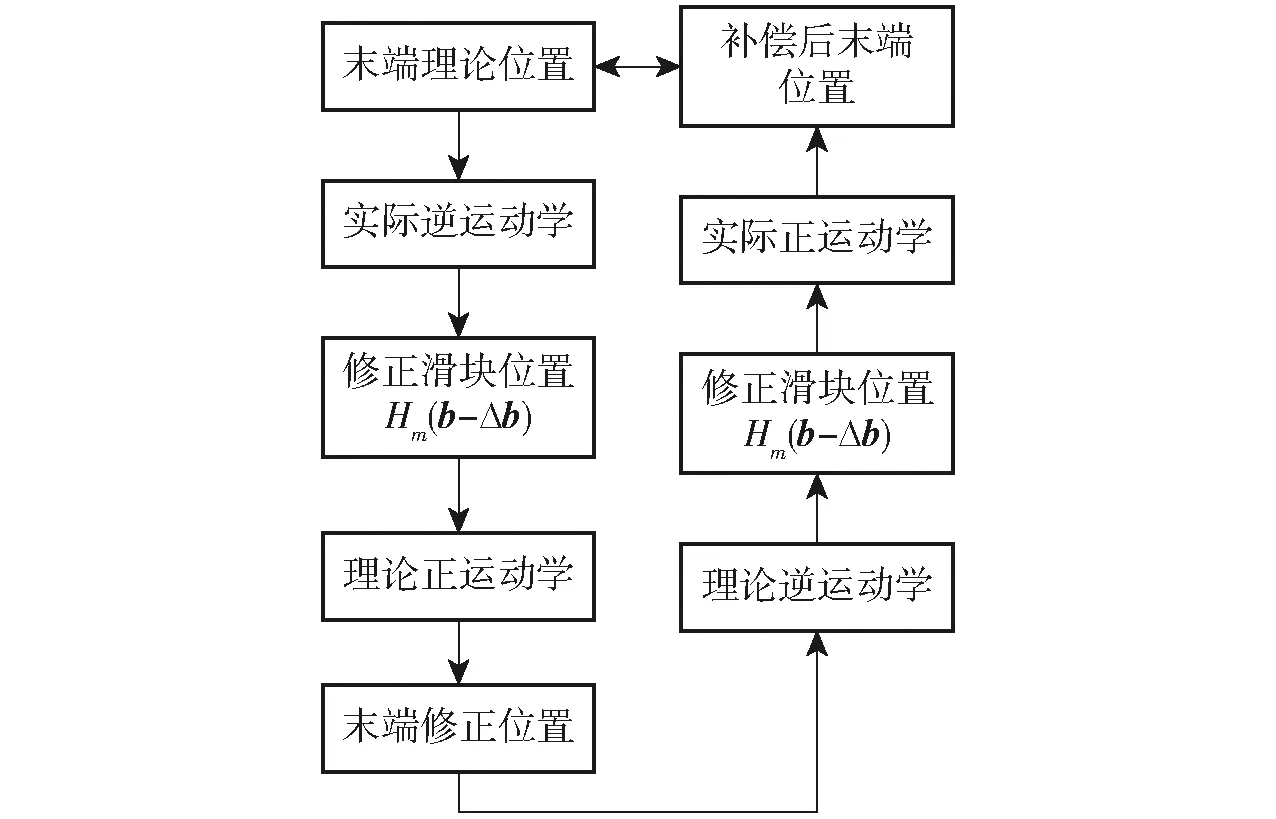

2.4 RBF神经网络建立

3 实验验证

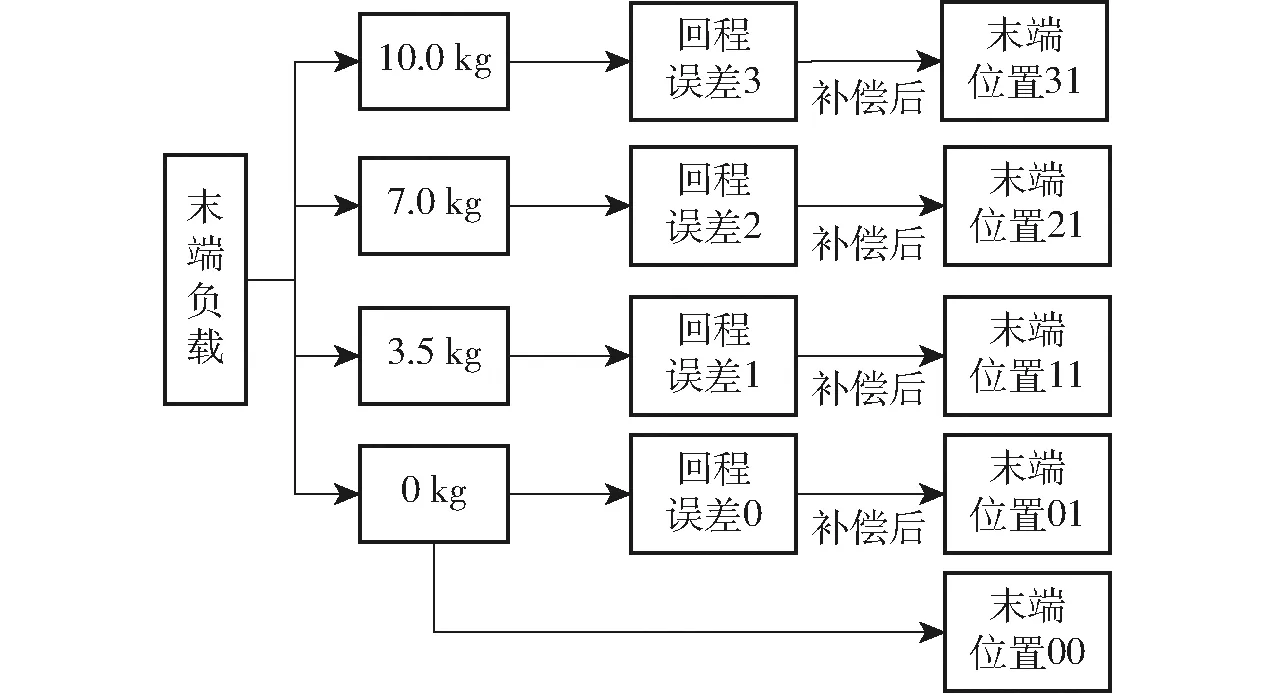
3.1 回程误差补偿前后末端位置测定

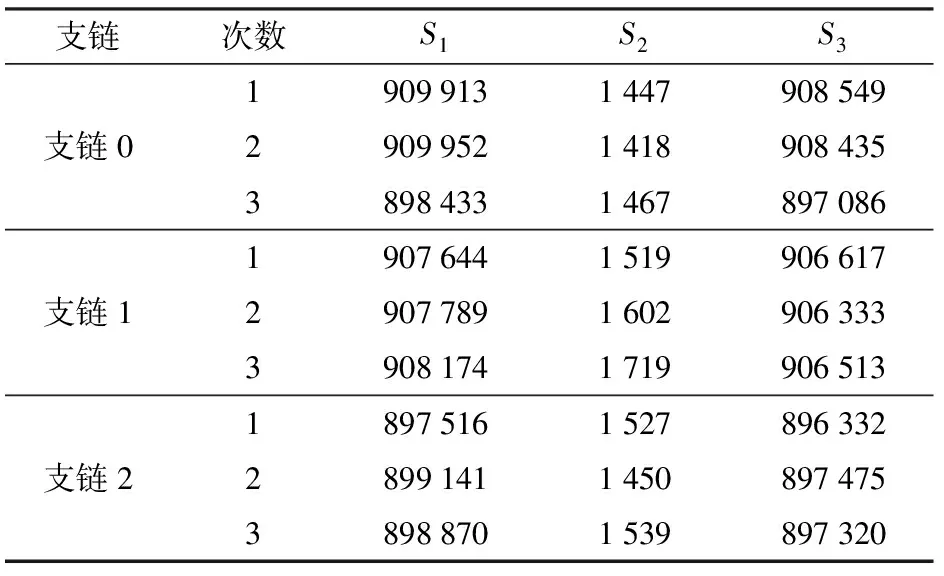
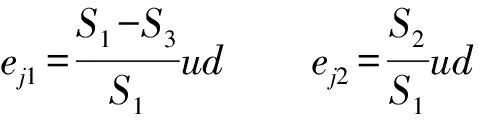
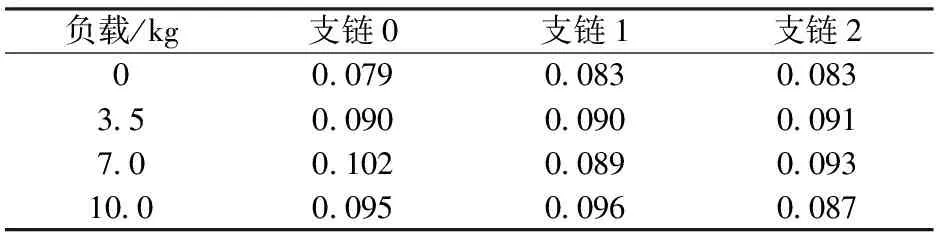
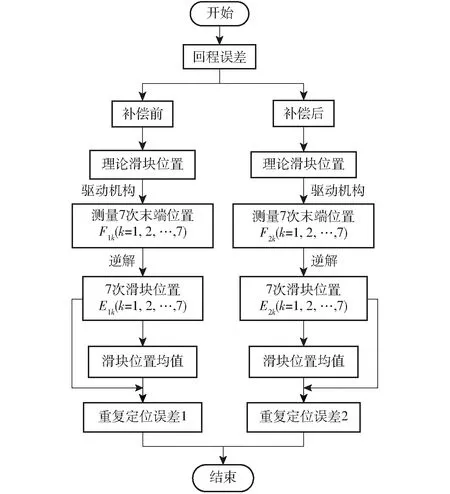

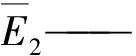


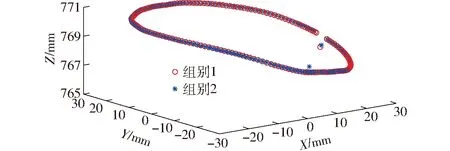
3.2 末端受不同负载时位置测定

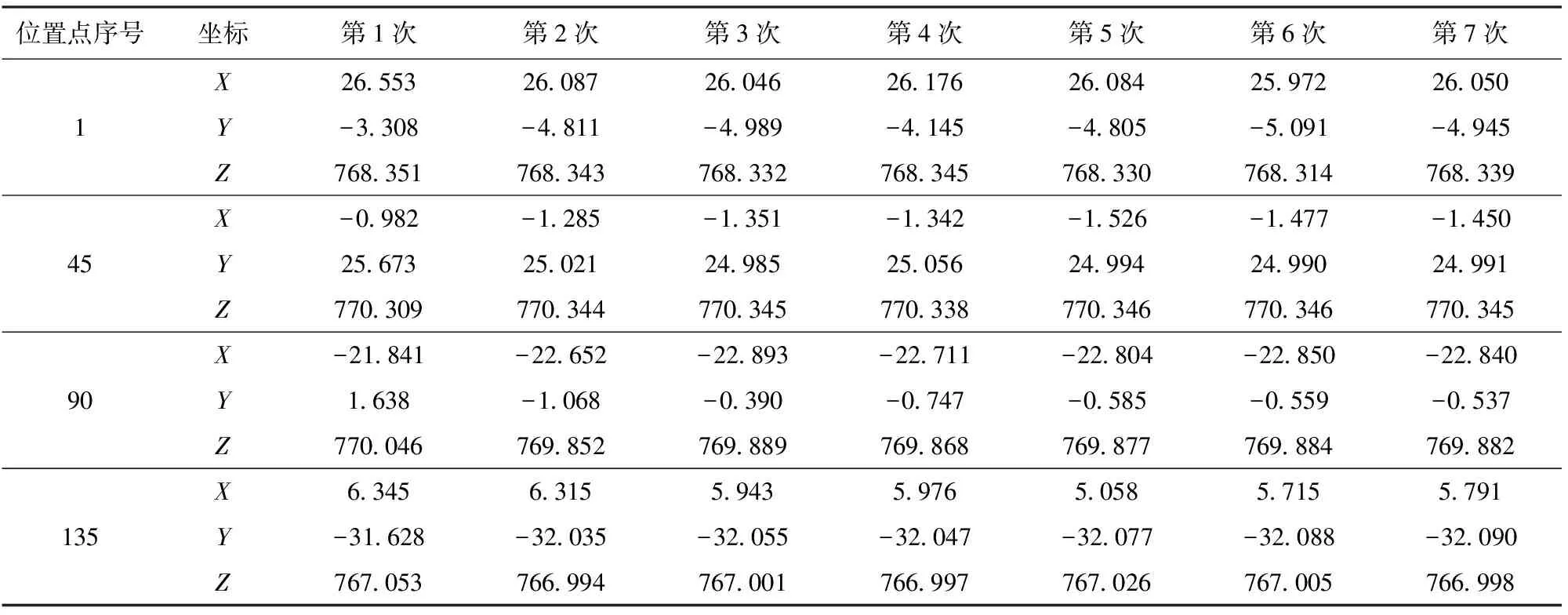

3.3 结果分析



4 结论

