基于高斯-广义双曲混合分布的非线性卡尔曼滤波

王国庆 杨春雨 马 磊 代 伟

以卡尔曼滤波 (Kalman filter,KF) 为代表的状态估计算法是信息融合、导航定位、目标跟踪、智能电网等领域的关键技术[1-3].经典的KF 针对线性高斯系统设计,能够获得多种统计意义下的最优估计值.随后KF 扩展到非线性系统的状态估计,代表性算法包括扩展卡尔曼滤波 (Extended KF,EKF)、无迹卡尔曼滤波 (Unscented KF,UKF) 和容积卡尔曼滤波 (Cubature KF,CKF).EKF 直接采用一阶泰勒展开将非线性函数线性化,当非线性程度较强时估计精度和稳定性难以保证.UKF 和CKF 均是采用确定性采样点来计算非线性积分,从形式上讲CKF 是UKF 算法的一种特例,两者较EKF 有更好的估计精度[4].以上算法均是针对高斯噪声系统设计,然而在很多具体应用中传感器噪声会偏离高斯分布.在室内定位、水声导航、机动目标跟踪、电力系统等应用中[5-8],经常会出现受到大量野值、干扰等引起传感器具有厚尾特性非高斯噪声的情况.直接使用这些针对高斯噪声设计的滤波方法会导致估计精度下降甚至算法发散[8].

针对非高斯噪声系统状态估计的经典方法包括利用蒙特卡洛思想的粒子滤波和基于有限高斯分布逼近非高斯噪声的高斯求和滤波算法[6],由于计算复杂度高,限制了两者使用范围.近年来,针对非高斯噪声系统状态估计算法的研究主要包括基于距离[9]和基于分布[10]两种思路[11].基于距离的方法包括基于极大相关熵的滤波算法[12]、基于最小误差熵的滤波算法[5,13]、基于M 估计的滤波算法[9]、基于统计相似度的鲁棒滤波方法[14-15]等.以基于极大相关熵的滤波算法为例,此类方法利用相关熵概念替代常用的二范数形式来定义代价函数,据此求解得到针对线性系统[12]、非线性系统[16-18]和传感器网络系统[19]的各类滤波算法.此类算法不针对特定类型的非高斯分布,但是其抑制非高斯噪声的能力与核宽度有关,且缺乏严格的自适应更新依据,其估计精度提升有限.与之类似,基于最小误差熵和基于M估计的滤波算法均有对估计性能影响显著的参数需要调整,基于统计相似度的滤波方法需要考虑相似度函数选择的问题.第二种思路是采用典型的分布来建模常见的厚尾非高斯噪声,常用的有学生t 分布[20-22]、多变量Laplace 分布[11,23]、椭球分布[24-25]等,一般是利用此类分布的高斯尺度混合表达形式借助变分贝叶斯等方法得到后验估计.

根据中心极限定理,常见传感器的噪声可以建模为高斯分布,且在工程实践中一般能满足需求.但是在特定的场景下传感器不可避免面临各种异常扰动、使用环境变化等引起噪声分布发生改变.以基于传感器网络的目标跟踪为例,在开阔的理想场景下,传感器噪声建模为高斯分布是合适的;当目标进入室内、森林、地下等复杂场景,在传感器和目标之间存在干扰、遮挡、折射、多路径等情况下传感器测量误差会增大,存在大量异常噪声,此时可以建模为厚尾非高斯分布;当目标再次进入空旷的环境中,则可以继续利用高斯噪声假设.能够适应这种非平稳厚尾非高斯噪声的鲁棒状态估计算法更具有一般的实用价值.现有的鲁棒状态估计算法理论上能够适应这种变化,但是很难在两种情况下均取得较好的估计效果.针对线性系统,文献[26]和文献[27]考虑将这种噪声建模为高斯-学生t 混合分布,文献[28]进一步考虑了噪声存在偏态的情形,但是其混合函数的精确后验分布没有给出.针对非线性系统,文献[29]中采用了高斯分布和学生t 分布来混合建模非平稳厚尾量测噪声,利用UKF 计算非线性积分项,但是算法没有考虑量测噪声矩阵的变化,表征高斯分布和厚尾噪声的切换参数也缺乏自适应更新策略.

针对现有方法存在的问题,需要选择适当的分布保证其既能建模不同厚尾程度的非高斯噪声又能精确得到其后验参数概率密度函数.此外还需要解决如何自适应更新噪声参数以及切换参数的问题.考虑到多种常见厚尾分布为广义双曲分布特例且其尺度混合函数为共轭分布的特性[30-32],本文基于广义双曲分布构建高斯-广义双曲混合分布来研究带非平稳厚尾量测噪声的非线性系统状态估计问题,通过对超参数选择合适的先验分布并借助变分贝叶斯学习实现参数的自适应更新.本文主要贡献包括:1) 通过引入伯努利变量构建高斯-广义双曲混合分布建模非平稳厚尾噪声,利用广义双曲分布的高斯分层形式建立系统的概率形式模型;2) 选取合适的先验分布,利用变分贝叶斯方法实现系统状态、噪声参数以及切换参数后验分布的联合估计,建立了此类问题的估计框架,现有的几种鲁棒滤波算法[22-23,29]均是其特例;3) 基于传感器网络的机器人目标跟踪仿真实验表明,本文所提算法与现有方法相比有更好的估计精度和数值稳定性.

1 问题描述

考虑如下一般的非线性加性噪声系统

其中,xi ∈Rm表示系统在i时刻的状态向量,过程噪声wi ∈Rm是均值为零、方差为Qi的白噪声,zi ∈Rn表示传感器在i时刻的量测数据,状态转移函数fi(·) 和量测函数hi(·) 为维数适当的已知非线性函数,量测噪声vi是均值为零、方差为Ri的白噪声,且与过程噪声wi不相关.当过程噪声和量测噪声均服从高斯分布时,(1)和(2)可以表示为条件概率形式[29]

其中,p(·)表示概率密度函数.本文考虑量测噪声为非平稳厚尾噪声时的状态估计问题,即量测噪声在厚尾非高斯噪声和高斯噪声之间切换.在利用高斯-广义双曲混合分布建模此类噪声的基础上,进而利用变分贝叶斯的方法求解状态和参数后验估计,建立此类问题的卡尔曼滤波算法框架.

2 高斯-广义双曲混合分布

本节首先介绍双曲分布,用来建模一般的厚尾非高斯噪声;进而构建高斯-广义双曲混合分布建模这类在高斯噪声和厚尾噪声之间切换的非平稳厚尾量测噪声.

2.1 广义双曲分布

如果一个变量y∈Rny服从广义双曲分布,则其概率密度函数可以表示为如下形式[30-31]

其中,µ是与变量y同维度的向量,P∈Rny×ny为正定矩阵,混合函数p(τ) 服从广义逆高斯分布GIG(τ;δ,ω,η),其参数取值以及详细特性在附录A 中给出,逆高斯分布、伽玛分布和逆伽玛分布均是其特例.

此外,p(y|τ) 是均值为 (µ+τγ)、方差为τP的高斯分布,即

由上式可以建立广义双曲分布与高斯分布的联系.

广义双曲分布可以借助 (µ+τγ) 建模偏态特性,本文为简单起见,仅考虑µ=0 且γ=0 的零均值无偏态的情景,此时广义双曲分布记作GH(y;δ,ω,η,P).本文提出的算法框架也很容易扩展到噪声存在偏态的情形.

p(y) 分布特性取决于其混合函数p(τ). 当p(τ)取不同的参数时,广义双曲分布将退化成多种常见分布.除高斯分布外,还包括正态逆高斯分布、双曲分布、K 分布 (又称广义Lapalce 分布)、广义双曲学生t 分布 (常见的学生t 分布是其特例) 等多种具有厚尾特性的分布 (详见表1)[30-32].当参数δ,ω和η变化时,广义双曲分布的概率密度函数形状可以参阅文献[31].可以发现其形状对于参数δ最为敏感,选取适当的参数该分布能表征各种不同厚尾程度的非高斯噪声.基于广义双曲分布建模所得到的结果适用于一系列的厚尾分布噪声,结果具有普适性.

表1 广义双曲分布的几种特殊分布Table 1 Several special cases of generalized hyperbolic distribution

2.2 高斯-广义双曲混合分布

为建模非平稳厚尾量测噪声,引入辅助变量si,量测噪声则可以表示为如下高斯-广义双曲混合分布形式

其中,si ∈{0, 1}. 当si=1 时,表示量测噪声服从典型的高斯分布;当si=0 时,表示量测噪声服从广义双曲分布,用来建模大量的尖峰脉冲干扰等诱导的厚尾类型非高斯噪声.采用此建模形式,可以很方便地在高斯分布与厚尾非高斯噪声之间实现切换.

由于si ∈{0, 1}是离散的二值变量,因此可以利用参数为λi的伯努利分布来建模[26-27],其概率质量函数可以表示为

伯努利分布参数λi的共轭先验为贝塔分布[23]

其中,0＜κ0＜1 和 1-κ0为贝塔分布的参数.

根据广义双曲分布的特性,其混合函数τi服从广义逆高斯分布

进一步考虑量测噪声矩阵Ri存在不确定性,对于这种正定矩阵常用逆威沙特分布来建模[3]

其中,v0和V0分别为自由度参数和逆尺度矩阵.

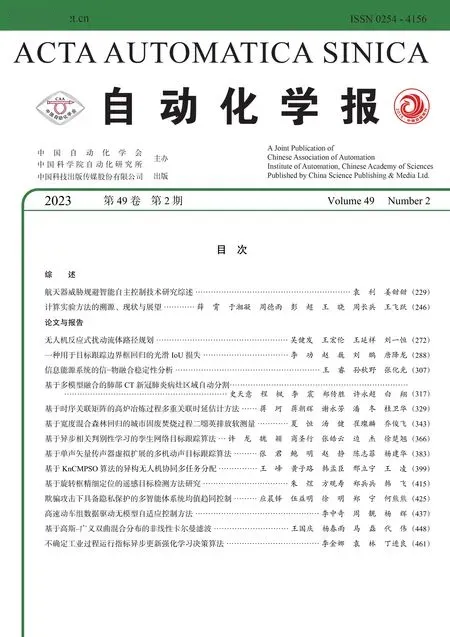
综上所述,(3) 和 (7) 分别是本文所研究系统概率形式的状态方程和量测方程.为便于理解,图1中给出了相应变量关系的图模型.

图1 本文系统的图模型Fig.1 Graph model of the system used in this paper

3 本文提出的算法

为得到递推的状态估计算法,首先假设上一时刻的状态后验为高斯分布p(xi-1|Zi-1)=N(xi-1;其中为i-1 时刻状态估计值,Pi-1|i-1为误差协方差矩阵,Zi-1={z1,z2,···,zi-1}表示量测数据的集合.算法初始化时假设已知状态均值和误差协方差矩阵P0|0.接下来将利用模型信息和i时刻的量测信息zi设法求得当前i时刻后验估计与常规卡尔曼滤波算法一致,算法也包括预测更新和量测更新两步.

3.1 预测更新

由于上一时刻状态后验为高斯分布,考虑到系统噪声也服从高斯分布,则算法的时间更新与常规的非线性估计方法一致.状态一步预测的概率密度函数表示为[23,29]

其中,状态一步预测可以通过下式得到

其误差协方差矩阵Pi|i-1为

3.2 量测更新

根据贝叶斯公式,系统状态以及未知参数后验估计可以根据下式求得

其中,Θi={xi,Ri,τi,si,λi}.由于量测噪声不再服从高斯分布且未知变量之间存在耦合,上式解析解不存在,不能直接进行求解.

针对系统状态与参数联合估计问题,常用的方法有EM 算法和变分贝叶斯方法,其中变分贝叶斯方法能适应隐变量维数更高的状态估计问题,且能够得到更好的估计结果[1],也是EM 算法和极大后验估计的推广[31].因此本文借助变分贝叶斯方法进行求解,将联合后验分布近似为每个变量后验分布的乘积[1,3]

其中,q(·) 表示变量的后验概率密度函数或者概率质量函数.

每个变量后验分布通过最小化其与真实后验之间的Kullback-Leibler 散度 (Kullback-Leibler divergence,KLD) 来求解

根据变分贝叶斯框架,上式的最优解为[3,23,31]

其中,ϑ表示集合 Θi中的任意一个元素,Θ-iϑ表示集合中除ϑ以外其他元素的集合,E (·) 表示期望,cϑ表示与ϑ有关的常数,l n(·) 表示对数运算.

根据系统概率模型,结合贝叶斯公式和条件概率公式,联合概率密度函数p(Θi,Zi) 可以分解为以下乘积形式

代入相关分布的概率密度函数表达式,可以得到(19)的对数形式

其中,t r(·) 表示矩阵的迹,|·| 表示行列式.

借助 (18) 和 (20),可以利用变分贝叶斯迭代分别求解各个未知变量的后验分布.接下来将给出各个变量具体的后验分布形式以及参数计算方法.

3.2.1 状态变量 xi 的后验分布

根据 (18) 和 (20),令ϑ=xi,合并与变量xi有关的参数,其余待求解变量用其上一次迭代的期望替代,可以得到状态xi后验分布的对数表达式

其中,上标 (l) 表示第l次固定点迭代,cxi表示与xi相关的常数 (下同).

整理可得

其中,量测预测值与常规非线性滤波方法一致,即

3.2.2 变量 R i 的后验分布

令ϑ=Ri,利用 (18) 和 (20) 可以得到

根据后验分布的对数形式,可以看出其依然为逆威沙特分布.通过参数匹配可以得到变量Ri的后验分布为

利用威沙特分布的均值特性,可以得到如下期望[3]

3.2.3 变量 τi 的后验分布

令ϑ=τi,代入 (18) 和 (20),可以得到

由于广义逆高斯分布为共轭分布[30-31],通过匹配参数,可以发现其后验分布依然为广义逆高斯分布,即

相应的参数分别为

3.2.4 变量 si 的后验分布

令ϑ=si,根据 (18) 和 (20) 有

根据 l nq(l+1)(si) 的形式,可以发现si的后验分布依然服从伯努利分布,其后验概率质量函数表示为

利用伯努利分布的特性,si的期望为

3.2.5 变量 λi 的后验分布

令ϑ=λi,根据 (18) 和 (20) 可得

匹配后验分布,可以发现λi依然为贝塔分布,即

其中,ψ(·) 表示双伽玛函数.以上期望用于 (47) 和(48) 的计算.

至此,已经得到所有未知参数的后验分布以及参数计算方法,完整算法将在第 3.3 节给出.

3.3 算法流程

本文提出的基于高斯-广义双曲混合分布的非线性卡尔曼滤波算法在i时刻完整的步骤如下:

步骤 1.输入参数:v0,δ0,ω0,η0,κ0;

步骤 2.预测更新: 根据 (13) 和 (14) 计算和Pi|i-1;

步骤 3.量测更新:

1) 迭代初始化:

算法利用双曲分布建模厚尾非高斯噪声,通过引入二值变量si来表征系统在高斯噪声和厚尾噪声之间的切换.由于双曲分布的混合概率密度函数τi为共轭的广义逆高斯分布,τi的后验估计是封闭的,利用精确的后验密度得到的估计结果更为准确.此外算法考虑了Ri,si和λi的自适应更新,算法的鲁棒性更好.算法中存在多处非线性积分项,可以利用无迹变换、容积变换等基于有限采样点的方式来计算[3],或者借助一阶泰勒展开的思路计算非线性积分的均值和方差信息[16].换而言之,本文算法的具体实现可以借助EKF、UKF 等常规非线性滤波算法中处理非线性的方法来处理非线性.本文算法显然也适用于线性系统.

另一方面,由于利用广义双曲分布建模厚尾噪声,现有常用的几种厚尾分布均是其特例,此外本文算法还考虑了参数的自适应估计,因此现有的几种常见的鲁棒滤波和自适应滤波算法均是本文算法的特例.具体而言,在si=1 条件下,取η0=0,δ0＜0,ω0＞0,且δ0=-ω0,则本文提出的算法退化为文献[22]中基于学生t 分布建模非高斯量测噪声的鲁棒滤波算法;当ω0=0,η0=1,δ0=1 时,则双曲分布退化为多变量Laplcae 分布,本文提出的算法退化为文献[23]中基于多变量Laplace 分布的RSEML 滤波算法.当si=0,本文算法退化为文献[33]中高斯噪声下自适应估计量测噪声的VBAKF-R算法.文献[29]中基于切换思想的SMKF 算法是本文算法中si=0.5,η0=0,δ0＜0,ω0＞0,Ri为固定值的一种特例.

所提算法的计算量主要受固定点迭代次数N影响,后面的仿真实验可以看到仅需要几次迭代即可收敛,因此算法的计算量相对经典CKF 和UKF算法增加较少.本文算法中参数v0和V0可以参考文 献[23] 设 为v0=ρ和其中常数ρ ＞为量测噪声主导方差矩阵.后文仿真结果表明,由于算法能够自适应调整噪声参数的后验估计,在一定范围内本文所提算法对于初始参数具有较好的鲁棒性,具体而言,算法对于δ0,ω0和η0的初始值具有一定的鲁棒性,对于参数κ0和E(0)(si)不敏感.实际使用时,可以按照表1 中典型分布选取δ0,ω0和η0的值,其余参数可以参考后文的仿真效果选取.

4 仿真实验

4.1 仿真设置

为验证本文所提算法的有效性和优越性,下面以一个二维平面内目标跟踪的例子来比较本文算法与同类算法的估计性能,并考察算法参数对估计效果的影响.

考虑利用3 个测距传感器 (如超声波传感器、UWB 模块等) 跟踪一个机器人的场景 (如图2 所示)[19,34].

图2 基于传感器网络的机器人跟踪示意图Fig.2 The illustration of tracking a robot with the sensor network

二维平面内跟踪问题的系统方程表示为[19,23]

其中,取q=10.

量测方程为目标到3 个传感器的测距信息,即[19,23,34]

其 中,(x(1)=0 m,y(1)=0 m),(x(2)=1 000 m,y(2)=0 m),(x(3)=0 m,y(3)=1 000 m) 分别为传感器的坐标.

为便于比较不同算法的估计效果,定义常用的位置和速度的均方误差 (Root mean square error,RMSE) 来度量估计误差.以位置RMSE 为例,其定义为[19,22-23]

其中,上标s表示第s次蒙特卡洛仿真实验,为i时刻真实的位置,表示i时刻滤波算法的估计结果,M=500 是蒙特卡洛仿真的总实验次数,R MSEvel的定义也类似.

为公平起见,各类算法中的非线性积分项均采用容积规则 (一种特殊的无迹变换,故部分对比算法后缀用UKF 结尾) 来计算.需要变分贝叶斯迭代的算法默认迭代次数N=10,仿真时长设为 4 00 s.与同类算法[19,23,26-28]类似,量测噪声按照如下方式生成

其中,w1,i～U(10, 100) 表示服从 [ 10, 100] 之间连续的均匀分布;w2,i=1+0.5 cos(πi) 用来建模噪声方差矩阵时变; w.p.表示出现概率;R0=diag{100 m2, 50 m2, 200 m2}.后续仿真中量测噪声主导方差矩阵设为即在 [ 0 s, 300 s] 内模拟典型的厚尾非高斯噪声,量测噪声70%概率为 N (0,w2,iR0),30%概率为N(0,w1,iR0). 在 (300 s, 400 s] 内量测噪声服从参数时变的高斯分布 N (0,w2,iR0).为便于理解,以一维情况为例,图3 中给出了噪声的幅值序列以及各段的概率密度函数,其中 [ 0 s, 300 s] 为厚尾分布,(300 s, 400 s]为高斯分布,[ 0 s, 400 s] 为非平稳厚尾分布.可以看到,尽管非平稳噪声的幅值发生较为明显的变化,但是概率密度函数变化不明显,本文算法考虑到此种噪声分布的切换,能够得到更好的估计效果.

图3 仿真中产生一维噪声的幅值以及概率密度函数Fig.3 The amplitude and probability density functions of the one-dimensional noise used in the simulation

4.2 算法对比

接下来比较本文提出算法与同类算法的估计精度.实验中对比以下10 种算法: 现有的6 种算法,包括利用量测噪声主导方差矩阵的经典UKF 算法、文献[22]中的STUKF 算法、文献[18]中的MCUKF算法、文献[23]中的RSE-ML 算法、文献[29]中的SEUKF 算法、利用真实量测噪声方差矩阵的最优UKF 算法 (OUKF);本文提出算法的4 种典型特例,即算法中广义双曲分布分别为正态逆高斯分布(δ0=-0.5,ω0=2,η0=2,记作G-GHUKF1)、双曲分布 (δ0=1,ω0=2,η0=2,记作G-GHUKF2)、K 分布 (δ0=2,ω0=0,η0=2,记作G-GHUKF3)和广义双曲学生t 分布 (δ0=-2,ω0=2,η0=0,记作G-GHUKF4).STUKF 算法中先验参数设置为exp(-5); RSE-ML 算法中ρ2=5;MCUKF 算法中核宽度σ=8; SEUKF 算法中选择a0=2,b0=2,λ0=0.5(为比较更为公平,逆伽玛分布的先验信息与本文算法选取一致);本文提出的几种算法中设置为比较不同算法的计算复杂度,本节还给出了不同算法总的运行时间.仿真采用MATLAB R2020b 软件进行,所用的台式机电脑CPU 型号为英特尔酷睿i9-10900,主频为2.80 GHz,内存为16 GB.

仿真结果在图4 和图5 中给出.利用噪声主导方差信息的UKF 在量测噪声为非高斯噪声时估计误差比高斯噪声时显著增大,因此在实际使用中当非高斯噪声严重时必须予以考虑.现有MCUKF 在非高斯噪声时能够显著改善UKF 的估计精度,在噪声恢复为参数时变的高斯噪声时其估计效果依然较好,但是由于该算法没有充分利用噪声统计特性,且其核宽度难以自适应更新,其估计精度还有提升空间.STUKF 算法和RSE-ML 算法分别采用了学生t 分布和多变量Laplace 分布来建模厚尾非高斯噪声,两者在非高斯噪声情况下估计精度较好,但是在噪声切换到正常的高斯噪声时,算法估计精度相对较差.SEUKF 算法建模中考虑了噪声切换,但是由于其不能自适应更新量测噪声方差矩阵以及噪声切换信息,在本文的场景下容易出现数值计算错误,图中仅给出了前51 s 的误差曲线 (后续部分由于频繁出现数值计算不稳定,软件自动剔除).本文所提算法的4 种特例在非高斯噪声情况和高斯噪声下均能够得到较好的估计精度,特别是在由非高斯噪声切换到参数时变的高斯噪声后,算法能够自动适应这种分布变化,精度显著高于同类的STUKF和RSE-ML 算法,体现所提算法的优越性.此外本文所提的算法当双曲分布参数选为4 类不同的具体分布时,估计精度相差不大.

图4 本文所提算法与同类方法的RMSEposFig.4 The R MSEpos of the proposed algorithms and related ones

图5 本文所提算法与同类方法的RMSEvelFig.5 The R MSEvel of the proposed algorithms and related ones

根据表2 中不同算法的计算时间来看,本文所提算法计算耗时与同类基于变分贝叶斯的方法处于同一量级.由于每个采样时刻进行了10 次固定点迭代,因此本文算法计算耗时大约是经典UKF 的10 倍,后续仿真可知利用更少的迭代次数依然能够得到较好的估计效果,相应的计算耗时也会随之减小.另外G-GHUKF4 中由于参数选择的原因,后验分布不需要计算第二类修正贝塞尔函数,因此计算量相比其他几种情况稍低.

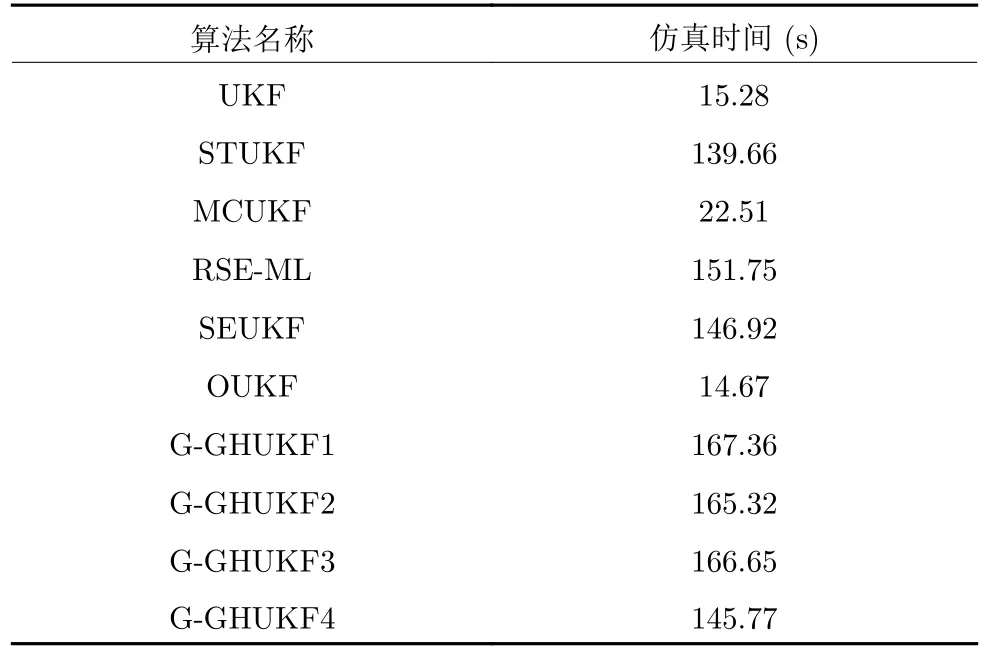
表2 不同算法总运行时间Table 2 The total simulation time of different algorithms

4.3 算法参数选择

接下来将详细探讨本文所提算法参数对于估计效果的影响.

首先,考察变分贝叶斯迭代次数对于估计精度的影响.固定其他参数 (δ0=1,ω0=2,η0=2),迭代次数N分别取3、6、9、12、15,估计结果在图6和图7 中给出.可以看到当N≥6 时估计误差重合,即算法仅需要几次就可以收敛,估计精度不再提高,因此变分贝叶斯迭代带来的计算负担较小.

图6 本文算法在迭代次数 N 不同时的RMSEposFig.6 The R MSEpos of the proposed algorithms with different iteration numberN

图7 本文算法在迭代次数 N 不同时的RMSEvelFig.7 The R MSEvel of the proposed algorithms with different iteration numberN

其次,固定δ0=-0.5,令ω0=η0分别取1、2、3、4、5,仿真结果在图8 和图9 中给出.图中可以看到,当两者参数过小 (均为1) 时估计精度略微降低,两者参数设置更大时估计结果基本不变.

图8 本文算法在 ω0 和 η0 不同时的RMSEposFig.8 The R MSEpos of the proposed algorithms with different ω0 andη0

图9 本文算法在 ω0 和 η0 不同时的RMSEvelFig.9 The R MSEvel of the proposed algorithms with different ω0 andη0

随后,固定ω0=2 和η0=0,δ0分别取-2、-3、-4、-5、-6,估计误差在图10 和图11 中给出,可以看到当δ0过大时估计精度会略微下降.

图10 本文算法在 δ0 不同时的RMSEposFig.10 The R MSEpos of the proposed algorithms with different δ0

图11 本文算法在 δ0 不同时的RMSEvelFig.11 The R MSEvel of the proposed algorithms with different δ0

最后,还考察了 E(0)(si) 和κ0对算法估计结果的影响,改变两者取值对于估计基本没有影响,因此不再给出其仿真结果.

5 结论

针对带非平稳厚尾量测噪声非线性系统的状态估计问题,本文引入高斯-广义双曲混合分布进行噪声建模,利用变分贝叶斯方法求解其状态以及各种噪声参数的后验分布,得到了基于高斯-广义双曲混合分布的非线性卡尔曼滤波算法框架.分析表明,现有的几种鲁棒 (自适应) 滤波算法均是其特例,且本文提出的算法框架相比现有方法具有更好的估计精度和数值稳定性.未来的研究方向包括考虑量测噪声存在偏态、系统噪声也存在非平稳厚尾噪声、分布式的多传感器信息融合等复杂场景.

附录A.广义逆高斯分布及其特性

广义逆高斯分布GIG(τ;δ,ω,η) 的概率密度函数为[30-31]

可以看到这是一种三参数连续型分布,其参数选取需要满足[30]:当δ<0 时,ω >0,η≥0; 当δ=0 时,ω >0,η>0; 当δ >0时,ω≥0,η>0.

常见的逆高斯分布、伽玛分布和逆伽玛分布分别是广义逆高斯分布取δ=-0.5,ω=0 和η=0 时的特例.对于一般的广义逆高斯分布p(τ) 而言,当ω>0 且η>0 时,其r阶原点矩可以表示为[30-31]

当ω=0 或η=0 时,上式不再适用,此时p(τ) 分别退化为伽玛分布和逆伽玛分布[30-31].

当η=0,δ<0,ω>0 时,广义逆高斯分布退化为逆伽玛分布,即

其中,伽玛分布的两个参数分别为形状参数和尺度参数.当τ服从伽玛分布时,则τ-1服从相同形状参数和尺度参数的逆伽玛分布.由此可以得到本文中用到的τ和τ-1的期望分别为(δ/=-1)

当ω=0,η>0,δ>0 时,广义逆高斯分布退化为伽玛分布,即

则可以得到(δ/=1)