基于KnCMPSO算法的异构无人机协同多任务分配

王 峰 黄子路 韩孟臣 邢立宁 王 凌

无人机(Unmanned aerial vehicle,UAV)以其体积轻巧、隐身性能好、续航时间长、可回收重复使用等优势逐渐成为空中作战的主角.相较于有人机,无人机能够在偏远、危险或者人员不可达的极端环境中,自主完成一些重要的诸如监测、搜救、侦察、打击等任务[1].无人机协同作战是指在实际的战场中,多种类型的无人机充分发挥各自优势,协同完成一项军事任务.早期的无人机协同作战由于作战场景简单、任务类型单一、任务难度较低,仅通过人工决策就能确定各无人机的作战序列.然而随着作战场景逐渐复杂、任务类型逐渐多样化、无人机智能化水平逐渐提高,仅靠人工决策很难充分挖掘各种无人机的特性并发挥无人机系统的协同作战优势.现实世界中的无人机往往是异构的,异构无人机指的是多种类型的无人机(侦察机、战斗机等)[2],为了提高异构无人机执行任务的效率,提升异构无人机系统的自主性,开展异构无人机协同多任务分配问题研究具有十分重要的意义[3].

为了高效地制定无人机的任务分配计划、科学地控制无人机,需要对无人机协同多任务分配问题建立合适模型.

在模型的约束条件研究方面,文献[4]充分考虑了无人机执行任务之间的时序和多机协同等约束条件,将无人机分配问题构建成为协同多任务分配问题模型.文献[5]提出以无人机自身性能约束、协同约束和实际三维复杂环境构建约束的无人机任务分配模型.然而上述模型中所考虑的各无人机都具有侦察、打击、评估三种能力,不属于异构无人机.在实际问题中,由于不同无人机的能力有差异,无法用一类无人机完成所有任务.因此通常选择采用多架异构无人机组成集群来共同完成任务,解决不同无人机的能力限制.一些学者进一步对异构无人机协同任务分配模型提出了新的约束条件,如文献[6]考虑无人机资源消耗、完成任务资源需求等约束,文献[7]考虑任务优先级等约束,文献[8]考虑无人机运动学等约束.

在模型的优化目标研究方面,目前大部分研究工作建立的都是以最小化无人机飞行距离的单目标模型[9],也有一些学者尝试构建无人机任务分配的多目标优化模型.如文献[10]提出同时考虑无人机任务收益、任务执行时间和任务执行代价的多目标模型,文献[11]以无人机总飞行距离和任务完成时间为优化目标构建了多目标优化模型.

在无人机协同多任务分配模型的求解方面,近年来也有部分学者进行了深入研究[12],其中粒子群算法[13]作为群智能算法中的经典算法,具有操作简单、收敛能力强等特点,可以很好地求解无人机协同任务分配问题.文献[14]将多种目标函数进行加权,利用离散粒子群算法对构建的模型进行求解,但是采用的交叉变异操作方式较为简单,求解效率有待进一步提升.文献[10]利用多目标量子粒子群算法对无人机任务分配问题进行求解,但是算法编码较为复杂,计算量比较大.文献[15]提出采用改进的量子粒子群算法对无人机任务分配问题进行求解,但是算法需要额外计算平均历史最优位置而且设定的参数较多.近年来,随着异构无人机协同多任务分配模型研究的深入,一些学者针对异构无人机协同多任务分配问题的求解算法进行了探讨.如文献[11]提出一种基于协同进化的混合变量多目标粒子群优化算法,但其更新策略过于简单且随机性较大,随着问题规模的增大,求解效率将逐渐下降.文献[16]提出改进的多目标量子粒子群算法,但其重组方式较复杂,求解效率不高.文献[17]提出改进的遗传算法,但该算法主要针对单目标优化模型,无法很好地求解多目标异构无人机任务分配模型.

异构无人机协同多任务分配模型有多个复杂的约束条件,因此,如何处理不同类型的约束条件,以提高算法的搜索效率,是求解异构无人机协同多任务分配模型的重要问题.近年来,一些学者针对不同类型的应用问题,研究采用不同约束处理方法进行求解.求解方法大致可以分为基于罚函数(Prnalty function,PF)的约束处理方法[18-20]、基于可行性原则的约束处理方法(Stochastic ranking,SR)[21-22]、基于随机排序的约束处理方法 (Feasibility rule,FR)[23]和基于多目标的约束处理方法[24]4 类 .也有一些学者就约束处理技术理论方面提出了一些新的改进,如基于分级方式的约束处理准则[25]、基于集成方式的约束处理准则[26]或将约束转化为新的优化目标[27].而在异构无人机协同多任务分配模型中,存在无人机类型约束、任务执行时序约束及多机协同约束等多种复杂约束,上述方法无法直接用于求解.

为了使构建的模型更加符合现实场景,现有对无人机任务分配问题的研究工作均在约束条件或目标函数上对模型做出了改进,但是大部分研究工作均假设无人机的观测时间和一次弹药消耗都是充足的,然而在实际作战过程中,当侦察机一次观测时间过长时,存在被敌方发现乃至击毙的风险,战斗机一次发射的弹药数量也是有限的.因此本文在现有研究工作[11]的基础上,进一步考虑无人机单次任务最大观测时间约束和无人机单次任务最大弹药约束,建立基于多种约束条件的异构无人机协同多任务分配问题模型.

上述模型不仅包含混合变量,同时还存在多个复杂的约束条件,问题的求解难度较大,传统的多目标优化算法并不能有效地求解上述模型.同其他智能优化算法相比,粒子群算法具有计算简单、鲁棒性好、搜索能力强且收敛速度快的特点,在求解多约束多目标异构无人机协同任务分配问题时,具有较大优势.为了高效求解该模型,本文提出了一种基于拐点的协同多目标粒子群优化算法(Knee point based coevolution multi-objective particle swarm optimization,KnCMPSO).本文的主要贡献如下:

1)针对模型包含混合变量以及多种约束的特点,采用基于三维矩阵的混合编码方式以及基于约束处理的初始化方法,有效避免不可行解的生成,提高算法的搜索效率.

2)采用协同进化策略,将多目标优化问题转为多个单目标优化问题,通过子种群间合作式协同降低求解复杂度,通过子种群内竞争式协同进化加快算法收敛,进一步提出基于学习的粒子更新策略来提升算法的收敛性,粒子不仅学习父代优秀个体,也学习精英个体或全局最优个体,可以实现更快收敛.

3)提出基于区间扰动的局部搜索策略来提升算法的多样性,进一步提出基于拐点的学习策略来更新外部档案集,加强了算法对帕累托前沿中心面的搜索,在保证收敛性的同时提升算法的多样性,使得算法能搜索到更多的可行任务分配结果.

本文首先对无人机协同多任务分配问题建模,然后介绍基于拐点的协同多目标粒子群优化算法,接着设计仿真实例来验证算法的有效性,最后进行总结和展望.

1 异构无人机协同多任务分配模型

1.1 问题描述

表1 展示了模型中涉及的各种符号以及相应说明.

表1 符号说明Table 1 Symbol description

异构无人机协同多任务分配问题描述如下: 假设在某二维已知区域内发现了NT个敌方目标,则目标集合T可表示为T={T1,T2,···,TNT}.无人机系统需要对每个目标依次执行三种不同类型的任务,分别为观测、打击、打击结果评估,即三种任务之间存在时序关系.任务类型集合M可以表示为M={Observe,Attack,Evaluate},因此模型中需要调度的总任务数量NM的值为NM=3×NT.异构无人机系统中的无人机可以被分为侦察机和战斗机两种类型,其中用于执行观测和打击结果评估任务的侦察无人机有S架,执行打击任务的战斗无人机有A架,则无人机集合表示为U={U1,U2,···,US,US+1,···,US+A}.无人机执行不同的任务需要消耗一定的资源量.同一个目标上的相同任务可以由多台无人机协同完成.当所有目标上的所有任务执行完成,整个军事作战任务顺利完成.

1.2 目标函数

为了能够更加合理地对无人机任务分配的结果进行评估,本文的模型采用无人机总飞行距离和任务完成时间两个目标函数.无人机的总飞行距离为无人机系统中所有参与任务的无人机飞行距离之和,任务完成时间为整个作战任务中最后一个完成任务的无人机的总飞行时间.根据以上定义,本文模型的计算公式如下:

无人机航程和其消耗资源数紧密相关,无人机飞行总航程越短,代表无人机执行任务时消耗的资源越少.然而,飞行总航程最短并不一定能保证军事任务的完成时间最短.例如,一些无人机可能在同一目标上被分配较多的任务以满足所有无人机飞行总航程最短,而这会导致该无人机完成所有任务的时间变长,从而使得整个军事任务完成时间变长.因此,无人机飞行总航程和任务完成时间两个指标存在一定的冲突.

1.3 约束条件

为了能够对多台无人机协同完成同一项军事任务进行更有效的刻画,本文在文献[11]基础上,进一步考虑无人机单次任务最大观测时间约束和无人机单次任务最大弹药约束来建立异构无人机多任务分配模型,其所包含的约束条件如下.

1)无人机类型约束.由于无人机的异构性,不同类型的任务只能由特定类型的无人机完成.

式中,i表示无人机编号,j表示目标编号,k表示任务编号.当k∈{Observe,Evaluate}时,i ∈{1,2,···,S}; 当k ∈{Attack}时,i∈{S+1,···,S+A}.

2)任务执行时序约束.对于同一个目标,无人机系统要先对其执行观测任务,然后对其执行打击任务,最后才能够执行打击结果评估任务.因此对同一个目标上的三种任务需满足如下时序约束.

3)最大携带弹药数目约束.战斗无人机只能携带一定数目的弹药.因此战斗无人机执行打击任务消耗的弹药数要小于其最大携带弹药数目.

4)单次最大侦察时间.为了避免暴露时间过长以至于被敌方发现,侦察无人机在执行观测任务和打击结果评估任务时存在最大侦察时间.

5)单次最大发射弹药数.战斗无人机在执行对某一个目标上的打击任务时,由于自己性能的限制只能发射一定数量的弹药.

6)多机协同约束.为了保证军事任务顺利完成,针对不同目标的不同类型的任务需要分配给不同数量的无人机协同执行.其中对同一个目标的观测和打击结果评估任务至少需被一架侦察无人机执行,而打击任务需要分配给至少一架战斗无人机执行.

7)完成任务资源需求约束.执行相同任务的所有无人机资源消耗总量需要大于等于完成当前任务所需要的资源总量.

无人机执行观测任务和打击结果评估任务需要消耗一定的时间资源,所有执行同一任务的侦察无人机侦察总时间需要满足完成任务所需总时间.

无人机执行打击任务需要消耗一定的弹药资源,所有执行同一任务的战斗无人机消耗弹药数量需要满足完成任务所需总弹药数量.

8)最大航程约束.假设无人机i执行的任务序列为Mi=(M1,M2,···,Mm),Dis(Mk,Mk+1) 表示无人机执行第k个任务到第k+1 个任务的飞行距离,M axDisi表示无人机最大飞行距离,则有:

上述异构无人机协同多任务分配模型所包含的决策变量既有表示任务分配结果的离散变量,也有表示无人机资源消耗的离散和连续变量,这些混合变量导致问题解空间变得更加复杂,难以进行有效搜索.同时模型还包含多个复杂的约束条件,既有不等式约束,也有等式约束,这些约束条件进一步使得问题对应的解空间变得不规则,增加了算法搜索到可行解的难度.

由于现有的算法无法对本文提出的多约束多目标异构无人机协同多任务分配模型进行有效求解,本文提出一种基于拐点的协同多目标粒子群优化算法求解无人机协同多任务分配问题.

2 基于拐点的协同多目标粒子群算法

本文提出的基于拐点的协同多目标粒子群优化算法KnCMPSO,主要通过设计基于约束处理的初始化策略、协同进化策略、基于学习的粒子更新策略、基于区间扰动的局部搜索策略及基于拐点的外部档案集更新策略提升算法的求解性能.

算法流程如图1 所示.首先,采用子种群间合作、子种群内竞争的协同进化策略,将多目标优化问题转为各个目标维度上的单目标优化问题,降低了问题的求解复杂度;其次,在各个子种群内部,针对无人机协同多任务分配问题包含混合变量以及多种约束的特点,以二进制交叉方法为基础,设计了基于学习的粒子更新策略和基于区间扰动的局部搜索策略,提升了算法的求解性能;最后,引入基于拐点的学习策略来更新外部档案集,增强了算法对帕累托前沿中心面的搜索,在保证收敛性的同时增强了算法的多样性.

图1 KnCMPSO 算法流程图Fig.1 Flowchart of KnCMPSO algorithm

2.1 编码以及初始化策略

在使用粒子群算法求解无人机协同多任务分配问题时,首先需要解决的问题就是如何对粒子中个体进行编码操作.为了处理模型中的混合变量以及各种约束条件,本文将采用基于三维矩阵的混合编码方式对决策变量进行编码.如表2 所示,编码矩阵中的第1 行是目标编号,每一个目标编号在粒子的第1 行都会出现3 次,按照出现先后顺序分别代表了在此目标上执行的观测任务、打击任务、打击结果评估任务.第2 行是无人机编号,代表了执行此任务的无人机.由于目标编号在矩阵出现的先后顺序代表了不同的任务类型,因此无人机编号(无人机类型) 需要根据目标编号所代表的任务类型来设置.第3 行是无人机执行对应任务的资源消耗,其中侦察机消耗的资源为时间,是连续变量,战斗机消耗的资源为弹药,是离散变量.

表2 粒子编码方式Table 2 Particle encoding scheme

基于三维矩阵的混合编码方式不但能够很好地描述目标、任务、执行任务的无人机以及无人机资源消耗的对应关系,而且能够直观地表示出各台无人机执行任务的先后顺序,方便后续初始化操作.虽然每个个体位置向量编码长度仍然可能不同,但是所有目标在编码中出现的次数是固定的,也就是说所有粒子的编码矩阵中第1 行目标编号的长度是固定的,这就大大降低了问题的求解难度.

在上述编码方式的基础上,本文提出基于约束处理的初始化策略,具体过程如算法1 所示.

表3 和表4 为初始化策略示例说明,表3 为目标队列集合,表4 为无人机集合.首先,建立一个4×N的目标矩阵,将所有的目标依次放入矩阵中的第1 行,每个目标上的任务按照观测任务、打击任务和打击结果评估任务的顺序依次排列到矩阵的第2、3、4 行.无人机按照侦察机和战斗机类别不同分别放入两个队列当中;然后,粒子将按照从左往右的顺序依次初始化位置向量.每次均从目标矩阵中随机选择一个目标,并将目标中尚未完成的任务取出进行分配.根据任务类型选择相应的无人机类型,并设置无人机对应的资源消耗.如果此任务上的所有无人机的资源消耗量与完成此任务的资源需求量相等则代表当前任务执行完毕.当某个目标对应的三种任务全部执行完毕代表此目标的分配全部完成;最后,当所有的目标都分配完成之后,得到的粒子就是一个满足所有约束条件的可行解,且可以有效避免出现由于某个任务的前置任务未完成而导致的死锁状态[28].

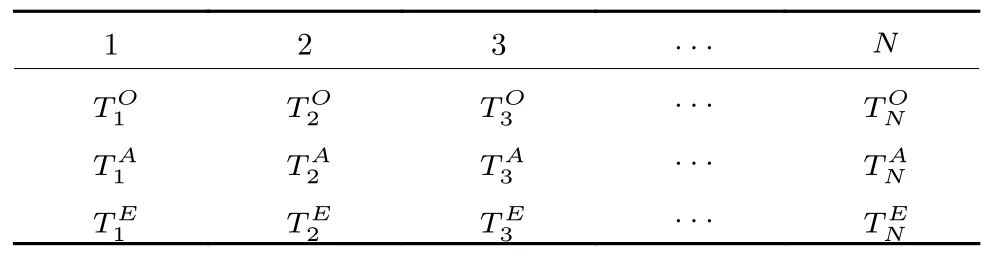
表3 目标队列集合Table 3 Target formation collection

表4 无人机集合Table 4 Drone collection

算法1.基于约束处理的初始化策略

2.2 协同进化策略

协同进化是生物学中一种重要的进化机制 , 可促进物种之间的信息交流并提高物种进化效率.协同进化策略包括了合作式协同进化策略和竞争式协同进化策略两种类型[29].已有研究表明,在优化算法中采用协同进化策略能够降低问题的求解难度,加快算法的搜索效率,提升算法的性能[30].

KnCMPSO 算法采用了子种群间合作式协同进化、子种群内竞争式协同进化的策略来生成新个体.子种群合作式协同进化采用子问题与子种群一一对应的方式,将多目标优化问题转为每一个维度上的单目标优化问题.子种群内竞争式协同进化则采用子种群内的全局最优个体和外部档案集中的精英个体相互竞争的方式来选择较优的个体,并利用该个体对子种群生成过程进行引导,避免种群向极端点靠近.其整体流程如图2 所示.针对一个M维的多目标优化问题,算法生成M个子种群,每个子种群分别针对每一个维度上的目标进行优化.同时利用外部档案集Archive 的方式保存迭代过程中寻找到的所有种群的非支配解,从而实现种群之间搜索信息的共享.

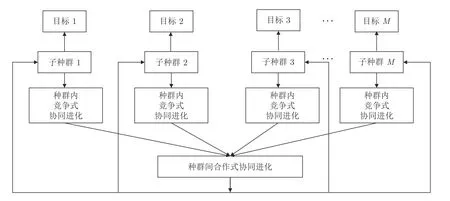
图2 种群间合作种群内竞争的协同进化策略Fig.2 Coevolution strategy of inter-population cooperation and intra-population competition

子种群间合作式协同进化是指将原始问题分别看作某一个维度上的单目标优化问题,同时利用外部档案集保存迭代过程中的所有种群的非支配解.由于子问题与子种群一一对应,子种群平行且单独地进化,降低了问题的求解复杂度.在传统的多目标问题中,当两个个体互不支配的时候,无法确定哪一个更优,导致算法无法选择个体最优粒子和全局最优粒子对当前个体进行更新操作.采用子种群间合作式协同进化可以有效避免上述问题.每个子种群根据当前维度目标值的大小来进行个体最优和全局最优的选择,实现在该维度上的求解.子种群内竞争式协同进化是指通过各个子种群中的全局最优个体和外部档案集中的精英个体之间竞争,获取

对子种群中的其他个体的引导权,具体过程如算法2 所示.

算法2.基于竞争的个体更新策略

如图3 所示,假设子种群1 的优化目标为f1,Gbest为子种群1 在迭代次数为t时候全局最优个体,待更新的个体为S.首先,在外部档案集中随机选择一个精英个体A.计算个体A和S之间的余弦相似度;然后,与Gbest和S之间的余弦相似度进行比较.当A与S之间的余弦相似度更小时,说明个体A对个体S的引导能力更强,更有利于算法的收敛,因此选择A作为S的全局学习对象;反之,选择Gbest作为S的全局学习对象.

图3 竞争式协同进化策略Fig.3 Competitive coevolution strategy

上述两种协同进化策略不仅能降低问题的求解复杂度,而且能有效提高算法的收敛速度.

2.3 基于学习的粒子更新策略

在标准粒子群算法中,种群中的个体通过对个体最优粒子和全局最优个体进行学习来更新速度,再通过粒子的当前位置和速度来更新粒子的状态.本文模型中包含了混合变量,并且约束条件较多,按照标准粒子群的更新方式将很难生成满足约束的粒子,所以本文将对粒子的更新方式进行改进,不再使用粒子速度这一个概念,粒子在更新的时候只通过向优秀个体学习的方式来更新粒子的状态.基于此,在KnCMPSO 中提出了一种基于学习的粒子更新策略,具体过程如算法3 所示.

算法3.基于学习的粒子更新策略

图4 中的lS表示待学习的个体,cS表示当前个体,nS代表经过学习方式之后生成的新个体.整个学习过程如下: 首先,初始化一个空的个体nS.依次选择模型中的目标编号,以一定的概率选择当前目标编号进行学习操作.假设当前选中的目标编号为2,则将待学习个体位置向量第1 行与2 相等的三个位置上的值,按照其在lS位置向量中出现的先后次序依次插入到新个体nS位置向量的对应位置,同时将各个任务对应的无人机以及无人机资源消耗量插入到位置向量的对应位置.对目标编号进行一次遍历之后,新个体nS中非空位置保存的就是待学习个体lS的信息.然后,将原始个体cS中的目标、目标对应的无人机以及无人机资源使用量从左到右依次填入到新个体位置向量中的空位置,跳过新个体nS中已存在的目标.

图4 粒子向较优个体的学习过程Fig.4 The learning process of particles from better individuals

通过向优秀个体进行学习,粒子位置向量将按照式(11)进行更新.其中Xi(t) 代表粒子i在第t次迭代中的位置,Pbesti为粒子在第t次迭代中的个体最优值,A为外部档案集中的个体,Gbest为第t次迭代中的全局最优,w为权重系数,competition代表了粒子A和Gbest相互竞争,F代表了粒子向较优个体的学习过程.

2.4 基于区间扰动的局部搜索

如前所述,采用上述基于学习的粒子更新策略对种群中的个体进行更新能够有效地对问题空间进行搜索,但如果粒子在更新的时候只采用该策略对群体中较优的个体进行学习,会导致算法在迭代后期陷入局部最优.为了进一步提升种群的多样性以及算法的搜索能力,本文进一步提出了一种基于扰动的局部搜索策略,具体过程如算法4 所示.

算法4.基于区间扰动的局部搜索策略

具体实现方式见图5.图5 中cS代表当前个体,nS代表执行完局部搜索策略之后生成的新个体.按照一定的概率在个体cS上随机选择某一个目标上的某一个任务k.按照任务执行的时序约束找到任务k可插入的位置范围 [startPos,endPos].图5 中加下划线的方框表示随机选择的任务k,两个灰色背景方框的位置从左往右分别为startPos和endPos.在此范围内随机选择任务插入的位置insertPos. 将任务k插入位置向量中的insertPos.其余位置的任务依次插入到nS的[startPos,endPos]之中,并重新设置完成任务k的无人机以及相应的资源消耗.需要指出的是,任务类型应满足无人机作战类型约束,即该任务如果是观测和打击结果的评估任务,则只能选择侦察无人机集合中的无人机,否则选择战斗无人机集合中的无人机.此外,所选择的无人机仍需满足资源约束和最大航程约束.

图5 基于区间扰动的局部搜索策略Fig.5 Local search strategy based on interval disturbance

2.5 基于拐点的外部档案集更新策略

将原始问题看作各个目标维度上的单目标优化问题,虽然降低了问题的求解难度,但是由于各个子种群分别优化某一个目标,种群将会向每个目标维度上的极端点靠近.最后得到的非支配解集也将更多地分布在各个目标维度的附近,导致算法搜索不到帕累托面的中心部分,降低算法的多样性.如图6 所示,以两目标问题为例,其中矩形点为极端点,圆形点代表非支配解,三角形点为支配解,虚线框所在的区域为中心解集区域.可以明显看出,中心区域解集分布较少.这是由于每一个子种群的全局最优为对应目标维度的极端点,使得种群在不断迭代过程中大部分的解将向极端点靠近,导致最后生成的非支配解集多样性不足.

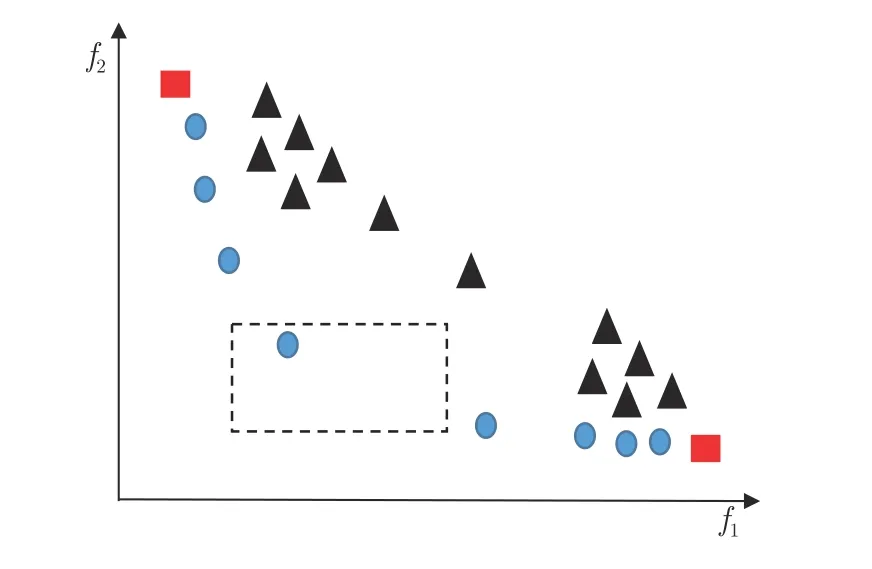
图6 解集分布不均匀图Fig.6 Uneven solution set distribution graph

为了使得外部档案集中的解集分布更加均匀,同时提升算法的收敛性,本文利用拐点来引导档案集中的其他精英个体的更新.如图7 所示,点B和点C为某个种群内部的边界点,两者之间的连线为L,通过计算种群中其他点到直线L的距离,选择距离最大的那个点作为拐点,即点A.对于三目标或者是超多目标问题,边界点所构成的是一个平面或是超平面,则拐点也被定义为距离这个平面或者是超平面最远的点.本文所提的利用拐点更新外部档案集的方式如式(12)所示,外部档案集中的个体向拐点学习更新位置向量.

图7 拐点图示Fig.7 Illustration of knee point

式(12)中Ai代表外部档案集Archive中任意的一个精英个体,kneePt代表拐点,F为粒子向优秀个体的学习过程,具体实现方式见第2.3 节.

3 实验与结果分析

本文基于不同的任务数量和无人机类型设计了4 种不同规模的实例并进行了仿真实验.实验中的算法均采用Java 编程,运行环境为JDK1.8,编译器为Eclipse,处理器为主频3.6 GHz 的Intel Core i7-4790.

3.1 仿真实例设计

本文设计了4 种不同规模的实例,其中实例1包含14 台无人机和6 个军事任务目标,实例2 包含16 台无人机和12 个军事任务目标,实例3 包含18 台无人机和18 个军事任务目标,实例4 包含20台无人机和24 个军事任务目标.各个实例中的任务目标被随机地设置在一个固定的位置,每一个任务目标上包含了三种属性,分别代表了完成此目标上的某一个军事任务所需要的资源量.各个实例中的无人机同样的被随机地设置在一个固定的位置,每一个无人机包括了飞行速度、最大携带弹药数目和最远飞行距离.实例4 中各个目标和无人机的属性设置情况如表5 和表6 所示,其他3 个实例见附录A.上述实例包含不同规模、不同分布的无人机任务分配场景,4 个实例的示意图如图8 所示.其中,实例1 和实例2 中的目标和无人机在军事区域内分布的相对集中且规模较小,这意味着在任务分配时可选择的合适的无人机较多,因此在实例1 和实例2 的目标空间中存在较多的局部最优解,算法在实例1 和实例2 上的实验结果能反映算法求解多峰优化问题时的性能.而实例3 和实例4 中目标和无人机的分布相对分散且规模更大,算法在实例3和实例4 上的实验结果能较好地反映算法求解模型的收敛性能.通过在4 个实例上做实验,可以对算法的探索能力和勘探能力进行较全面的评估.

图8 4 个实例的示意图Fig.8 Schematic diagram of four examples

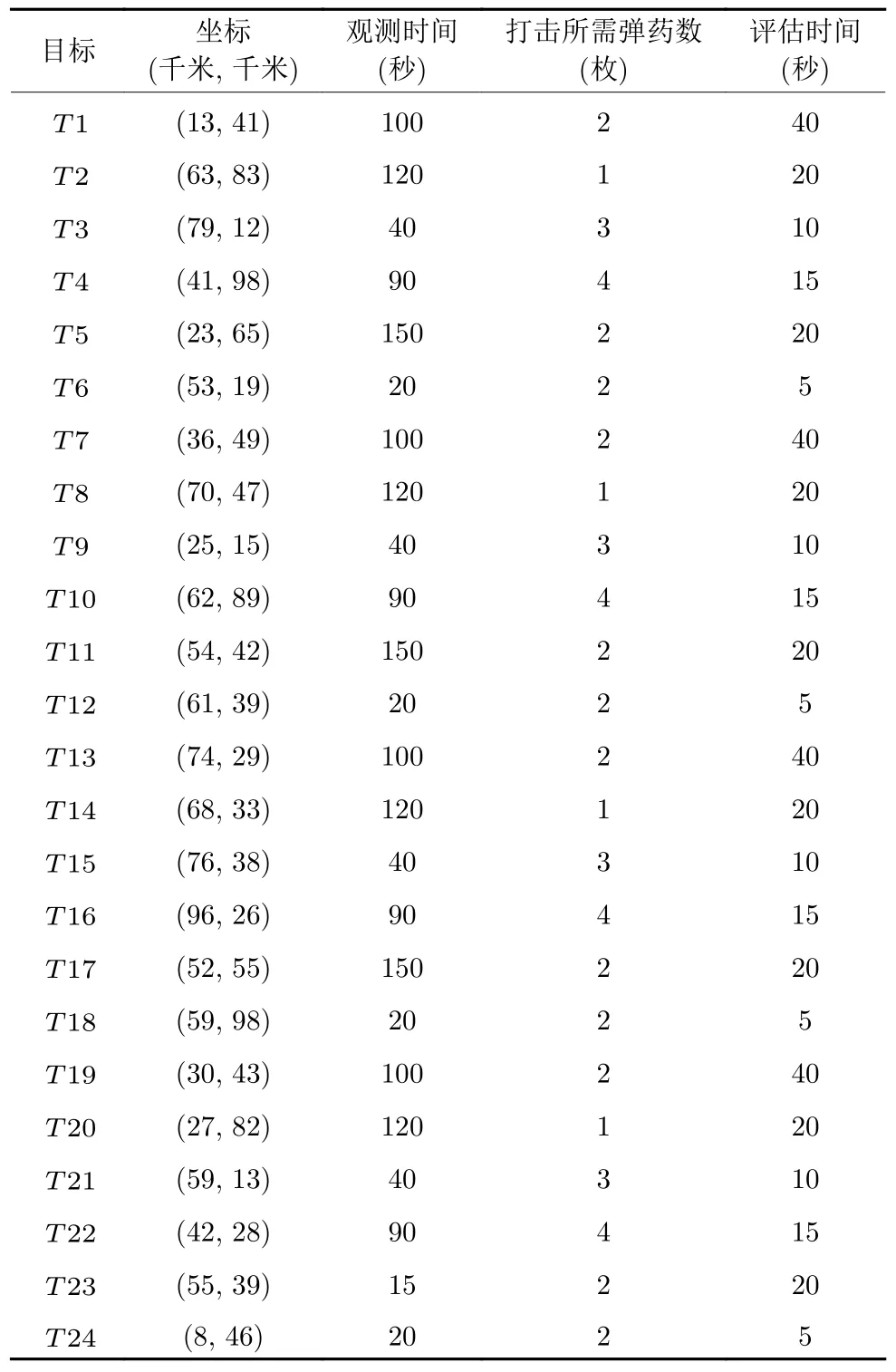
表5 实例4 中目标属性值Table 5 The target attribute value in example 4

表6 实例4 中无人机属性值Table 6 Attribute value of drone in example 4

其中军事任务目标和无人机的坐标单位为千米,无人机飞行速度单位为千米/秒,无人机最大飞机距离为2 000 千米.无人机完成观测任务和打击结果评估任务的最大观测时间为60 秒.无人机完成一次打击任务最大消耗弹药数量为4 枚.

3.2 对比算法和评价指标

为了验证KnCMPSO 算法性能,本文选取求解无人机协同任务分配问题的基于协同进化的混合变量多目标粒子群优化算法(Coevolution based mixed-variable multi-objective particle swarm optimization algorithm,C-MOPSO)[11]与3 个具有代表性的基于协同进化的多种群粒子群优化算法(Coevolutionary multiswarm particle swarm optimization,CMPSO)[30]、基于协同进化的粒子群优化算法(Coevolutionary particle swarm optimization,CPSO)[31]和基于分解的协同进化多目标局部搜索算法(Coevolutionary multiobjective local search based on decomposition,CoMOLS/D)[32]进行对比实验.所有算法的种群大小N设置为300,最大迭代次数为500 次,外部档案集大小均为种群大小的二分之一.同时采用超体积Hypervolum(HV) 指标评价各个算法获得非支配解集的优劣.HV 指标是一个综合性评价指标,能够同时评估算法在收敛性和多样性上的表现.HV 指标的数值越大,表示算法在收敛性和多样性上的表现越好.本文HV 指标参考点设置为(15 000,15 000).

3.3 实验结果与分析

为了使选取的各对比算法能够求解本文的模型,上述对比算法均采用了与KnCMPSO 相同的编码策略以及初始化方式.需要指出的是,为了保证实验结果的公平性,除C-MOPSO 算法之外,其他的算法均采用本文所提出的粒子更新方式和局部搜索策略.

在实验过程中,每个算法均将在上述无人机任务分配实例上执行30 次独立实验.各算法在所有实例上的HV 指标数据如表7 所示,其中Mean 表示各个算法30 次实验计算得到的HV 指标的平均值,其大小反映算法求得的非支配解集的收敛性和多样性.Std 表示各个算法30 次实验计算得到的HV 指标的方差,其大小反映算法的稳定性.Best表示算法运行30 次后得到的最优的HV 值.Worst表示算法得到的最差HV 值.表7 中各个测试函数上的最优结果加粗标注,次优结果用下划线标注.

表7 算法在各个实例上的HV 值Table 7 The HV value of the algorithm on each example

由表7 可以看出,相较于其他对比算法,Kn-CMPSO 在4 个实例上的HV 指标的平均值上都能取得最优结果,表明了算法在多样性和收敛性上均优于其他对比算法.另外KnCMPSO 算法求得HV 指标中Std、Best 和Worst 值相比较于其他对比算法同样是占优的,表明了KnCMPSO 算法在稳定性上同样优于其他对比算法.原因如下: 1) KnCMPSO 利用协同进化的策略降低了问题的求解难度;2) 通过引入基于拐点的外部档案集更新策略增加了算法对帕累托前沿中心区域的搜索能力.CMPSO 算法和CPSO 算法虽然同样采用了协同进化策略,但是在CMPSO 和CPSO 算法中极端点对个体的引导能力过于强烈,导致最后生成的解集更多分布在各个目标维度极端解的附近,算法的多样性受损.CoMOLS/D 算法采用的权重和法和反转边界交叉惩罚均是基于权重向量的策略.由于解集的好坏与权重向量的设置关系十分密切,在求解帕累托前沿分布不均匀的实际问题上优势不明显.C-MOPSO 算法针对无人机任务分配问题设计了基于结构学习的重组方法进行求解,但是这种重组方法不确定性较大,尤其是随着问题规模的不断变大,算法的求解性能逐渐降低,与C-MOPSO 算法的对比证明了本文所提粒子更新方式和局部搜索策略的有效性.

为了更加直观展示算法在各个实例上的结果分布情况,算法在每个实例上所得解集的分布情况如图9 所示.由图中各实例解集分布情况可以看出,相比较于其他对比算法,本文算法求解得到的解集不论是在多样性还是收敛性上都明显占优,这与上述HV 指标的评估结果一致.

图9 算法在各实例上的解集的分布图Fig.9 Distribution diagram of the solution set of the algorithm on each example

通过上述实验结果中本文算法和其他算法HV指标性能表现,以及5 个算法在各个实例中的解集分布情况可以发现,相比较于其他4 个算法,本文算法无论在收敛性方面还是多样性方面均明显占优,充分证明了本文算法求解无人机协同多任务分配问题的有效性.

为了验证KnCMPSO 算法所提基于学习的粒子更新策略的有效性,本文将文献[11]的基于结构学习的生成算子(Structure learning reproduction,SLR)嵌入到KnCMPSO 算法框架中,记该算法为KnCMPSO-SLR,与现有结果进行了对比,对比结果见表8.由表8 可以看出,KnCMPSO 在实例2上与KnCMPSO-SLR 的结果相近,但在实例1、实例3 和实例4 上都能取得最优结果,表明该算法可以保持较好的多样性和收敛性,其原因在于Kn-CMPSO-SLR 采用基于结构学习的粒子更新策略只学习了父代个体的部分基因,而KnCMPSO 采用基于学习的粒子更新策略不仅学习父代个体,还向精英个体或全局最优个体学习,因此具有更好的收敛性能.

表8 算法在各个实例上的HV 值Table 8 The HV value of the algorithm on each example

同时,考虑到本文求解实际问题的特殊性,Kn-CMPSO 在解的初始化过程中提出了一种基于约束处理的初始化方法,为了验证该方法的优越性,本文选择采用其他3 种经典约束处理方法与本文KnCMPSO 算法框架结合构成新的算法,包括与基于罚函数[18]的约束处理方法结合KnCMPSO-PF,与基于可行性原则的约束处理方法[21]结合Kn-CMPSO-SR 和与基于随机排序的约束处理方法结合KnCMPSO-FR[22],并将这3 种算法与本文算法进行实验对比,实验结果见表9.由表9 可以看出,KnCMPSO 在所有实例上均取得了最优结果,这主要归因于KnCMPSO 将约束处理融入到粒子初始化以及更新的过程中,能有效地解决多种复杂约束,保证算法迭代过程中生成的解都为可行解,且在迭代过程中采用基于区间扰动的变异策略来提升种群的多样性,提高了算法的搜索效率.而其他算法在迭代过程中生成了部分不可行解,导致算法搜索效率下降.

表9 算法在各个实例上的HV 值Table 9 The HV value of the algorithm on each example

4 结束语

本文以异构无人机协同作战为背景,针对无人机协同多任务分配问题建立了包含多种约束条件的异构无人机协同多任务分配问题模型.为了求解此模型,本文提出了基于拐点的协同多目标粒子群优化算法KnCMPSO,并设计了4 种不同规模的实例进行仿真实验.实验结果显示本文所提的算法在多样性和收敛性上均优于其他的对比算法,表明本文所提算法能够有效求解无人机协同多任务分配问题.

KnCMPSO 算法采用混合编码方式以及基于约束处理的初始化方法,能有效避免不可行解的生成,采用协同进化策略将多目标优化问题转为各目标维度上的单目标优化问题,同时设计相应的搜索策略提升算法的收敛性和多样性,因此可以很好地适用于多目标多约束的无人机任务分配问题.但由于KnCMPSO 算法的编码和搜索策略是根据异构无人机任务分配问题的特性进行设计,对于其他的多目标多约束混合变量优化问题,还需研究特定的编码方式和搜索策略来进行求解.

本文提出的模型虽然考虑了更加符合实际情况的约束条件和目标函数,但是相比于现实作战环境的复杂性还存在一定的差距,为了更进一步提高任务分配模型的有效性,未来在构建无人机任务分配模型时将考虑更多符合实际的约束条件和目标函数.

附录A

表A1 和表A2 分别展示了实例3 的目标和无人机的各种属性.表A3 和表A4 分别展示了实例2 的目标和无人机的各种属性.表A5 和表A6 分别展示了实例1 的目标和无人机的各种属性.

表A1 实例3 中目标属性值Table A1 The target attribute value in example 3

表A1 实例3 中目标属性值 (续表)Table A1 The target attribute value in example 3(continued table)

表A2 实例3 中无人机属性值Table A2 Attribute value of drone in example 3

表A3 实例2 中目标属性值Table A3 The target attribute value in example 2

表A4 实例2 中无人机属性值Table A4 Attribute value of drone in example 2

表A5 实例1 中目标属性值Table A5 The target attribute value in example 1

表A6 实例1 中无人机属性值Table A6 Attribute value of drone in example 1