高速动车组数据驱动无模型自适应控制方法

李中奇 周 靓 杨 辉

动车组的自动驾驶系统是智能高速铁路发展的关键技术之一[1],如何在动车组运行速度越来越快、运行环境越来越复杂多变的情况下设计出效果好的控制器仍然是个难点.

针对动车组运行控制问题,国内外学者已经发表了众多的研究成果,大体上分为基于模型和数据驱动的控制方法.其中,基于模型的控制方法研究有: 文献[2]利用有效性评价指标确定最优的预测模型个数,然后采用减法聚类方法(一种用来估计一组数据中的聚类个数以及聚类中心位置的单次算法)建立多模型集合,设计了多模型广义预测控制器,但文章只是建立了列车运行过程的线性模型,对于模型参数不确定性没有很好的体现出来;文献[3]尝试采用极大似然估计法对列车模型的非线性部分进行系数辨识,取得了不错的效果,但极大似然法有可能在计算时陷入局部收敛,并且需要了解系统的部分特性.以上方法研究对象为单质点列车,与单质点模型相比多质点模型更接近列车实际运行状态.文献[4]提出了一种列车制动过程的辨识方法.首先通过分析多质点列车实际制动过程,并将该过程描述为单点时延模型,随后将基于Picard 迭代的辨识方法(常微分方程解的一种主要近似计算方法)应用于该时滞系统.文献[5]分析了列车运行的动态过程,考虑车厢类型及运行状态,建立了列车非线性多质点动力学模型,对其设计速度环自适应鲁棒非线性预测控制器.文献[6]建立高速动车组的强耦合模型,设计分布式神经网络滑模控制策略.其运用到的子空间辨识方法对模型结构先验知识需求较少,但本质上还是基于模型的控制方法.文献[7]提出了一种自适应数值方法来解决列车最优控制问题,通过对控制输入引入二元函数,对其进行松弛,并对松弛施加惩罚函数,将问题转化为参数优化问题.文献[8]分析了货运列车的控制原理,包括安全要求、快速运行、周期性制动等,提出了一种快速列车运行仿真算法.上述文献的控制策略设计与稳定性分析往往需要预先获取系统模型参数,或者需要对系统非线性部分进行线性化逼近.倘若系统模型未知或者存在较大扰动等情况,这些方法很难适用.

无模型自适应控制(Model-free adaptive control,MFAC)仅利用被控系统的输入输出数据进行控制器设计,是一种典型的数据驱动控制方法,由侯忠生在其博士论文中提出[9].MFAC 在满足一定假设条件的基础上,通过引入伪偏导数概念,在离散系统的每个工作点处,建立一个等价的动态线性化模型,然后利用这个动态线性化模型设计控制器、结构自适应律以及构建稳定性分析等.经过多年发展,已经在许多实际系统中得到了成功应用[10-16]: 例如文献[14-15]将MFAC 运用到汽车轨迹跟踪问题上;文献[13,16]将MFAC 运用到机器人等不确定系统中;还有与其他控制方法相结合的研究,文献[12]考虑将MFAC 与滑模控制相结合,设计不确定机器人系统的无模型自适应滑模控制,为MFAC与其他控制方法的结合提供参考.将MFAC 运用到轨道交通领域的研究有: 文献[17]结合动态线性化技术和预测控制,通过在线求解列车系统每个采样点的有限域闭环最优控制问题,得到当前控制量;文献[18]将列车输入输出数据转换为紧格式数据模型,在速度和牵引/制动力约束下,提出了基于执行器故障的无模型自适应容错控制方法;文献[19]将传统无模型自适应控制用于单质点列车速度跟踪控制当中.以上方法对系统进行线性化处理时,仅考虑了系统下一时刻的输出变化量与当前输入变化量之间的关系.原系统中所有可能的复杂行为,如非线性、参数时变或结构时变等,都压缩融入时变参数中.所以该方法运用到实际系统中时,需要设计更为复杂的时变参数估计算法才能获得较好的控制效果,加大了设计难度,且缺乏设计灵活性;文献[20]针对高速列车运行控制中的牵引/制动力约束和执行器故障问题,提出了基于偏格式动态线性化的无模型自适应容错控制.上述方法的研究对象均为单质点列车/地铁列车系统,与实际情况中多质点/多动力单元系统不符,且均未考虑能量损耗指标.

基于以上分析,本文提出了一种改进的适用于高速动车组的偏格式动态线性化无模型自适应控制(Partial form dynamic linearization-improved model-free adaptive control,PFDL-iMFAC)方法.

1)与文献[19]采用的紧格式线性化(Compact form dynamic linearization,CFDL)数据模型相比,本文采用的偏格式线性化方法综合考虑下一时刻输出变化量与固定长度滑动时间窗口内的输入变化量之间的关系,而非笼统地将原系统所有可能的复杂行为特征都融入到伪偏导数(Pseudo partial derivative,PPD)中.PFDL 数据模型中伪梯度的维数虽然增加了,但每个分量的动态行为变得更简单,复杂性相较于PPD 更低,参数估计算法的设计和选择也更加容易.本文丰富了动车组运行控制理论,也给其他一些运行控制方法提供节能策略(如最优控制等).

2)与文献[19-20]使用的单质点列车模型相比,本文考虑的多动力单元模型更符合列车的实际情况.此外,考虑在输入准则函数中加上对能量函数的惩罚项,为动车组的跟踪精度和能量损耗提供了一种折中的方法.

3)与文献[4-5]相比,本文的算法不依赖动车组动力学模型,是一种数据驱动控制算法.

本文结构如下: 第1 节给出了高速动车组模型结构(为列车运行仿真提供数据支持);第2 节提出了改进的动车组无模型自适应控制器,并对其稳定性和收敛性进行了严格的证明;第3 节是仿真分析;第4 节是总结和展望.

1 动车组运行过程动力学分析

动车组的牵引制动系统是由多个相对独立的动力单元组成的[21].其运行过程各动力单元除了受自身控制力(牵引/制动力)的影响外,还受相邻单元的车钩作用,其纵向动力学描述如图1 所示[22].图中中间车厢(轮子为黑色的车厢)为装备了牵引单元的动力机车,首尾两节车厢为拖车.

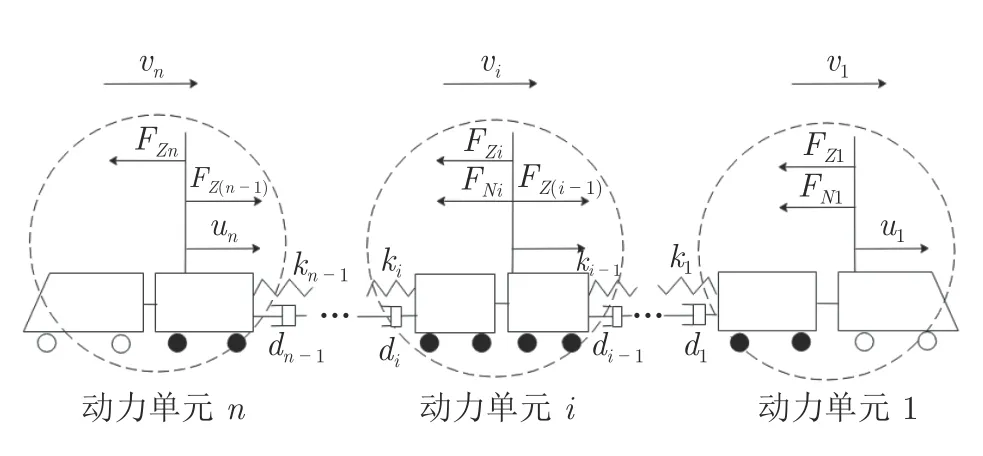
图1 动车组运行过程动力学描述Fig.1 Dynamic description of electric multiple unit operation process

以六动两拖的CRH380A 动车组为对象进行研究,该动车组有T1+M1+M2+M3+M4+M5+M6+T2三个独立的牵引动力单元[22],编组方式如图2 所示.根据牛顿运动学定律分析列车动力单元的受力情况,各动力单元上均受到了牵引力或制动力、基本阻力、车间作用力.

图2 CRH380A 型动车组动力单元分布Fig.2 Distribution of CRH380A electric multiple unit power unit

综上,根据各动力单元的动力学过程分析,将列车三动力单元模型的数学方程表示为:

ui(i=1, 2, 3) 为列车在不同工况下第i动力单元产生的牵引力或制动力;mi(t) 、vi(t) 、xi(t) 分别为第i节动力单元的质量、速度和位移;FNi(t) 为列车运行时第i动力单元所受到的基本阻力,ai、bi、ci为运行阻力系数;FZi(t) 为第i动力单元和第i+1 节动力单元间的车间作用力,k为相邻动力单元的弹性系数,d为阻尼系数.

将FZi(t) 和FNi(t) 代入式(1),得到高速动车组纵向动力学模型[23]:

各动力单元的控制力作为输入,其速度作为输出,共同构成动车组多输入多输出(Multiple-input multiple-output,MIMO)系统.动车组实际运行中,易受环境、路段变化的影响,列车模型中质量参数、阻力系数、弹簧系数及阻尼系数都存在不确定性,同时模型中还存在着非线性项[24].若采用非数据驱动控制方法设计控制器需考虑各动力单元的耦合关系,计算量巨大.为此本文设计改进的偏格式动态线性化无模型自适应控制器,对动车组进行速度跟踪控制.

2 改进的动车组无模型自适应控制器

本节结合无模型自适应控制与PFDL 数据模型,并加上对列车能量消耗的限制,设计出了一种新的列车节能控制方案,即PFDL-iMFAC.该算法不仅考虑了列车速度的跟踪误差还考虑列车能量的损耗.PFDL-iMFAC 不需要精确的列车动力学模型,是一种数据驱动的控制算法,适用于强非线性,强耦合的系统.

2.1 动态线性化

传统的CFDL 方法仅考虑了系统在下一时刻的输出变化量与当前时刻的输入变化量之间的关系[25].然而,动车组运行系统的输出不仅仅取决于某一个时刻的控制输入.基于以上考虑,在对数据线性化处理时,可将一个固定长度滑动时间内的所有输入变化量对下一时刻输出变化量的影响都考虑进来,这即是PFDL 数据处理方法.理论上,使用该方法可以很好地捕获原系统中存在的复杂动态,并且该动态线性化方法可有效地将系统复杂性分散降低[26].

动车组的输入输出数据集合可等效如下多输入多输出离散时间非线性系统:

式中,u(t)∈Rm,v(t)∈Rm分别表示系统t时刻的输入和输出;nu,nv为输入和输出阶数;g(·) 为一个非线性且时变的函数.定义为滑动时间窗口 [t-L+1,t] 内的所有控制输入组成的一个矩阵,形式如下:

满足t≤0 时,有其中L为控制输入线性化的长度整数.

对形如式(5)的系统,可以给出如下2 个假设.

假设1.非线性时变函数g(·) 对系统输入u(t)的偏导数为连续的.

由假设1 和假设2 可得到定理1.

定理1.如果非线性时变系统(5) 满足假设1和假设2,当则一定存在一个叫做伪分块雅可比矩阵的参数矩阵ΦP,L(t),使得系统可以等价为偏格式动态线性化的数据模型式(9)[27-28],L为给定维数:

任意时刻t,时变参数矩阵ΦP,L(t)=[Φ1(t),···,ΦL(t)]均为有界,相应的子方阵:

式中,i=1,···,L. 当L=1 时,PFDL 数据模型转换为CFDL 模型.

定理1 已被严格证明[27],选择不同的线性化长度常数L可以得到不同的PFDL 数据模型,合理选择时变参数矩阵和L可以提高数据模型对原系统描述时的灵活性.

2.2 控制系统设计

在文献[19]的基础上,使用PDFL 方法,再考虑能量函数的惩罚项,PFDL-iMFAC 选择新的性能指标函数:

式中,vd为参考输出; Λ＞0 为权重因子,作用是限制控制输入的变化;ζ‖u(t)‖2是为了限制列车的能量损耗.根据式(7),可以将式(9) 写成:

将式(10)对u(t) 求一阶偏微分并令其为0,可得如下控制律表达式:

由于式(11)中包含矩阵求逆,当系统维数较大时,运算量过大.为此,可参考单输出的控制算法,简化后的算法为:

式中,ρi ∈(0, 1),加入的作用是使得算法PFDLiMFAC 更具一般性.

接着,需要对时变参数矩阵ΦP,L(t) 进行实时估计,引入参数估计准则函数[27-28]:

式中,µ＞0 作用是约束相邻参数的变化率.

极小化参数估计准则函数(13),并同理式(12)的推导,可得到以下参数估计算法:

为了增强参数估计算法的鲁棒性,给出一种参数重置算法[27-28]:

式中,b1、b2为较小的正数,满足 |Φij1(t)|≤b1,b2≤|Φii1(t)|且≤ab2,1≤a;初始化值,初始化值; s ign(·) 为符号函数.

综上所述,由控制律(12)、估计算法(14)和重置算法(15)共同构成动车组的节能控制器PFDLiMFAC.将控制律(12)写成如下形式:

式中,α1、α2、α3如式(12)所示.

改进的列车无模型自适应控制结构框图见图3.

图3 改进的动车组无模型自适应控制结构框图Fig.3 An improved block diagram of model-free adaptive control structure for electric multiple unit

将所求的控制序列代入各动力单元模型(4)中,即可得到各动力单元速度.由式(16)可以看出,列车节能控制算法在控制的过程中只需各动力单元模型所产生的输出数据,因此该算法是数据驱动控制算法.此外,控制律中的增益α3会被伪偏导数的更新算法影响,换句话说,PFDL-iMFAC 的增益会根据系统时变信息实时更新.因此,与传统控制算法的固定增益相比,PFDL-iMFAC 控制方案更具有优势.

注1.选择不同的控制输入线性化长度常数L可以得到不同的PFDL 数据模型.通过合理地选择ΦP,L(t)和L可提高动态线性化数据模型对原非线性系统进行等价描述时的灵活性.

2.3 算法收敛性证明

注2.PFDL-iMFAC 的控制律具有遗忘因子α1,这使得原型PFDL-MFAC 的收敛性分析方法不再适用.此外,遗忘因子与PPD 参数和惩罚因子有关,这使得以下的收敛性分析比原型MFAC 更为复杂.

ΦP,L(t)的有界性已被证明[27-28],下面证明系统输出误差收敛.当L=1 时,PFDL-iMFAC 转换为CFDL-iMFAC.为方便描述,以下给出m=1,L=1情况的稳定性分析,其他情况证明过程类似.

根据式(12),给出m=1、L=1 时的控制律:

同理,时变参数矩阵ΦP,L(t),式中为时变参数Φ(t)的估计值.类同假设1 和假设2,给出以下假设.

假设3.对于形如式(5)的单输入单输出系统,非线性时变函数g(·) 对系统输入u(t) 的偏导数为连续的.

假设4.对于任意时刻 0≤t1/=t2和u(t1)/=u(t2)有|v(t1+1)-v(t2+1)|≤b|u(t1)-u(t2)|,即系统满足广义的Lipschitz 条件.其中b为一个大于0 的常数.

引理1.如果非线性时变系统满足假设3 和假设4,采用节能控制方法iMFAC,则有任意t=0, 1,···,T,当t趋于无穷时,输出误差收敛到一个与ζ有关的常数σ.即 l imt→∞|e(t)|≤σ;当ζ=0,limt→∞|e(t)|=0.

证明.首先定义输出误差:

由式(18)和模型 Δv(t+1)=Φ(t)Δu(t) 可得:

重写控制律(17):

进一步,式(20)可以写成以下形式:

将式(21)代入式(19),推导出:

显而易见,如果g(t+1) 是收敛的,那么|e(t+1)|同样也是收敛的.根据式(30),可推出:

引入PPD 的有界性,任意时刻t,Φ (t)≤常数b,该有界性已被证明[9].

进而,可知以下关系:

将式(36)代入式(35),推导得出:

式中,ω=d2u(0).

根据式(37)和 0＜M2＜1,不难得到:

因为 0＜d1＜1,所以如果ω=d2=0,也就是ζ=0,那么就能得出收敛性结论:

3 仿真实现及分析

以济南到徐州东区间运行的CRH380A 动车组为对象进行仿真研究.列车牵引单元的最大输出为500 kN,制动单元的最大输出为500 kN,车间最大耦合力为1 000 kN,列车牵引力/制动力变化量最大允许值为60 kN/s.列车车厢实际速度可以通过传感器获得.仿真系统具体参数如表1 所示.

表1 CRH380A 型动车组模型参数Table 1 The CRH380A electric multiple unit model parameters

注3.模型(4)只产生所需数据,本身不参与控制器设计.

分别采用CFDL-MFAC[19]、PFDL-MFAC、PFDL-iMFAC 三种方法进行仿真验证.对比分析速度跟踪效果、控制力变化、加速度变化情况以及能量损耗等指标,验证本文方法的优势.

3.1 仿真设置

采样周期设置为1 s,采样样本为4 750 个.各个控制方法对比时,使用同一模型用以产生输出数据.系统的初始条件设置为v1(1)=v2(1)=v3(1)=vd.CFDL-MFAC、PFDL-MFAC、PFDL-iMFAC 参数:Λ=0.02,ρ=ρ1=ρ2=0.9,µ=1,η=1,b1=b2=0.5. 各方案的参数矩阵初值分别为Φ1(1)=0.5ones(3, 3),ΦP,L(1)=[0.5I,0.5I,0]T,ones为全1 矩阵.PFDL-iMFAC 的能量限制常数ζ=0.0225.

3.2 本文方法与其他方法的速度跟踪及误差对比

图4 为CFDL-MFAC[19]、PFDL-MFAC、PFDL-iMFAC 三种方法的速度跟踪对比图,图5 为其速度跟踪误差对比图.

由图4(c)和图5(c)可以看出,由于只考虑当前时刻输入对输出的影响,传统CFDL-MFAC 在列车启动阶段效果较差,而且误差要比PFDL-MFAC和PFDL-iMFAC 大,跟踪误差变化不平稳,具有较大突变,只能稳定在[-0.516 km/h,0.459 km/h]之内;另外,由速度跟踪对比图4(a)和图4(b)以及各动力单元误差图5(a)、图5(b)可以看出,PFDLMFAC和PFDL-iMFAC 两种控制方法的跟踪性能所差无几,整个过程各动力单元速度误差范围分别稳定在[-0.151 km/h,0.134 km/h] 和[-0.151 km/h,0.150 km/h] 之内,这是由于PFDL-iMFAC 控制方法是一种既考虑跟踪精度,又考虑能量损耗的方法.能量损耗情况在第3.4 节处讨论.

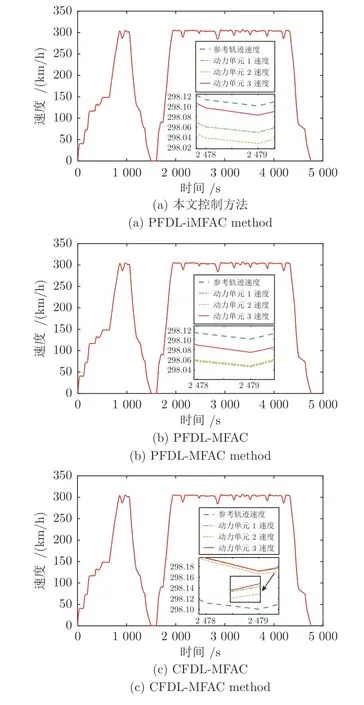
图4 本文方法与其他方法速度跟踪曲线对比Fig.4 The velocity tracking curves of the proposed method are compared with those of other methods

图5 本文方法与其他方法各动力单元速度跟踪误差对比Fig.5 The velocity tracking errors of the proposed method are compared with those of other methods

3.3 本文方法与其他方法控制力及加速度变化对比

图6 为各个控制方案的单位控制力变化图,可以看出,在启动、制动、惰性时本文提出的PFDLiMFAC 和PFDL-MFAC 方案各动力单元给出的单位控制力满足恒牵引力启动、恒功率运行等要求[29],牵引/制动力范围分别在[-43 N/kN,36 N/kN]和[-48 N/kN,42 N/kN] 内,在工况过渡阶段,控制力也能以一定的速率缓和变化.传统MFAC 在启动、制动、经过过分相时存在较大的控制力变化,牵引/制动力范围在[-50 N/kN,51 N/kN]内,给列车运行带来一定程度的安全问题.

图6 本文方法与其他方法单位控制力变化对比Fig.6 The variation of unit control force is compared with other methods

由图7 各个控制方案的加速度变化图可知,传统MFAC 方法加速度变化过快,范围在[-1.0849 m/s2,0.8987 m/s2],乘客的舒适度不满足.而采用PFDLMFAC、PFDL-iMFAC 方法的高速动车组加速度过度变化平缓,除了启动阶段,范围分别在[-0.6572 m/s2,0.6310 m/s2] 和[-0.7309 m/s2,0.7272 m/s2] 之间,满足乘客的舒适度要求.列车运行的加速度在[-1 m/s2,1 m/s2] 范围内时,乘客感觉舒适[29].

图7 本文方法与其他方法加速度变化对比Fig.7 The acceleration changes of the proposed method are compared with other methods

3.4 各个控制方法的若干性能指标对比

为了直观分析各个控制器的控制性能,考虑用均方误差(Mean square error performance,MSE)、最大加减速度(Maximum acceleration/deceleration,MAXA)和能量损耗(Wastage,W)三个性能指标,对控制器进行评价:

表2 展示了MFAC、PFDL-MFAC、PFDLiMFAC 三种控制方法的控制性能.性能指标的计算方式如式(40)～ 式(42)所示,式中i表示第i个动力单元;n为动力单元总数;t和T分别为当前采样时间和总时间.由均方误差指标可以看出,PFDLMFAC 与PFDL-iMFAC 的跟踪性能不相上下,但是PFDL-iMFAC 控制方案是最节能的.比起MFAC 控制方案,PFDL-iMFAC 可以节约9.863%的能量.从最大加/减速度可以看出,使用MFAC控制方案的列车,最大加/减速度为1.085 m/s2,变化偏大;PFDL-iMFAC和PFDL-MFAC最大加/减速度较小,分别为0.657m/s2和0.731m/s2,也意味着MFAC 不利于乘客的舒适性要求,而其他两种可以达到要求.综上,本文提出来的PFDLiMFAC 控制方案能让动车组以最低的能量消耗,较小的跟踪误差运行.

表2 各个控制方法的若干性能指标对比Table 2 Comparison of several performance indexes of each control method

4 结束语

本文针对高速动车组自动驾驶系统,提出一种改进的偏格式动态线性化无模型自适应控制方法.该方法在MFAC 的基础上,考虑滑动时间窗口,并在输入准则函数中加上对能量函数的惩罚项,得到PFDL-iMFAC 控制器.通过与传统MFAC、PFDLMFAC 对比,仿真结果表明PFDL-iMFAC 控制方案: 1)实现了比MFAC 方法对给定速度更高精度的跟踪控制,误差范围在 [-0.191 km/h,0.182 km/h]之间,满足列车速度误差要求(30 km/h 以上不超过速度值的2%,30 km/h 以下±2 km/h),达到列车的安全且准时运行;2) 控制力变化更平稳,各动力单元加速度变化范围均在[-0.6572 m/s2,0.6310 m/s2],满足乘客的舒适度要求;3)能量消耗最小,比起MFAC控制方案,PFDL-MFAC 和PFDL-iMFAC 分别可以节约5.04%和9.86%的能量;本文提出来的PFDL-iMFAC 控制方案能使动车组以最小的能量消耗,较小的速度误差跟踪目标曲线.

在本文基础上,今后将进一步做以下研究: 1)利用智能控制方法对本文控制方法设计的参数进行参数寻优[30];2)研究提升无模型自适应控制鲁棒性的方法[31].