不确定工业过程运行指标异步更新强化学习决策算法

李金娜 袁 林 丁进良

工业过程运行指标决策的内涵是以工业过程生产指标优化为目标的运行指标决策问题(如图1 所示).生产指标是指反映企业或者生产线最终产品的质量、产量、成本和能量消耗等相关的指标,运行指标是指反映控制单元的产品在运行周期内的质量、效率、能耗和物耗等相关的指标[1-2].面对激烈的国内外市场竞争,能量节约和安全生产的民生需求和政策导向,以及原材料和运行工况(生产条件)的动态波动,研究工业过程运行指标决策问题,提高产品的质量、产量和能量使用效率等生产指标,保证安全运行,这是增强企业竞争力和可持续发展的必然选择.

图1 工业过程运行指标决策问题Fig.1 Decision-making problem of operational indices in industrial processes

关于工业过程运行指标决策问题的研究一直是工业界、学术界研究的热点.工业过程运行指标决策是一个复杂的多目标优化问题,其复杂性包括:1)工业过程通常由多个控制单元构成,每个控制单元有各自的运行指标需求,目标是协同优化整个工业过程的多个生产指标;2)生产指标和运行指标之间的动态关系呈现非线性和不确定性特征.因此,传统的利用操作人员现场经验协调各运行指标的方式无法保证工业过程生产指标的优化[1-3].那么,如何简化求解此多目标优化问题,设计一种减少计算耗时并优化生产指标的方法,是本文研究的根本动机.

相比于集中式运行指标决策方法[4-5],分布式运行指标决策方法[6-11]有利于简化求解的复杂性.文献[6,8-9]针对多个生产指标优化问题,融合性能预测与反馈控制,提出了运行指标动态校正方法.在此基础上,文献[7]引入强化学习思想,基于案例推理策略,给出了数据驱动的运行指标动态修正方法.但上述方法仍需要利用操作人员的经验调整运行指标,很难保证生产指标的优化.文献[10]采用强化学习技术,基于博弈理论,给出工业过程运行指标自学习方法,保证生产指标以近似最优的方式跟踪理想值.注意到,文献[10]没有考虑生产条件波动对生产指标性能的影响.但实际工业过程原料成分、运行工况、设备状态等多种不确定因素导致生产条件动态波动.文献[11]以最大化产品产量为目标,利用历史数据,提出了一种多执行网络集成强化学习算法,自学习决策运行指标.但该研究成果忽略了实际工业过程运行指标需要满足的约束条件,并且性能指标为单次采样时刻奖赏值,无法保证累积生产指标的优化.

综合分析上述分布式运行指标决策方法,在生产条件动态波动、生产指标和运行指标存在静态约束的情况下,如何以数据驱动的方式分布式自学习决策工业过程运行指标仍是一个挑战性难题.这是本文研究的第二个动机.

自适应动态规划技术是智能最优控制领域研究的热点.该方法的本质是采用强化学习技术求解哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman,HJB) 方程,以迭代方式求解最优控制策略[12-16].文献[10,15,17-19]等针对复杂大系统,提出了一系列自适应动态规划方法用来分布式自学习最优控制策略,优化控制系统性能.但现有分布式最优控制策略自学习方法,往往忽略了系统不确定性(如环境动态波动等) 导致的状态不确定性(随机性),无法在随机变化的环境下保证系统性能的优化,甚至无法保证系统的稳定性.针对随机最优控制问题的自适应动态规划方法还鲜见报道.文献[20]针对离散随机过程,提出了一种自适应动态规划方法,自学习最优控制策略,但解决的是单变量控制问题,并且要求系统状态转移概率矩阵已知.然而,实际工业过程生产指标状态转移概率矩阵无法准确计算.此外,现有的分布式强化学习技术中策略更新为多个控制变量同步更新,多个执行网络同步训练将产生较大的时间开销和计算负载.因此,现有的自适应动态规划技术仍无法直接用于解决本文研究的两个动机问题.

文献[21-23]利用惩罚函数和Barrier 函数能解决系统状态变量和控制输入约束问题.受其启发,本文在效用函数中引入Barrier 函数和惩罚函数,用以解决生产指标和运行指标静态约束问题.利用样本均值代替计算生产指标状态转移概率矩阵,首次提出了一种策略异步更新强化学习算法,并给出了算法收敛性的理论证明.研究中面临的挑战性难题是在保证算法收敛性的前提下,如何实现策略异步更新和如何证明算法的收敛性.为此,本文引入时钟并定义其阈值,执行集中式性能评估,多策略异步更新,并且基于随机最优控制理论,采用数学归纳法证明了所提算法的收敛性.所提出的方法不要求生产指标状态转移概率矩阵已知,多策略异步更新方式提高了学习效率,同时有效地解决了生产指标和运行指标的静态约束问题,实现了不确定工业过程生产指标优化,并且保证系统安全运行.实验验证了所提方法的有效性和可行性.

本文主要的创新点如下:

1)首次提出了一种策略异步更新强化学习算法,采用集中式性能评估,多策略异步更新,可以减少计算成本和时间,提高学习效率.并且,本文给出了所提算法收敛性的理论证明.

2)本文不要求系统状态转移概率矩阵已知,在随机自适应动态规划框架下,利用样本均值代替计算生产指标状态转移概率矩阵,提出的强化学习算法利用可测量数据,在生产条件动态波动的情况下,自学习得到的运行指标能够优化生产指标.

1 工业过程运行指标决策问题描述

工业过程的运行指标和生产指标之间的动态具有强耦合性、非线性、受生产条件变化影响等特征[1-2,10-11].本文研究的目标是在充分考虑上述特征的情况下,给出一种快速地自学习决策运行指标的方法,优化生产指标,并且保证生产指标和运行指标满足静态约束条件.本文不研究过程运行优化层和回路控制层如何设计设定值和控制输入,实现运行指标跟踪理想运行指标(如图1 所示).为此,本文首先假设生产指标与运行指标之间的动态关系如下:

式中,sk=s(k)∈Rn和aik=ai(k)∈Rqi(i=1, 2,···,m) 分别表示工业过程生产指标和运行指标,dk=d(k)∈Rκ表示生产条件,f(·) 为未知非线性连续函数.运行指标决策问题可以建模为一个部分可观察马尔科夫决策过程,并用一个六元组G=＜S,A,P,r,O,γ ＞表示,其中S、A、O分别表示状态空间,动作空间和由可观察数据构成的观察空间,r表示立即奖赏,γ(0＜γ ≤1) 表示折扣因子.P(sk+1|sk,ak) 表示在当前状态sk下,采取动作行为ak产生下一刻状态sk+1的状态转移概率.在实际的工业过程中,生产指标采样周期通常为天和小时等.本文中采样时刻k=0, 1,···表示第k天或小时.具体的状态空间、观察空间和动作空间说明如下:

1)状态空间S: 对于系统(1),生产指标sk为状态变量,sk ∈S,S是连续空间.

2)观察空间O: 在实际生产中,生产条件dk可以表示单位时间吞吐量、原料质量和运行工况等.本文假设状态变量和生产条件是可测量的,那么{sk,dk}∈O.工业生产中生产条件不可能保持不变,通常具有统计特性.受生产条件波动的影响,未来的生产指标sk+1是不确定的.

3)动作空间A:m个运行指标aik(i=1, 2,···,m) 构成决策变量,因此aik ∈A.本文假设决策是确定的,即P(ak|sk)=1,决策运行指标,优化工业过程的生产指标.实际工业过程运行指标是连续的且需要满足一定的约束条件,因此A为连续动作空间.

现有的自适应动态规划方法为解决连续动作空间的最优控制问题提供了可借鉴的理论和方法.因此,本文在自适应动态规划框架下,拟提出一种策略异步更新强化学习算法,自学习运行指标.为实现本文研究目标,本文定义如下性能指标:

式中,c(·) 是效用函数,算子 E{·}表示数学期望.

注1.本文目标是优化不确定工业过程生产指标,因此效用函数要刻画生产指标.为具体明确,本文取生产指标为产品产量s1k和产品质量s2k.目标是最大化产品产量,控制产品质量在规定范围之内.因此,改写式(2)得到如下优化问题:

问题 1.

式中,s1min、s2min、s2max为正实数.

为满足生产指标和运行指标的静态约束条件,类似文献[22-23],本文引入一个Barrier 函数:

注2.效用函数c(a1k,···,amk) 中 1/s1k表示产品产量的倒数,如果想要产品产量最大化,那么需要 1/s1k最小化.不同于文献[10-11],性能指标(8)包含了通过折扣因子γ衰减作用后累积性能的期望值.折扣因子使得邻近k时刻的产品产量比未来的值更重要.并且,性能指标中还包含了运行指标和生产指标的静态约束信息.

注3.通过引入Barrier 函数和惩罚函数,本文将静态约束转化为性能指标函数.问题2 本质上是一个最优控制问题,运行指标成为动态系统(4)的控制输入,那么最大化产品产量和控制产品质量在规定范围的多目标多约束优化问题1 被转化为单目标无静态约束的最优控制问题2.

相比于集中式控制或者变量决策,分布式控制具有减轻计算负载的优势.下面将针对优化问题2给出具体的求解算法.

2 最优运行指标决策

本节针对优化问题2,基于强化学习技术和随机优化控制理论,提出了一种策略异步更新强化学习算法,并且证明了算法的收敛性.

2.1 随机最优控制方法

由于生产条件dk的随机性特征,k时刻生产指标取值具有多种可能性.因此,利用贝叶斯法则,性能指标(8)可以改写为:

上式表明最小化jk可以等价地设计最小化的决策规则.如果固定k+1 时刻的生产指标sk+1,则有:

基于随机最优控制理论和动态规划理论[10,20,24],当所有运行指标取最优策略m)时,k时刻性能的数学期望为:

由于k+1 时刻工业过程生产指标sk+1具有不确定性,则有:

利用最优性的必要条件,最优的运行指标为:

将式(15) 代入式(14),得到离散时间HJB 方程:

注4.由式(15)可知,本文采用分布式状态反馈优化控制的方式,分布式设计运行指标.与构成运行指标增广向量,采用集中式方法设计运行指标相比,减少计算负载.

注5.根据随机最优控制理论和动态规划理论,满足式(16)的运行指标式(15)能够最小化性能指标式(8).由式(15),有即运行指标满足静态约束条件.

2.2 运行指标自学习决策方法

本节将拓展现有的自适应动态规划方法,提出一种新的运行指标自学习决策算法,在优化性能式(8)的意义下,实现: 1)产品产量最大化;2)控制产品质量在规定范围之内;3)运行指标限制在规定范围之内,实现工业过程生产指标优化并且保证安全运行.

定义1[20,22,25].如果运行指标aik(i=1, 2,···,m) 满足: 1)镇定系统式(4);2)当生产指标sk满足约束条件式(5)时,jk是有界的,那么运行指标aik称为是可允许的.

为了用数值方法求解离散HJB 方程(16),本文提出了策略异步更新强化学习算法1,图2 给出了算法1 的执行机制.

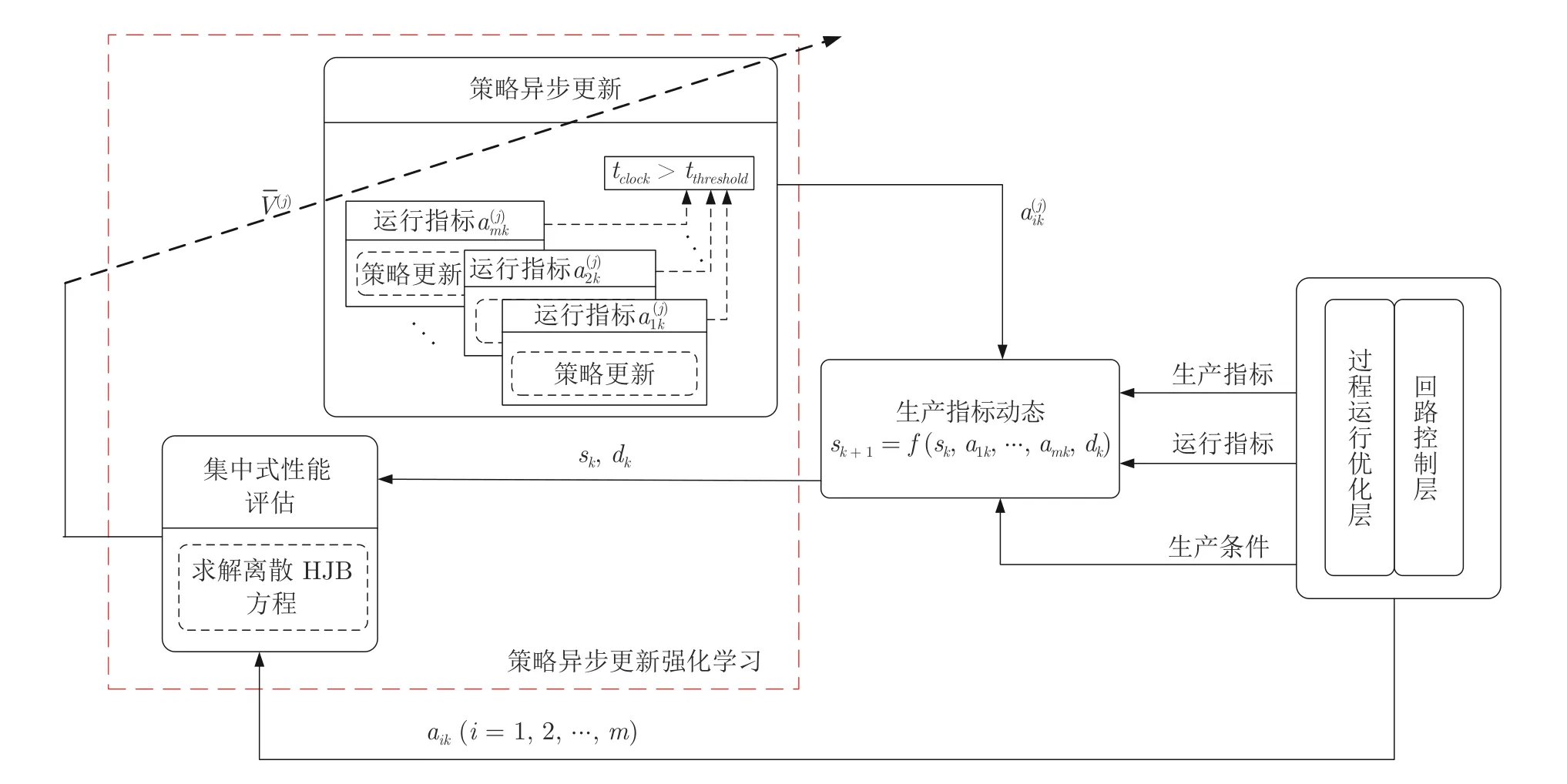
图2 运行指标自学习机制Fig.2 Self-learning mechanism of operational indices

算法1.策略异步更新强化学习算法

定理 1.假设m)可以由式(17) 和式(18) 得到,则对于所有的sk ∈S和任意迭代指标j如下结论成立

证明.1) 采用数学归纳法.当迭代指标j=1时,由式(17)定义:

注7.通过引入时钟和定义其阈值,执行策略异步更新,运行指标最终收敛到问题2 的最优解.由于算法1 本质上是强化学习方法,因此称为策略异步更新强化学习算法.

注8.不同于现有的多控制策略同步更新强化学习算法[10-11,15,17-18],本文不仅给出多个控制策略(即运行指标)异步更新算法,并且基于随机最优控制理论,采用数学归纳法给出了算法收敛性的理论证明.各运行指标分布地、异步地更新策略,而不是集中[12-14,25,28]、同步更新方式[10-11,15,17-18],其优势在于提高学习效率.

由式(17)和式(18)可知,要实现运行指标自学习决策,求解是需要解决的关键问题.但是在工业过程生产指标和运行指标动态未知、生产条件存在频繁波动的情况下,如何求解是一个难题.下面将基于提出的算法1,在多执行-评判网络结构下提出数据驱动的运行指标自学习决策算法.

2.3 多执行-评判网络结构

式中,sl(k+1)(l=1, 2,···,M) 表示在k+1 时刻随机变量s的可能取值,N为样本数,n(s=sl(k+1))表示sl(k+1)出现的次数.对于所有sk ∈Sj,利用梯度下降方法,有:

算法2.多执行-评判网络架构下的运行指标自学习决策算法

算法2 给出了具体的决策运行指标的程序.为更清楚理解算法2,图3给出了算法2 执行流程图.

图3 多执行-评判结构下运行指标自学习决策流程图Fig.3 Flowchart of self-learning decision making of operational indices with multiple actors-critic structure

注11.现有的自适应动态规划方法,通常忽视系统不确定性引发的状态不确定性.文献[20]针对离散随机过程,提出了强化学习方法,用以学习最优控制策略,但要求状态转移概率矩阵已知.本文提出的方法无需计算状态转移概率矩阵,通过计算样本均值可以计算并且提出了策略异步更新强化学习方法,用以提高学习效率.此外,本文提出的方法应用到工业过程生产指标优化问题,给出了优化生产指标并控制运行指标在规定范围之内的运行指标自学习决策方法.

注12.为计算式(43)中∂sk+1/∂ai(k),可以采用类似式(35)和式(36)的神经网络估计方法,先估计生产指标动态sk,然后再计算导数值.

注13.与经典的深度Q 网络(Deep Q network,DQN)算法以及融合DQN、执行-评判网络结构和策略梯度方法的多智能体深度确定性策略梯度(Multi-agent deep deterministic policy gradient,MADDPG)算法[32]相比,本文所提算法的不同之处在于: 1)算法2 中本文利用神经网络拟合的是值函数,而不是代替Q表的Q函数;2)算法2 中多个执行网络异步更新,而经典的DQN 算法通常是根据估计的Q函数决定一个智能体的动作,MADDPG 算法往往是多执行网络同步更新.本文多个控制策略异步更新避免了部分智能体神经网络估计控制策略用时过长,提高学习效率,并且给出了算法收敛性证明.如何将所提方法扩展到MADDPG 算法是未来拟研究的方向.

3 铁矿选矿生产指标优化试验

本节利用从中国西部某大型铁矿选矿厂获得的实际数据,包括生产指标(精矿产量和精矿品位)、7个运行指标变量和5 个生产条件变量,开展本文提出的运行指标自学习决策算法的验证,具体包括:1)实现生产指标优化,即最大化精矿产量,控制精矿品位在理想范围内,并且运行指标限制在规定范围之内;2)学习效率和生产指标对比分析.

3.1 选矿过程描述及实验设置

如图4 所示,铁矿选矿由大量工序/设备组成,包括筛分、竖炉焙烧、磨矿、低强度(弱)和高强度(强)磁选以及两个脱水单元[7,10].本文主要关注两个生产指标,即精矿产量s1和精矿品位s2.表1 分别给出7 个运行指标a1、a2、a3、a4、a5、a6、a7的含义和需要满足的约束条件.生产条件由5 个变量组成,可以增广为一个随机向量.

表1 运行指标Table 1 Operational indices

图4 选矿过程流程图Fig.4 Flow chart of mineral separation process

在本实验中,采样周期为天和小时,表示生产指标和运行指标按天或小时来测量.取精矿产量下限s1min=260 吨/小时和s1min=6 000 吨/天,精矿品位下限s2min= 53.5%,精 矿 品位上限s2max=54.5%.本文通过Matlab 软件实现算法.假设收集到的铁矿石加工历史数据有足够的代表性,可以用来反映真实生产过程.现场收集的532 个数据被分为两组,分别用于生产指标动态神经网络的训练和验证.精矿品位和精矿产量的动态模型均采用16-16-1 的神经网络结构来估计,损失函数定义为:

式中,sik为实际数据,为神经网络估计值,m为正整数.图5 给出了精矿产量和精矿品位的训练集与验证集的损失函数变化图.由图5 可以看出,模型在验证集上的误差是随着训练集的误差下降而下降的,表明本文训练得到的神经网络模型不存在过拟合或者欠拟合的现象.

图5 精矿产量和精矿品位损失函数Fig.5 Loss functions of the concentrate yield and concentrate grade

对生产条件历史数据做统计分析,生产条件向量近似服从高斯分布 N (µ,σ2),均值µ=[31.70 43.38 13.75 71.14 58.56],方差σ2=[0.92 0.44 0.57 3.62 2.75].

3.2 算法验证和结果比较

用蒙特卡洛方法产生与历史数据同分布的生产条件,评判神经网络采用2-10-1 的结构,7 个执行神经网络均采用2-14-1 的结构.神经网络的学习率为0.05,训练误差为0.001,取折扣因子γ=0.8.执行算法2,图6 和图7 分别为执行网络和评判网络神经网络权学习过程.图8 为200 天7 个运行指标实验结果,相应地图9 和图10 显示了200 天精矿品位和精矿产量的实验结果.图8 表明采用所提算法2,运行指标限制在规定范围之内.图9 和图10表明精矿品位和精矿产量满足静态约束条件.图6～图10 表明了本文算法的有效性.

图6 多执行神经网络权值Fig.6 Evolution of weights of multi-actor neural networks

图7 评判神经网络权值Fig.7 Evolution of weights of critic neural network

图8 200 天的运行指标Fig.8 200-day operational indices

图9 200 天的精矿品位Fig.9 200-day concentrate grade

为验证本文算法的优势,做了对比性实验.表2为采用本文方法、文献[11] 的多执行网络集成算法(Multi-actor networks ensemble,MAE)和文献[33]的Reinforce 算法获得的精矿产量和实际精矿产量的对比性结果.由表2 和图10可以看出,本文方法得到的精矿产量高于实际生产精矿产量.通过计算平均值,本文算法2 相比于实际精矿产量提高了约1 000 吨/天、40 吨/小时.不同于文献[11,33],本文优化目标为最大化累积产品产量,不是单次采样时刻的产量,单次采样时刻产量高不能保证累积时间内产量的最大化.由表2 可以看出,相比于文献[11]算法,本文算法提高30 天(按天采样)和1 天(按小时采样)精矿产量分别为34 167.6 吨和2 299.5 吨;相比于文献[33]算法,本文算法提高30 天和1 天精矿产量分别为36 462.2 吨和2 381.9 吨.执行类似文献[10-11]的策略同步更新强化学习算法,图11显示了10 次运行本文算法2 和策略同步更新算法的时间消耗.10 次实验中,策略异步更新强化学习算法和策略同步更新强化学习算法平均每次执行时间分别为4.83 秒与7.80 秒,表明了本文提出的策略异步更新算法提高了学习效率.实际选矿过程生产条件动态变化,针对如下三种生产条件变化均值相同µ=[31.74 43.66 13.94 71.68 58.96],不同方差:

图10 200 天的精矿产量Fig.10 200-day concentrate yield

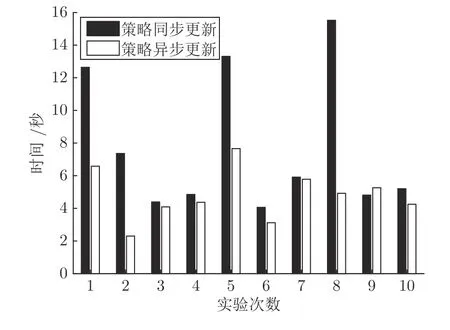
图11 策略异步更新和策略同步更新强化学习算法时间消耗对比Fig.11 Comparison of time consumption between asynchronous policy update and synchronous policy update

表2 算法的实验结果对比Table 2 Comparison results between different algorithms

工况1:=[0.68 0.64 0.48 3.93 2.59]

工况2:=[2.68 1.67 2.44 5.79 5.42]

工况3:=[2.88 3.73 4.44 8.72 8.32]

执行算法2,图12 显示了考虑工况变化和不考虑工况变化统计结果对比.结果表明: 未考虑工况变化,没有根据工况的波动调节运行指标,精矿产量变化比较平稳.而本文算法能根据生产条件变化自适应调节运行指标,优化精矿产量,平均精矿产量高于同种工况下的未考虑工况变化的值.

图12 考虑工况变化和不考虑工况变化统计结果对比Fig.12 Statistic results with and without consideration of dynamics of production condition

4 结束语

本文针对不确定工业过程运行指标决策问题,基于自适应动态规划技术,提出了一种数据驱动的策略异步更新强化学习算法,决策运行指标,并给出了算法收敛性的理论证明.该算法不要求状态转移概率矩阵已知,利用样本均值代替计算生产指标状态转移概率矩阵,采用集中式性能评估和多策略异步更新方式,利用可测量数据,自学习决策运行指标.该算法提高了分布式强化学习的学习效率,实现了生产条件动态波动环境下,工业过程生产指标优化并且保证运行指标和生产指标在规定范围之内.仿真实验验证了方法的有效性.