基于单声矢量传声器虚拟扩展的多机动声目标跟踪算法

张 君 鲍 明 赵 静 陈志菲 杨建华

声矢量传声器(Acoustic vector sensor,AVS)可同步测量空间一点处声压和笛卡尔坐标系三个正交方向上的声质点振速信息[1-4].单个AVS 利用其对频率不敏感的 “8”字形指向性,即可实现需由多个声压传声器组成阵列才可实现的声源波达方向(Direction-of-arrival,DOA) 估计.鉴于AVS 的小尺寸便携、声场信息获取等方面的优势,因此为机器人听觉感知系统的发展提供新思路.

近年来,最大似然[5]、波束形成[6]、基于子空间分解的MUSIC[7-8]、ESPRIT[9-10]等算法已广泛用于基于AVS 的DOA 估计问题.尽管小尺寸AVS 可实现DOA 估计,但其孔径一定程度上限制了角分辨率.高阶累积量处理手段的引入[11],可通过AVS虚拟扩展和量测噪声抑制达到提高DOA 估计精度的目的.实际场景中多为运动声目标,且伴随目标出生、死亡,目标数目是时变的.然而,上述算法主要针对固定数目的静止声目标DOA 估计,且未考虑相邻时间步目标状态的高度相关性.

基于随机有限集(Random finite set,RFS)理论的目标跟踪方法[12]可解决时变多目标跟踪问题.该类方法将多目标状态和量测建模为RFS,并通过多目标贝叶斯滤波传递多目标后验概率,从而达到目标数目与状态参数估计的目的.目前常用的有概率假设密度(Probability hypothesis density,PHD)[13-15]、势概率假设密度(Cardinalized PHD,CPHD)[16]、多目标多伯努利(Multi-target multi-Bernoulli,MeMBer)[17-20]以及广义标签多伯努利(Generalized label multi-Bernoulli,GLMB)[21-26]等滤波器.这些算法能够避免如多目标假设[27]、联合概率数据关联[28]等算法的数据关联,极大程度上降低计算复杂度,提高目标跟踪精度与实时性.在基于AVS 的目标跟踪实现中,文献[29-32]采用RFS来描述状态过程的随机性,并通过粒子滤波实现时变二维DOA 估计.文献[33]将MeMBer 滤波器引入单个AVS 的目标跟踪中,实现了两个不同频率窄带目标检测与跟踪.文献[34]则进一步引入交互式多模型(Interacting multiple model,IMM)和指数加权的MUSIC 伪谱似然函数以提高跟踪精度.然而,上述基于单个AVS 的目标跟踪算法最多实现双源跟踪,且无法分辨各目标的航迹信息.

基于标签RFS 理论的GLMB、δ-GLMB、Mδ-GLMB[35,36]等滤波器通过引入航迹标签信息,可解决其他非标签RFS 滤波器无法区分目标航迹的问题.Mδ-GLMB 滤波器作为一种近似的δ-GLMB方法,通过对量测-航迹的关联映射执行边缘化处理,能够减少航迹假设数目、降低计算成本.鉴于此,本文在Mδ-GLMB 滤波框架下设计AVS 虚拟扩展的多机动声目标跟踪算法,即Cum-AMMS-GLMB算法,以解决AVS 可跟踪声目标数目少、低信噪比下跟踪性能差的问题.该算法主要贡献为:

1)高阶累积量预处理的提出,能够抑制高斯量测噪声,提高目标跟踪精度.除此之外,高阶似然的设计可实现AVS 虚拟扩展.与现有基于空间谱伪似然的AVS 跟踪算法相比,可增加可跟踪目标数目.

2)实际场景中,真实声目标的运动轨迹无法由单一运动模型描述.Cum-AMMS-GLMB 算法在Mδ-GLMB 框架下嵌入IMM 思想,将表征不同运动模型的索引作为扩展状态,通过各模型间的加权更新提高跟踪性能.与现有IMM-GLMB 算法[37-39]不同,该算法量测为声目标混合信号,无需额外引入航迹-量测的关联映射,能够降低滤波主体的存储容量和计算成本,抵消预处理过程的部分计算负担.

3)实际情况下新生目标先验未知、且检测概率可时变.算法实现过程中设计了新生目标提取、以及检测概率拟合方法.其中检测概率函数通过预处理获得的归一化高阶空间谱拟合,可达到抑制杂波向可用粒子扩散、增强高似然区域粒子的目的.

除以上主要贡献外,本文还推导了多模型交互的AVS 目标跟踪的PCRLB,并通过实验验证了Cum-AMMS-GLMB 算法的可行性和有效性.

1 声目标系统建模

1.1 目标运动模型

在声目标跟踪问题中,k时刻一个单声目标状态为其中αk和βk分别表示声目标在k时刻的方位角和俯仰角分别表示速度和加速度.考虑到声目标真实运动模型未知,因此可引入多个运动模型,并通过一定的概率逼近真实声目标的运动状态.则k-1 时刻的单声目标状态向k时刻转换的运动方程为:

其中θk-1为声目标在k-1 时刻的状态.F(o)和G(o)分别对应第o个运动模型的状态转移矩阵和噪声驱动矩阵,o∈O为运动模型索引,O={1, 2, 3,···}为模型索引空间.过程噪声服从零均值,协方差为的高斯白噪声,其中σw表示加速度扰动标准差.I2表示2 × 2 维的单位矩阵

实际应用场景中,声目标可能突然出现、消失,目标状态和数目均随机变化.每个时刻的声目标状态和数目的变化可由标签RFS 描述,即:

其中M(k) 为k时刻的声目标数目.L为离散标签空间.lk,m表示k时刻第m个声目标对应的标签,每个标签存储二维变量 (t,i),其中t记录目标出生时刻,i用于区别同时出生的目标.上述标签RFS对每个声目标状态θ∈Θ 赋予独一无二的标签l ∈L,能够将目标状态扩展为{(θ,l)∈Θ×L},从而解决非标签RFS 无法区分声目标航迹的问题.

1.2 AVS 量测模型

单个AVS 可同时测量声场中声压和三个正交方向上声质点振速,并且不敏感于声目标的频域特征,直接对时域数据进行处理即可实现声目标DOA 估计.假设k时刻M(k) 个声目标以{αk,m,βk,m},m=1,···,M(k)的来向入射到AVS,该时刻传声器共接收到L个采样快拍,则 4×L维接收数据模型为:

依据式(2),AVS 在k时刻的接收数据可表述为如下非线性量测方程:

其中Hk(·) 为非线性量测函数.量测模型是不同状态声目标的混合信号,仅存在一组 4×L维的量测值,因此量测集可表示为Zk={Zk}.对于给定声目标状态θk ∈Θk,其被检测的概率为pD,k(θk),漏检概率为qD,k(θk)=1-pD,k(θk) .量测噪声Vk为高斯噪声,因此k时刻量测Zk服从复高斯分布Zk～CN(Hk(Θk),RZ,k),即似然函数可表示为:

2 AVS 虚拟扩展的多机动声目标跟踪算法

本部分提出AVS 虚拟扩展的多机动声目标跟踪算法,即Cum-AMMS-GLMB 算法.算法首先引入预处理方法,设计新的高阶似然函数模型,以抑制量测噪声、增加可跟踪目标数目.然后在Mδ-GLMB 框架中引入IMM 概念[37-40],并将运动模型索引作为隐含状态扩展到声目标状态中,进一步推导给出Cum-AMMS-GLMB 算法的预测、更新步骤.

2.1 AVS 虚拟扩展预处理

声目标DOA 估计通常由空间谱估计方法实现.文献[41]指出阵列可估计声源数目为:

其中 r ank(·) 表示矩阵求秩,RZ为接收数据的协方差矩阵,p为信号待估参量维度,q为声信号维度,N表示阵列通道数目.对四通道AVS 的二维DOA估计而言,其可估计声目标数目满足M′ ≤2.67,即最大可分辨声目标数目为 2.实际应用场景中,通常期望使用更少的传感器跟踪更多的声目标.本部分引入高阶累积量预处理方法,并设计新的似然函数模型,通过对AVS 的虚拟扩展增加可跟踪声目标数目.

2.1.1 高阶累积量预处理

在执行高阶累积量预处理前,需对式(2)所示AVS 接收数据模型做如下假设:

1) 声目标信号sk,m,m=1,···,M(k) 均为零均值、平稳、非高斯随机过程,且在统计上彼此独立;

2) 量测噪声Vk为零均值高斯噪声,该高斯噪声与入射声目标信号统计上独立.

根据以上假设,预处理方法适用于高斯噪声背景下非高斯信号处理.现实世界中,声源通常为非高斯信号[11,42-43].因此,上述假设在实际应用中同样适用.

根据高阶累积量的独特性质[43-44],对式(2)进行四阶累积量预处理:

其中 1≤i1,i2,i3,i4≤4 为AVS 通道取值.cum{·}表示四阶累积量计算. (·)*表示复数共轭.sk,m(l′)表示 1×L维向量sk,m的第l′个元素.Vk(i,l′) 表示 4×L维量测噪声Vk的第 (i,l′) 个元素.Ak(i,m)表示k时刻阵列流型Ak的第 (i,m) 个元素为k时刻第m个声目标的四阶累积量.已知量测噪声为高斯白噪声,预处理过程首先依据 “高斯随机变量的高阶累积量恒等于0”的性质可得(1/从而达到抑制量测噪声的目的.然后,依据性质 “多个随机变量的一个子集同其他部分独立,则高阶累积量为0”可得,当且仅当m=i=j=n时,等于否则为0.最终,式(5)预处理结果中抑制了高斯量测噪声,仅剩余目标信号的四阶累积量以及包含DOA信息的阵列流型的叠加信号.

将式(5)预处理结果放入 42×42维累积量矩阵:

其 中Bk=[b(αk,1,βk,1),···,b(αk,M(k),βk,M(k))],b(αk,m,βk,m)=a(αk,m,βk,m)⊗a*(αk,m,βk,m),四阶累积量矩阵与协方差矩阵RZ,k的区别在于: 1) 抑制了高斯量测噪声;2) 预处理后的四通道AVS 虚拟扩展为一个导向矢量形如b(αk,m,βk,m) 的16 通道冗余虚拟阵列.去除冗余通道后,虚拟阵列为一个10 通道传声器.根据式(4)可得,AVS 虚拟扩展后的可估计声目标数目满足M′ ≤8.33,即预处理后最大可估计8 个目标.

总结来说,高阶累积量预处理的引入不仅能够抑制高斯量测噪声,还可通过AVS 的虚拟扩展以增加可跟踪声目标数目.

2.1.2 量测似然函数

基于高阶累积量预处理的噪声抑制和阵列虚拟扩展优势,本部分建立高阶似然函数以增加AVS可跟踪声目标数目.与MUSIC 空间谱[7-8]获取手段相同,对式(6)累积量矩阵进行特征分解,获取噪声子空间Uk,v和信号子空间Uk,s.基于信号、噪声子空间的正交性,声目标DOA 可由获取.因此,定义k时刻AVS 虚拟扩展的高阶似然函数为:

其中η=diag{1, 0, 0, 1, 0, 0}用于提取声目标状态中的DOA 信息,b(ηθk)=a(ηθk)⊗a*(ηθk).高阶似然函数g(Zk|θk) 是AVS 虚拟扩展后的空间谱,表示在量测数据为Zk的条件下目标状态θk的概率,形式上可近似理解为概率密度函数.

式(7)所示高阶似然函数与粒子滤波似然函数具有类似效果,当目标状态接近真实声目标状态时,似然函数很大,否则很小.尽管似然函数中并未直接体现式(3)量测模型中的量测Zk和噪声Vk,但用于构建高阶似然的Uk,v是通过Zk的累积量矩阵获取,且其估计结果受Vk的影响.图1 为不同信噪比(Signal-to-noise ratio,SNR)情况下的高阶似然函数示例.当SNR 较高时谱峰尖锐,容易获得更准确的DOA,而SNR 较低时谱峰主瓣过宽,将导致DOA 估计值偏离真实值.

图1 不同信噪比下的归一化高阶似然函数示例Fig.1 Example of normalized higher-order spatial spectrum under different SNR

2.2 Cum-AMMS-GLMB 滤波算法

GLMB 滤波器可解决MeMBer、CPHD、PHD等滤波方法还需额外的航迹关联步骤才可解决的航迹区分问题[21-23].作为GLMB 滤波器的特殊形式,δ-GLMB 滤波器由于其能够降低GLMB 滤波器的内存需求和计算成本,对于目标跟踪更具优势.一个具有状态空间 Θ 和离散标签空间L的δ-GLMB RFS 的概率密度可表示为[22]:

其中L(Θ)={L(θ):θ ∈Θ}表示Θ的标签集.Δ(Θ)=δ|Θ|(|L(Θ)|) 表示不同的标签指示器,|·| 表示集合的势.每个I∈F(L) 表示k时刻的一组轨迹标签.Ξ为一离散空间,每个ξ∈Ξ 表示k-1 时刻航迹-量测的关联映射历史. (I,ξ) 表示一个假设,即轨迹集合I具有关联映射历史ξ.w(I,ξ)表示假设 (I,ξ) 的权重,p(ξ)(·,l) 为关联映射历史ξ中轨迹l的运动状态的概率密度.Mδ-GLMB 滤波器为一种δ-GLMB滤波器近似方法,相当于对δ-GLMB 中关联映射历史执行边缘化处理,其概率密度可表示为[36]:

δ-GLMB RFS 中权重w(I,ξ)和概率p(ξ)的存储容量分别为 |F(L)×Ξ| 和| Ξ|,而Mδ-GLMB RFS 中权重w(I)和概率p(I)的存储容量均为|F(L)|.可见Mδ-GLMB 滤波器在保留多目标后验关键统计量的同时,能够降低存储容量和计算成本.考虑到式(3)量测模型为所有声目标的混合信号,任何一个轨迹假设集合均与该量测映射.因此,目标跟踪过程中无需引入航迹-量测的关联映射历史,Mδ-GLMB滤波框架更适用于基于混合量测的声目标跟踪算法设计.

多目标跟踪问题中,通常选取理想的匀速(Constant velocity,CV)、匀加速(Constant acceleration,CA)、协同转弯(Coordinate turn,CT) 等运动模型对目标运动方式进行建模,然而单一运动模型无法准确描述真实目标运动状态.为此,本部分在Mδ-GLMB 滤波框架下引入IMM 思想,将包含轨迹标签的目标状态 (θ,l) 扩展为一额外增加运动模型索引的增广状态θ=(θ,l,o),设计并推导给出Cum-AMMS-GLMB 算法.算法通过不断更新多种运动模型下的加权混合目标状态,实现对多机动声目标运动状态的拟合.

2.2.1 Cum-AMMS-GLMB 预测器

给定当前时刻的多目标状态 Θ,及其标签空间L和运动模型索引空间O.每个声目标状态(θ,l,o)∈Θ 要么以ps(θ,l,o) 的概率存活到下一时刻,并以f(o)(θ+|θ,l)p(o+|o)δl(l+)的转移函数转移到新的状态 (θ+,l+,o+),要么以qs(θ,l,o)=1-ps(θ,l,o)的概率消失.幸存目标的状态集合可按照如下分布而得:

值得注意的是,上述状态转移过程中仅将状态θ转移到状态θ+,而标签被保留l+=l,运动模型索引{o,o+}作为隐含状态仅用于对多种运动模型下状态的加权混合求解,并不显式体现.对于标签空间为B的新生目标状态集合Θ(b),其分布如下:

仅考虑声目标的幸存、新生、死亡.下一时刻的多目标状态集 Θ+为幸存目标 Θ(s)和新生目标 Θ(b)的并集,其中标签空间为L+=L ∪B,运动模型索引空间始终为O.

假设多目标先验分布为式(9)所示的Mδ-GLMB形式,则多目标预测同样为Mδ-GLMB 形式:

不同于Mδ-GLMB 算法,Cum-AMMS-GLMB 算法预测器中的p(SI)(θ+,o+,l) 和ηS(I)(l) 则是通过多种运动模型概率和各模型下目标状态的加权混合获取.

证明.假设声目标之间独立进化,新生目标与幸存目标无关,则多目标预测为:

根据式(10)可得,下一时刻幸存多目标的状态密度

由于增广状态值为离散索引值,因此可得:

2.2.2 Cum-AMMS-GLMB 更新器

假设多目标预测为式(9)所示的Mδ-GLMB形式,则增广运动模型参数下的多目标后验具有如下Mδ-GLMB 形式:

上述更新器特点如下: 1) 算法量测模型为不同状态声目标的混合信号,无需引入航迹-量测的关联映射;2) 式(15)中的检测概率pD(θ,l) 和高阶似然函数g(Z|θ,l) 已包含目标是否被检测,无需再引入漏检概率qD(θ,l); 3) 不同于Mδ-GLMB 更新器,由多种运动模型的加权混合获取.

证明.量测Z的叠加性导致其与目标状态具有较强相关性,理论上无法分解多目标似然函数.然而高阶似然基于噪声、信号子空间的正交性构建,量测Z可等效为噪声子空间量测Uk,v.等效的量测可认为不具有 “叠加性”,因此多目标似然函数依然能够分解为g(Z|Θ)=[pD(·)g(Z|·)]Θ. 虽然g(Z|·) 中已包含杂波和目标状态的检测率,但为增强高似然区域粒子,抑制杂波粒子,更新器中依然引入检测概率pD(·). 对于g(Z|Θ)π(Θ),有:

联合上述两式,可得多目标后验为:

3 Cum-AMMS-GLMB 算法实现

式(12)～ 式(15)即为Cum-AMMS-GLMB 算法的预测器和更新器.本部分在基于AVS 的声目标DOA 跟踪场景下,设计新生目标提取和检测概率拟合方法.由于量测模型为非线性模型,最终通过序贯蒙特卡洛(Sequential monte carlo,SMC)实现算法框架下的多机动声目标跟踪.

3.1 新生目标提取

k时刻是否存在目标新生可依据k-1 时刻和k时刻量测值对应的空间谱判定.设定判断阈值thr,分别寻找k-1 时刻和k时刻的归一化高阶空间谱中峰值集合大于thr对应的目标状态集合:

新生目标的新生概率可由该状态对应的归一化空间谱幅值表示.为防止SNR 较低情况下杂波产生的虚假源对声目标跟踪的影响,引入接受系数∊B,并且令作为新生概率.∊B取一较小值即可,本文设置为∊B=0.3.

3.2 检测概率模型拟合

不同声目标状态对应的归一化高阶空间谱幅值可体现检测概率.空间谱类似于混合二维高斯分布,因此k时刻的检测概率模型可由混合二维高斯分布拟合:

其中M(p)(k) 表示当前空间谱中大于阈值thr的峰值数目为k时刻空间谱峰值中第i个峰值对应的幅值分别表示第i个峰值对应的声目标状态和协方差矩阵.图2 即为对图1(a)所示归一化空间谱通过式(17)拟合获得的检测概率函数.

图2 检测概率模型Fig.2 Detection probability model

3.3 Cum-AMMS-GLMB 算法的SMC 实现

3.3.1 初始化输入

3.3.2 预处理

对量测数据进行高阶累积量预处理,抑制量测高斯噪声和虚拟扩展AVS.具体步骤如下:

步骤 1.通过式(5)、(6)对Zk进行高阶累积量预处理获取累积量矩阵并对特征分解获取噪声子空间Uk,v.

步骤 2.通过式(7) 求解归一化高阶空间谱寻找中大于阈值thr的 峰值用于式(17)所示检测概率函数pD,k(θ) 的拟合.

3.3.3 预测器

3.3.4 更新器

最终可得k时刻多目标后验概率密度参数集为其中Hk为更新器假设数目.注意: 更新器中后验假设的标签集合依据预测假设的标签集合给定.

3.3.5 剪枝、合并及状态估计

算法的剪枝、合并以及声目标状态估计与常规δ-GLMB 算法[21-23]一致.具体处理过程如下:

步骤 10.剪枝与合并: 修剪粒子权重低于指定剪枝阈值的分量,并将粒子总数控制在最大限度内.

步骤 11.目标数目、状态估计: 确定势分布中概率最高的势(对应于目标数目),然后在该势下寻找权值比设定阈值高的分量进行目标状态提取.

依据以上Cum-AMMS-GLMB 算法步骤即可实现基于AVS 的多机动声目标跟踪.由于本文重点在于高阶似然函数的设计和添加表征不同运动模型索引的增广参数的Mδ-GLMB 算法推导,因此预测、更新器中假设截断方法参考文献[21]实现,本部分不多加赘述.

3.4 算法计算复杂度

根据上述实现步骤,Cum-AMMS-GLMB 算法的计算复杂度主要增加在以下部分:

1)四通道AVS 的高阶累积量预处理,计算复杂度为 O (N4),其中N=4 为AVS 通道数目.

2)预测部分增加了对运动模型概率的预测、更新.给定预测器中H个假设下的标签集合粒子数目J以及运动模型数目O,则运动模型概率预测、更新的总计算复杂度为其中 |L(h)| 表示第h个假设下的目标数目.

3)更新部分增加了高阶似然的求解.高阶似然通过N2×N2维累积量矩阵的特征分解获取,计算复杂度为 O ((N2)3).

因此,Cum-AMMS-GLMB 算法的主要计算复杂度为.

Cum-AMMS-GLMB 算法滤波主体部分无需引入IMM-GLMB 算法中的航迹-量测关联映射,但由于执行高阶累积量预处理,算法计算复杂度依然高于IMM-GLMB 算法.然而,后续仿真验证了该算法可增加AVS 的可跟踪声目标数目、提高跟踪性能.算法的跟踪优势可一定程度上补偿略高的计算复杂度.为降低计算复杂度,可在预处理后去除虚拟AVS 的冗余通道,从而降低矩阵特征分解的计算复杂度.除此之外,还可借鉴GLMB 快速算法[45-46],通过联合预测和更新步骤以降低计算复杂度.

4 声目标跟踪性能评价

本部分引入后验克拉美罗下界PCRLB[47]和最优子模型分配距离(Optimal sub-pattern assignment,OSPA)[48]两种指标,从不同角度评估算法性能.

4.1 后验克拉美罗界

PCRLB 能够提供随机变量估计所能达到的最低误差界,可通过比较不同条件下算法(Root mean square error,RMSE)与PCRLB 的逼近程度以评估算法跟踪性能.由于本文引入了IMM 思想,已有PCRLB 通解方法已不再适用,因此本部分推导求解多运动模型交互的AVS 目标跟踪的PCRLB.

4.1.1 基于多运动模型交互的PCRLB 推导

其信息矩阵为:

根据PCRLB 与信息矩阵的关系,最终可得k时刻目标状态分量估计的PCRLB 为

4.1.2 AVS 的目标跟踪PCRLB

根据式(18)可得声目标状态分量的转移概率为:

为便于分析,将 4×L维量测Zk记为 4L×1 维列向量则后验概率密度函数为:

其中βk为的第二项,表示k时刻声目标的俯仰角.L表示每一时刻的采样快拍数,S NR 为信噪比.

依据上述推导,以下给出基于AVS 的目标跟踪PCRLB 的求解步骤:

1) 初始化信息矩阵J0,可依据先验信息设置,无先验信息时可设为 0;

3) 根据式(25)求解θk的信息矩阵Jk,最终获得k时刻的PCRLB 为

4.2 OSPA 距离指标

OSPA 距离能够直观反映算法对于每一时刻的目标个数和状态估计误差.记 Θ={θ1,···,θm}和分别表示真实和估计的多目标状态集,则OSPA 距离定义如下:

其中 Πn表示从集合{1, 2,···}中取出m个元素进行排列的集合.c＞0 表示最小截止距离,表示θ和之间的距离在c处截断.p为阶数,用于惩罚多目标状态的估计偏差.在后续仿真实验中取c=5,p=1,其中OPSA 距离计算过程中通过匈牙利算法[49]实现最优分配问题的求解.

5 实验验证

5.1 多声源跟踪仿真

单个AVS 作为接收传感器,并放置5 个运动声目标于整个实验场景中.设置SNR 为10 dB,加速度扰动噪声标准差σw为 0.5°/s2,采样率为10 kHz,共采集50 s 数据.表1、表2 分别给出了各时间段所对应的运动模型和声目标的运动状态.

表1 各时间段对应的运动模型Table 1 Movement model corresponding to each time period

表2 声目标的运动状态和幸存时间Table 2 Motion state and survival time of acoustic targets

使用Cum-AMMS-GLMB 算法进行声目标跟踪,可得图3 所示的声目标跟踪、目标数目估计和OSPA 距离结果.跟踪结果指出Cum-AMMSGLMB 算法在声目标数目大于AVS 通道数目的情况下依然能够准确跟踪声目标.这主要是由于该算法设计的高阶似然函数可对AVS 进行虚拟扩展,从而提高AVS 的可跟踪声目标数目.

图3 Cum-AMMS-GLMB 算法的多声目标跟踪结果Fig.3 Multiple acoustic target tracking results of Cum-AMMS-GLMB algorithm

5.2 算法对比仿真

本部分对表3 所示4 种算法的跟踪性能进行比较.算法均执行IMM 处理,不同之处在于算法滤波器和似然函数的使用.值得注意的是,Cum-AMMSGLMB 算法基于Mδ-GLMB 滤波框架实现,且其量测Zk为所有声目标的叠加信号,因此无需引入Cov-GLMB 算法中的航迹-量测的关联映射历史.CBMeMBer 算法和Cum-CBMeMBer 算法并未设计对声目标状态进行航迹区分的数据关联方法,但不影响目标跟踪的实现.

5.2.1 场景一

仿真场景如下: AVS 共采集50 s 数据,采样率为10 kHz,信噪比为10 dB,σw设置为 0.5°/s2.两个声目标初始DOA 均为{180°, 30°},目标1 在第1 s 入场,初始速度为{1°/s, 0.05°/s},目标2 在第20 s 入场,初始速度为{-1°/s, 1°/s},其中不同时刻目标对应的运动模型参考表1.使用表3 所示4种算法进行仿真,可得图4(a)～ 4(b)的声目标跟踪结果.为避免实验结果的特殊性,还执行50 次蒙特卡洛实验获得图4(c) OSPA 距离以评估算法性能.

表3 各对比算法的似然函数、滤波器的区别Table 3 The difference between the likelihood function and the filter of each comparison algorithm

与对比算法相比,Cum-AMMS-GLMB 算法能够更准确的跟踪声目标轨迹和估计目标数目,并且具有更小的OSPA 距离.CBMeMBer、以及Cum-CBMeMBer 算法还需额外的数据关联才可区分声目标轨迹,而基于GLMB 框架的Cum-AMMSGLMB 算法和Cov-GLMB 算法由于航迹标签参数的引入,能够直接分辨目标轨迹.通过图4 可得,第20 s 目标新生时,引入高阶似然的Cum-AMMSGLMB 算法和Cum-CBMeMBer 算法能够准确估计目标数目,区分两个声源,而Cov-GLMB 算法和CBMeMBer 算法并未准确估计目标数目.这主要是由于AVS 本身孔径较小,且新生、幸存目标之间的角度间隔较小,因此使用传统方法对角度间隔较近目标进行角度分辨时无法准确区分目标,从而导致算法性能下降.

图4 双声目标情况下不同算法的估计结果Fig.4 The estimation results of different algorithms in the case of two acoustic targets

5.2.2 场景二

仿真场景如下: 两个声目标的初始DOA 分别为{180°, 30°}和{100°, 30°},初始速度分别为{1°/s,0.05°/s}和{-1°/s, 1°/s}.目标在不同时刻对应的运动模型参考表1.

首先评估不同信噪比下表3 所示各算法的跟踪性能.σw设为 0.5°/s2,SNR 分别从0dB 以5dB 的间隔逐渐增加到20 dB,进行蒙特卡洛实验获取图5所示RMSE 估计结果.根据图5 可得,较低SNR情况下Cum-AMMS-GLMB 算法的RMSE 低于对比算法,且随着SNR 的增加,RMSE 逐渐逼近PCRLB.除此之外,由于使用了式(7)所示的高阶似然,Cum-CBMeMBer 算法的跟踪性能同样优于相同滤波器框架的CBMeMBer 算法.

图5 不同信噪比下PCRLB 和各算法的RMSE 估计结果Fig.5 PCRLB and RMSE estimation results of each algorithm under different SNR

对于不同过程噪声下各算法性能,SNR 设置为5 dB,加速度扰动噪声标准差σw分别从 0°/s2以0.5°/s2的间隔逐渐增加到 4.5°/s2进行蒙特卡洛实验.根据图6 所示RMSE 估计结果可得,随着σw的增大,各算法的RMSE 和PCRLB 均呈上升趋势.Cum-AMMS-GLMB 算法的RMSE 性能指标优于对比算法,更逼近于PCRLB.

图6 不同 σ w 下PCRLB 和各算法的RMSE 估计结果Fig.6 PCRLB and RMSE estimation results of each algorithm under different σw

5.3 真实实验

为验证理论算法可行性,使用实验室自制AVS于半消声室进行声目标跟踪实验.实验场景如图7(a)所示,AVS 与三个声目标约在同一水平面,以保证各声目标的俯仰角近似为 0°.三个声目标分别以图7(b)的轨迹运动,静止声目标1 的方位角约为 8.1°,运动声目标2、3 中,目标2 的方位角从 6 0.95°逐渐增加到 1 13.96°,目标3 的方位角从 2 40.95°逐渐增加到299.05°.运动过程中目标1、2 一直存在,目标3 分别于一直存在、突然出现和突然消失三种情况下进行实验.实验室自制采集系统进行信号采集,采样率为3 kHz,使用Cum-AMMS-GLMB 算法进行声目标跟踪,每一秒进行一次跟踪,可得图8～10 所示的声目标跟踪结果.

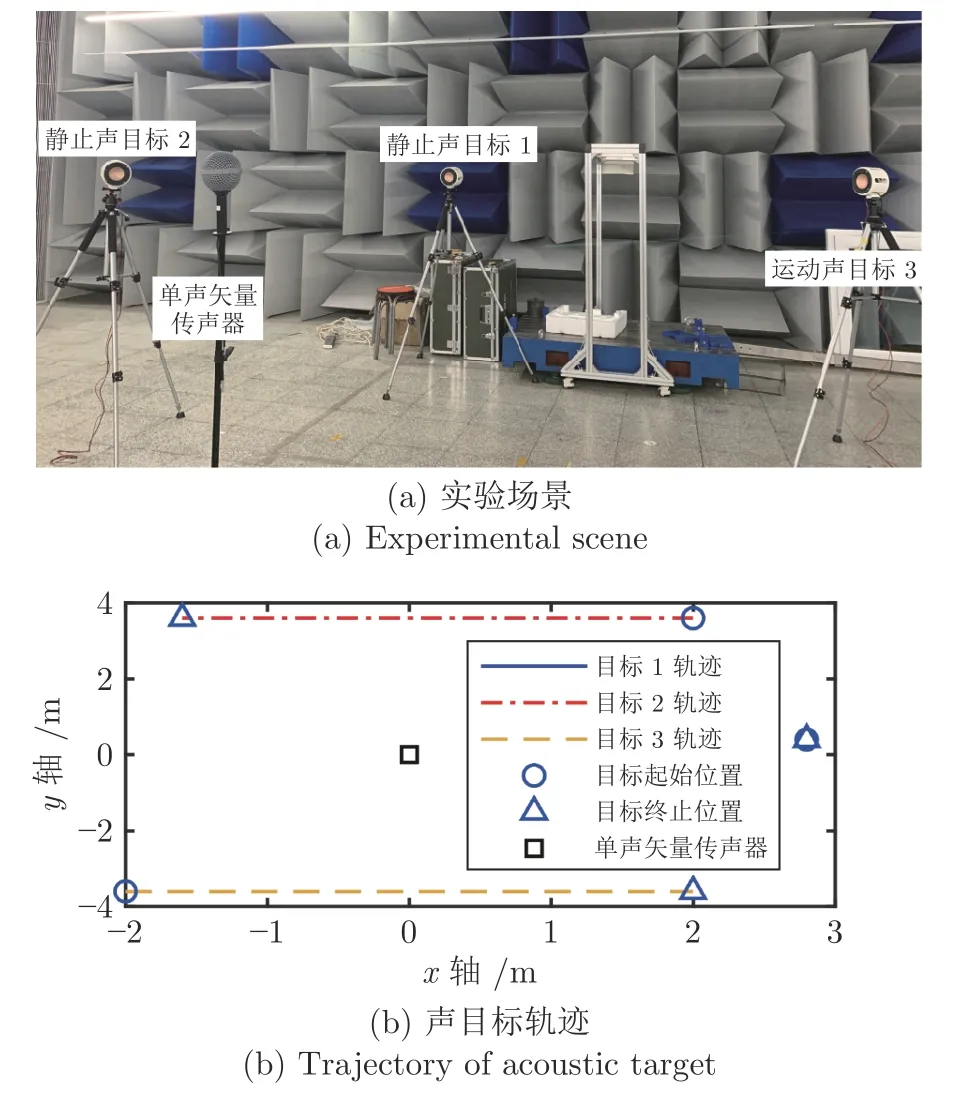
图7 半消声室声目标跟踪实验Fig.7 Acoustic targets tracking experiment in semi-anechoic chamber

根据图8 所示声目标一直存在情况下的跟踪结果可得,静止目标1 在{7.13°, 0.82°}附近波动;运动目标2 的方位角跟踪轨迹从 6 1.88°逐渐增加到 109.91°,俯仰角约在 1.02°附近波动;目标3 的方位角跟踪轨 迹 从 2 33.38°逐渐增加到3 00.95°,俯仰角约在0.66°附近波动.图9、图10 所示的声目标跟踪结果可得,在声目标突然出现情况下,目标3 在第19 s突然出现,其方位角跟踪轨迹从 2 39.01°逐渐增加到294.06°.对于声目标突然消失的情况,目标3 的方位角跟踪轨迹从 2 27.52°逐渐增加到 2 67.21°,随后在第38 s 消失.

图8 目标3 一直存在情况下的跟踪结果Fig.8 Tracing result when the target 3 is always present

图9 目标3 突然出现情况下的跟踪结果Fig.9 Tracing result when target 3 suddenly appears

图10 目标3 突然消失情况下的跟踪结果Fig.10 Tracing result when target 3 suddenly disappears

以上三种不同场景的跟踪结果中,声目标2、3的跟踪结果存在波动.这主要是由于真实DOA 轨迹为测量声目标在起始、终止位置处的连线,而在匀速移动声目标2、3 的过程中会产生抖动,从而导致运动目标的估计轨迹存在角度波动.不考虑这一不可避免的因素和传声器自身的测量误差,图8～10所示的声目标跟踪结果可得,Cum-AMMS-GLMB算法估计的目标跟踪轨迹与真实运动轨迹基本一致,该算法是可行、有效的.

6 结论

本文提出的基于AVS 的Cum-AMMS-GLMB算法,解决了AVS 可跟踪目标数目少、跟踪性能较差的问题.算法中高阶累积量预处理的引入和高阶似然函数的建立,不仅有效抑制了高斯量测噪声,还通过AVS 的虚拟扩展,提高了可跟踪声目标数目.Cum-AMMS-GLMB 算法更适配于声目标运动模型多样的实际场景.在Mδ-GLMB 滤波框架下,算法通过多种运动模型的加权混合以逼近目标的真实运动状态,获得了优于单一运动模型的跟踪效果.该算法无需引入航迹-量测的关联映射,能够降低滤波器的存储容量和计算成本,从而抵消了预处理过程的部分计算负担.除此之外,算法通过归一化高阶空间谱实现对检测概率函数的拟合,增强了高似然区域粒子,抑制了杂波向可用粒子的扩散.实验验证了算法的可行性和有效性,并且较已有基于AVS 的声目标跟踪算法的性能更优.显然所提小尺寸、便携AVS 的多目标DOA 跟踪,对未来机器人听觉跟踪系统的设计具有重要参考价值.