一种用于目标跟踪边界框回归的光滑IoU 损失

李 功 赵 巍 刘 鹏 唐降龙

目标跟踪是计算机视觉领域里的基础任务之一.随着深度学习在各个领域里日益成熟的广泛应用,基于深度网络的目标跟踪方法[1]取得了显著的提升和进步.与目标检测方法[2]类似,边界框预测模块在目标跟踪方法里也是至关重要的一环,它的性能直接影响目标跟踪模型准确性.交并比(Intersection over union,IoU)是衡量跟踪准确性的重要评估指标,定义为用来衡量预测的边界框与真值框B的相近程度.对于两个不同的跟踪器,即便跟踪器的分类模块都能够定位到目标所在位置,但边界框预测模块的性能不同仍可能导致预测结果的IoU 相差甚远,所以训练边界框回归准确甚为重要.从时间发展的顺序上看,边界框回归方法可分为2 类: 第1 类是基于ℓn-norm 损失的回归,可表示为其中常用的两种损失ℓ1-norm 和ℓ2-norm 都有缺陷,前者难以收敛到更高的精度,而后者在训练初始时不稳定.虽然Girshick[3]提出的ℓ1-smooth 损失,可以较好地解决上述两个问题,但是基于ℓn-norm 的回归损失更备受诟病的是边界框各个参数在优化过程中相互独立,缺乏对IoU 的考虑.第2类损失函数是基于IoU 损失的回归.IoU 损失[4]衍生自IoU 指标,避免预测框的参数在回归过程中互不关联.然而IoU损失LIoU有两个固有缺陷: 一个是当预测框与真值框不相交时LIoU为常量 1,其梯度无法下降,从而边界框回归分支的参数得不到更新;另一个是在IoU 取得最优值时LIoU的梯度不存在,边界框难以收敛到IoU 最优处.其实LIoU的固有缺陷继承自IoU 指标.虽然随后的GIoU (Generalized IoU) 损失[5]、DIoU (Distance-IoU)损失[6]、CIoU (Complete-IoU)损失[6]和EIoU (Efficient-IoU)损失[7]等对预测框的中心或尺寸提出了不同的惩罚项来增加LIoU在边界框不交叠时的梯度,但是附加的惩罚项并不能改善LIoU在最优值处的梯度不存在的问题.

上述基于IoU 的损失方法[4-7]已经暗示在回归过程中不应该忽视边界框参数之间的关系.但是都没有明确究竟是何种关系.边界框通常由4 个参数确定,但在不同的研究中参数的含义有所不同,可以由边界框的中心和尺寸表示为B(x,y,w,h)[3,8-10],或者是由左上角点和右下角点表示为B(xmin,ymin,xmax,ymax)[11-12],又或是由给定的一点到四边的距离表示为B(xt,xb,xl,xr)[4,13-14].其实上述表示都是等价的,可以相互转化.为方便下文描述,本文统一以B(x,y;w,h) 形式表示边界框.不妨将预测框B～(x,y;w,h)的4 个参数划分为2 组,一组是中心位置 (x,y),另一组是尺寸 (w,h).显然,对中心位置来说,追求预测框中心与真值框中心重合总是最优的,即便有时预测框中心在某个邻域内波动不会使IoU 下降.一个显而易见的事实是,不存在中心偏离可以使IoU 上升的情况.但对尺寸来说并非如此,当预测框中心发生偏离时,追求预测框的尺寸与真值框的尺寸相同却不是最优的.

本文明确给出在回归过程中边界框若取得IoU 最优其参数之间应服从的定量关系.概括地说,中心 (x,y) 在回归过程不需要顾及此时尺寸(w,h)处于何种情况,而尺寸 (w,h) 在回归过程中需要考虑到中心 (x,y) 所在何处,最优尺寸(w*,h*)=arg minw,hIoU(B～;B)=f(x,y) 与 中 心 (x,y) 存在 明确的函数关系.本文从一个新的角度看待边界框回归问题,将边界框与二元统计分布作一一映射,从优化两个统计分布之间散度的角度研究边界框回归.散度量化了两个不同分布之间的差异,这种散度自然蕴含预测框各参数之间的关系,可以避免人为设计额外的惩罚项对预测框尺寸或形状做出限制.本文从优化两个分布之间散度的角度提出了一种光滑IoU (Smooth-IoU,SIoU)损失,该损失函数在全局上光滑,对于不同的研究对象,光滑的含义也有所区别.在本文中称在开集X∈Rn上的函数f:X →R 是光滑的,如果f是C1类的,C1类的函数必然是可微的.在本文的定义下,光滑性也可以称作连续可微性,且极值唯一.光滑性确保了在全局上梯度存在使得边界框更容易回归到极值处,而极值唯一确保了在全局上可梯度下降更新参数,从而克服了IoU 损失的固有缺陷.提出的光滑IoU 损失自然蕴含边界框各参数之间特定的最优关系,其唯一取极值的边界框可使IoU 达到最优.而且提出的光滑IoU 损失具有比IoU 损失更快的回归性能.另外,提出的光滑IoU 损失可以很容易集成到具有边界框回归分支的视觉跟踪方法中.为了评估提出的光滑IoU 损失,本文将其集成到跟踪深度网络模型SiamFC++等中,并在主要的基准LaSOT、GOT10-k、TrackingNet、OTB2015 和VOT2018中进行了评估.本文主要贡献为:

1)明确给出在回归过程中最优边界框各参数之间满足的定量关系.

2)从优化散度的角度提出光滑IoU 损失,该损失函数自然蕴含边界框各参数之间特定的最优关系,在全局上连续可微,且唯一极值可使IoU 最优.提出的损失函数避免了IoU 损失的固有缺陷.

3)提出的光滑IoU 损失可以容易集成到先进跟踪网络方法,在主流的测试基准LaSOT、GOT-10k 和TrackingNet 等上取得显著的提升.

1 相关工作

1.1 边界框回归损失

自Fast-RCNN[3]提出以来,ℓ1-smooth 损失[3]就被广泛地应用在目标检测或跟踪任务中训练目标边界框的回归[8-10,12].ℓ1-smooth 损失结合了ℓ1-norm 和ℓ2-norm 中互补的良好性质.然而,对于相同的ℓ1或ℓ2误差(只要不为0),可以回归出多种大小及形状不同的边界框,而这些预测的边界框所对应的与真值框的IoU 却不尽相同,方差较大,有较强的随机性,不能准确地反映IoU 指标.Rezatofighi 等[5]展示了一些ℓ1-norm 和ℓ2-norm 相同但IoU 指标不同的示例.为此,Yu 等[4]将IoU 指标演化为IoU 损失LIoU,通过直接优化IoU 的方式边界框各参数可以作为一个整体进行回归.Rezatofighi 等[5]提出了一种广义的IoU 指标 GIoU 及其演化的损失函数LGIoU,以代替IoU 用于评估和训练边界框回归,GIoU 损失纠正了IoU 损失在预测框与真值框不相交时梯度无法下降的弊端.Zheng 等[6]提出了DIoU 损失函数LDIoU,在IoU 损失的基础上附加了一种关于预测框中心与真值框中心的归一化距离的惩罚项RD,相较于IoU 损失和GIoU 损失加快了收敛速度.同时,Zheng 等[6]在DIoU 的基础上发展出了CIoU 损失函数LCIoU,该损失函数综合考虑了3 种几何属性,分别是IoU、中心点距离和宽高比率,使得收敛速度进一步加快.与CIoU 类似,Zhang 等[7]提出了另一种高效的IoU 损失函数EIoU 损失LEIoU,该损失函数同样有3 种几何因素的度量,分别是IoU、中心点的距离以及边长差异.基于IoU 损失可被统一地表示为其中B)为各自不同的惩罚项.本文提出的光滑IoU 损失直接从散度方面构造全局光滑且极值唯一的损失函数,没有以LIoU作为基本损失,从而避免了LIoU带来的缺陷.

上述相关的边界框回归损失方法均假定边界框参数为确定变量而直接回归边界框,除了这种处理方式外,另一种处理方式是将描述边界框的关键点视为随机变量.关键点可以是角点或中心点等,通过预测关键点的热力图推断关键点最可能的位置.热力图可视为关键点服从某种统计分布的假设,对热力图的分布则通常采用Focal loss[15]训练.Gidaris 等[13]在提出的LocNet 中,预测边界框的4个边框所在位置的置信度,从而置信度最高的位置被推定为存在边框.Law 等[12]在提出的 Corner-Net 中设计了一种角点池化操作生成边界框的左上角和右下角点的热力图,并提出改进的Focal loss用于训练,而对于角点精度的偏置则采用ℓ1-smooth损失进行回归.然而,如果仅仅依靠预测左上角和右下角来确定边界框,则容易导致错误匹配而误检.Zhou 等[14]在提出的CenterNet 中定义了一种适配的Focal loss 用于训练边界框中心的热力图以减少错误匹配,而对于中心点精度的偏置以及边界框尺寸则采用ℓ1-norm 损失进行回归.另外,文献[11]提出的方法则假设预测框的角点位置服从参数待学习的正态分布,并假设真值框的角点位置服从狄拉克δ分布.通过以狄拉克δ分布为目标优化正态分布实现边界框回归.然而,在上述文献[11-14]里用来描述边界框的关键点是独立优化的,没有考虑关键点与IoU 的关系,其缺点与ℓn-norm 在某种程度上类似,都依赖于各关键点是否被预测得非常准确;而且对热力图的训练增加了网络参数的数量和网络结构的复杂性.

本文提出的光滑IoU 损失将表示边界框的 4个参数视为一个整体进行回归,在回归过程中能够照顾到IoU 信息而产生IoU 友好的结果,而且本文提出的光滑IoU 损失本质上是在最小化两个统计分布之间的散度,在不增加网络复杂度的同时隐含地表达了将边界框关键点视为服从某种分布的随机变量这一处理方式.

1.2 深度跟踪器的边界框预测

GOTURN[16]是第一个基于边界框回归的深度网络跟踪方法,直接回归当前帧的目标框相对前一帧目标框的偏移.随后的SiamRPN[8]和增强版的DaSiamRPN[10]结合了SiamFC[17]的孪生网络和Fast R-CNN[3]的区域候选网络(Region proposal network,RPN),估计边界框相对各个阳性锚框的偏移量,并从中选出分类置信度最高的作为预测框.然而Jiang 等[18]论证了分类置信度最高的边界框并不一定是与真值框吻合最优的.因此,SPM-Tracker[19]扩展了SiamRPN 方法,提出了精细匹配阶段,旨在从粗略匹配阶段选出分数最高的k个候选框提炼最终预测框.而SiamRPN++[9]则在分类置信度分支和边界框回归分支里提出了逐通道的互相关层,并通过多层级联的方式提高了分类置信度和回归精度的正相关性.上述基于锚框的深度网络方法通常采用ℓ1-smooth 损失训练边界框回归分支.

尽管基于锚框的跟踪方法仍有进一步优化网络和提升性能的空间,但基于无锚框的跟踪方法则受到越来越多的青睐.现有的研究工作和实验已经表明一些基于无锚框的深度网络方法比基于锚框的网络方法更准确,同时网络参数的精简使得跟踪器在训练和跟踪时更高效.SiamFC++[20]建议目标跟踪模型的训练不应该介入尺度或长宽比率等先验分布的信息例如锚框,其原因是定位和尺度等粗糙的锚框带来的误差可能拖累跟踪器的性能.SiamFC++摒弃了预设的锚框,并将预测的目标从阳性锚框的偏移量转化为更精细的每个阳性位置到 4 条边线的距离.随后的基于无锚框的方法如 SiamBAN[21]、SiamCAR[22]、Ocean[23]和无锚框全卷积孪生跟踪器(Anchor-free fully convolutional siamese tracke,AFST)[24]等也采用类似的预测每个正样本位置到四边距离作为网络输出的方法.值得一提的是,SiamBAN[21]、SiamCAR[22]、Ocean[23]和AFST[24]均采用IoU 损失训练边界框的回归.

本文将提出的光滑IoU 损失,应用到具有代表性的无锚框深度跟踪器 SiamFC++[20]、SiamBAN[21]和SiamCAR[22],通过替换其原有的IoU 损失,作为对比以评估光滑IoU 损失的性能.

2 光滑IoU 损失

2.1 从散度视角优化边界框IoU 的动机

为方便描述,先定义一些必要的表示记号.Bg(xg,yg;wg,hg) 代表真值框,Bp(xp,yp;wp,hp) 代表预测框,(xΔ,yΔ):=(xp-xg,yp-yg) 代表预测框的中心位置相对于真值框中心的偏差.

图1 给出了深度目标跟踪模型的基本框架,本文不妨忽略与研究内容无关的分类或中心度分支ψcls的网络结果,仅关注由孪生骨干网络φ提取的特征图经过边界框回归分支ψreg输出每一帧预测的目标边界框.在训练深度目标跟踪模型的边界框回归分支时,如果中心偏差 (xΔ,yΔ) 难以消除,预测框的尺寸 (wp,hp) 若以ℓ2-norm 损失仍然向着真值框的尺寸 (wg,hg) 回归则不是IoU 最优的,而以IoU 损失回归则在其最优的预测框尺寸 (wp*,h*p) 上又是不可微的.所以一个自然的问题是如何即时调整预测框尺寸 (wp,hp) 的回归目标,使损失函数面向更高的 IoU 指标光滑地回归.

图1 深度目标跟踪模型的边界框回归示意图Fig.1 The schematic of bounding box regression in deep tracking model

为了解决上述问题,本文从最小化统计分布之间散度的角度看待边界框回归问题.首先本文将边界框与二元正态分布建立一一对应关系,如图 2 所示.具体地,将预测框Bp(xp,yp;wp,hp) 的中心位置(xp,yp) 和尺寸 (wp,hp) 分别视为二元正态分布N(µp,Σp) 的均值µp=(xp,yp)T和边缘分布的标准差,即Σp=这样预测框Bp(xp,yp;wp,hp)与二元正态分布 N (µp, Σp) 建立了一一映射.类似地,真值框Bg(xg,yg;wg,hg)映射为均值为µg=(xg,yg)T,协方差矩阵为的二元正态分布N(µg,Σg).

图2 边界框类比为正态分布的示意图Fig.2 The schematic of bounding box analogized as Gaussian distribution

需要阐明的是,与现有的相关工作[11-14]的区别在于,本文并不是假定边界框的4 个参数本身为服从二元正态分布的随机变量,而是将其一一映射为确定二元正态分布具体形式的参量,可以理解为边界框蕴含了一种图像区域每个像素属于目标物体的置信分布,该置信分布应该反映出越靠近边界框中心位置的像素属于目标物体的置信度越高的特点,从而隐含地表达了一种以边界框中心位置为关键点的热力图.

由此,将边界框的回归问题转化为最小化二元正态分布之间差异问题.以常见的KL (Kullback-Leibler)散度DKL(N(µg, Σg)||N(µp, Σp)) 量化二元正态分布 N (µp, Σp) 和 N (µg, Σg) 之间差异为例进行分析,基于KL 散度的边界框回归损失函数为:

显然,不同于IoU 损失,式(1)在边界框全局上是可微的,而且式(1)表达了KL 散度与IoU 指标呈某种非线性负相关关系.当KL 散度越小,说明2 个二元正态分布 N (µp, Σp) 和 N (µg, Σg) 越接近,则与之对应的预测框Bp与真值框Bg就越接近,IoU(Bp;Bg)总体表现为上升趋势.当且仅当预测的边界框与真值框完全重合时,KL 散度减小到最小值 0,此时IoU 提高到最大值 1.此外,式(1)里预测框各参数不是独立的回归.预测框的最优尺寸与其中心偏差 (xΔ,yΔ) 有关.当且仅当中心偏差 (xΔ,yΔ)=(0, 0) 时,其最优预测框尺寸为真值框尺寸 (wg,hg); 否则,相较于ℓn-norm 损失,式(1)不再以 (wg,hg) 作为预测框尺寸的回归目标,而是能够调整预测框的最优尺寸以获得更高的IoU.但是式(1)还没有使预测框尺寸达到IoU 最优.在第2.2 节里,将给出在式(1)的启发下发现的一种可与IoU 协调的光滑损失函数.

2.2 光滑IoU 损失及预测框中心与尺寸最优关系

沿用Bp(wp,hp;xp,yp) 和Bg(wg,hg;xg,yg) 分别表示预测框和真值框,以及 (xΔ,yΔ) 表示预测框的中心偏差.在前文中指出中心偏差 (xΔ,yΔ) 的回归是独立的,不需要考虑预测框尺寸 (wp,hp) 的情况,而预测框尺寸 (wp,hp) 在回归过程中需要考虑到中心偏差 (xΔ,yΔ) 的情况,因此本节主要探讨在预测框尺寸 (wp,hp) 上的最优关系以及光滑的损失函数.首先构造如下损失函数:

本文定义一种描述预测框中心偏差程度的变量.

定义1.令 (xΔ,yΔ) 表示预测框中心偏差和(wg,hg)表示真值框尺寸.称dH(xΔ,yΔ;wg,hg):=为预测框中心相对真值框中心的调和归一化偏差.

接下来,阐述IoU 最优的预测框尺寸与调和归一化偏差dH有关.首先讨论式(2)构造的光滑损失LSIoU在功能上等效于IoU 损失LIoU的情况.

图3 给出了一个LIoU:=1-IoU 和式(2) 中LSIoU在满足dH ＜2 条件下在相同点取最优的可视化示例,示例中真值框尺寸为(wg,hg)=(10, 10)以及中心偏差为 (xΔ,yΔ)=(2, 2.5),水平坐标面表示预测框尺寸.由图3 可以看出,两者均在预测框尺寸为处取得最小值.命题1 指出如果中心偏差满足dH ＜2,则覆盖真值框的最小边界框即是IoU 最优的.当中心偏差为 (0, 0) 时,最小覆盖真值框的边界框尺寸与真值框相同,此时LSIoU的优化目标退化为真值框本身,与其他边界框回归损失如ℓn-norm 或LIoU的目标相容.

图3 LIoU 和 LSIoU 在对数坐标下的可视化图像示例Fig.3 A visualized example of LSIoU and LIoU viewed in the logarithmic scale of horizontal axis

由命题1 可以推出,调和归一化偏差dH满足其他情况时IoU 最优的预测框尺寸.

仿照命题1 的证明,可以证明命题2 和命题3,本文不再赘述.上述3 个命题揭示了在回归过程中IoU 最优的边界框各参数之间蕴含的定量关系.命题2 指出了LIoU最优的预测框尺寸不唯一的情况.在边界框中心处于特殊位置(即dH=2) 时,LIoU增加了边界框形状或尺寸在回归过程中的不确定性.LSIoU则不存在这个问题,最优化LSIoU所取得的真值框的最小覆盖框是唯一的.

虽然命题3 指出了在预测框中心偏差满足dH ＞2时,仍以真值框的最小覆盖框作为动态回归目标不是IoU 最优的,但是注意到最优化LSIoU仍然可以取得一个良好的预测框.图4 显示了一个中心偏差落入dH ＞2 的示例,实线框代表以gc为中心的真值框,而其余虚线框代表以pc为中心的预测框.在中心距离d相同的情况下,图4(a)所显示的为依据IoU 指标最优的预测框,但是其GIoU 指标相对较低.图4(b)所显示的为LSIoU最优的边界框,虽然其IoU 指标略微低于IoU 最优的边界框,但是其GIoU 指标则显著高于图4(a).另外,值得注意的是,如果引入额外的先验知识(例如CIoU[6])将预测框限定为保持与真值框相同的宽高比,其不同尺度的边界框如图4(c)所示,可以看到其所能达到的IoU 上界低于LSIoU最优的边界框所取得的IoU指标.因此,即便遵循LSIoU最优所得到的最小覆盖真值的边界框在IoU 意义下不是最优的,但是综合IoU 和GIoU 指标来看,依然不失为一个很好的策略.

图4 当 d H >2 时最优化 LSIoU 和 LIoU 的边界框示例Fig.4 Illustration of predicted box that minimizes LSIoU and LIoU if dH >2

概括地说,式(2)给出的损失函数LSIoU具有以下特性:

1)尺度不变性.与LIoU一样,LSIoU仍然是回归尺度不变的损失函数.尺度不变是指在损失相同的情况下预测框与真值框之间的IoU 不会随着边界框尺度的变化而变化.相对于尺度变化的损失函数例如ℓn-norm 损失,尺度不变的损失函数可以减轻目标尺寸的多样性带来的不利影响.

2)正定性.当且仅当预测框与真值框完全重合时,即IoU 指标达到最大值 1 时,LSIoU=0 达到最小值.由此,LSIoU可以视为一种散度函数反映出预测框与真值框的相近程度,或者更准确地说,LSIoU反映出以预测框代替真值框而产生的损失程度.

3)光滑性与极值唯一性.当预测框与真值框不相交时,有LIoU=1,此时∇LIoU=0,无法通过梯度下降更新预测框参数;并且LIoU取最优时∇LIoU不存在,导致回归的结果不稳定.而LSIoU在全局上偏导数存在且连续,预测框参数可以通过梯度下降更新,且更容易回归到极值处,当且仅当LSIoU取最优时,有∇LSIoU=0,LSIoU达到极值.

2.3 预测框中心偏差的正则项

为了使预测框的中心位置在回归过程中尽可能满足条件dH ＜2,提出一种针对LSIoU的正则项:式中,α=2 arctan(wg/hg) 是由真值框尺寸所确定的参量,而β是需要满足β＞1 的参量.图5 给出了一个由正方形真值框确定的正则项RS的图像示例,阴影区域满足dH ＜2,箭头代表某一梯度轨迹.由于一般的ℓ2正则项其等值线是同心圆,梯度总是指向 (0, 0),这样中心偏差(xΔ,yΔ)位于平面内任何方向上的机会都是均等的,并不适用于SIoU 损失的特点.由图 5 可以看出,不同于一般的ℓ2正则项,本文针对SIoU 损失设计的正则项 [xΔ,yΔ]Sα,β[xΔ,yΔ]T,其关联的非对角正定的二次型矩阵Sα,β使 [xΔ,yΔ]Sα,β[xΔ,yΔ]T的等值线为椭圆形并且长轴恰位于直线dH=0.所以正则项 [xΔ,yΔ]Sα,β[xΔ,yΔ]T在等值线上的梯度指向是不同的,具有方向偏好.如果以梯度下降法更新 (xΔ,yΔ),则 (xΔ,yΔ) 的轨迹可以向着dH ＜2区域靠拢如图 5 所示,增大落入到区域dH ＜2 的机会,同时也可以增加LSIoU的凸性.注意到正则项[xΔ,yΔ]Sα,β[xΔ,yΔ]T是一个仅和中心偏差(xΔ,yΔ)有关的函数,而与预测框尺寸 (wp,hp) 无关,所以正则项的加入并不会使LSIoU违反最佳尺寸与中心偏差的关系.

图5 正则项 R S 的图像示例Fig.5 Illustration of regularization RS

加入中心偏差的正则项后,提出的光滑IoU 损失函数LSIoU可如下表示为:

式中,γ为正则项的系数.

2.4 预测框中心偏差的光滑代理

注意到LSIoU里含有关于中心偏差的ℓ1函数|xΔ|和 |yΔ|,其在 0 处也是不可微的.针对这个问题,本文不妨构造一个近似函数以替换|xΔ| 和 |yΔ|.考虑到对于任意xΔ∈R,当λ→∞有下式成立:

式中,代表一致收敛.易知Aλ(xΔ) 是光滑的,图6给出了取不同λ值的光滑代理函数Aλ(xΔ) 的图像.这样Aλ(xΔ) 可以用来作为|xΔ| 的光滑代理.|xΔ|和 |yΔ| 在回归过程中可以分别用Aλ(xΔ) 和Aλ(yΔ)代替以保证LSIoU对边界框中心位置参数是光滑的.

图6 不同参数 λ 下 | x| 的光滑代理函数Aλ(x)Fig.6 Plot of smooth surrogate function A λ(x) for |x|with different λ controlling its shape

2.5 光滑IoU 损失的算法

在应用光滑IoU 损失训练边界框回归时需要注意其中两点: 1)容易验证当 (wp,hp) 趋 于(0, 0)时,LSIoU损失则趋于无穷,这样在训练初期可能因为预测的尺寸过小而出现梯度爆炸的情况.为了避免训练过程中的梯度爆炸,对LSIoU作了梯度截断处理,通过取:

与LSIoU最小的操作:

使预测框尺寸在wp ≤wg/2,hp ≤hg/2 时梯度不变,限制到可控范围内,同时不影响LSIoU的可微性.图7 给出了以图3 中的示例通过梯度截断后的LSIoU损失图像.2) 为了避免光滑代理函数Aλ中的指数函数可能引发机器浮点数溢出,不妨设置一个区间半径rλ ＞0,当-rλ ≤x≤rλ,取Aλ(x),否则取|x|.选取适当的区间半径rλ可以在机器所能表示的精度范围内保持连续性.应用光滑IoU 损失训练边界框回归如算法1 所示.光滑IoU 损失可以很容易代替IoU 损失函数应用在深度目标跟踪网络中训练边界框的回归.在下一节里将组织相关实验以验证提出的光滑IoU 损失的有效性.

图7 梯度截断后的 LSIoU 可视化示例Fig.7 A visualized example of LSIoU with truncated gradient

算法 1.应用光滑IoU 损失的边界框回归

3 实验和评估

本节将提出的光滑IoU 损失合并到具有代表性的基于锚点无关的目标跟踪模型SiamFC++[20]、SiamBAN[21]和SiamCAR[22]中来评估其有效性.其原本的IoU 损失LIoU训练的结果作为基线,用LSIoU替换原本的LIoU训练作为对比.实验中选择GoogleNet[25]作为SiamFC++[20]的孪生骨干网络结果.而SiamBAN[21]和 SiamCAR[22]则采用ResNet-50[26]的后三个残差块级联的方式提取特征,并遵循SiamFC++、SiamBAN 和SiamCAR 的训练过程,采用论文里报告的默认参数和每个基准上的迭代次数.实验中λ设为 2,rλ设为20.正则项系数设置为采用ILSVRC-VID/DET[27]、COCO[28]、YoutubeBB[29]、LaSOT[30],TrackingNet[31]和GOT-10k[32]作为基础训练集.然后在主流的目标跟踪测评基准平台LaSOT[30]、TrackingNet[31]、GOT-10k[32]、OTB2015[33]和VOT2018[34]上,对提出的边界框回归损失模型进行评估对比.另外,仅从跟踪结果上很难讨论边界框回归的过程是如何进行.因此本节设置了一组采样分析实验,采样的数据综合考虑了距离、尺度以及宽高比等边界框之间的关系,涵盖多种回归情况,研究光滑IoU 损失相比当前基于IoU 的损失的优越性.实验环境配备了128 GB 内存,Intel Xeon E5-2650 2.3 GHz CPU处理器,Nvidia GTX 1080Ti GPU 显卡,采用深度学习框架PyTorch 实现.

3.1 采样实验

图8 从两种分布中采样近距离和远距离的初始预测框位置Fig.8 Sample the initial predicted boxes subject to normal distribution with short and long mean-variance

图9 各种边界框回归损失比较Fig.9 Comparison among the convergence performance of different bounding box regression losses

图10 不同迭代次数的 LGIoU、LCIoU 和 LSIoU 的回归示例Fig.10 Illustration of predicted boxes via LGIoU,LCIoU and LSIoU regressing in different iterations

3.2 对比实验

本节通过5 个主流的基准测试来评估提出的光滑IoU 损失函数,用于目标边界框回归的性能.

3.2.1 LaSOT

LaSOT[30]是一个高质量的大规模单目标跟踪基准,数据集包含1 400 个视频,涵盖了视觉跟踪里14 种典型的挑战,例如遮挡、运动模糊、尺度变化等,划分为70 个常见类别,每个类别提供20 个视频,平均视频长度超过2 500 帧,总共超过352 万个人工标注的帧.LaSOT 基准的协议将其中1 120个视频作为训练集,280 个视频作为测试集,每个类别包含相同数量的视频.大规模的训练集使得跟踪器不容易出现过拟合,从而达到了测试跟踪器真实性能的目的.遵照LaSOT 基准的协议,跟踪器需在LaSOT 训练集上训练,并在LaSOT 测试子集上评估,常用的评估指标为一次性通过(One-pass evaluation,OPE)的标准化精确率图、精确率图和成功率图,其中精确率图刻画了预测边界框与标定边界框的中心位置的像素距离在阈值范围内的图像帧数所占的比率关系,精确率以中心位置误差小于20 像素的比率对跟踪器进行排名;成功率图刻画了预测的边界框与标定的边界框的重叠率(即IoU)超过阈值的图像帧数所占的比率关系,然后依据曲线下方区域面积对跟踪器进行排名.而标准化精确率引自TrackingNet[31],是为了消除精确率对图像√分辨率和边界框尺寸过于敏感,可表示为Pnorm=表1 给出了SiamFC++模型以LSIoU作为边界框回归损失训练在LaSOT上得到的测试结果.可以看出,LSIoU相对于原有的LIoU提高了SiamFC++模型性能的成功率、精确率、标准化精确率,分别相对提高 3.60%、5.05 % 和3.24 %.从LaSOT 数据集中选择了5 个代表不同类型的视频,从中抽取部分帧来显示跟踪的效果,如图 11 所示.图中虚线框标出了以LSIoU训练的测试结果,点线框标出了原始的以LIoU训练的测试结果,实线框为真值框.可以看出,LSIoU比LIoU得到的预测框更靠近真值框.为了验证本文光滑IoU 损失在其他深度目标跟踪器上也具有良好的鲁棒性和适用性,表 2 和表 3 分别报告了对SiamBAN[21]和SiamCAR[22]模型采用LSIoU替换原有的IoU 损失训练的实验对比结果.鉴于不同模型其网络结构的不同,虽然未能超过SiamFC++的表现,但LSIoU相对于原有的LIoU提高了SiamBAN 和SiamCAR 模型的性能,其中提升最显著的成功率分别相对提高5.64%和5.04%.

图11 在LaSOT 测试集上,分别以 LIoU (点线框标出)和LSIoU(虚线框标出)训练的模型 SiamFC++的可视化结果示例 (实线框为真值标签)Fig.11 Visualized tracking results of SiamFC++trained using LIoU (marked in dotted box) and LSIoU (marked in dashed box) on LaSOT(solid box denotes groundtruth)

表1 在基准 LaSOT 上,分别以 LIoU (原本的)和 LSIoU训练的模型 SiamFC++的测试结果(%)Table 1 Comparison between the performance of SiamFC++trained using LIoU (original),LSIoU on the test set of LaSOT (%)

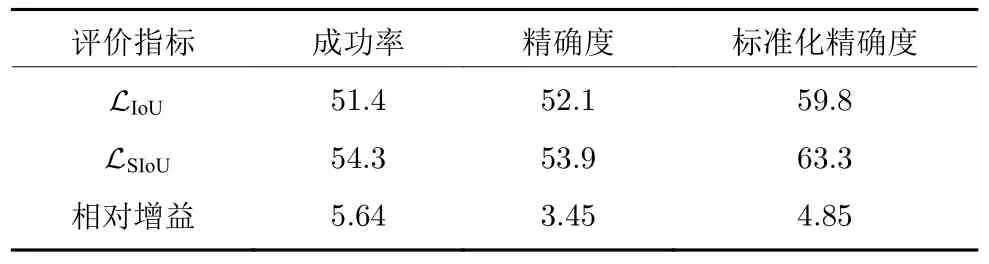
表2 在基准LaSOT 上,分别以 LIoU (原本的)和LSIoU训练的模型SiamBAN 的测试对比(%)Table 2 Comparison between the performance of SiamBAN trained using LIoU (original),LSIoU on the test set of LaSOT (%)

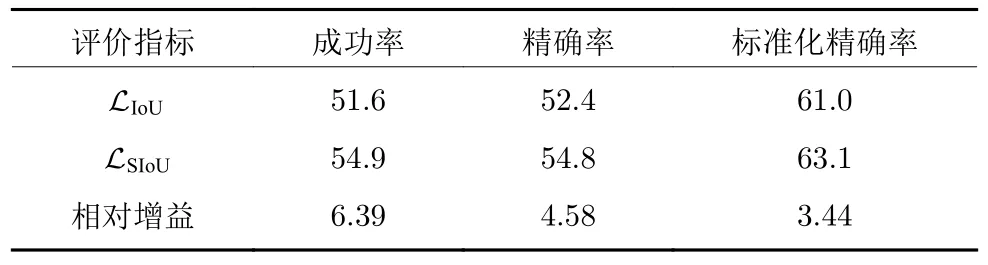
表3 在基准LaSOT 上,分别以 LIoU (原本的)和 LSIoU训练模型SiamCAR 的测试对比(%)Table 3 Comparison between the performance of SiamCAR trained using LIoU (original),LSIoU on the test set of LaSOT (%)

为了表现采用本文SIoU 损失训练SiamFC++、SiamBAN 和SiamCAR 后横向比较的性能,选取了其他9 种先进的跟踪方法进行对比,分别为SiamBAN[21]、SiamCAR[22]、SiamRPN++[9]、Siam-Mask[35]、GlobalTrack[36]、C-RPN[37]、Ocean[23]、ATOM[38]和DiMP[39].其中,Ocean[23]模型选择具有更好性能的在线更新的Ocean-online 版本.用SiamFC++(SIoU)代表以LSIoU训练边界框回归分支的版本以示区分.在LaSOT 上的成功率和精确率的对比如图12 和表4 所示,可以看出,SIoU损失方法使SiamFC++模型超越了先进的Ocean和DiMP,实现了最好的性能.与Ocean-online 相比,SiamFC++(SIoU)在3 个指标上的得分分别相对提高了1.5%、1.6%和1.8%.与DiMP 相比,SiamFC++(SIoU)在成功率上同样表现出1.5%的优势,而在精度上表现出1.9%的优势,验证了LSIoU可以更好地在复杂场景中回归不同对象边界框的能力.

表4 在基准LaSOT 上,与先进方法的性能评估对比Table 4 Performance evaluation for state-of-the-art algorithms on LaSOT

图12 在LaSOT 上评估成功率、精确率和标准化精确率结果Fig.12 Success plot with area under the curve,precision plot and normalized precision plot on LaSOT

3.2.2 GOT-10k

GOT-10k[32]一个由中国科学院发布的基于WordNet 的大型目标跟踪数据集,总共超过10 000 段视频,细分了563 类户外常见的移动物体,范围涵盖了动物、交通工具、人物、被动运动目标以及特定部位目标5 大类别,标注的边界框数量超过150 万.除了类别广泛,规模宏大,该数据集还具有训练数据统一和单样本学习等特点.依照GOT-10k 的协议,所有模型都用相同的训练数据,来保障所有模型之间的公平对比.并且为了使训练出的模型能有更强的泛化能力,基准测试集与训练集之间不存在交集.测试集包含180 段视频,分属于84 个目标类别,该测试基准评价的指标有平均重叠率(Average overlap,AO)和成功率(Success rate,SR),数值越大说明方法性能越高.表5 展示了采用LSIoU训练的SiamFC++模型在服务器上评估的结果,虽然在 S R0.75指标上性能略低于原始结果2.29%,但在 S R0.50指标上增益高达7.48% 以及在 A O 指标上增益 3.69%,同样实现了一定程度的性能改进.表 6 给出了经过LSIoU训练的SiamCAR 模型在服务器上的评估结果,3 个指标上均有不同程度的提升,除了在 S R0.50指标上性能提升最高达6.29%,在 A O 和S R0.75指标上相对基线结果分别提升了3.69%和5.22%.表 7 总结了与7 种当前先进方法MDNet[40]、SPM[19]、ATOM[38]、SiamCAR[22]、Siam-RPN++[9]、Ocean-online[23]、D3S[41]和DiMP-50[39]的对比,SiamFC++(SIoU)和SiamCAR (SIoU)代表以LSIoU训练边界框回归分支的版本.可以看出,采用LSIoU训练的SiamFC++在标准化精确度和成功率方面都表现出了优势.LSIoU使 SiamFC++的成功率超过了最先进的 DiMP-50[39]和Oceanonline[23]达1.8%,标准化精确度超过了2.2%.

表5 在GOT-10k 上,分别以 (原本的)和 训练的模型SiamFC++测试对比(%)LIoU LSIoUTable 5 Comparison between the performance of SiamFC++trained using (original),on the test set of GOT-10k (%)LIoU LSIoU

表6 在GOT-10k 上,分别以 (原本的)和 训练的模型SiamCAR 测试结果(%) LIoU LSIoUTable 6 Comparison between the performance of SiamCAR trained using (original),on the test set of GOT-10k (%) LIoU LSIoU

表7 在基准GOT-10k 上,与先进方法的性能评估对比 (%)Table 7 Performance evaluation for state-of-the-art algorithms on GOT-10k (%)

3.2.3 TrackingNet

为了进一步评估本文方法,在更具挑战性的数据集TrackingNet[31]上进行了实验.TrackingNet包含了30 132 个视频,平均每个视频471.4 帧,以及覆盖了27 个类别用于单目标跟踪器的训练,是目前目标跟踪任务里的体量最大的数据集.与GOT-10k 类似,TrackingNet 的测试集独立于训练集,并在官方评估服务器上测试,该基准测试提供了511 个视频,视频平均帧数与类别属性分布与训练集相似.与基准LaSOT 相同,评估服务器基于跟踪结果计算成功率、精确度和标准化精确度三个评估指标.表8 给出了SiamFC++模型以LSIoU作为边界框回归损失训练在TrackingNet 上得到的测试结果.可以看出,LSIoU相对于原有的LIoU提高了SiamFC++模型的性能,成功率、精确度以及标准化精确度分别相对提高1.06%、2.27 %和2.37 %.而表9 给出了与7 种当前先进的跟踪器,即MDNet[40]、ATOM[38]、DaSiamRPN[10]、Siam-RPN++[9]、UpdateNet[42]、SPM[19]、DiMP[39]在 TrackingNet 上的结果对比,SiamFC++(SIoU) 代表以LSIoU训练边界框回归分支的版本.可以看出,采用LSIoU训练的SiamFC++在精确度和成功率方面均表现最佳.如表9 所示,LSIoU使SiamFC++的成功率超过了最先进的 DiMP[39]模型1.8%,标准化精确率超过了2.2%.在如此大规模的数据集上的实验结果表明了以SIoU 损失训练边界框回归具有良好的泛化能力.

表8 在TrackingNet 上,分别以 (原本的)和训练的模型SiamFC++的测试结果(%) LIoU LSIoUTable 8 Comparison between the performance of SiamFC++trained using (original),on the test of TrackingNet (%) LIoU LSIoU

表9 在基准TrackingNet 上,与先进方法的性能评估对比 (%)Table 9 Performance evaluation for state-of-the-art algorithms on TrackingNet (%)

3.2.4 OTB2015

除了上述大规模数据的基准测试,本文也在小规模的数据集OTB2015[33]上进行了实验.OTB-2015 包含了100 个视频,涵盖了视觉跟踪里11 种典型的挑战.与LaSOT 类似,该基准测试常用的评估指标为一次性通过的精确率和成功率.表10 和表11 分别给出了以LSIoU作为边界框回归损失训练的SiamFC++模型和SiamBAN 模型在OTB2015上得到的测试结果.可以看出,虽然LSIoU相对于原有的LIoU提高了SiamFC++模型和SiamBAN 模型的性能,但提升幅度有限,成功率相对提高了分别为0.74%和0.43%,而精确率相对提高了分别为0.34%和0.55%.可能的原因是小规模的测试集对网络参数以及超参数更敏感,具有偶然性和特殊性,大规模的测试样本更能得到一般性的结果.

表10 在OTB2015 上,分别以 LIoU (原本的)和LSIoU训练的模型SiamFC++的测试结果 (%)Table 10 Comparison between the performance of SiamFC++trained using LIoU (original),LSIoU on the test of OTB2015 (%)

表11 在OTB2015 上,分别以 (原本的)和训练的模型SiamBAN 测试结果 (%) LIoU LSIoUTable 11 Comparison between the performance of SiamBAN trained using (original),LIoU LSIoU on on the test of OTB2015 (%)

3.2.5 VOT2018

数据集VOT2018[34]共包含60 个视频,虽然视频数量较少并与VOT2018 之前版本发布的数据集相同,但是对所有视频重新标定了由分割掩码外接得到的更加精确的边界框,也就是说这种边界框不再是坐标轴对齐的,给跟踪器带来了新的挑战.VOT2018 里重要的3 个评价指标: 准确率(Accuracy,A)、鲁棒性(Robustness,R) 和平均重叠率期望(Expected average overlap,EAO).准确率用来评价跟踪器的准确度,通过n次重复测试得到跟踪器在单个视频帧序列下IoU 的平均值,即A=该指标数值越大,准确度越高.鲁棒性用来评价跟踪器的稳定性,通过n次重复测试得到跟踪器在单个视频帧序列上跟踪失败的次数F的平均值,即重叠率为 0 即为跟踪失败,该指标数值越小,稳定性越高.VOT-2018 相较于其他测试基准具有的一个特色机制是会在跟踪器跟踪失败时重启,即失败发生时的5帧后重新初始化,所以平均重叠率期望是取跟踪器在非重新初始化的Nl个长度为l的视频帧序列上平均重叠率的期望值,即IoUl(i)]是VOT2018 评估跟踪算法精度的重要指标,数值越大,精度越高.表12 给出了SiamFC++模型以LSIoU作为边界框回归损失训练在VOT2018上的测试结果.由表12 可以看出,在准确率和EAO 指标上有所下降.造成这种现象可能的原因是,VOT2018 里的IoU 计算涉及到预测框与旋转的标注框之间的交叠,而非传统意义下两个坐标轴对齐的矩形框之间的 IoU,而此时并不能证明提出的光滑IoU 损失所遵从的策略仍然可以最优.所以为了应对这种评估指标,还有待对边界框回归函数做进一步研究和拓展.

表12 在VOT2018 上,分别以 (原本的)和训练的模型SiamFC++测试结果(%) LIoU LSIoUTable 12 Comparison between the performance of SiamFC++trained using (original),LIoU LSIoU on on the test of VOT2018 (%)

3.3 消融实验

为了证明提出的光滑IoU 损失与其他以IoU为基准的损失如 GIoU[5]和 DIoU[6]相比具有优势,本文在基准 LaSOT 和 GOT-10k 上对 SiamFC++、SiamBAN 和SiamCAR 模型采取不同边界框回归损失函数(即本文提出的LSIoU、LGIoU[5]、LDIoU[6]以及原本的LIoU损失)作为对比实验.表13 和表14记录了基于3 种模型的不同边界框回归损失在测试集上超过不同IoU 阈值的图像帧数所占比率.最小阈值取值为0.5,并以步幅0.05 逐次累加的方式设置更高的阈值,可以看出提出的光滑IoU 损失可以改善边界框回归的效果,虽然在高IoU 阈值下以SIoU 训练的模型测试结果所占比率不一定高于其他IoU 为基准的损失,但是这一部分的比率普遍很小,SIoU 损失在中高IoU 阈值下与其他基于IoU的损失相比优势明显,对整体指标提升的贡献更大.

表13 在基准LaSOT 上,与其他基于IoU 损失训练得到的满足不同IoU 阈值的测试集图像帧数占比的对比结果 (%)Table 13 Comparison results with other IoU-based loss for the ratio of frames exceeding different IoU thresholds on the test set of LaSOT (%)

表14 在基准GOT-10k 上,与其他基于IoU 损失训练得到的满足不同IoU 阈值的测试集图像帧数占比的对比结果 (%)Table 14 Comparison results with other IoU-based loss for the ratio of frames exceeding different IoU thresholds on the test set of GOT-10k (%)

最后,为了探讨中心偏差的正则项RS和光滑代理函数Aλ所带来性能上的影响,本文在GOT-10k 上对其进行了消融实验.表15 报告了不同消融的结果,其中LSIoU(w/oAR) 代表不具有正则项RS和光滑代理函数Aλ的损失,LSIoU(w/R) 代表配备了正则项RS而不采用光滑代理函数Aλ的损失,而LSIoU(w/Aλ) 代表采用了光滑代理函数Aλ而不配备正则项RS的损失.在本文λ取 1、2、4 和8 四个值以观察不同λ的影响.由表15 和图13 可以看出,正则项和代理函数提高了边界框回归损失的性能.其中对中心偏差的正则项可以较好弥补LSIoU在dH ＞2 时与IoU 不匹配带来的差异.同时也注意到,相较于正则项的加入,将中心偏差 (xΔ,yΔ) 的损失从ℓ1-norm 替换为光滑代理函数A2、A4和A8所带来的性能增益有限,其中可能的原因是不同于边界框尺寸的回归目标是动态的,边界框中心位置的回归目标是静态的,总是指向真值框的中心,也就是 (xΔ,yΔ) 的优化目标总是 (0, 0),但实际上中心偏差 (xΔ,yΔ) 很难回归到 (0, 0),因此对边界框中心位置的回归作光滑处理带来的增益较小.至于λ取值为 1 时,结果却逊于|x|,可能是因为Aλ(x) 与|x|的误差较大如图6 所示,所以λ取值适中即可,既不必取值太小使Aλ(x) 偏差 |x|较大,也不必取值太大使Aλ(x) 在原点处过于 “尖锐”而失去光滑的意义,本文不妨取值为2.

图13 在GOT-10k 上的成功率图Fig.13 Success plot on GOT-10k

表15 在GOT-10k 上,对 LSIoU 的正则项和代理函数的消融实验(%)Table 15 Ablation studies about the regulariztion and surrogate function on GOT-10k (%)

4 结束语

本文给出并证明了在回归过程中最优边界框参数之间满足的定量关系,提出了一种新的用于训练边界框回归的损失,即光滑IoU 损失.该光滑IoU损失不以IoU 损失作为基本损失,从优化散度的角度构造了全局光滑且极值唯一的损失函数,提出的光滑IoU 损失蕴含边界框各参数之间特定的最优关系,并将边界框参数作为一个整体进行回归,其唯一极值可使IoU 达到最优.该损失函数确保了在全局上可梯度下降更新参数,使得边界框更容易回归到极值处,从而规避了IoU 损失的固有缺陷.在采样数据上进行的大量实验表明,光滑IoU 损失和现有基于IoU 的损失方法相比,收敛速度更快,带来了显著的改进.光滑IoU 损失可以很容易地集成到当前基于IoU 损失的视觉任务模型中,本文将其应用在具有代表性的无锚框目标跟踪模型 Siam-FC++、SiamBAN 和 SiamCAR 上,在 LaSOT、GOT-10k、TrackingNet 和OTB2015 等主流测试基准上所取得的结果验证了光滑IoU 损失可以帮助提高边界框回归模块的性能.