水声射线传播的黎曼几何建模·基础理论*
郭肖晋 马树青 张理论 蓝强 黄创霞
1) (国防科技大学气象海洋学院,长沙 410073)
2) (长沙理工大学数学与统计学院,长沙 410114)
水声建模一般采用外嵌描述,即以欧氏空间固定坐标系等要素刻画水声信道.黎曼几何是弯曲空间上的内蕴几何学,更能反映流形的本质性质.水声学高斯波束模型借鉴自地震学,可有效避免传统射线追踪的弊端,在以Bellhop 为代表的水声模型中得到广泛应用,是水声射线建模与应用的主流方法之一.传统水声射线建模的欧氏空间底流形假设,难以有效刻画高斯波束的弯曲特性.本文通过建立水声射线传播的黎曼几何基本理论,得到程函方程、动态射线方程及高斯波束模型的黎曼几何内蕴形式,分析了水声射线几何拓扑性质,指出水声射线模型中的焦散点等价于黎曼几何中的共轭点,高斯波束几何扩展是测地线沿雅可比场的偏离,波束声线会聚体现为声场正截面曲率作用下偏离的测地线在共轭点的交汇.为验证理论正确性与适用性,本文以水平分层距离相关环境为例,给出特定环境和坐标系下应用前序理论建模的具体方法.3 个典型水声传播算例的仿真对比分析,表明水声传播黎曼几何理论模型是准确有效的,相比Bellhop 模型所采用的计算方法,具有更为清晰的数学物理含义.本文基础理论可方便推广至曲面、三维各向异性等情形,为后续在三维弯曲球体流形、四维时变伪黎曼流形等声传播环境下的黎曼几何射线建模研究奠定了理论基础.
1 引言
高斯波束一般被认为是波动方程的高频近似解,波束振幅在以射线轴为中心的横截面上服从高斯分布,被广泛应用于光学、地震学和声学等领域[1].水声学对高斯波束的机理研究较少,可分为欧氏空间近似计算和非欧几何建模尝试.
1.1 高斯波束的欧氏几何近似计算
高斯波束的数学描述可通过波动方程的抛物近似推导得到.Babich 和Lazutkin[2]最早利用抛物方程研究波动问题,给出了集中在射线附近、具有高斯波束形式的波动方程高频近似解.Červený等[3]将该结果推广至弹性动力学方程,提出了地震波波场的高斯波束近似计算方法.Porter 等[4]将上述地震波研究结果应用于声学中,首次给出了柱坐标下水声传播的高斯波束基本公式:
其中s为沿射线方向的弧长,n是距离中心声线的垂直距离,A为复常数,t(s)为沿声线的相位延迟,c,r和z分别代表声速、距离和深度,束宽W和曲率K表示为
p和q满足动态射线方程:
其中cnn是声速的二阶法向导数:
(2)式的初值条件为q(0)=iωW2(0)/2,p(0)=1,(1)式累加求得复合声压.在一定的假设下,q(s)≠0,Im(p(s)/q(s))≠0,∀s,高斯波束振幅在中心射线横截面上服从高斯分布,且(1)式在焦散线上仍然有效.由于高斯波束模型避免了经典射线在焦散区失效、本征声线计算不稳定性等问题,故基于高斯波束模型的Bellhop 软件在水声学中得到广泛应用.
高斯波束也可用傍轴射线近似法推导.傍轴射线近似法利用动态射线方程计算傍轴射线的振幅和相位,得到傍轴声压.Červený等[5,6]针对地震波,通过引入动态射线方程的复数解给出了傍轴射线近似法推导高斯波束的过程,因此该方法也被称为复动态射线追踪,所得结果与基于抛物波动方程的推导结果一致.Kravtsov 和Berczynski[1]详细比较了抛物波动方程方法、复动态射线追踪所导出高斯波束的异同,并指出Babich 和Lazutkin[2]的方法证实了复动态射线追踪及几何光学描述的衍射现象.
Smith[7]将Červený关于傍轴射线近似法和动态射线追踪的结果应用于水平分层距离无关的水声传播环境,分析了从傍轴射线至高斯波束的基本流程.设δq是二维平面内弧长s处沿着中心声线x法方向的无穷小距离(图1),T是走时,θ0是初始掠射角,δp=∂T/∂δq是δq的共轭动量.
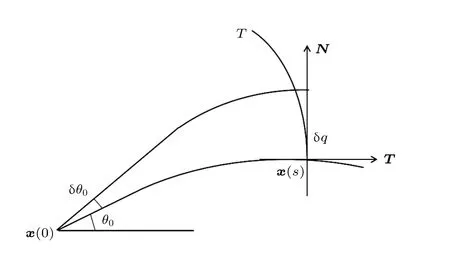
图1 傍轴射线示意图,是射线的切向量,N 是射线的法向量Fig.1.Paraxial ray tube, is the tangent vector,N is the normal vector.
基于Hamilton 原理和Hamilton-Jacobi 方程可知,Hamilton 主函数:
式中,cn是声速的一阶法向导数,相应的Hamilton正则方程为
对(3)式和(4)式更详细的叙述见文献[7].记θ0是二维 (r,z) 平面内声线x(s,θ0) 的初始掠射角,几何扩展q及其共轭动量p被定义为[5,7,8]
由(4)式容易得到几何扩展q及其共轭动量p满足动态射线方程(2)式.
对传播时间差二阶泰勒展开,可得到沿着中心声线x法方向距离δq处的传播时间差傍轴声线的相位差为 eiωδte.经典的傍轴射线近似法将傍轴射线的振幅简化为中心射线的振幅.可以看出,将动态射线方程(2)推广到复数解后,基于抛物波动方程法和傍轴射线近似法均可以得到高斯波束(1)式.
1.2 高斯波束的非欧几何建模研究较少
上述高斯波束研究均是基于欧氏几何描述.据爱因斯坦广义相对论理论,所有的物理现象都是物理客体在某种弯曲时空背景下的演化[9].介质的非均匀性决定了水声传播信道是弯曲的黎曼流形.研究非欧几何下的水声传播对于探索新型的水声建模方法、提高实际环境下计算准确性等具有重要意义.
当前黎曼几何建模研究多针对光传输或地震波传播开展.Gordon[10]指出发生在引力场和非均匀运动介质中的光学现象可以通过“光学度规”统一描述.郭弘等[11,12]从费马原理出发,建立了描写光束传播的几何量,将几何光学和波动光学合二为一地纳入三维黎曼流形之中.杨孔庆等[13]以走时函数为基础,给出了地震波传播的黎曼几何描述.
在水声领域,一些学者基于Lorentz 流形和Finsler 流形研究了超高速运动流体介质中的水声射线传播.基于声射线与Lorentz 流形(伪黎曼流形)测地线间的等价性,White[14]在1972 年提出了一种四维时空射线追踪的新方法,描述了运动流体介质中的声射线.1986 年,Meyer 和Schroeter[15]用Finsler 空间的测地线识别运动流体介质中的射线路径,得出与文献[14]相似的结果.在文献[14]的基础上,Bergman[16-19]认识到广义相对论中的测地线偏离方程(deviation equation)就是黎曼几何中的雅可比方程(Jacobi equation),首次将广义相对论中运用的黎曼几何理论迁移到水声学,研究了雅可比方程及共轭点理论在亚音速流体介质射线追踪中的应用,通过识别共轭点定位焦散点[20],分析了射线的稳定性.
上述文献基于Lorentz 流形和Finsler 流形给出了运动流体介质中射线和焦散点的追踪程序,但未研究黎曼几何在高斯波束法求解声场中的建模与应用.Smith[7]以传播时间为度规函数,证明了二维水平分层距离无关介质中动态射线方程的内蕴形式与测地线雅可比方程的等价性,给出了高斯波束模型的黎曼几何形式.应当指出,文献[7]仅研究了经典水声传播中相对简单的研究场景—水平分层距离无关环境,且在柱坐标系框架下建模,因而仅得到与现有声学文献等价的结论,其阐述偏重数学,未详细分析其几何与物理意义.
1.3 文章内容结构
本文利用测地线、雅可比场和共轭点等概念,建立径向对称情形下水声射线高斯波束黎曼几何模型的一般形式,揭示了水声场射线的拓扑性质,得到了一些新的水声学几何结论.首先给出了水声射线程函方程在黎曼流形上的广义形式-测地线方程,然后基于雅可比场理论建立径向对称情形下的高斯波束黎曼几何模型,分析了水声场射线的拓扑性质,再以水平分层距离相关情形为例,利用本文理论推导了该情形下高斯波束模型的黎曼几何形式,并通过3 个典型例子验证了理论结果的正确性.本文结果包含了文献[7]中考虑的水平分层距离无关情形,且所得结果是内蕴的,与坐标系选取无关,为在实际弯曲流形下开展水声建模与计算提供了理论基础.
2 水声测地线程函方程
介质的天然非均匀性决定了水声传播信道是一个弯曲的黎曼流形.最小作用量原理表明,水声射线总是沿着传播时间最短的方向传播.测地线是欧氏空间的直线在黎曼流形上的推广.当以传播时间作为流形的度规结构时,黎曼流形上的测地线方程是欧氏空间水声射线程函方程的广义形式.本节建立黎曼流形上的水声测地线程函方程,该方程对于欧氏空间仍适用.
2.1 传播时间的黎曼度规
黎曼度规是微分流形上对称、正定且光滑的二阶协变张量场[21],刻画了流形上向量的长度、夹角和曲线的弧长等,是计算流形上曲率、测地线等几何量的基础.水声射线在水声信道空间中传播,可以用黎曼几何方法进行描述,定义黎曼流形 (M,g)表示水声传播信道,是流形M的局部坐标系.采用爱因斯坦求和法则,黎曼度规g表示为[21]
仅由黎曼度规决定的性质称为流形的内蕴性质,(8)式与流形嵌入欧氏空间的方式、坐标系的选择及曲线参数变换均无关.在实际问题中,可以选用适宜的坐标系对具体的海洋环境进行建模分析.
2.2 测地线程函方程
黎曼流形 (M,g) 的测地线方程即流形上的水声射线程函方程.走时T(x) 为曲线x(σ) 的泛函,走时T(x) 最短的极值条件要求——Lagrangian 函数:
满足Euler-Lagrangian 方程:
由此可得,自然参数t下测地线方程为[22]
其中,是Christoffel 联络系数,计算公式为
测地线方程(10)是欧氏空间中水声射线程函方程在黎曼流形的推广,该方程对于欧氏空间仍然适用.
3 高斯波束的黎曼几何模型
高斯波束法[3-5]是当前的声场计算模型之一,经典的高斯波束模型基于欧氏几何建立.黎曼几何中的雅可比场是沿测地线的变分向量场,刻画了周围测地线与中心测地线的分离速率,是声线几何扩展的自然描述,雅可比场由雅可比方程描述.本文基于雅可比场理论计算傍轴声线的振幅和相位,给出径向对称情形下动态射线方程和高斯波束模型的黎曼几何一般描述.
3.1 测地线的雅可比方程
首先给出雅可比场的数学定义及其分量函数满足的雅可比方程.设光滑曲线x(t),t ∈[0,a] 是黎曼流形 (M,g) 上的一条测地线,H:[0,a]×(-ε,ε)→M是x(t),t ∈[0,a] 的测地变分,即对所有的u ∈(-ε,ε) ,H(t,:): [0,a]→M是测地线.若H(t,u0)=x(t),则沿测地线x(t) 的 雅可比场Y(t) 为[21]
由此可得雅可比场Y(t) 分量函数满足的方程:
3.2 几何扩展的雅可比场描述
为了刻画几何扩展的内蕴性质,可自然定义=δq/c为距离δq对应的传播时间,其由流形M的度规g决定,不随流形的嵌入方式和坐标系的变化而改变,因而δq˜ 是内蕴变量.记δ=∂T/为的共轭动量.可定义内蕴几何扩展:
设x(t,θ) 是二维平面内从声源处发出的以时 间t为参数的声线(测地线),θ为 掠射角,映射f(t,θ)=x(t,θ).根据雅可比场的定义(12)式可知:
是变分f沿声线x(t,θ0) 的雅可比场.记x(t)=x(t,θ0),取单位正交标架场:
二维截面 [u ∧v] 的截面曲率K(u,v) 定义为[21,23]
又因〈e1,e1〉=〈e2,e2〉=1,〈e1,e2〉2=0,故有:
结合(17)式,有:
取雅可比场的初值为Y(0)=Y1(0)e1(0),则〈Y(0),(0)〉=0,由Gauss 引理可知,雅可比场Y与中心声线x的切向量处处正交,即Y2(t)≡0,∀t.于是雅可比场Y(t)=Y1(t)e1(t).由内蕴几何扩展的定义(14)式、雅可比场的定义(15)式、(16)式及几何含义,可以推导出,雅可比场Y(t) 在法方向的分量:
因此,测地线的雅可比场是射线几何扩展的自然描述,雅可比方程:
对于一族具有公共端点的测地线,此时Y(0)=0,雅可比场Y(t) 关于参数t的变化刻画了这族测地线的“发散性”或“收敛性”,若雅可比场的模长|Y(t)| 沿 着测地线是关于参数t的增函数,则该测地线附近的测地线是发散的;若存在沿测地线x(t) 的雅可比场Y(t),满足Y(0)=Y(tk)=0,则称x(tk)是x(0) 沿测地线x(t) 的的共轭点[21,23],此时测地线x(t) 周围的测地线在共轭点x(tk) 附近收敛.水声学中的焦散点指射线束外嵌几何扩展为0 的点[8].由于内蕴几何扩展q˜(t)=Y1(t),故水声学中的焦散点等价于黎曼几何中的共轭点.
3.3 水声射线几何拓扑性质的雅可比场理论分析
截面曲率是Gauss 曲率在高维流形的推广,一定程度上反映了流形的拓扑结构.截面曲率对大范围测地线性质的影响一直是黎曼几何的重要研究课题,取得了丰富的研究成果[21,23].在3.2 节中,已经给出了截面曲率的定义,并看到了其在雅可比方程中的作用.本节利用一些几何结论揭示水声场射线的拓扑性质,分析截面曲率对于声线“收敛性”和“发散性”的影响.
根据Cartan 等距定理[24],当截面曲率K为正常数时,黎曼流形 (M,g) 等距同胚于半径为的标准球面;当截面曲率K为0 时,黎曼流形(M,g) 等距同胚于欧氏空间;当截面曲率K为负常数时,黎曼流形 (M,g) 等距同胚于双曲空间.
由雅可比方程(19)可以看出,声线x(t) 的雅可比场由截面曲率K决定.当K为常数时,黎曼流形(M,g) 为常曲率空间,此时初值问题(21)有解析解:
当截面曲率K为常数时,分析雅可比场的分量Y1(t) 的解析解(22)可知:
1) 如果常截面曲率K>0,若,则Y1(tk)=0,k=1,2,···,∞.声线x(t) 周期性地产生焦散点,x(t) 周围的声线在x(tk) 附近收敛,K的值越大,产生焦散点的频率越高.
2) 如果常截面曲率K≤0,那么声线x(t) 周围的声线是发散的,其中K=0 时Y1(t) 线性增长,K <0 时近似为指数发散,此时不会产生焦散点.
当截面曲率K不固定为常数时,通过黎曼几何中的共轭点定理[25],能够刻画一般情形下截面曲率对共轭点的影响.
可以看出,利用雅可比场描述水声射线高斯波束的几何扩展能够揭示水声射线的几何拓扑性质,本文分析并给出了焦散问题的数学解释.
3.4 高斯波束的振幅与相位
前文已经指出测地线的雅可比场刻画了声线的内蕴几何扩展(t) ((t)=Y1(t)),雅可比方程(21)给出了雅可比场Y1(t) 的求解方法.本节利用雅可比场和雅可比方程给出高斯波束的振幅和相位的内蕴表达.
经典射线法利用射线级数得到亥姆霍兹方程的近似解,即射线的声压场:
设W为单位立体角内的辐射声功率,θ0为初始掠射角,射线管内的能量是守恒的,因此单根声线声强的基本公式为
若不计入常数因子,声压幅值:
由(23)式可得:
上式给出了单根声线路径的声压.与经典高斯波束法等价.需要指出,本文将射线束的振幅简化为中心声线的振幅(24),未更深入地考虑傍轴振幅[26].
将雅可比方程(21)的解推广到复数域上,此时传播时间差δte是复值,中心声线附近的声线是复声线,在/Y1虚部不为0 的假设下,波束(26)的振幅满足高斯分布,称为高斯波束.此外,根据动态射线方程(2)可知,传播时间差,这说明利用雅可比场建立高斯波束模型是正确的.测地线方程(10)、雅可比方程(21)和高斯波束(26)给出了径向对称情形下高斯波束法求解声场的黎曼几何形式,完善了高斯波束模型的数学基础,揭示了高斯波束在黎曼几何意义下的特征属性,为弯曲流形上的声场计算提供了理论基础.
4 距离相关水声环境下的高斯波束黎曼几何模型
本节导出声速剖面水平分层距离相关情形经典水声射线高斯波束模型的黎曼几何形式,并与现有结果进行对比.
4.1 水声射线的走时场
设 (r,ϕ,z) 是三维欧氏空间的柱坐标系,x(t)=(r(t),ϕ(t),z(t))T是柱坐标系下的射线轨迹,参数t是传播时间.假设海水深度为H(m),海面边界为za=0 m,海底边界为zb=H(m).声源在z轴上(r=0,ϕ=0).经典水声射线理论假设波导为柱体:
其中R是地球半径.
设c(r,z) 是水平分层距离相关的声速剖面,假设声速剖面c(r,z) 及其一阶偏导数∂c/∂r和∂c/∂z是连续可微的.由于三维欧氏空间 R3的线元:
(27)式和(28)式给出了柱坐标系下射线走时函数的几何描述,即水声学教材[8,27]中传播时间方程.
4.2 水声射线方程
由此可以给出黎曼流形 (N,) 的测地线(射线)方程:
设θ0为初始掠射角,那么射线方程(29)的初值条件为
利用 ds=cdt,可以将射线方程(29)用弧长 ds参数化为
应当指出,弧长参数化后的射线方程(31)与水声学教材[8,27,28]中通过程函方程推导的射线方程是一致的.
4.3 雅可比方程与高斯波束
和(11)式,有:
因此可得:
结合(21)式和(32)式,可以得到:
在水平分层距离无关介质(cr=0)中,雅可比方程为
根据高斯波束的内蕴形式(26)可知,掠射角为θ,距离中心射线的垂直距离为δη时高斯波束的声压为
由(2)式和(14)式可以得到柱坐标系下经典动态射线方程的内蕴形式为
和的定义见(14)式.对时间t的二阶导数满足
可以看出,经典动态射线方程的内蕴形式(37)等价于雅可比方程(33).
因此,通过第2 节与第3 节相关理论,能够给出水平分层距离相关环境下的程函方程、动态射线方程及高斯波束模型,经分析发现与经典水声学理论的结果一致,从而可进一步验证本文理论的正确性.同时,本文所给出的方程是内蕴形式,与坐标系选取无关,对径向对称的其他声传播问题仍适用.此外,本文说明水声学中的声线焦散现象与黎曼几何中的截面曲率、雅可比场、共轭点等几何量相关,为后续研究深海会聚区等物理现象提供了理论基础.
4.4 数值仿真
本节通过采用若干经典声速剖面环境,编写程序对前文建立的黎曼几何模型进行仿真,并与Bellhop 的射线求解结果进行了对比验证.
4.4.1 双曲余弦声速剖面
双曲余弦声速剖面c(z)=c1cosh(z-z1)/E的截面曲率:
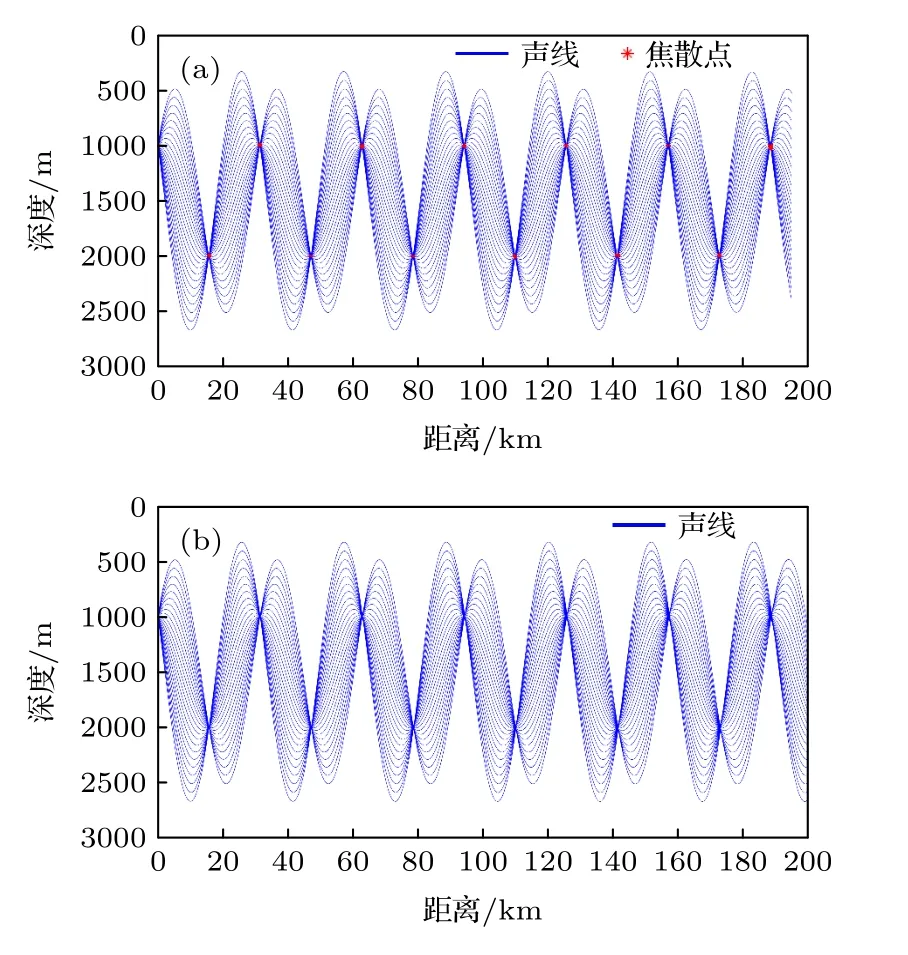
图2 双曲余弦声速剖面的声线和焦散点,参数为c1=1500 m/s,z1=1.5 km,E=5 km,声源深度为z0=1 km,初始掠射角 θ0 ∈(-10°,12°),t ∈[0,130]s (a)共轭点理论仿真结果;(b) Bellhop 仿真结果Fig.2.Rays and caustics for the hyperbolic cosine sound speed profile with parameters c1=1500 m/s,z1=1.5 km,E=5 km,z0=1 km,θ0 ∈(-10°,12°),t ∈[0,130]s : (a)Conjugate point theory simulation results;(b) Bellhop simulation results.
4.4.2 线性声速剖面
线性声速剖面c(z)=c0+bz(b≠0) 的截面曲率K=cc′′-(c′)2=-b2<0, 此时黎曼流形 (N,)等距同胚于双曲空间.根据(22)式,|Y1(t)| 是关于t的单调递增函数,不会产生共轭点.因此任意声线x(t) 周围的声线都是发散的,不会产生焦散点.图3(a)和(b)分别表示通过共轭点理论和Bellhop的射线仿真结果,可见求解结果一致且声线指数发散,不会产生焦散点,与理论结果吻合.

图3 线性声速剖面的声线求解结果,参数为 c0=1500 m/s,b=-0.01,声源深度为 z0=1 km,初始掠射角 θ0 ∈(-5°,-2°),t ∈[0,25]s (a)共轭点理论仿真结果;(b) Bellhop 仿真结果Fig.3.Rays for the linear sound speed profile with parameters c0=1500 m/s,b=-0.01 ,z0=1 km,θ0 ∈(-5°,-2°),t ∈[0,25]s : (a) Conjugate point theory simulation results;(b)Bellhop simulation results..
4.4.3 深海高斯涡模型
考虑存在高斯涡的深海结构,声速剖面为
其中η=2(z-1000)/1000,DC 为涡强度,DR 是涡的水平半径,DZ 是涡的垂直半径,Re 是涡心的水平位置,Ze 是涡心的垂直位置,声速等值线见图4.

图4 声速剖面(38) 的声速等值线,参数为 DR=150 km,DZ=500 km,Ze=1000 km,Re=300 kmFig.4.Sound speed contours for the sound speed profile (38) with parameters D R=150 km,DZ=5 00km,Ze=1000 km,.
声速剖面(38)下的截面曲率不恒为常数,不能直接得到雅可比方程(33)的解析解.本文选取20 根声线,利用四阶Runge-Kutta 法计算声速剖面(38)下测地线方程(29)和雅可比方程(33)的数值解,截面曲率和雅各比场的数值求解结果见图5,进而得到声线和焦散点(图6(a)).参数设置为r(0)=0 m,z(0)=400 m,掠射角θ0∈[-10°,10°],时间t∈[0,320] s.
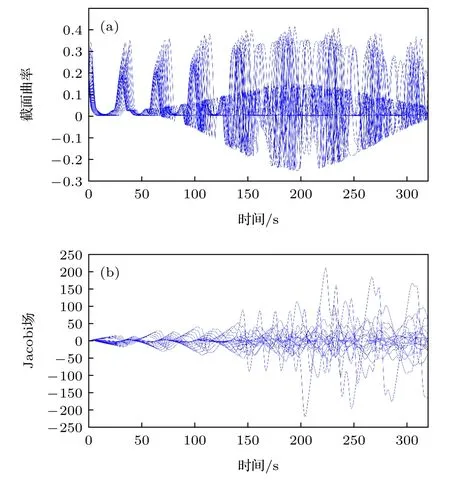
图5 声速剖面(38)的截面曲率K 和雅可比场Y1(t)仿真结果 (a) 截面曲率K 仿真结果;(b) 雅可比场Y1(t)仿真结果Fig.5.Section curvature K and Jacobi field Y1(t) for the sound speed profile (38): (a) Section curvature K simulation results;(b) Jacobi field Y1(t) simulation results.
Bellhop 是当前主流的射线求解软件之一,可实现高斯波束法求解声场,但无法直接计算焦散点位置.本文利用雅可比方程刻画声线的内蕴几何扩展,能够更便捷地计算声线的焦散点(图6(a)).在仿真参数不变的情况下,声速剖面(38)的Bellhop的声线仿真结果见图6(b).结果显示,采用黎曼几何模型计算的声线结果与Bellhop 一致,这说明本文的仿真计算方法是可行的.

图6 声速剖面(38)的声线和焦散点 (a)共轭点理论求解结果;(b) Bellhop 射线求解结果Fig.6.Rays and caustics for the sound speed profile (38):(a) Conjugate point theory simulation results;(b) Bellhop simulation results.
5 结论
本文采用黎曼几何建立了高斯波束模型的内蕴形式.主要工作如下:
1)基于最小作用量原理,在水声射线走时黎曼度规下,给出了黎曼流形上的水声测地线程函方程;
2)利用雅可比场理论建立了一般径向对称声传播环境下的高斯波束黎曼几何模型,揭示了水声场射线的拓扑性质.
在黎曼几何框架下,本文利用测地线、雅可比场和共轭点等概念给出了射线高斯波束的几何解释.在传播时间的黎曼度规下,水声程函方程等价于黎曼几何中的测地线方程,高斯波束的内蕴几何扩展对应于测地线沿雅可比场的偏离,焦散点等价于共轭点.这种等价性使水声射线高斯波束模型具备了黎曼几何意义.本文研究为在实际弯曲底流形下开展水声建模与计算提供了理论基础.后续可开展考虑地球曲率的远程声传播建模理论、深海会聚区建模应用等相关研究工作.
感谢宋君强院士对该探索研究的鼓励和支持,黄思训教授、梁湘三教授审阅论文初稿,特致谢忱.

