BrF 分子电磁偶极跃迁转动超精细微波谱模拟*

陈润 邵旭萍 黄云霞 杨晓华

(南通大学理学院,南通 226019)

本文推导了BrF 振动基态(X1∑,v=0)下J=1←0 的转动超精细光谱的跃迁偶极矩,总结了跃迁选择定则为: ΔJ=±1;ΔF1=0,±1 和ΔF=0,±1;而且,当ΔF1=ΔF 时谱线强度很强,反之很弱.当能级之间存在微扰相互作用时,某些谱线由电偶极和核磁偶极跃迁共同产生,然而磁偶极仅仅贡献大约十亿分之一的光谱强度.计算所得光谱线宽和相对强度与实验结果一致.同时,在|JI1F1I2F 〉基矢下对Hamilton 量矩阵对角化确定了转动超精细光谱的位置,与实验误差小于1/50 谱线宽度(＜10—8).最后模拟了微波转动超精细光谱,所得结果有助于超精细分子光谱实验和其他相关应用研究.

1 引言

原子和分子光谱学在许多方面有重要应用,如原子和分子结构研究[1]、精密测量[2,3]、以及寻找电子电偶极矩(eEDM)[4-6]、验证精细结构常数[7,8]可能随时间的变化等相关应用[9,10].原子分子的超精细结构,通常掩盖于Doppler 背景之中,只有采用冷却方法才能加以观测.传统的制冷手段为超声束膨胀技术,可以将样品冷却至1 K 量级.然而,该技术所获得的冷却温度不足够低、样品的吸收长度短、样品浓度起伏较大.这些缺点使得其难以满足现代原子分子光谱学及其应用的需求.近几十年来,现代冷原子和冷分子物理[11-18]的飞速发展,为原子分子的超精细结构的精确研究提供了坚实的研究平台,使得我们可以同时进行超高分辨率、超高精度和超高灵敏度的光谱研究,赋予了原子和分子光谱学新的生命.

超精细光谱可揭示原子分子内的弱核相互作用,与价格不菲的核物理方法相比,通过原子分子光谱学获得核内信息更为经济.相较于分子冷却的深入研究,冷分子光谱的研究还相对较少.另一方面,冷分子光谱学[11,13-18]所获得的精确的分子超精细结构,对于冷分子的诸如碰撞、操控、进一步冷却乃至最终实现分子玻色-爱因斯坦凝聚(BEC)等也至关重要.这就是说,分子超精细结构的研究,也将促进冷分子物理及其应用研究的发展.

碱金属双原子冷分子在实验和理论上都取得了许多研究成果[19-23].然而,它们的化学性质不稳定,尽管采用外加电场可以在一定程度上抑制这种化学反应[24],但这仍影响碱金属冷分子的各种应用.卤素异核极性分子化学性质稳定,在冷分子领域必然会有更广泛的应用,而且采用近共振红失谐激光辅助Stark 减速[25-27]将等效温度降至1 mK量级.在卤素双原子分子中,BrF 的研究最少.最早由Smith 等[28]于1950 年报道了微波区J=1←0的超精细光谱,后来Calder 等[29]提高了分子常数的精度.Nair 等[30]进一步研究了BrF 的振动基态内J=1←0 和J=2←1 跃迁的超精细光谱,并获得了分子电偶极矩和核电四极矩.此外,Clyne 等[31]使用激光感应荧光光谱技术观测并分析了BrF 的B3∏0+←X1∑+吸收光谱.

本文在角动量耦合矢下,写出了超精细结构的Hamilton 量矩阵,进而计算了BrF 电子振动基态下的转动超精细能级,推导了转动超精细跃迁偶极矩,包括电偶极矩和核磁偶极矩,最终模拟了其转动超精细光谱.

2 理 论

2.1 谱线位置

谱线位置由跃迁的超精细能级决定.超精细结构主要来源于核磁偶极作用和核电四极作用.转动超精细Hamilton 量由转动项和超精细项组成[32]:

其中Bv是转动常数;Dv是其离心畸变常数;J为除核自旋外的总角动量;T2(∇E)和T2(Qi)分别是核外电子在核处的电场梯度二阶张量和核电四极矩的二阶张量,其中下标i=1 或2 代表原子Br 或F;I为核自旋;C1和C2为核自旋-分子转动耦合常数,C3和C4为核自旋-自旋张量和标量耦合常数.

Br(79Br 和81Br)和F 原子的核自旋分别为3/2和1/2.因此,角动量耦合顺序为: 分子除核自旋外的角动量J与核自旋较大的Br 原子I1耦合成F1,F1再与F 原子核自旋I2耦合形成总角动量F.即,F=F1+I2,其中F1=J+I1.本文以|JI1F1I2F〉为基矢,对角化Hamilton 量矩阵得到BrF 分子的转动超精细能级,从而获得跃迁谱线的位置.超精细结构Hamilton 量矩阵元的转动及两核电四极矩部分详细表达式见文献[33]的(6)式、(8)式和(9)式;而本文(2)式中增加了C2,C3与C4相互作用,因此,转动-核自旋和核自旋-自旋相互作用为

2.2 光谱强度与线型

2.2.1 电偶极跃迁

其中约化矩阵表示分子坐标系向实验室坐标系的转换,可写为

其中q=—1,0,1 表示J在实验室坐标系Z轴上的三个投影,()和{}分别是Wigner 3-j和6-j符号.

2.2.2 磁偶极跃迁

类似地,可以得到磁偶极约化矩阵:

所以,总的核磁偶极跃迁矩:

2.2.3 电偶极与磁偶极混合跃迁

根据跃迁宇称选择定则,电偶极跃迁发生于宇称不同的态之间,而磁偶极跃迁发生于宇称相同的态间[35],其中宇称p=(—1)J.原则上,光谱跃迁由电偶极或磁偶极跃迁两者之一导致.但是,当一个量子态是由微扰引起的两个宇称相反的无微扰量子态的叠加时,电偶极和磁偶极跃迁就会同时发生.此时,总偶极跃迁矩为电偶极和磁偶极跃迁矩的和:

当电偶极跃迁矩或磁偶极跃迁矩其中之一为0 时,公式(10)也同样适用.转动超精细跃迁概率与跃迁偶极矩的平方成正比.因此,可以获得转动超精细跃迁选择定则和光谱相对强度.

2.3 线 型

转动超精细光谱只有在其他光谱展宽被大幅抑制时才能观察到.通常情况下,可以通过各种方法将样品冷却,例如以前的超声分子束膨胀或现代分子冷却技术可将样品冷却到1 K 甚至更低的温度[16-19].此时,自然增宽占主导,光谱线型近似为Lorentz 线型,线宽为

这里,ν为谱线频率,h为Planck 常数,c为真空中的光速.

3 结果与讨论

3.1 谱线位置

根据2.1 节所述,通过求解Hamilton 量矩阵可获得转动超精细能级,如图1 所示,这里令J=0 转动能级(不考虑超精细结构)的能量值为0.本文计算所需分子常数主要来源于文献[37],总结列于表1 中.

图1 79BrF(上)和81BrF(下)振动基态(X1∑,v=0)下的超精细能级.图中还标明了各能级的能量值和量子数Fig.1.Hyperfine-rotation energy levels of 79BrF (upper) and 81BrF (lower) in the vibronic ground state (X1∑,v=0).The quantum numbers and the values of the levels are labeled as well.

表1 BrF(X1∑,v=0)分子常数Table 1.Molecular parameters of BrF(X1∑,v=0).

转动超精细跃迁谱线的频率可通过计算转动超精细能级之差获得.然而,并非任意两能级间的跃迁都存在,这将在3.2 节中讨论.表2 列出了转动超精细光谱及其与实验值[37]的偏差.对于79BrF和81BrF,计算总体方差分别为0.4 kHz 和0.1 kHz,均约为1/50 谱线线宽,即相对误差在10—8内(在实验误差范围内与实验观测值完全一致),这说明我们的方法是可靠的.此外,我们最初认为核自旋-自旋相互作用相对于分子转动-核自旋相互作用很小,其仅仅对谱线的位置有微小的影响,然而进一步计算发现,其还会改变谱线的频率顺序.因此,为了准确模拟转动超精细光谱,核自旋-自旋相互作用不可忽略.

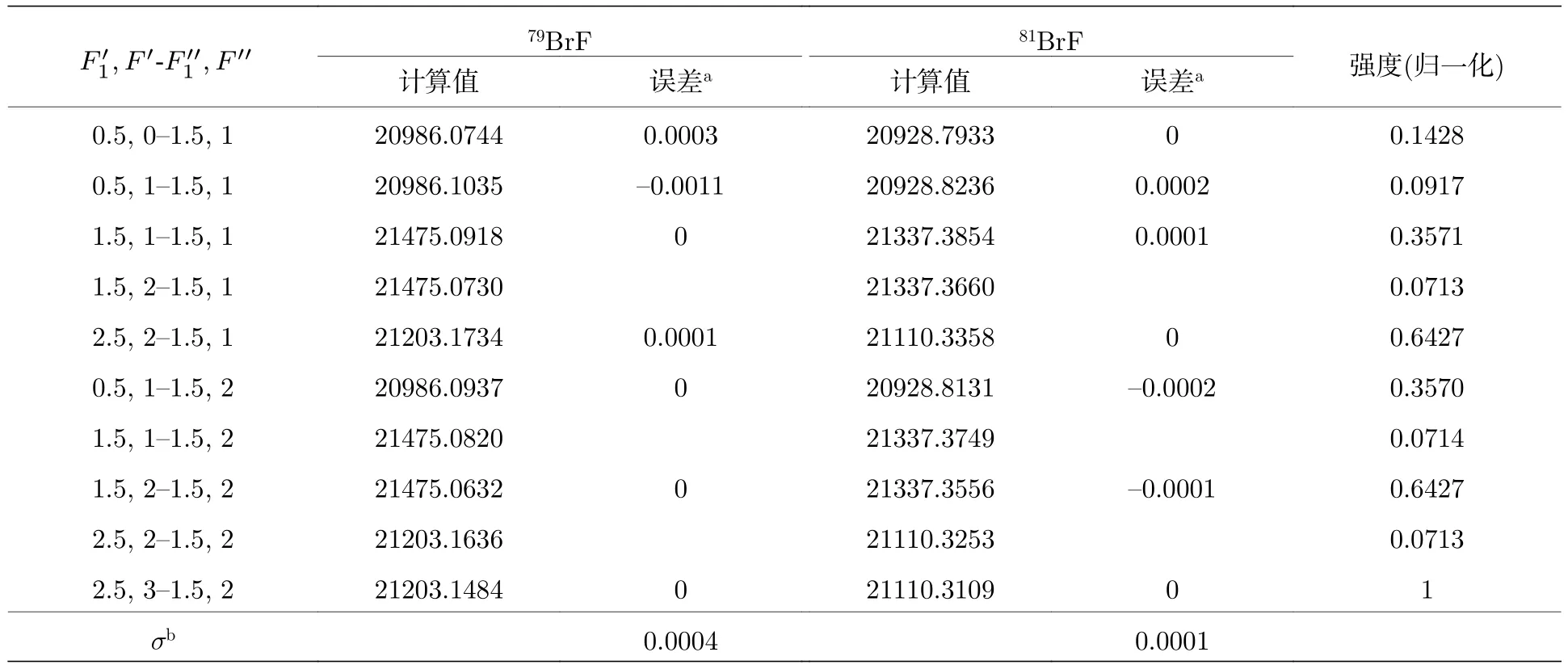
表2 BrF 分子振动基态(X1∑,v=0)中J=1←0 跃迁的转动超精细光谱计算值(单位: MHz),同时列出了其与实验值的偏差和归一化光谱强度Table 2.Calculated hyperfine-rotation spectra (in MHz) of the J=1←0 transition in the vibronic ground state (X1∑,v=0) of BrF molecule.Deviations (in MHz) from the experimental spectra and the normalized intensity are listed as well.

3.2 谱线强度与线型

根据2.2.1 和2.2.2 节可以分别获得电偶极和核磁偶极跃迁矩,其中有四组跃迁的电偶极跃迁矩和磁偶极跃迁矩均不为0,这是由能级之间的微扰所导致的.微扰导致跃迁谱线的上、下态中的一个或两个,由两个相反宇称态混合而成.通过对量子态Hamilton 量矩阵的深入研究,可以获得微扰细节.其转动超精细态的Hamilton 量矩阵为

详情可参阅文献[33].因此,态|J,F1,F;p〉=|0,1.5,1;+〉由非微扰的|0,1.5,1;+〉0与|1,1.5,2;— 〉0和|1,2.5,2;— 〉0混合而成;|0,1.5,2;+〉由非微扰的|0,1.5,2;+〉0与|1,1.5,1;— 〉0和|1,0.5,1;— 〉0混合而成.可见微扰导致电偶极子和磁偶极子同时参与谱线跃迁,而共同贡献于谱线强度.

如2.2 节所述,在1 K 或更低的温度下才能观察到转动超精细光谱.在这种温度下,其他光谱展宽可忽略,光谱线型主要由自然展宽决定.根据(11)式中描述的跃迁概率,本文计算出0.5,0-1.5,1 的线宽为15.6 kHz,其电偶极跃迁矩de=0.39 a.u.(原子单位).核磁偶极跃迁概率其中α为精细结构常数.可见核磁偶极跃迁仅贡献了十亿分之一的光谱强度,与电偶极跃迁相比,核磁偶极跃迁贡献很小,几乎无法通过实验观测到.

表3 列出了转动超精细跃迁偶极矩.因此,我们可以总结出转动超精细跃迁选择定则为: ΔJ=±1;ΔF1=0,±1 和ΔF=0,±1;而且,当ΔF1=ΔF时谱线强度较强,反之则很弱.归一化的光谱强度也列于表2 中,其中三条谱线0.5,1-1.5,2,0.5,0-1.5,1 和0.5,1-1.5,1 的相对强度与文献[37]的图1 中的实验光谱一致.这说明我们所计算的光谱相对强度是基本正确的.

表3 BrF 振动基态下的转动超精细跃迁偶极矩Table 3.Hyperfine-rotation transition dipoles of BrF within its vibronic ground state.

3.3 光谱模拟

图2 给出了BrF 振动基态(X1∑,v=0)下J' -J''=1—0 转动跃迁的超精细光谱,上图和中图分别代表79BrF 和81BrF.由于丰度差异很小,两种同位素的强度也几乎相等.考虑到其他可能存在的弱展宽因素,例如碰撞和光谱仪展宽,将光谱线宽设置为18 kHz.图中画出了10 条谱线,并标记为-,F''.如图2 所示,谱线1.5,1-1.5,2,1.5,2-1.5,1和2.5,2-1.5,2 的相对强度极小,导致它们几乎无法观测,如图中蓝色圆圈所示.因此,BrF 振动基态(X1∑,v=0)下J' -J''=1—0 转动跃迁的超精细实验光谱仅呈现7 条谱线,这与文献[37]的实验结果完全一致.

图2 BrF 振动基态(X1∑,v = 0)下J=1←0 转动超精细跃迁光谱模拟(下图),红线代表79BrF,黑线代表81BrF.两同位素丰度相差很小,使得它们的光谱强度几乎相等.超高分辨的光谱模拟见上图(79BrF)和中图(81BrF),其中,谱线1.5,1-1.5,2,1.5,2-1.5,1 和2.5,2-1.5,2 的相对强度极小,导致它们无法观测到(蓝圈部分)Fig.2.Simulated hyperfine-rotation spectra (lower) of the J=1←0 transition within the vibronic ground state (X1∑,v= 0) of BrF of its two isotopes,79BrF in Red and 81BrF in black.Their spectral intensities are almost the same accordingly due to their nearly equal natural abundance of the two isotopes.Details of the spectra of 79BrF (upper) and 81BrF (medium) of the unresolved spectra(lower) are plotted as well.Intensities of the spectra F1,F=1.5,1—1.5,2,1.5,2—1.5,1 and 2.5,2—1.5,2 are too small to observe,as shown in the blue circles.

光谱实验研究过程中,光谱谱线标识是一项复杂而耗时的工作,是研究能否顺利进行的关键.对于分子振转光谱来说,谱线频率的二次逐差近似常数、谱线强度随J值的Boltzmann 分布等特点,可以作为重要的标识参考指标[38].但是,转动超精细光谱几乎没有规律可循,因此光谱的理论模拟对于其谱线标识尤为重要.本文基于实验分子常数模拟所获得的转动超精细光谱,谱线频率偏差仅约0.4 kHz (1/50 谱线线宽)、谱线频率位置和相对强度与实验一致,完全可以作为实验谱线标识的依据.基于实验分子常数所获得的谱线位置的准确性,似乎是理所当然的,然而相对强度也是谱线标识的另一个重要参考指标.对于“全新”分子,没有可用的精确的实验分子常数,可以利用量化计算的方法(例如MOLPRO 程序计算)先获得相对精确的分子常数,然后采用本文的方法预测谱线的频率位置.尽管预测的谱线频率位置可能不够精确,但模拟谱线的模式(谱线间隔、顺序及相对强度)可以作为光谱标识的参考,从而大大提升研究效率.

4 结论

本文在|JI1F1I2F〉基矢下,采用标准角动量理论推导了BrF 转动超精细跃迁偶极矩,并总结了跃迁选择定则.同时,通过Hamilton 量矩阵的对角化计算了超精细能级,进而获得了谱线的频率位置.最后,模拟了BrF 分子电子振动基态中的转动超精细光谱,其中光谱频率位置与实验误差约为1/50 谱线线宽、相对强度与实验一致.研究结果表明,核磁偶极跃迁对光谱强度贡献仅为7.71×10—9,远小于电偶极跃迁贡献,实验难以观测.此外,我们研究发现核自旋-自旋相互作用导致转动超精细光谱的频率位移,尽管对标识可能影响不大,但其会改变谱线频率顺序,因此必须加以考虑.对于“全新”无实验光谱数据的分子而言,采用量化计算获得相对精确的分子常数,再借助本文的方法模拟转动超精细光谱,可以很好地指导实验光谱的标识工作.本文结果还对其他相关应用(例如超冷分子的单个超精细态[39]制备)具有很好的参考意义.

感谢Durham 大学的Jeremy M.Hutson 教授和Louisville 大学刘进军教授关于跃迁偶极矩的有益讨论.