对称分子 H2+ 在强短波激光场中高次谐波椭偏率性质的研究*

于术娟 刘竹琴 李雁鹏

(延安大学物理与电子信息学院,延安 716000)

通过数值计算,研究了强短波(4 00—600 nm)激光场中 分子高次谐波辐射的椭偏率性质.研究表明, 分子在不同激光强度、不同激光波长、不同核间距及不同取向角下高次谐波的椭偏率性质是不同的;特别是在两中心干涉区,激发态在高次谐波产生中起着重要作用,但在不同取向角下,激发态对谐波椭偏率的影响不同;分析表明,这些不同的影响源于沿平行和垂直于激光偏振方向辐射的高次谐波的相对产量,以及激发态对平行和垂直谐波产量的影响;此外,椭偏率的测量检验了强场近似和平面波近似在强短波激光场中是成立的,并对强短波激光场中分子动力学做了更充分的研究.

1 引言

当原子或分子暴露于强激光场中时,库仑势被电场严重扭曲.因此,电子可通过隧穿从原子核中脱离,脱离的电子在激光场中进行加速运动,当激光场改变方向时,电子再次返回原子核,进而被原子核俘获,并伴随着高能光子的释放,这个过程称为高次谐波产生.由于高次谐波可用作阿秒脉冲光源,近年来,学者们越来越关注高次谐波辐射的研究[1-3],并提供了一种独特的方式来探测物质在超快时间尺度上的结构[4,5]和电子动力学[6,7].

高次谐波产生的物理过程可通过三步模型[8]和列文斯坦模型[9]来理解,模型中有两个重要的假设,即强场近似.首先,只有基态对系统的演化起重要作用;第二,当电子脱离原子核时,忽略库伦势的影响.这些假设适用于具有Keldysh[10]参数强的低频激光场,其中,是有质动能,Ip是原子的电离能,E和ω0分别是激光的振幅和频率,因此,在低频激光场中隧穿图像和平面波近似都是成立的.

以往学者们主要关注沿激光偏振方向辐射的高次谐波功率谱,最近,准直对称分子在低频激光场中谐波的椭偏率问题成为学者们关注的焦点,例如[11,12]和 N2[13-15];根据实验和理论研究结果,在线偏振激光场作用下,准直分子可以产生谐波的椭圆偏振态,而谐波椭偏率的起源是多电子效应[13]、库伦效应[15]、两中心干涉效应[11]以及电子运动的量子不确定性[16].随后研究了不对称分子谐波的偏振性质[17-22],理论研究表明,由于最高占据分子轨道的不对称性,在 C O 的高次谐波产生中可观察到大的椭偏率[20,21];由于不同高次谐波产生路径间的相互作用,在 H eH2+的谐波产生中也可观察到大的椭偏率[22];同时圆[23]、椭圆[24]和正交[25,26]偏振激光脉冲驱动高次谐波产生的椭偏率一直也是实验和理论上的研究热点.以前主要研究强的低频激光场中谐波的椭偏率问题,但在强的高频激光场中(Keldysh 参数γ接近或略大于1),谐波的椭偏率未被研究过,由于高次谐波的椭偏率不仅与平行谐波及垂直于激光偏振方向发射的谐波(即垂直谐波)密切相关,还与高次谐波的相位密切相关,为研究高频激光场中分子高次谐波的产生提供了深入的见解;另外,高频激光场中电子的动力学非常复杂,激发态效应非常强[27],激发态对谐波发射的影响已被研究过[28-30];且激发态在平衡核间距及大核间距附近对低频激光场中高次谐波谱上干涉最小的影响也被研究过[31];目前的研究表明,当Keldysh 参数γ≈1 时,隧穿图像仍然适用[11],但在Keldysh 参数γ＞1 的情况下,隧穿图像是否成立,平面波近似是否成立,激发态对谐波椭偏率有什么影响? 为了回答上述问题,研究高频场中谐波的椭偏率问题成为必然.

通过数值求解二维含时Schrödinger 方程,研究了高频激光场中对称分子高次谐波的偏振特性;结果表明:分子谐波的偏振特性与激光强度、激光波长、核间距及取向角有关;利用数值方案,确定了在两中心干涉区,激发态在对称分子辐射的平行谐波谱中起重要作用,对于不同角度的垂直谐波,激发态的影响非常小,激发态对平行谐波和垂直谐波的不同影响导致精确垂直和精确平行谐波谱的强度比与仅跃迁回基态的垂直和平行谐波谱的强度比不同,且精确谐波谱与仅跃迁回基态的谐波谱的相位差不同,进而导致激发态对谐波椭偏率的影响具有强烈的角依赖性.此外,偏振的目的是对高频激光场中强场近似的检验,尤其是对平面波近似的检验.

2 理论方法

2.1 数值方法

其中ψ(t) 为与哈密顿H(t) 对应的含时波函数.基于强场近似理论,与基态再结合的电子对谐波辐射起主要贡献.因此有

(2)式表示电子从连续态返回至基态辐射的高次谐波,其中a0(t)=〈0| ψ(t)〉,式中未考虑激发态对高次谐波产生的贡献.此外,垂直谐波和平行谐波的振幅率及相位差决定了谐波的椭偏率[12]:

2.2 解析方法

基于强场近似,对于原子和对称分子,由于势的对称性,只辐射奇次谐波,其产生路径可简单地表示为〈p|ex·r|0〉i〈0|e·r|p〉r,意味着电子从相同的初始态 |0〉电离并与之复合,其中初始态 |0〉具有确定的宇称;在高次谐波产生中,偶极子矩阵元〈p|ex·r|0〉i为与电子沿激光极化方向ex的电离有

基于强场近似,谐波辐射谱由分子结构决定[2]:

式中,a(ω) 是连续态电子隧穿时的谱振幅,不随分子取向角而变化,且不依赖于连续态|p〉的能量,因此可得沿激光偏振方向的高次谐波谱S//(ω,θ) 与对应偶极矩D//(ω,θ) 之间的定性关系,进而可知隧穿图像成立.

3 计算结果和讨论

3.1 干涉效应

图1(a)、图1(b)和图1(c)分别表示由(3)式计算的分子在核间距R=1.7 a.u.,R=2 a.u. 和R=2.3 a.u. 及不同取向角下的谐波椭偏率曲线,随着核间距的变化,谐波最大椭偏率所处的谐波阶的位置会改变;图1 中第二、三行图是与谐波椭偏率曲线对应的角依赖的谐波谱和偶极子曲线,其与谐波椭偏率曲线趋势相反,在不同取向角下,图1(d)、图1(e)及图1(f)中谐波相对产量与图1(g)、图1(h)及图1(i)中相应偶极子曲线符合的很好,如(5)式所述,(5)式是基于隧穿图像得到的,该现象表示隧穿图像在高频激光场中成立,同时(5)式中偶极子的连续态|p〉由平面波函数近似得到,进而可得在高频激光场中平面波近似也成立.但是谐波谱和偶极子曲线之间存在显著的差异,图1(g)、图1(h)及图1(i)中的偶极子曲线展示了一个清晰的最小值,这个最小值起源于两中心干涉效应,但在图1(d)、图1(e)及图1(f)中对应的谐波谱曲线上未观察到该最小值,文献[27]中详细讨论了高频激光场中对称分子谐波谱上由两中心干涉效应而导致的最小值消失的原因,即在短波长(高频激光场)的情况下,由于激发态对分子高次谐波的重要贡献,导致干涉引起的凹槽在高次谐波谱中消失.通过对谐波椭偏率曲线及相应偶极子曲线的深入比较发现偶极子曲线上的最小值对应最大椭偏率所处的谐波阶位置,暗示了通过谐波椭偏率测量来探测高频激光场中对称分子偶极子上的最小值是可行的,因此在高频激光场中,两中心干涉效应是谐波椭偏率的起源.因为在θ=50°下偶极子曲线上未出现最小值,因此谐波在θ=50°基本不极化,即使在某些区域有极化,也是因为两中心干涉效应,谐波在θ=50°不极化这一现象说明在没有干涉效应的情况下(5)式依然是成立的,即在没有干涉效应的情况下,隧穿图像和平面波近似在高频激光场中都成立.

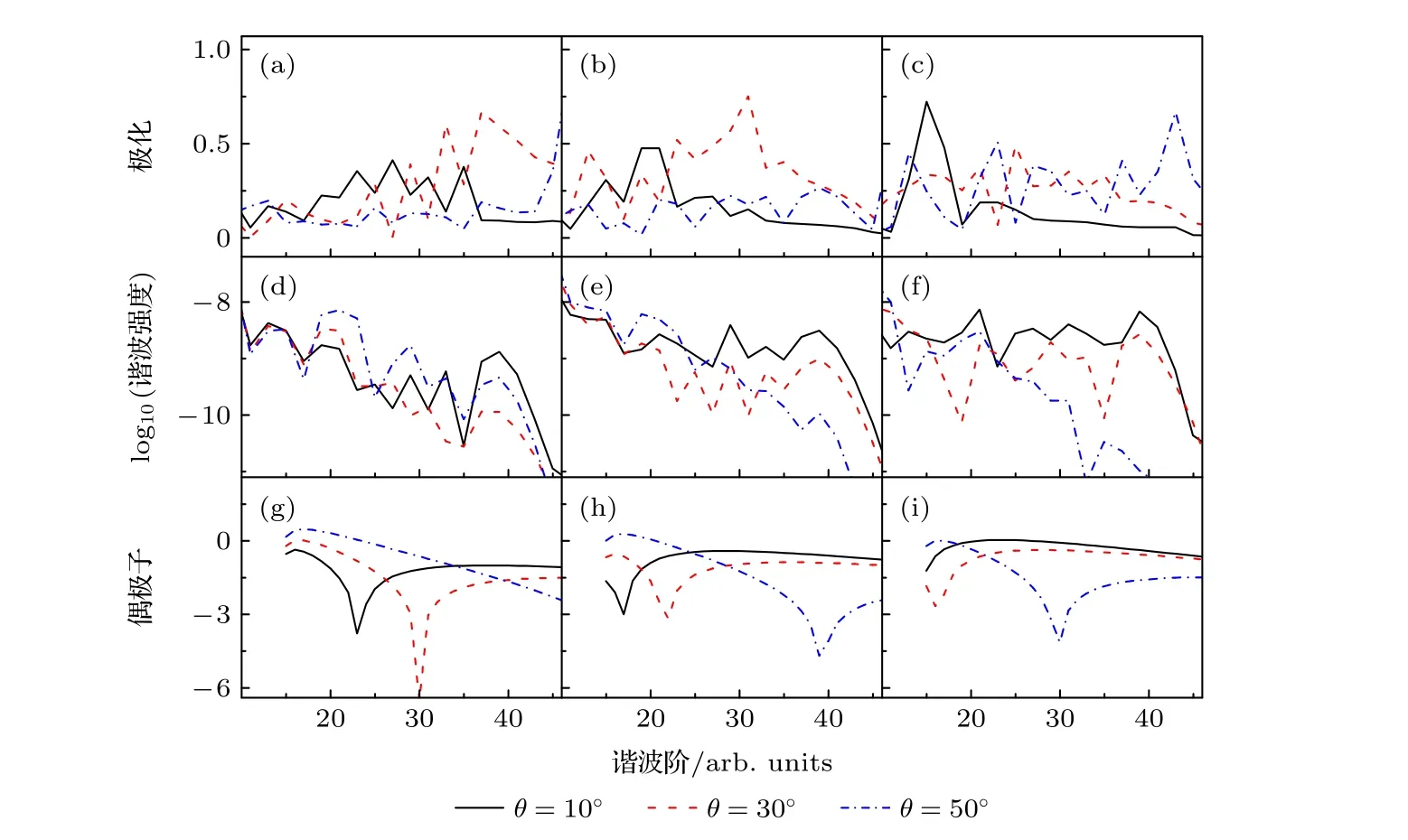
图1 分子在激光强度 I=4×1014 W/cm2 及波长 λ=600nm 时谐波的椭偏率、谐波谱及偶极子的比较 (a),(d),(g) 核间距为 R=1.7 a.u.;(b),(e),(h) 核间距为 R=2 a.u.;(c),(f),(i) 核间距为 R=2.3 a.u.Fig.1.Comparison of the harmonic ellipticity,harmonic spectra and corresponding dipole for molecules at the laser intensity I=4×1014 W/cm2 and wavelength λ=600 nm : (a),(d),(g) R=1.7 a.u. ;(b),(e),(h) R=2 a.u. ;(c),(f),(i) R=2.3 a.u..

与图1 类似,图2 和图3 给出了激光强度I=5×1014W/cm2、波长λ分 别为400 和500 nm 的谐波椭偏率曲线、谐波谱曲线和偶极子曲线.随着激光参数的变化,由(4)式计算的偶极子曲线上的最小值移向其他谐波阶,如图2 和图3 第三行所示.同时图2 和图3 中的谐波相对产量与相应偶极子曲线依旧一一对应,如(5)式所述,上述现象说明随着激光参数的改变,隧穿图像和平面波近似在高频激光场中成立,另外,由于图2(d)、图2(e)、图2(f)和图3(d)、图3(e)和图3(f)中谐波谱曲线上的最小值未出现,谐波的最大椭偏率仍旧对应偶极子曲线最小值所在的谐波阶,因此,两中心干涉效应为谐波最大椭偏率的起源.最重要的是随着激光参数和核间距的改变,谐波在θ=50°基本不极化,即使在某些区域有极化,也是因为两中心干涉效应,如图2 和图3所示.因此谐波在θ=50°不极化这一现象说明在没有干涉效应的情况下(5)式依然是成立的,因此椭偏率测量至少在本文计算的Keldysh参数范围内(1 .028 ≤γ≤1.377)给出了(5)式的适用性.

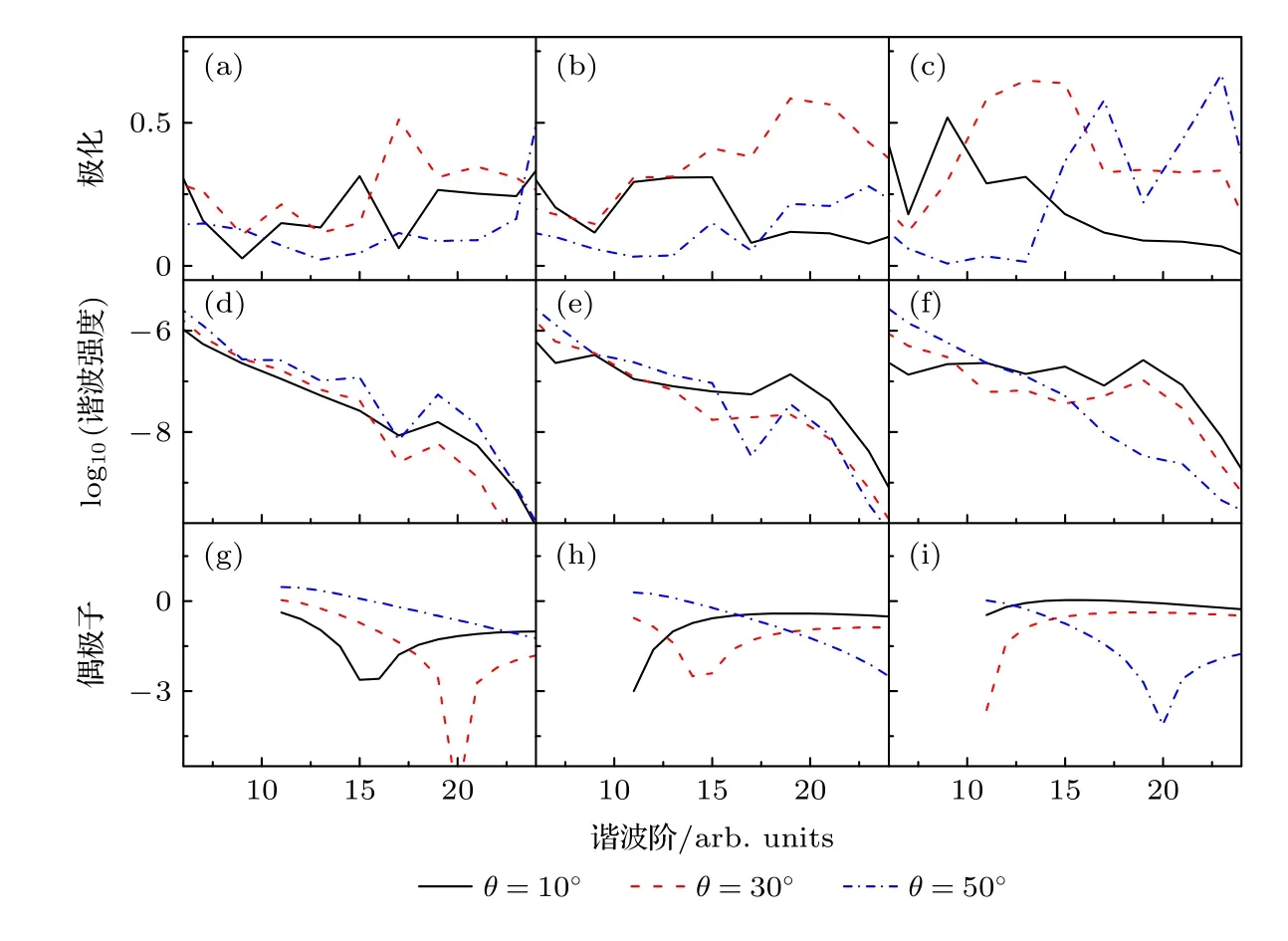
图2 与图1 相同,但激光强度 I=5×1014 W/cm2 和波长 λ=400 nmFig.2.Same as Fig.1,but the laser intensity I=5×1014 W/cm2 and wavelength λ=400 nm.

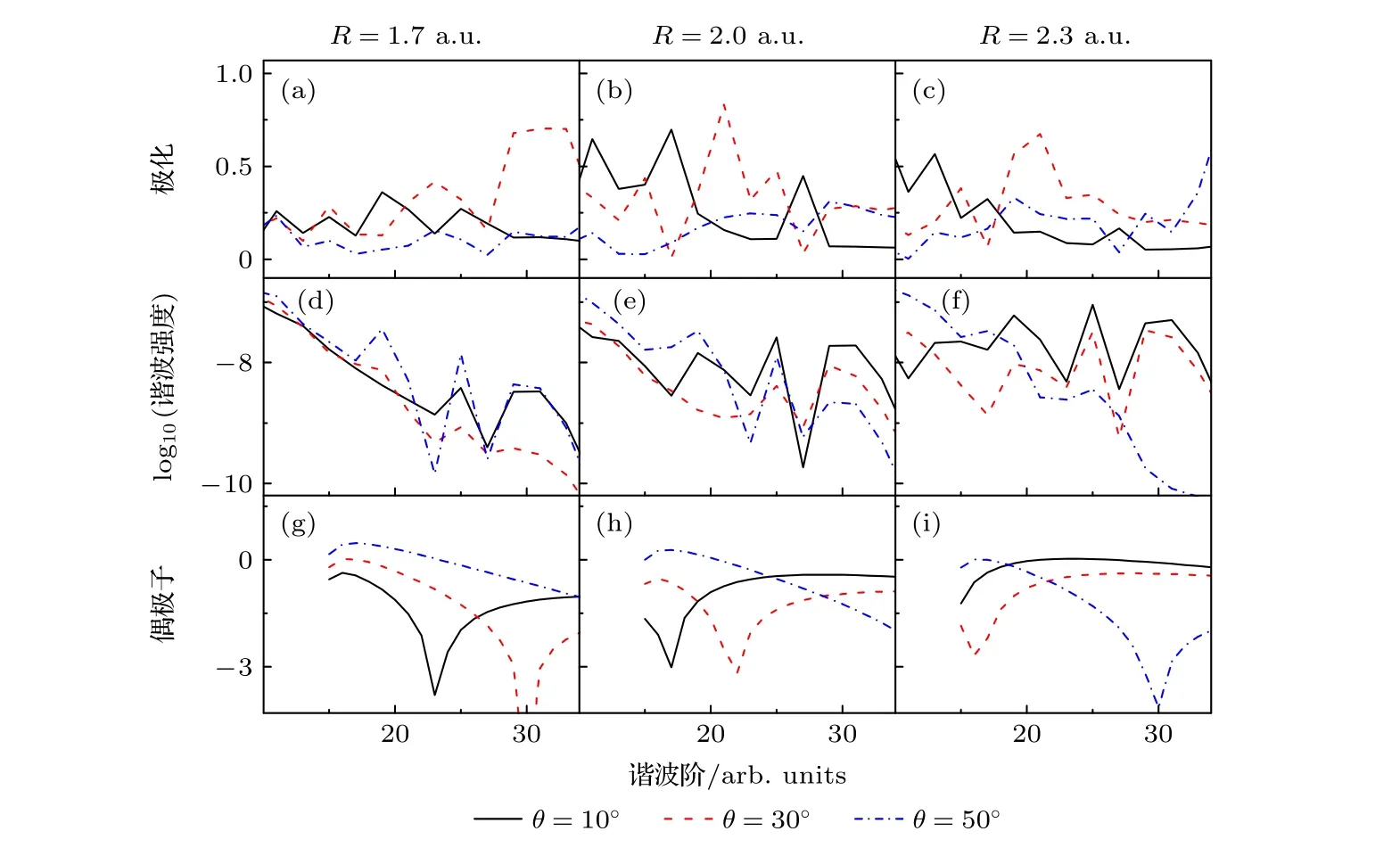
图3 与图1 相同,但激光强度 I=5×1014 W/cm2 和波长 λ=500 nmFig.3.Same as Fig.1,but the laser intensity I=5×1014 W/cm2 and wavelength λ=500 nm.

3.2 激发态效应

由于激发态对分子高次谐波的重要贡献,导致干涉效应引起的凹槽在高次谐波谱中消失,那么激发态是如何影响谐波椭偏率的? 因此在图4 中,研究了激发态对谐波椭偏率特性的影响,将(1)式计算的结果(实线)与(2)式计算的结果(短虚线)进行比较,其中(1)式包含所有束缚态对高次谐波的贡献(精确谐波),(2)式只考虑电子返回到基态对高次谐波的贡献(基态谐波);对于图4(a)中θ=10°的小角及图4(b)中θ=30°的中间角情况,只跃迁至基态的谐波谱显示一个大的抑制区域,其在精确谐波谱中消失.另外,图4(a)和图4(b)中基态谐波(短虚线)上的抑制区域对应于图4(g)和图4(h)中偶极子曲线上的凹槽,如虚线箭头所示,该偶极子曲线由(4)式计算得到;结果表明,激发态在干涉诱导凹槽区影响高次谐波的产生;然而,在不同取向角下,激发态对谐波椭偏率的影响是不同的,如图4(d)—(f)所示;例如,对于图4(d)中θ=10°的情况,基态谐波的椭偏率(短虚线)显示了一个尖锐的峰值,该曲线由(2)式代入(3)式计算得到,而精确谐波椭偏率(实曲线)峰值显示了更广泛的分布,该实曲线由(1)式代入(3)式计算得到;图4(e)中θ=30°的中间角情况则相反,由(2)式计算的跃迁回基态的谐波谱在此角度上的椭偏率很小(短虚线),而由(1)式计算的精确谐波(实曲线)具有显著的椭偏率.对于θ=50°的大角情况,在两中心干涉区,由(2)式计算的基态谐波谱略偏离由(1)式计算的精确谐波谱,如图4(c)所示;然而,当图4(f)中的实曲线显示小的椭偏率时,图4(f)中的短虚线则显示大的椭偏率.

图4 分子 I=4×1014 W/cm2,λ=600 nm 及R=2 a.u.时谐波谱、偶极子和谐波椭偏率的比较 (a),(d),(g) θ=10° ;(b),(e),(h) θ=30° ;(c),(f),(i) θ=50°Fig.4.Comparison of the harmonic ellipticity,harmonic spectra and corresponding dipole for molecules with R=2 a.u.at the laser intensity I=4×1014 W/cm2 and wavelength λ=600 nm : (a),(d),(g) θ=10° ;(b),(e),(h) θ=30° ;(c),(f),(i) θ=50°.

下面,探讨了激发态对谐波椭偏率影响的起源.对于图5 中θ=10°的情况,其具有与图4 相同的激光和分子参数;在图5(a)中,在由(2)式计算的基态谐波谱(短虚线)上可观察到大的抑制区域,该区域在由(1)式计算的精确谐波谱(实曲线)中消失;然而对于图5(c)中垂直谐波情况,由(2)式计算的基态谐波谱(短虚线)与由(1)式计算的精确谐波谱(实曲线)非常相似;上述现象表明,激发态对平行和垂直谐波的影响不同,导致精确谐波的相位差较大,如图5(e)所示.然而,当分别比较图5(b)中由(1)式计算的平行和垂直谐波谱和图5(d)中由(2)式计算的平行和垂直谐波谱时,发现在图5(b)的整个谐波平台区域,精确垂直谐波的相对产量低于精确平行谐波的;在此情况下,在两中心干涉区,由于消除了激发态对高次谐波的贡献,由(2)式计算的基态垂直谐波的相对产量与基态平行谐波的相当,如图5(d)所示;因此,在两中心干涉区,由(1)式计算的精确垂直谐波和精确平行谐波之间小的强度比归因于激发态对谐波的贡献,该影响导致图5(f)中精确谐波谱显示小的椭偏率.换言之,即使精确谐波的相位差大于基态谐波的相位差,但由(1)式获得的垂直和平行谐波之间的强度比非常小,导致图5(f)中精确谐波频谱显示出小的椭偏率,在这种情况下,激发态抑制了谐波的椭偏率.

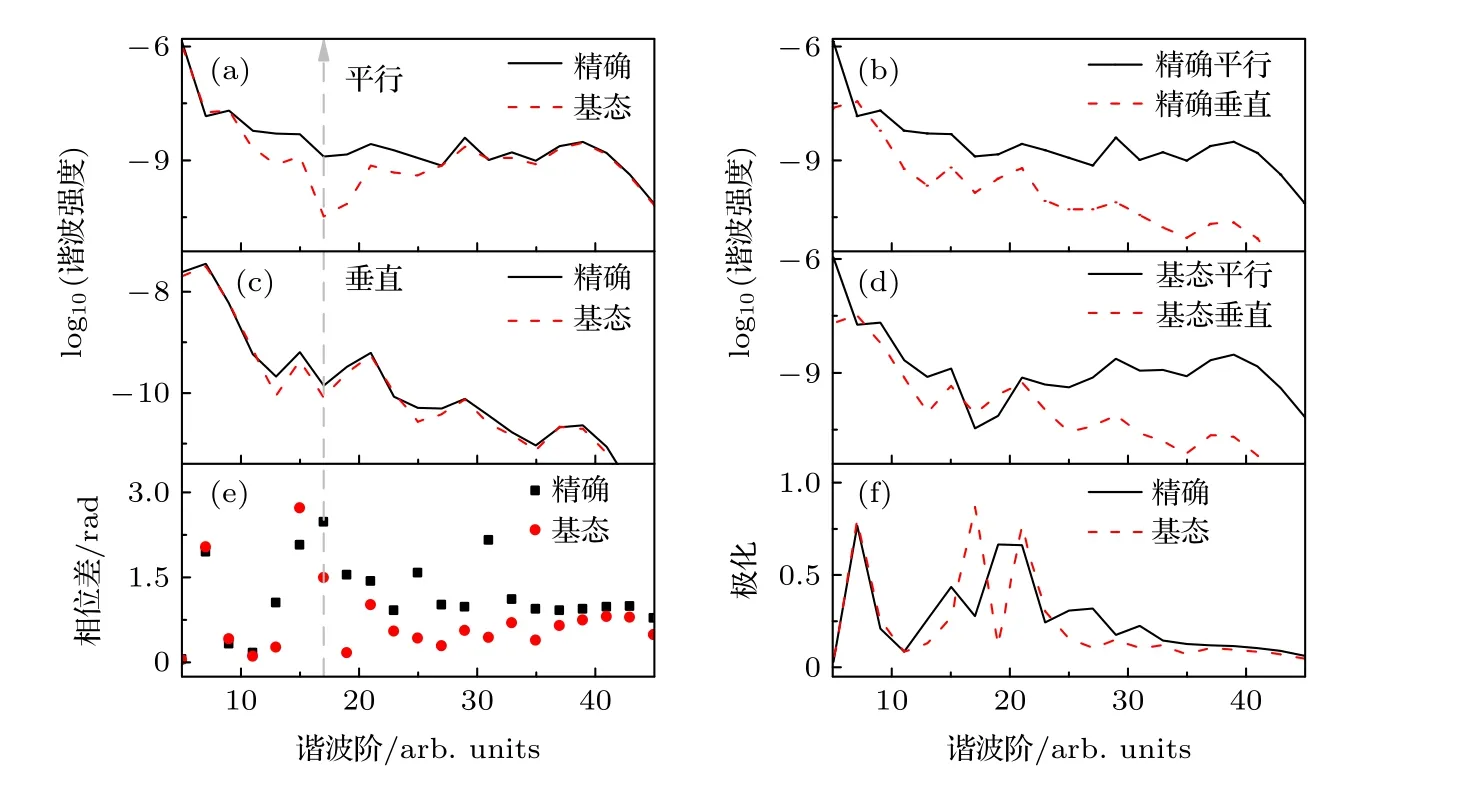
图5 分子 I=4×1014 W/cm2,λ=600 nm,R=2 a.u.及 θ=10° 时谐波谱、相位差和谐波椭偏率的比较 (a) 精确平行与跃迁回基态的平行谐波谱(基态平行谐波)比较;(b) 精确平行与精确垂直谐波谱的比较;(c) 精确与基态垂直谐波谱的比较;(d) 基态平行与基态垂直谐波谱的比较;(e) 精确与基态谐波相位差比较;(f) 精确与基态谐波椭偏率比较Fig.5.The comparison of the harmonic spectra,the phase differences δ1(d) and the ellipticity of harmonic for molecules with R=2 a.u.and θ=10° at the laser intensity I=4×1014 W/cm2 and wavelength λ=600 nm : (a) The comparison of accurate parallel harmonic and the parallel harmonic that transition back to ground state (ground-state parallel harmonic);(b) the comparison of accurate parallel and perpendicular harmonic;(c) comparison between accurate and ground state perpendicular harmonic spectrum;(d) comparison between ground-state parallel and ground-state perpendicular harmonic;(e) the comparison of the phase difference of accurate and ground-state harmonic;(f) comparison between accurate and ground-state harmonic ellipticity.

对于图6 中θ=30°的中间角,在平台区域,激发态对平行和垂直高次谐波的影响与图5 类似,即激发态对平行和垂直谐波的贡献不同,导致精确谐波产生较大的相位差.此外,在图6(b)的两中心干涉区,由(1)式计算的精确垂直谐波强度与精确平行谐波强度相当,由于图5(b)中精确垂直谐波与精确平行谐波的强度比小,因此θ=10°时图5(f)中精确谐波的椭偏率低于θ=30°时图6(f)中精确谐波的椭偏率,这些数值分析揭示了为什么图1(a)中θ=10°的谐波椭偏率峰值低于图1(a)中θ=30°的谐波椭偏率峰值.且由于激发态的缺失,由(2)式计算的图6(a)中基态谐波谱(短虚线)出现了一个较宽的抑制区域,进而使得该区域基态平行谐波的相对产量偏离基态垂直谐波的相对产量,如图6(d)所示.这些影响表明,由(1)式计算的精确垂直谐波和精确平行谐波之间大的强度比归因于激发态对谐波的贡献,因此由(1)式计算的精确谐波谱显示高的椭偏率,如图6(f)所示;激发态增强了谐波的椭偏率.

图6 与图5 相同,但 θ=30°Fig.6.Same as Fig.5,but θ=30°.

应当指出,对于图7 中θ=50°的情况,激发态在两中心干涉区对平行谐波具有较小的影响,如图7(a)所示;在整个平台区域,激发态不影响垂直谐波,见图7(c),该结果导致在两中心干涉区,由(2)式计算的图7(d)中垂直和平行谐波之间的强度比大于由(1)式计算的图7(b)中垂直和平行谐波的强度比,且使得精确谱的相位差δ1∼0.16π ;相应的在两中心干涉区,由(1)式计算的谐波谱具有低椭偏率,因此,激发态抑制了谐波的椭偏率.

为使研究更全面,在不同取向角及其他激光参数下,例如取向角θ=20°,θ=40°,θ=60°,激光强度I=5×1014W/cm2及波长λ=400 nm,λ=500 nm,检验了谐波椭偏率的行为,上述观察到的现象基本不变,即在两中心干涉区,激发态对平行谐波有重要影响,但垂直谐波不受激发态影响,进而导致精确谐波和基态谐波相位差不同;且在不同取向角,激发态对谐波椭偏率的影响是不同的.总的来说,虽然由(1)式计算的精确垂直谐波的相对产量低于(高于)精确平行谐波的,但在两中心干涉区,由于激发态的缺失,由(2)式计算的基态垂直谐波的强度更接近(远离)基态平行谐波的强度.相应的,由(1)式计算的精确垂直谐波和精确平行谐波之间小(大)的强度比归因于激发态对谐波的贡献.因此,可得出结论,而由(1)式代入(3)式计算的精确谐波椭偏率具有低(高)的椭偏率,激发态抑制(增强)了谐波的椭偏率,大角度谐波椭偏率的起源与图7(f)中的曲线相似.

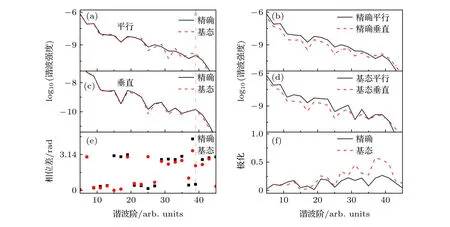
图7 与图5 相同,但 θ=50°Fig.7.Same as Fig.5,but θ=50°.

需要强调的是在上述讨论中,我们没有考虑较大核间距的情况.对于高频激光场的情况,由于激光频率较高,核间距较大分子的基态和激发态之间的耦合可能会对谐波辐射产生重要的影响.此时只考虑基态贡献的强场近似模型不适用,需要在通常的强场近似模型中引入激发态贡献[36]例如R=4 a.u.,此时基态和激发态强耦合,其贡献可比.关于高频场中核间距大的分子谐波椭偏率的研究,将在未来的工作中做进一步的详细研究.

4 总结