水声射线传播的黎曼几何建模·应用——深海远程声传播会聚区黎曼几何模型*

马树青 郭肖晋 张理论 蓝强 黄创霞

1) (国防科技大学气象海洋学院,长沙 410073)

2) (长沙理工大学数学与统计学院,长沙 410114)

会聚区是深海水声传播重要的物理现象,对其准确建模和计算是深海远程水声探测与通信的基础.但深海会聚区缺乏明确的数学描述,特别是对于地球曲率所导致的系统误差,目前主要采用近似计算与曲率修正相结合的方法,尚无精确会聚区数学模型.本文基于水声射线黎曼几何建模基础理论研究,在弯曲球体流形上开展深海会聚区建模,在分析总结会聚区物理特征的基础上,给出深海会聚区黎曼几何描述,得到深海会聚区位置、距离的分析形式和基于黎曼几何概念的计算方法,为深海会聚区—这一重要的深海声学现象探索赋予黎曼几何学意义.以Munk 声速剖面为例,对比分析深海会聚区在曲率修正和采用黎曼几何方法在球体流形上建模两种情形的时空分布,验证了本文提出的深海会聚区黎曼几何模型的有效性,结果显示近海面处的会聚区宽度随声传播呈现先变大后变小的规律,最大约20 km,最小约4 km.

1 引言

深海典型声速分布使声线在远离声道轴处上下反转或反射,形成周期性高声强焦散区域,称为会聚区[1].会聚区内声信号的传播损失小,能够高强度、低失真地远距离传播声信号.准确预测和识别会聚区是深海声学研究的重要课题.前人围绕深海会聚区的观测、影响因素和分析建模等开展了大量深入细致的工作,然而基于射线方法的会聚区声场数学描述还不完善,束缚了对会聚区的有效利用.

声传播实验观测是会聚区研究的基础.1960 年,Hale[2]在实验数据基础上首次分析了海面附近会聚区的物理特征,指出一定范围内,会聚区声信号比其他路径高出约30 dB,其边界为焦散线.Urick[3]基于实验数据和声线图,研究声源和接收深度对会聚区的影响,发现会聚区通常存在于整个深海声道,声源变深时会聚区分裂成两个半区,且间距逐渐增大.朴胜春等[4]结合南海海域的远程声传播实验结果,发现深海大深度处存在着下反转点会聚区,其位置与焦散线吻合.李文和李整林[5]利用南海爆炸声信号分析海底山对会聚区声传播的影响,发现海底山阻挡可使第一会聚区处的传播损失增加30 dB 以上.

建模与预测是会聚区研究的重点,其中会聚区距离和宽度是关键模型要素.由于0°掠射角声线反转点附近存在焦散线[6],一系列学者[7-10]将会聚区距离定义为0°掠射角声线反转点的循环距离.文献[5,11]则将声源深度处传播损失曲线的峰值作为会聚区,将其差值作为会聚区距离.张晶晶和罗博[12]通过计算两条邻近声线的交汇点估计会聚区的峰值.Yang 等[13]基于卷积神经网络(CNN)模型提出了一种会聚区的判别方法.张仁和[7]利用简正波和广义射线理论[6]研究了反转点会聚区的声场,指出发射深度的反转点附近通常存在着3 条焦散线,认为会聚区在0°掠射角声线的上反转点附近形成.庄益夫等[11]利用Bellhop 高斯声束模型分析了深海声速剖面结构变化引起的会聚区偏移特征,发现混合层、主跃层、深海等温层及声道轴变化均会导致会聚区位置偏移.Wu 等[10]利用抛物方程研究声速剖面对会聚区位置的影响,分析了南海、东印度洋的区域差异.以上研究主要通过观察声线图或传播损失曲线的变化定性地分析会聚区的宽度.可见深海会聚区数学描述还不明确,缺乏关于会聚区位置、距离和宽度的精确计算方法.另一方面,会聚区模型预测与声学实验观测间仍存在明显的差异.南海某爆炸声传播实验[14]结果显示,会聚区的实验观测位置相比理论计算的反转点位置有所前移,第一会聚区约前移1—3 km,第二会聚区前移超过10 km.Vadov[15]指出第一会聚区的模型预测理论位置通常比实验观测结果高出了1—2 km.

同时,会聚区建模需要充分考虑地球曲率对远程声传播的影响.徐传秀等[16]对抛物模型进行地球曲率修正,结果表明,地球曲率会造成会聚区向远距离移动.毕思昭和彭朝晖[17]给出了基于共形映射的地球曲率修正方法,结果显示地球曲率会导致会聚区位置向声源方向偏移.Munk 等[18]根据费马原理给出了大地坐标系下的声学射线方程,在其基础上,Yan 和Kang[19]与Yan[20]建立了考虑地球曲率影响的二维和三维射线方程,发现射线路径向声源方向移动,但未研究会聚区.考虑到球面和平面间有共形映射,但不存在等距映射,因而采用“欧氏空间建模+曲率补偿”的方法,在本质上是不完备的,势必需要在弯曲流形上直接建模才能得到精确模型.

综上,分析会聚区数学物理机理、研究考虑地球曲率的会聚区精确模型具有重要学术与应用意义.文献[21]研究建立了水声射线黎曼几何模型,分析了水声场射线的几何拓扑性质,发现声线会聚导致焦散现象的根本数学意义是: 流形上的正截面曲率导致测地线形成共轭点.在以上工作的基础上,运用黎曼几何中截面曲率、雅可比场和共轭点等概念,从黎曼几何视角给出会聚区的数学描述,针对考虑地球曲率的远程声传播情形,建立了深海会聚区黎曼几何模型,发现考虑地球曲率后截面曲率增加了一项(l)(l)/l,体现了地球曲率对声场射线拓扑结构以及会聚区的影响.以Munk 声速剖面为例,给出了深海会聚区远程时空分布.结果显示,相比不考虑地球曲率情形,会聚区在远程传播时向声源方向移动,第16 个上反转点会聚区(传播距离约为932 km)约前移9.6 km.同时发现近海面的会聚区宽度随声传播呈现先变大后变小的现象,最大约20 km,最小约4 km.

本文给出的考虑地球曲率的深海会聚区黎曼几何数学形式,使会聚区远程声传播研究开始具备现代黎曼几何意义.论文安排如下: 第2 节给出地球球体流形上自然考虑地球曲率的黎曼几何声传播模型;第3 节分析研究会聚区物理特征,在测地线、雅可比场、共轭点等几何概念基础上,给出深海会聚区黎曼几何描述;第4 节以Munk 声速剖面为例,分析对比了会聚区黎曼几何数学模型的有效性;第5 节为全文总结和展望.

2 球体流形上的远程声传播建模

地球近似为一个球体,地球曲率会造成水声波导弯曲,因此对水声学中常见的水平分层声传播场景而言,实际海洋声传播的声速等值面是同心球面,而非平行平面,因而远程声传播必须考虑地球曲率.基于文献[21]的黎曼几何射线建模理论基础,给出考虑地球曲率的深海远程声传播射线模型.

2.1 水声射线走时的几何描述

设 (l,θ,φ) 是以地球球心为原点的球坐标系,R=6370.856 km 是地球的曲率半径,假设为常数,海水深度为Hm,海面边界为la=R,海底边界为lb=R-H.声源在l轴上(θ=0,φ=0),且位于海面和海底之间.考虑地球曲率后,海洋波导是一个三维球面环体流形:

欧氏度规下的线元 ds2=dl2+l2dθ2+l2sin2θdφ2,弧长s的黎曼度规为

gij与互称为共形度规.(1)式和(2)式分别表示两种不同的流形结构,(1)式为三维欧氏度规的球坐标表示,(2)式为水声射线传播的时空流形结构.

设单个点源是全向的,且声线不随方位角变化发生扭转,此时方位角恒定的截面的声传播是对称的,见图1.问题转化到二维 (l,θ) 平面上,即二维微分流形N={(l,θ)|la ＜l ＜lb,θ ∈(0,π)}.此时传播距离=lθ,深度=R-l.传播时 间t的 度规σ ∈[a,b] 是流形 (N,) 上的曲线,σ为线参数,黑体表示向量,沿着曲线x(σ) 的走时T为

图1 考虑地球曲率后的声传播 (a) 对称截面;(b) (l,θ) 平面上的雅可比场几何示意图Fig.1.Sound propagation considering the earth curvature: (a) Symmetrical section;(b) geometric structure of Jacobi field.

2.2 水声测地线程函方程

在传播时间t的度规下,声线是沿着测地线传播的.自然参数t下黎曼流形 () 的测地线方程为

设α0是初始掠射角,则射线方程(6)的初值条件为

初值问题(6)式和(7)式刻画了黎曼流形 (N,) 上的水声射线程函方程.

2.3 声线几何扩展的雅可比场描述

测地线的雅可比场刻画了声线的内蕴几何扩展,雅可比方程给出了内蕴几何扩展的求解方法(图1(b)).记x(t,α) 是二维黎曼流形 (N,) 上从声源处发出的以时间t为参数的声线(测地线),α为掠射角,映射f(t,α)=x(t,α).由文献[21]可知,

是变分f沿声线x(t,α0) 的雅可比场.记x(t)=x(t,α0),取单位正交标架场:

雅可比场Y1(t) 表示声线的内蕴几何扩展,满足雅可比方程:

其中K(e1,e2) 表示截面曲率,反映了流形的几何拓扑结构.根据

结合(5)式,有

截面曲率K(u,v) 与二维截面 [u ∧v] 的基底u,v的选取无关,因此

结合(8)式和(10)式,可以得到雅可比方程:

若雅可比场Y1(tk)=0,则x(tk) 为黎曼流形中的共轭点,即水声学中的焦散点.此时声线x(t) 周围的声线在x(tk) 附近会聚.

声线的几何扩展决定了射线束的横截面积S,设q为外蕴几何扩展,α0是初始掠射角,对于径向对称的点源声场[1]:

设W为单位立体角内的辐射声功率,由射线管内能量守恒性质,单根声线声强的基本公式为

沿着一个射线束的几何扩展损失定义为某一点的声强I(l,θ) 与距离声源1 m 处的声强I0之比[1],单位为分贝(dB),即

为了便于理解,上述推导给出了利用文献[21]建模方法推导球面分层介质的完整过程.事实上,考虑到黎曼度规、截面曲率和测地线方程均为流形的内蕴形式,不随坐标系改变而变化,故可由文献[21]的(21)式、(29)式和(33)式直接得到球面分层介质的测地线程函方程(6)和雅可比方程(11)(细节不再赘述).

2.4 地球曲率的黎曼几何效应分析

根据文献[21]中的(29)式和(34)式可知,当不考虑地球曲率影响时,水平分层介质中二维测地线(射线)方程为

这里r和z是柱坐标系下的传播距离和深度,初值条件为

截面曲率:

雅可比方程:

沿着一个射线束的几何扩展损失为

由(8)式可知,截面曲率决定了雅可比场Y1(t)的计算结果.比较截面曲率(10)和(17)式,可以发现在相同深度处考虑地球曲率影响前后的截面曲率相差(l)(l)/l,这将影响水声射线的几何扩展速率及声场射线拓扑结构.对于深海水下声道型声速剖面,在声道轴以上,(l)(l)/l ＞0,考虑地球曲率后截面曲率增大;在声道轴以下,(l)(l)/l ＜0,此时考虑地球曲率后截面曲率减小.下文仿真将给出对雅可比场及会聚区的相关数值影响效应.

3 深海会聚区黎曼几何建模

本节利用截面曲率、雅可比场和共轭点等几何概念,结合会聚区的物理特征,给出会聚区的数学描述与计算方法.在经典的水声学教材[1,23]中,会聚区被定义为从近海面声源发出的波束经过深海折射路径传播后,重新在近海面附近会聚,形成的周期性高声强焦散区域.Hale[2]指出在较长的范围内,会聚区的声信号比其他路径传播的声信号高出约30 dB,且会聚区的边界不是底部掠射声线,而是声线会聚形成的焦散线.张仁和[6,7]证明了发射深度的反转点附近通常存在着3 条焦散线,认为会聚区在0°掠射角声线的上反转点附近形成,将0°掠射角声线上反转点的距离作为会聚区距离.最近,一些研究[4,17]发现在深海大深度处折射型声线的焦散线附近也存在着与海面附近类似的周期性高声强区域,称为下反转点会聚区.由于对会聚区产生主要影响的是折射型声线[12],在本文中暂不考虑边界影响,仅考虑折射型声线产生的会聚区效应.

基于上述研究分析,总结会聚区的3 个基本物理特征如下:

1) 会聚区的边界是焦散线,0°掠射角声线的上反转点附近通常存在着三条焦散线;

2) 会聚区的深度位于近海面(上反转点)或深海大深度(下反转点)处,距离具有周期性;

3) 会聚区处产生了声线会聚现象,因此具有较高的声强.

声线会聚产生的焦散现象在黎曼几何中表现为测地线的雅可比场为0,即出现了共轭点.根据雅可比方程(8)式可知,截面曲率完全决定了雅可比方程的解.共轭点的形成与流形上的截面曲率有关.共轭点定理[21,24]表明,如果流形上的截面曲率均小于或等于零,则不会产生共轭点.如果流形上的截面曲率有正的下界,那么所有完备的声线均会产生共轭点.从(10)式可以看出,截面曲率K的值取决于声速剖面和海洋深度.流形上截面曲率的变化揭示了水声场射线的几何拓扑结构,反映了海洋环境变化对水声场的影响.若声线始终在 0＜Kinf≤K≤Ksup的介质中传播,那么声线终将产生焦散点,且相邻焦散点的时间间隔.若声线穿过K＜0 的介质区域,那么声线可能会变得不稳定.因此,产生焦散现象的必要条件是水声场存在正截面曲率.

结合会聚区物理性质和焦散点几何性质的研究,本文利用黎曼几何方法,给出如下会聚区数学描述,用于会聚区建模计算:

1) 存在截面曲率K＞0 的稳定区域,且通过求解测地线方程(6)和Jaocbi 方程(11),声线出现了共轭点;

2) 在深海上下反转区域内存在共轭点集合,且具有准周期现象;

3) 当上反转区域内声束的几何扩展损失(14)式小于阈值β时,则出现了上反转点会聚区,定义为

4) 与文献[7]的理论结果一致,本文仿真结果显示0°掠射角声线的上下反转点附近存在3 条焦散线.因此,本文将0°掠射角声线的反转点作为会聚区的参考点,会聚区距离定义为0°掠射角声线反转点的距离.记 C Zk为第k个会聚区,深度0处第k个会聚区的宽度为

由(14)式和(20)式可知 (,)∈CZk需满足以下条件:

下文数值仿真验证了由黎曼几何建模计算得到的会聚区满足上述深海会聚区的3 个物理特征.

4 深海会聚区黎曼几何模型的数值实验与分析

本节以Munk 声速剖面

为例,分别对考虑地球曲率影响((6)式,(10)式,(11)式,(14)式)和不考虑地球曲率影响((15)式—(19)式)时建立的深海会聚区几何模型进行仿真,并对仿真结果进行对比分析.

4.1 考虑地球曲率前后声场射线的几何性质对比

根据截面曲率(10)式和(17)式,可以看出Munk声速剖面(22)式下的截面曲率K不恒为常数,不能直接求出雅可比方程的解析解.在声道轴以上(1300 m),(l)(l)/l＞0,考虑地球曲率后截面曲率增大;在声道轴以下(1300 m),(l)(l)/l＜0,考虑地球曲率后截面曲率减小.这使得Munk 声速剖面下截面曲率的临界值发生了变化,见表1.

表1 考虑地球曲率前后Munk 声速剖面下截面曲率对比Table 1.Comparison of sectional curvature of Munk sound speed profile.

根据共轭点定理[21,24],如果声线始终在截面曲率K=0 时深度的临界值上方传播,那么声线一定会产生焦散点.若声线始终在截面曲率临界值的下方传播,那么声线将不断发散.截面曲率临界值的改变可能使原本稳定的声线变得不稳定,从而影响会聚区的形成.此外,根据截面曲率的最大值Kmax可知,不考虑地球曲率影响时相邻焦散点之间的时间间隔t≥5.8567 s,考虑地球曲率影响后相邻焦散点之间的时间间隔t≥5.8564 s.

选取50 根中心声线,利用四阶Runge-Kutta法计算考虑地球曲率与不考虑地球曲率的测地线方程(6)和方程(15),雅可比方程(11)和方程(18)的数值解,其中参数设置为H=5000 m,入射角α0∈[-8°,8°],频率ω=50 HZ,声源位于r(0)=0 m,z(0)=200 m,时 间t∈[0,a],a=660 s,此时所选声线均为折射型声线.中心声线上各点处的截面曲率和雅可比场的分量Y1(t) 的求解结果见图2 和图3.分析图2(a)可知,考虑地球曲率前后绝大多数声线均在截面曲率K＞0 的稳定区域中传播,少数声线穿过了K＜0 的不稳定区域,且所经过的不稳定区域的截面曲率接近于0.此外,比较同一初始条件出发的声线的截面曲率(图2(b)),数值结果显示在形成第一个焦散点之前,同一时刻考虑地球曲率后声线的截面曲率大于不考虑地球曲率的截面曲率.Rauch 比较定理是黎曼几何中的重要工具,刻画了不同流形上截面曲率对雅可比场的影响.

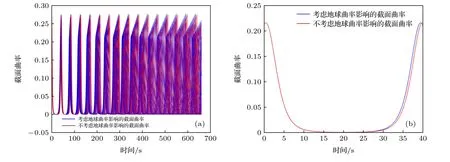
图2 考虑地球曲率前后所选声线的截面曲率 (a) 660 s 内50 根声线的截面曲率;(b) 入射角 α0=0° 的声线形成第一个焦散点前的截面曲率Fig.2.Section curvature before and after considering the earth curvature: (a) Section curvature of 50 sound lines in 660 s;(b) section curvature of sound line with elevation angle α0=0° before forming the first caustic.

根据Rauch 比较定理,在形成第一个焦散点之前,考虑地球曲率的雅可比场小于不考虑地球曲率的雅可比场,故先形成第一个上反转点会聚区.

雅可比场Y1(t) 的零点即焦散点的位置,从图3可以看出,考虑地球曲率前后均会不断形成焦散点,660 s 每根声线的焦散点个数为28—34 个.尽管少数声线穿过了K＜0 的不稳定区域,但经过的区域较小,且截面曲率接近于0,声线的发散速率不大,故所有声线均产生了焦散点,且形成焦散点的时间间隔符合上文分析.同时,随着声线的传播,雅可比场的极大值不断增大,说明声线束的几何扩展损失增大,声场能量损耗增大.

图3 660 s 内所选50 根声线的雅可比场 Y1(t)Fig.3.Jacobi field Y1(t) of 50 sound lines in 660 s.

4.2 地球曲率对深海会聚区位置和宽度的影响效应

利用几何扩展损失的计算公式(14)式和(19)式可得,不考虑地球曲率时几何扩展损失的最大值为113.3 dB,考虑地球曲率后几何扩展损失的最大值为113.8 dB.根据第3 节提出的深海会聚区几何模型,得到远程传播弯曲声道中(二维情形)的声线轨迹、焦散点以及会聚区位置,如图4.

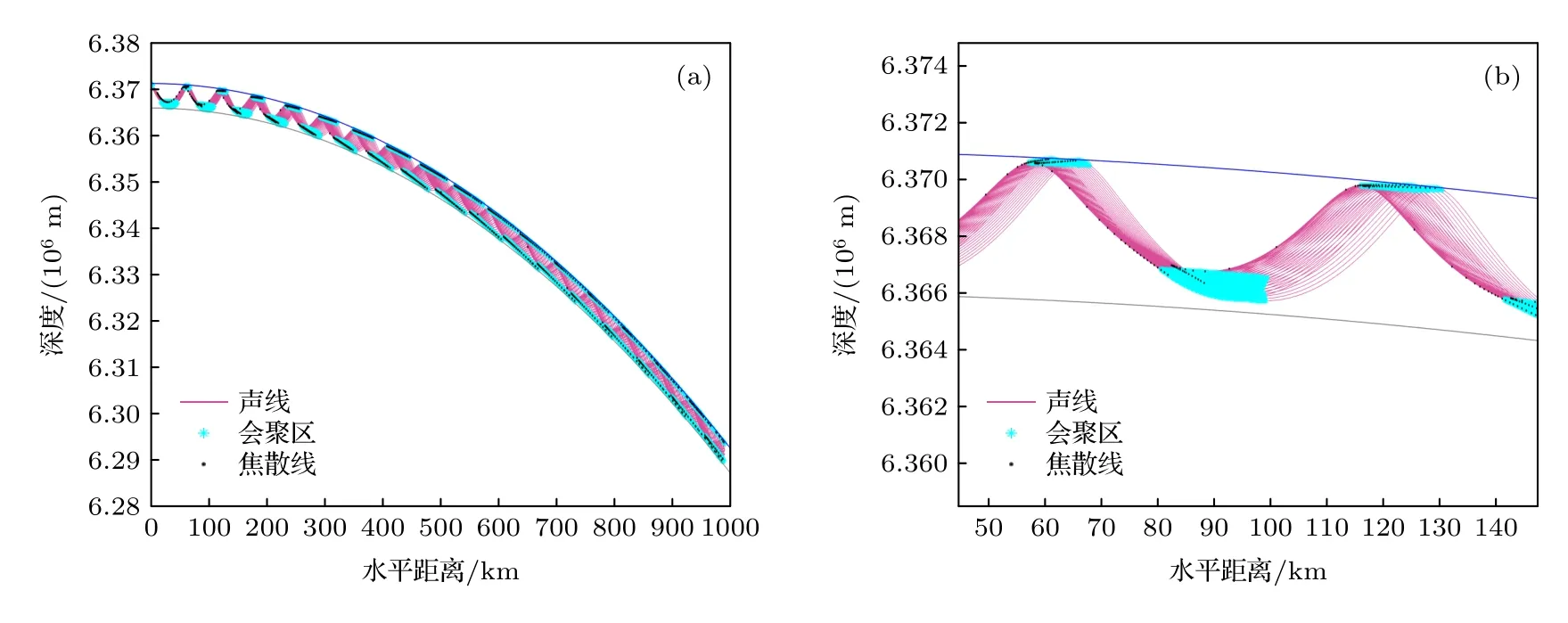
图4 弯曲声道中的声线、会聚区和焦散点 (a) 全图;(b) 细节图Fig.4.Ray,convergence zone and caustics in curved sound channel: (a) Full picture;(b) details picture.

从图4 可以看出,焦散点主要集中在声线的上反转点和下反转点位置,这说明在近海面处和深海大深度处均会产生明显的会聚区效应,且会聚区的边界存在焦散线,符合会聚区的物理特征,说明本文给出的会聚区计算方法是合理的.

为了便于分析地球曲率的影响,本文在深度-距离坐标系中计算了考虑地球曲率前后声线、焦散线和会聚区的位置(所选参数不变),见图5 和图6.从图5 和图6 可以看出,考虑地球曲率前后近海面和深海大深度处都出现了明显的焦散现象,0°掠射角声线的反转点附近出现了3 条焦散线(图5),这与前文的理论分析吻合.因此,考虑地球曲率前后在近海面(30—200 m)和深海大深度处(考虑地球曲率前约为3700—4610 m,考虑地球曲率后约为3660—4560 m)均存在明显的会聚区效应,1000 km距离内产生了16 个会聚区(图6).

图5 考虑地球曲率前后的声线和焦散线 (a) 全图;(b) 上反转点焦散线;(c) 下反转点焦散线Fig.5.Rays and caustics before and after considering the earth curvature: (a) Full picture;(b) upper turning point caustics;(c) lower turning point caustics.

图6 考虑地球曲率前后的声线和会聚区Fig.6.Rays and convergence zones before and after considering the earth curvature.

从图5 和图6 可以看出,考虑地球曲率后声线整体向声源方向移动,焦散点和会聚区也随之移动.仍以0°声线反转点作为会聚区位置的参考点,发现上、下反转点会聚区的传播距离均有所减小.随着传播距离的增大,会聚区前移距离近似线性增长(图7).

图7 考虑地球曲率后会聚区偏移的距离Fig.7.Movement of the convergence zone after considering the earth curvature.

第4 个上反转点会聚区(传播距离约为232 km)约前移2.5 km、下反转点会聚区(传播距离约为204 km)约前移2.3 km,第9 个上反转点会聚区(传播距离约为524 km)约前移5.5 km、下反转点会聚区(传播距离约为495 km)约前移5.4 km,第16 个上反转点会聚区(传播距离约为932 km)约前移9.6 km、下反转点会聚区(传播距离约为902 km)约前移9.7 km,见表2.此外,考虑地球曲率后上反转点会聚区的深度变化不大,下反转点会聚区的深度变浅,约变浅42 m.产生差异的根本原因是水声场射线几何拓扑结构的改变.

表2 考虑地球曲率后会聚区向声源方向前移距离Table 2.Distance of convergence zone moving forward towards sound source after considering the earth curvature.

应当指出,现有研究[16,17]均是采用环境参数修正的方法考虑地球曲率的影响,考虑到球面与平面存在本质不同,即无等距映射,因而将问题先转化为欧氏空间计算、再加以曲率修正的方法,客观上将存在一定的误差.本文通过直接在弯曲底流形上建模,避免了曲率修正带来的误差.

以0°掠射角声线反转点的间距作为会聚区的距离,仿真结果显示地球曲率修正前会聚区距离约为58.15—58.34 km,地球曲率修正后会聚区距离有所增大,约为58.82—58.87 km.基于已经得到的会聚区位置,本文分别计算了200 和4000 m 接收深度处会聚区的宽度(定义见第3 节),见图8.从图8 可以看出,Munk 声速剖面近海面处的会聚区宽度随声传播呈现先变大后变小的现象,最大约20 km,最小约4 km.与图6 中呈现的会聚区结果相吻合.会聚区的宽度受Jaocbi 场Y1和传播距离的共同制约 ((21)式),当传播距离较小时,雅可比场|Y1| 的极大值也较小(图3),会聚区条件(21)式容易满足,会聚区较宽;当传播距离较大时,雅可比场|Y1| 的极大值较大(图3),由(21)式可以看出,雅可比场|Y1| 较小时才可满足会聚区条件,此时会聚区的宽度变窄.

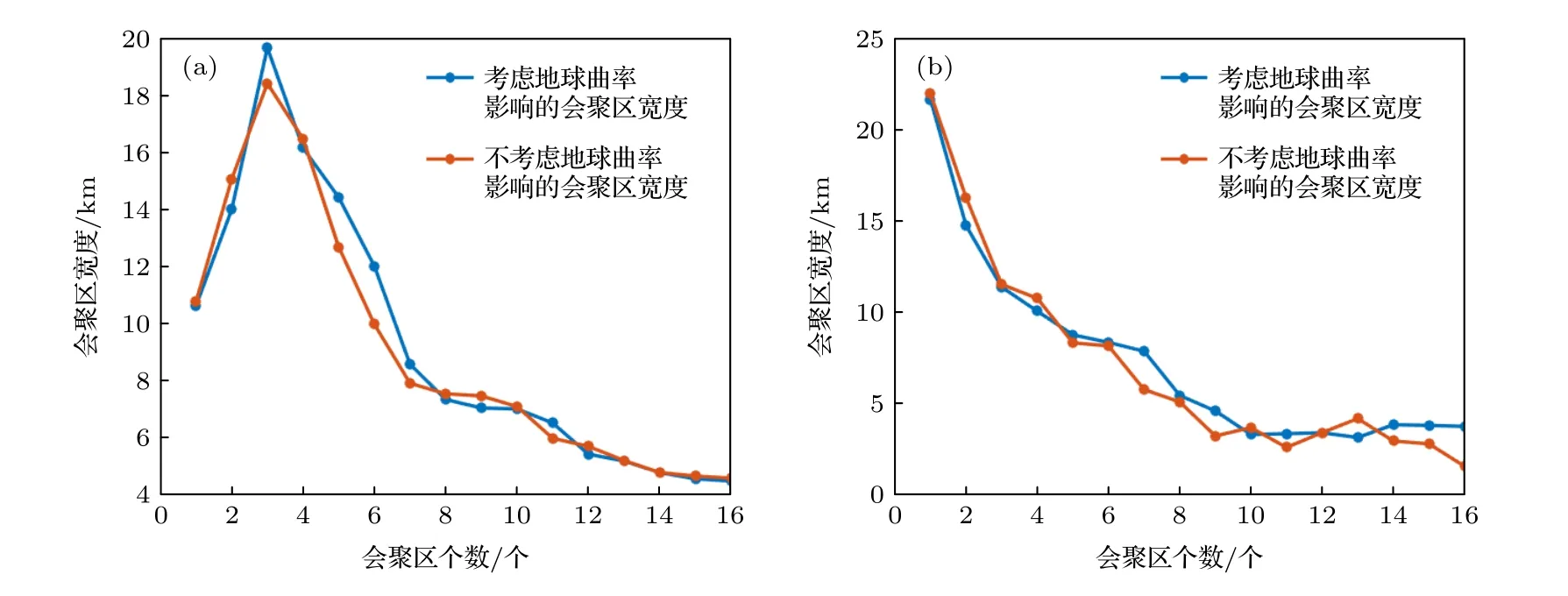
图8 不同接收深度处考虑地球曲率和不考虑地球曲率的会聚区宽度 (a) 200 m;(b) 4000 mFig.8.The width of convergence zone considering and not considering earth curvature at the two different receiver depths:(a) 200 m;(b) 4000 m.

4.3 声传播损失阈值对深海会聚区的影响分析

当会聚区几何扩展损失的阈值β改变时,会聚区的宽度也随之改变,如图9.从图9 可以看出,β越大,会聚区声线的聚焦效果越强,会聚区的声强越大,但会聚区的宽度减小.β变小,会聚区的宽度变大,但会聚区内的声强变弱.当β=25 dB 时,200 m 接收深度处第7 个上反转点会聚区的宽度约7 km,β=20 dB 时 约9 km,β=15 dB 时 达到30 km.

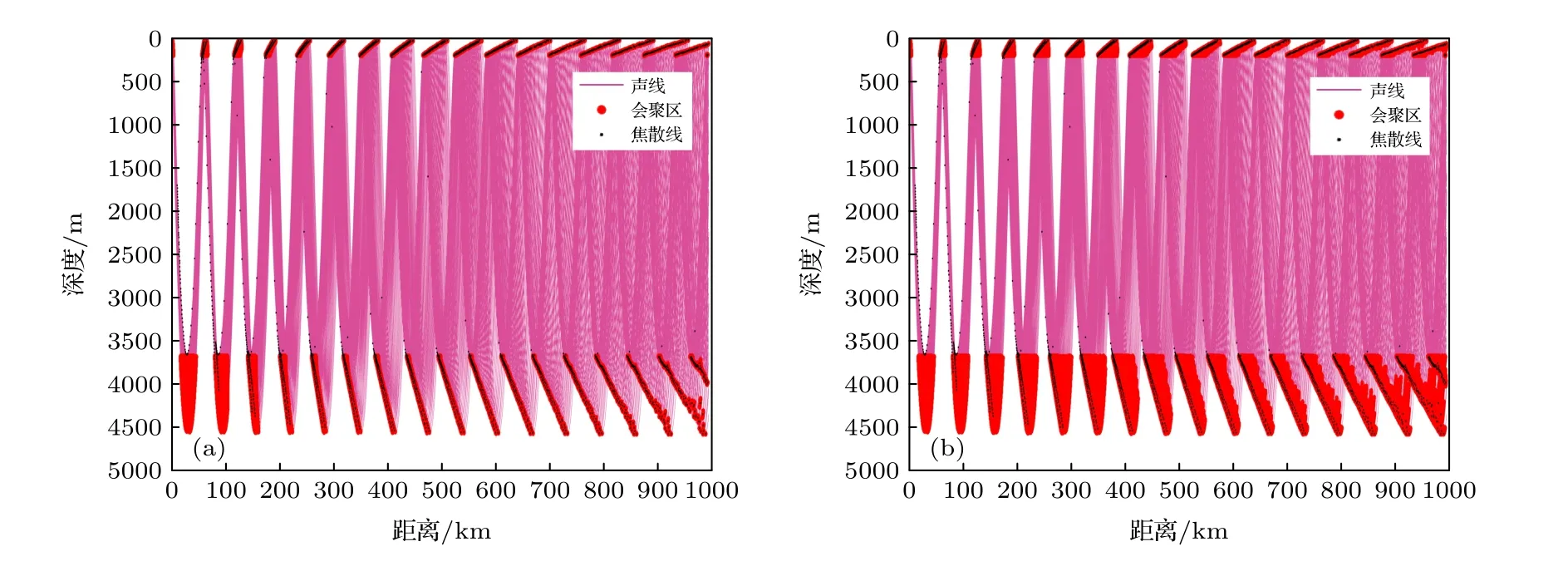
图9 不 同几何扩展损失阈值下的会 聚区 (a) β=25 dB;(b) β=15 dBFig.9.Convergence zones at two different geometric spread loss thresholds β : (a) β=25 dB;(b) β=15 dB.

图10 给出了声源深度为150 和300 m,其他参数不变时考虑地球曲率影响后的焦散线和会聚区位置.可以看出此时仍会形成明显的上、下反转点会聚区,声源越深,上反转点会聚区的深度越深,下反转点会聚区的深度越浅.声源深度为150 m时上反转点会聚区的深度约为20—150 m,下反转点会聚区的深度约为3890—4700 m.300 m 时上反转点会聚区的深度约为100—300 m,下反转点会聚区的深度约为3260—4150 m.

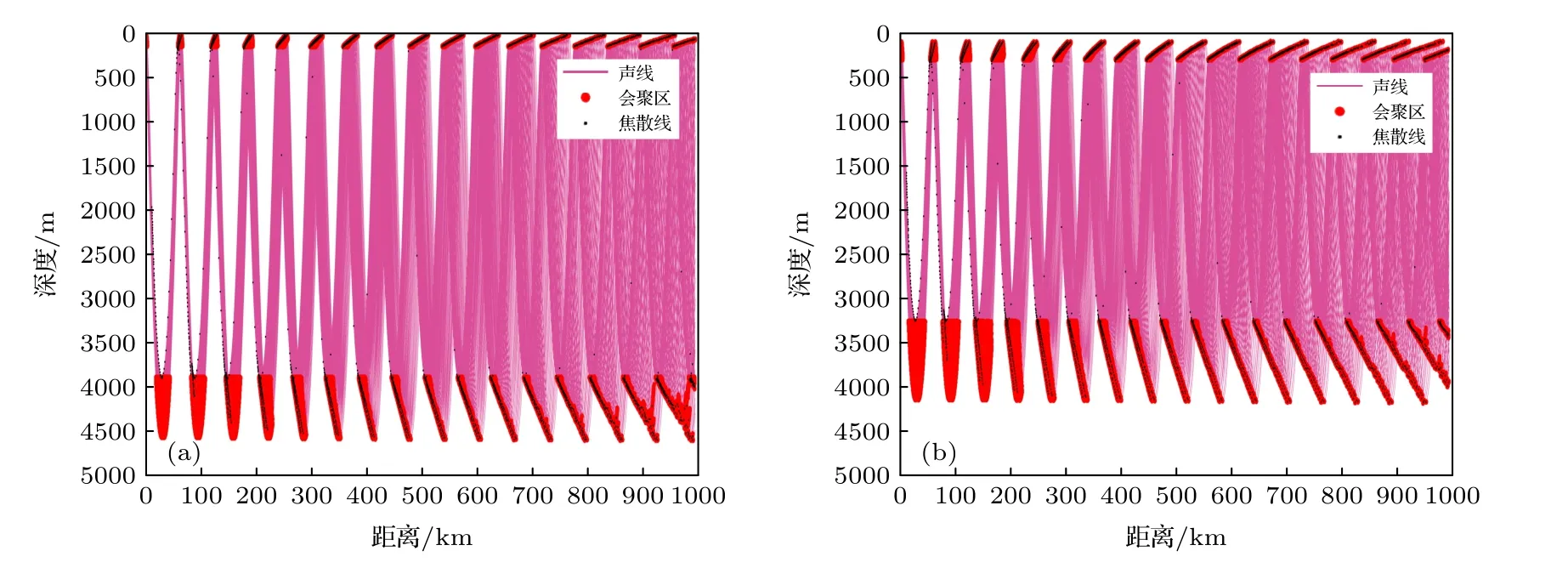
图10 不同声源深度的焦散点与会聚区 (a) 150 m;(b) 300 mFig.10.Convergence zones at two different source depths: (a) 150 m;(b) 300 m.

4.4 黎曼几何模型与简正波方法的对比验证

为验证本文结果的正确性,本文使用未考虑地球曲率的经典简正波理论对会聚区进行了预报.定义上下反转区域内声传播损失小于最大损失40 dB的区域为会聚区,图11 给出了环境参数保持不变时,使用简正波声场模型(Kraken)计算的Munk声速剖面声传播损失及会聚区仿真结果.

从图11 可以看出,在均不考虑地球曲率影响的情况下,使用简正波方法预报的会聚区的距离、宽度等特征与本文黎曼几何建模计算结果一致,可以从侧面验证本文会聚区黎曼几何模型的有效性.此外,本文通过共轭点、雅可比场、截面曲率等几何概念建立会聚区模型,给出了可自然考虑地球曲率效应的会聚区精确计算方法,在黎曼几何框架下揭示了深海会聚区的数学物理机理,相比难以直接考虑地球曲率效应的经典水声建模理论具有明显的优势.

图11 黎曼几何与简正波法计算的会聚区对比图 (a) 黎曼几何理论计算的会聚区 (b) 简正波法(Kraken 软件)计算的会聚区Fig.11.The convergence zones by Riemann-Geometry and Normal-Mode theory: (a) Based on Riemann-Geometry Theory ;(b) based on Normal-Modes (Kraken).

5 结论与展望

本文将地球曲率的影响考虑在内,基于水声射线建模的黎曼几何理论描述建立了深海远程声传播射线模型,分析了形成会聚区的物理机理,给出了会聚区的黎曼几何描述.主要结论如下:

1) 在弯曲球体流形上直接建立深海会聚区几何模型,可自然地考虑地球曲率效应;结合深海会聚区物理特性分析,给出其黎曼几何描述,初步建立了深海会聚区的黎曼几何学概念.

2) 本文的考虑地球曲率的会聚区黎曼几何模型具有精确性特征,相比间接修正类方法而言,避免了参数修正带来的误差;考虑地球曲率后的截面曲率增加了一个附加项,本质上改变了水声射线拓扑结构,对会聚区产生实质影响.

3) 采用Munk 声速剖面的会聚区黎曼几何模型仿真计算显示,近海面处的会聚区宽度随声传播呈现先增大后减小的现象,最大约20 km,最小约4 km.同时,考虑地球曲率影响后声线、焦散点和会聚区均向声源方向前移.传播距离越大,会聚区前移的距离也越大.声源和接收深度均为200 m时,第16 个上反转点会聚区(传播距离932 km)约前移9.6 km.

本文选择深海会聚区远程声传播作为研究对象,是非欧几何在水声学应用研究的初步探索.后续还有很多工作有待深入开展: 1)本文仅考虑地球曲率恒定时的深海远距离会聚区传播.对实际两极稍扁、赤道略鼓的不规则真实地球而言,需要研究考虑真实地球模型的黎曼几何会聚区建模;2)考虑更多真实海洋环境复杂因素的黎曼几何水声建模研究与应用,如同时考虑地球曲率和海流偏转效应、基于伪黎曼流形的时变大范围声场传播建模,表面声道远程声传播机理等.

感谢宋君强院士对该研究探索的鼓励和支持,黄思训教授、梁湘三教授审阅了论文初稿,特致谢忱.