基于有限元的电力变压器抗短路能力校核方法研究

罗竣匀， 刘 君， 胡 晓， 徐舒蓉

(1.贵州大学电气工程学院， 贵州 贵阳 550025； 2.湖南大学电气与信息工程学院， 湖南 长沙 430002； 3.贵州电网有限责任公司研究生工作站， 贵州 贵阳 550002； 4.贵州电网有限公司电力科学研究院， 贵州 贵阳 550002)

1 引言

变压器作为电力系统中的重要电气设备，能否长期维持在安全稳定的运行状态将直接影响供电可靠性。而实际运行期间变压器会承受多次短路电流冲击，易促使绕组线圈变形、绝缘老化或破损等情况发生。有统计表明，变压器抗短路强度不足诱发事故的比例约占总量的35%[1,2]。尽管变压器在设计时已经要求可承受最严重工况下短路电磁力冲击，但随着运行年限增高，仍可能会出现绕组塑性变形、错位或坍塌等现象[3]。因此，有必要分析研究变压器的抗短路能力及其影响因素，为实际工程中变压器的设计和校核提供参考。

变压器抗短路校核方法主要有IEC标准计算、国标计算(GB 1094.5—2008)、日本变压器专业委员会和国际大电网会议方法等。IEC计算方法主要是考虑短路电流的类型和持续时间，针对变压器因短路电流产生的动态力进行校核[4]；此外，考虑导线受力面积、材料、结构以及支撑情况等边界条件，并采取一定的安全裕度来考核绕组的稳定性，但是该方法在不同线规下的计算结果会有一定差异；国标计算方法根据电网的具体情况，将不同额定容量及电压等级的短路阻抗值和短路视在容量纳入考虑范围[5]，但是由于变压器结构复杂，在轴向极限倾斜力的计算上存在极限性和不确定性[6]；日本变压器专业委员会的计算方法是以塑性理论为基础，由薄壁圆筒承受辐向压力的稳定性公式推导而来[7]，将导线的结构、绕制方式和实际支撑的撑条数考虑进辐向校核方法，但是该方法是基于静态模型推算公式，文献[8]结果显示其不适合已发生辐向失稳的变压器校核；国际大电网会议方法提出各指标的校核模型，并且考虑“自由翘曲”和“强制翘曲”两种辐向失稳模型，为校核工作提供模型基础[9]。

文献[10]从短路校核、系统运行和试验情况三个方面，建立了电力变压器抗短路能力综合评估基本框架。本文通过整理分析绕组结构稳定性指标，结合GB 1094.5—2008《电力变压器 第5部分：承受短路的能力》给出的评估条件，总结并改进抗短路能力理论校核方法。利用有限元仿真软件可精确计算磁通密度的优点[11,12]，搭建变压器二维有限元仿真模型，计算出漏磁通密度和短路电磁力分布，并结合应力计算指标给出校核结果，最后将校核结果与专业软件计算结果和变压器返厂解体情况进行对比验证，说明该改进校核方法的有效性。

2 绕组结构稳定性关键应力指标解析算法

2.1 变压器轴向稳定性计算

由于绕组受到短路电磁力作用，在绕组内部会产生机械应力。当绕组内部应力值小于铜导体的屈服强度时，绕组内部只存在可恢复的弹性变形[13,14]。当绕组内部应力值大于绕组的屈服强度时，就会发生不可恢复的塑性变形。

2.1.1 垫块和导线之间的轴向弯曲应力

由于弯矩过大，使得垫块之间的绕组不同程度地弯曲变形，如图1(a)所示。

求取轴向间的最大弯曲应力可将两个垫块之间的导线线段看作两端固定支点的梁[15,16]，长度为L的线段上受均匀载荷q的轴向力，如图1(b)所示，求取弯曲正应力时需要先求导线截面z轴上的惯性矩Iz和弯矩M。当导线是常规导线或者非自粘导线时，b和h分别为单股导线的辐向宽度和轴向高度。当导线是自粘换位导线时(如图2(a)所示)，b取b1(n1+1)/2，n1为子导线的股数，h为单根子导线的轴向高度之和，即2h1，b1和h1分别为单根子导线的辐向宽度和轴向高度。

图2 导线横截面示意图Fig.2 Schematic diagram of cross section of conductor

取平行于z轴且高度为dy的矩形为微元面积dA,则惯性矩Iz为：

(1)

参考文献[17]列出了该模型的总弯矩并推算出了轴向弯曲公式如下所示：

(2)

式中，FY为线饼受到的平均轴向力，N；k1为导线系数，对于常规导线和非自粘导线取1，对于自粘换位导线，取0.8；N为每饼的匝数乘以并联的导线根数；R为绕组的平均半径，mm；Z为垫块档位数；K为垫块的宽度，mm。

由于式(2)没有考虑两端弯矩共同作用的情况，因此需要对x处的弯矩公式进行改进。考虑到导线两端的垫块相同具有对称性，所以弯矩Ma=Mb，在x处产生的弯矩为：

(3)

由参考文献[15]可查该固定梁最大的弯矩为Ma=qL2/12，代入式(3)可得：

(4)

当x=L/2时，M(x)取到最大值得qL2/24，此时最大弯曲正应力为：

(5)

(6)

式中，M为梁所受的弯矩；y为中心层以下或以上的高度。

其中，等效为梁的两垫块之间导线距离L为：

(7)

将式(6)、式(7)代入式(5)可得出改进后的导线轴向弯曲应力计算公式为：

(8)

根据GB 1094.5—2008《电力变压器 第5部分：承受短路的能力》规定，在辐向垫块之间的跨度内的导线轴向弯曲应力应满足：σba.act≤0.9Rp0.2,Rp0.2为导线的屈服强度值。

2.1.2 单个垫块轴向压缩应力

在线圈中导线纸绝缘和辐向垫块的压缩应力为：

(9)

式中，FY.max为轴向最大电磁力，N；AZ为单个垫块面积，mm2。导线为纸绝缘时，辐向垫块的压缩力应满足：σsp.act≤80 MPa。

2.1.3 绕组轴向倾斜

当实体绕组受到过大的轴向压缩力时，可能会出现辐向绕组整排导线往一个方向倾斜，此时子导线在导线截面内发生倾斜，如图2(c)所示。

导线自身抗倾斜极限力与导线材料、线规以及绕组的尺寸等参数有关，导线的抗倾斜能力和导线的弹性模量、线规大小以及并绕根数成正比，和线圈的平均直径成反比，其表达式为[18]：

(10)

式中，Kll为绕组系数；E为导线的弹性模量；irr为导线的辐向根数；Irr为导线辐向并绕根数；D为线圈的平均直径。

在GB 1094.5—2008中指出对于采用导线或非自粘性的换位导线卷制成的连续式、螺旋式和层式绕组，其最大轴向压缩力及倾斜时的极限值为：

(11)

式中，E0为铜的弹性模量，取值为1.15×105MPa；K1为扭曲项系数；K2为分层叠置系数，N/mm3；K3为计及铜工作硬度等级的系数；K4为计及动态倾斜的系数；n为绕组辐向宽度中导线数；γ为导线形状常数；X为连续式、螺旋式绕阻的垫块覆盖系数。

2.2 变压器辐向稳定性计算

当电流通过线圈时，在线圈所处空间和附近产生磁场。由洛伦兹力原理可知，线圈附近的轴向漏磁通和辐向漏磁通分别与短路电流共同作用产生辐向短路电磁力和轴向短路电磁力，且电磁力的大小和漏磁场的磁通密度、通过导线的电流以及导线的长度有关。辐向电磁力会使高压线圈受到往外拉伸的力，低压线圈受到向内压缩的力，所以最后会将绕组间主空道的绝缘距离扩大[19]。图3为内外线圈的受力情况。

图3 内外线圈受力情况Fig.3 Internal and external coils under force

2.2.1 线圈的平均环形拉伸、压缩应力

辐向电磁力将外线圈沿半径向外拉伸，线圈的半径就有扩大的趋势，线圈靠自身的强度来抵抗辐向电磁力的作用，因此线圈在辐向上形成环形拉伸应力。如果拉伸应力过大超过导线的屈服强度，会产生残余应力使导线的绝缘破裂或是绕组发生局部翘曲[20,21]。

辐向电磁力会将内线圈沿半径向内收缩，线圈的半径就有缩小的趋势，当压缩应力超过线圈所能承受的范围，则内线圈发生失稳形变。环形压缩应力会使得线圈发生翘曲变形或者弯曲变形，弯曲是由于两个内撑条之间的导线作为梁因弯矩过大而产生的永久变形，且这种变形通常为对称变形。内线圈经常由于翘曲现象而失稳，翘曲分为自由翘曲和强制翘曲。自由翘曲模式被认为是无支撑的故障类型，即在内线圈的内表面没有任何约束，如图4(a)所示。强制翘曲模式是被认为线圈内部的支撑结构为绕组提供足够刚度，在相邻撑条之间翘曲是对称向内的，如图4(b)所示。

图4 线圈辐向变形的类型Fig.4 Types of coil spoke deformation

外、内线圈的辐向平均环形拉伸、压缩应力为[22]：

(12)

式中，FR为线饼所受平均辐向力，N；A1为线圈每饼绕组截面积，cm2；s1为单根导线横截面积，cm2；m1为每匝线饼并联分支数；n2为导线辐向并联根数；W为绕组总段数。应力计算单位为kg/cm2，再除以10单位即为MPa，若FR的单位为N，则面积单位取mm2。

现有可参考的平均环形应力计算公式中，即式(12)中W通常取绕组总匝数的值，在计算该指标时容易因绕组结构形式不同而出现误差。根据材料力学正应力公式定义(σ=F/S)，当FR是根据洛伦兹力原理(F=BIL)计算时，应考虑绕组结构形式的影响，受力面积S应取通过电流I的导线截面积。现对该公式取值作改进：当绕组结构型式为螺旋式时，W为绕组总段数或总匝数；若为内屏连续式等饼式线圈时，W取绕组总段数。

对于连续式绕组、螺旋式绕组及多层式绕组中每一层上的平均环形拉伸应力需满足：σact≤0.9Rp0.2。

对于常规导线和非自粘性连续换位导线的连续式绕组、螺旋式绕组及多层式绕组上的平均环形压缩应力需满足：σact≤0.35Rp0.2，对于自粘性连续换位导线需满足：σact≤0.6Rp0.2。

2.2.2 撑条和导线之间的辐向弯曲应力

绕组线圈的装配过程中，在磁心和绕组内线圈之间的空间，会留出装配缝隙给径向支撑条。如果贴合度不够，在运行中产生振动则难以保证撑条对导线的有效支撑，特别是内线圈受到的辐向电磁力更大，容易发生辐向弯曲从而引起绕组整体失稳。

位于撑条和导线之间的辐向弯曲应力推导过程同式(8)，计算公式为：

(13)

在撑条或垫块之间的跨度内的导线辐向弯曲应力应满足：σbr.act≤0.9Rp0.2。

3 变压器抗短路能力理论校核计算

整体校核流程如图5所示，其中在国际大电网会议中乌克兰扎布罗热变压器研究所(Ukrainian Research, Design and Technological Transformer Institute, VIT)开发的变压器短路校核模块(WELDINST)上的校核计算精度得到认可[5]，为验证此次仿真结果的准确性，采用计算结果与VIT计算方法结果相对比。

图5 变压器结构稳定性校核流程Fig.5 Transformer structural stability verification process

根据表1和表2给出的该三绕组变压器的主要铭牌值、几何参数和绕组参数,使用Comsol Multiphysics有限元软件建立110 kV变压器的二维模型。为计算便捷，在建模设置做出以下假设：

(1)由于变压器的对称特点，仅对高、中、低压三绕组进行二维轴对称建模，且忽略调压绕组的影响。

(2)忽略对磁场影响较小的结构件，如压板、端圈和出头引线。

基于表1、表2数据进行仿真计算，得出绕组的漏磁分布，根据电磁耦合计算出绕组轴向和辐向电磁力分布，仿真结果均用于校核计算，最后用应力解析算法校核该变压器的抗短路能力。

表1 变压器电气及结构参数Tab.1 Transformer electrical and structural parameters

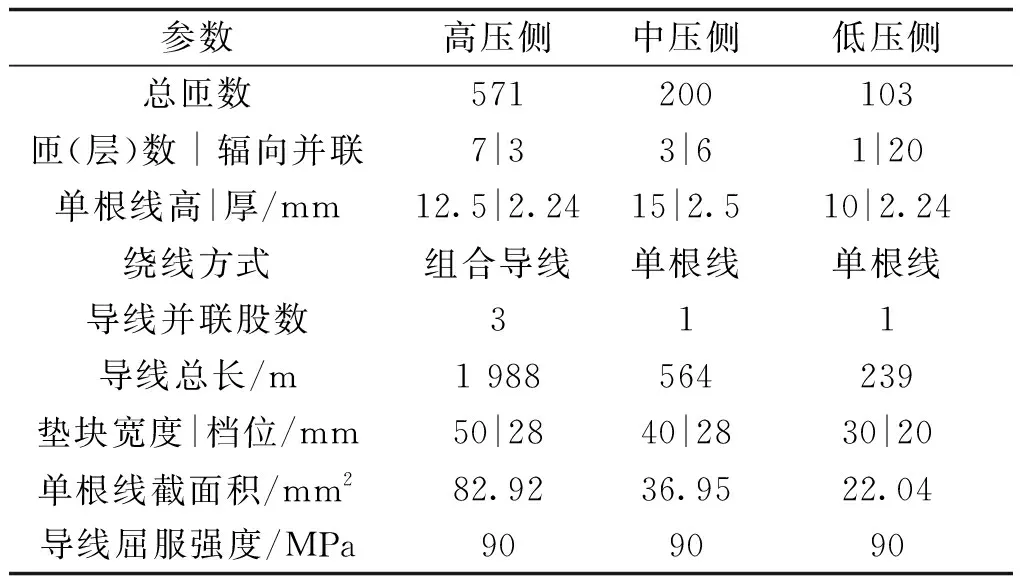
表2 线圈结构参数Tab.2 Coil structure parameters

3.1 模型验证

根据磁场储能原理，可通过外加激励产生的磁场能求出变压器的短路阻抗，表达式为[23]：

(14)

式中，Uk为短路阻抗百分数，%；f为工作频率，Hz；Wm为总磁能，J；Sn为变压器单柱容量，V·A。

通过建立有限元模型，计算不同运行方式下的总磁能，最后得到模型的短路阻抗仿真值与变压器额定阻抗相对比(表3)，以验证模型的可靠性。

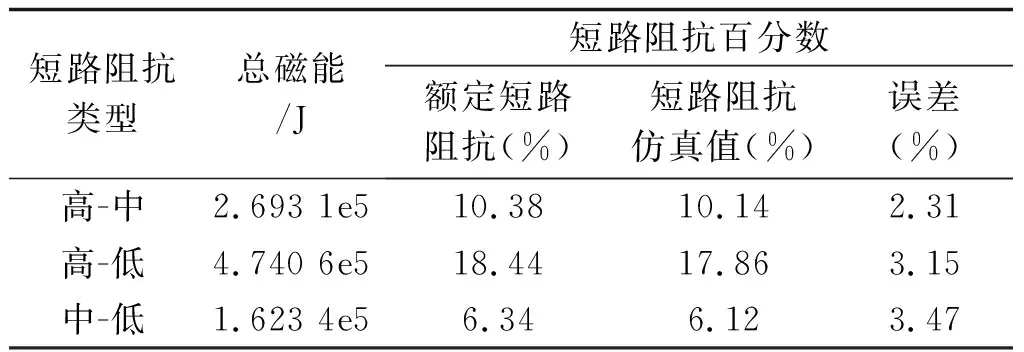
表3 阻抗计算误差对比Tab.3 Impedance calculation error comparison

对比结果表明，用二维轴对称模型计算短路阻抗与变压器额定分接阻抗的误差均在3.5%内，误差与网格剖分方式和大小相关，故该模型可作为短路校核的计算模型。

3.2 短路电流计算与电流激励选取

当变压器负荷侧发生三相对称短路时，合闸角为0°时产生最大峰值电流，瞬时电流为[24,25]：

(15)

式中，Im为短路电流峰值，A；α为合闸角；ω为电压的角频率；Rk、Lk分别为系统的短路电感和电阻。

根据标准GB 1094.5—2008要求，110 kV和38.5 kV侧的系统短路容量分别为9 000 MV·A和1 500 MV·A，峰值系数取2.55。选取最符合实际工况的四种运行方式，短路电流有效值见表4，运行方式1～4分别为高压侧运行-中压侧出口三相短路(HV-LV)、高压侧运行-低压侧出口三相短路(HV-LV)、中压侧运行-低压侧出口三相短路(MV-LV)、高+中压侧运行-低压侧出口三相短路(H+M-LV)。

表4 不同运行方式的短路电流有效值Tab.4 RMS value of short-circuit current for different operating modes

算例中变压器在2021年5月各遭受了两次近区短路故障，一次为35 kV侧B相和C相短路故障，中压绕组遭受的短路电流有效值为5.87 kA，持续时间为0.36 s。另外一次为10 kV侧 abc三相短路故障，低压绕组遭受的短路电流有效值为26.16 kA，持续时间为0.38 s。中压、低压绕组实际遭受的短路电流与按照GB 1094.5—2008理论计算短路电流偏差分别为0.3%和8.5%，偏差较小。

因此，高压、中压线圈按照运行方式1进行考核，低压线圈按照运行方式2和运行方式4进行考核，不同工况下的激励电流按照表4选取。

选取短路电流最严重工况，即变压器在高中额定运行，低压侧三相对称短路时为例，经过半个周期(即t=0.01 s时)后短路电流达到峰值，随后逐渐衰减，其衰减速度由衰减时间常数决定。流过该算例线圈的短路电流如图6所示。

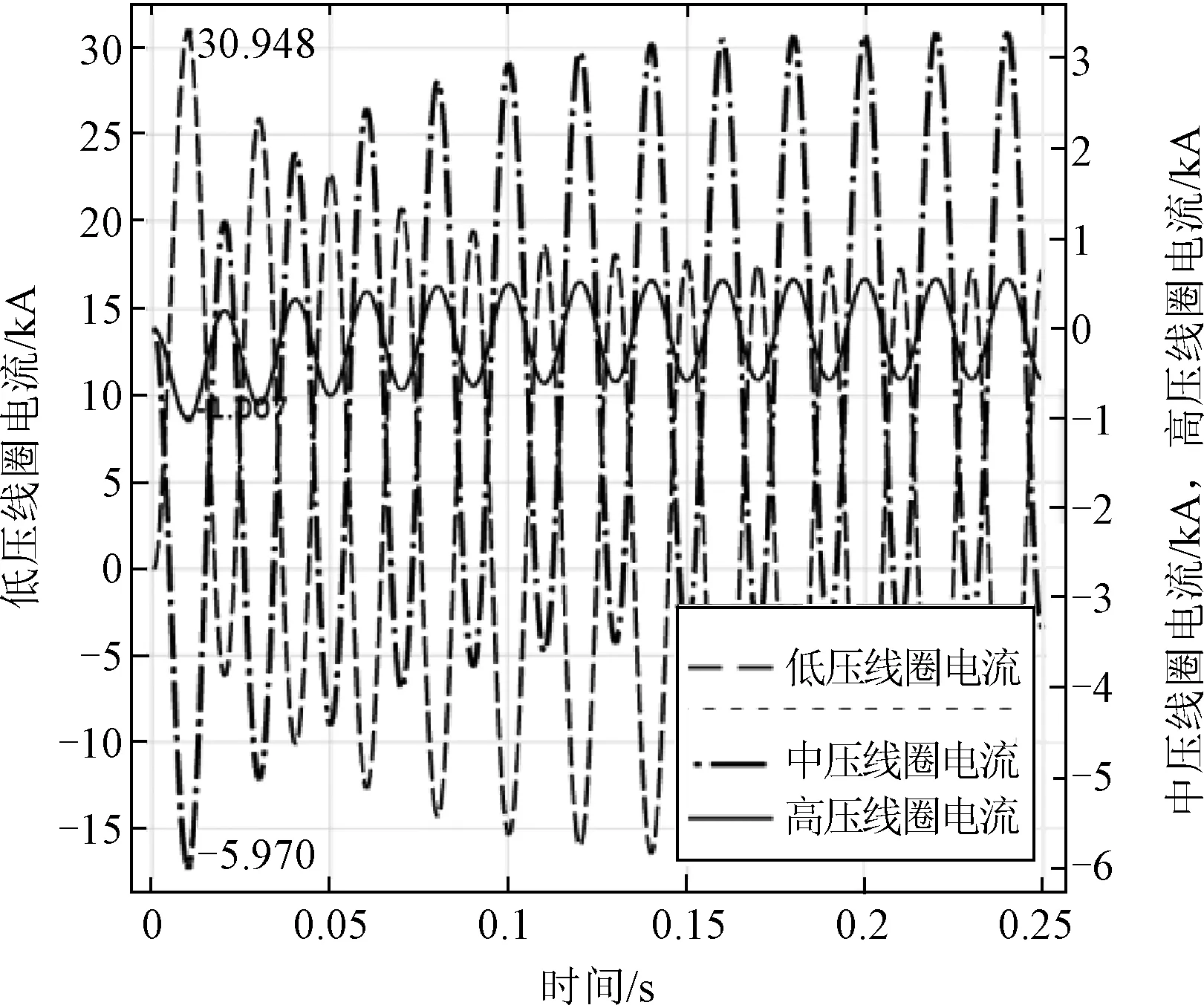
图6 三绕组变压器的短路电流Fig.6 Short-circuit current of a three-winding transformer

3.3 漏磁场仿真计算

根据变压器的参数尺寸建立二维轴对称模型，选取变压器一相的剖面建模，在0.01 s时绕组附近的漏磁场分布如图7所示，漏磁通的密度模最大值出现在绕组之间的空道中，值为2.5 T左右。

图7 漏磁场分布云图Fig.7 Leakage field distribution

在0.01 s时线圈内外的辐向和轴向漏磁通密度分布如图8所示，可知漏磁通密度的分布和电磁力分布有相似的分布特点。由于中压线圈内外侧的受力大小相似，故仅展示出中压内侧的受力曲线，各线圈的最大漏磁通密度见表5。

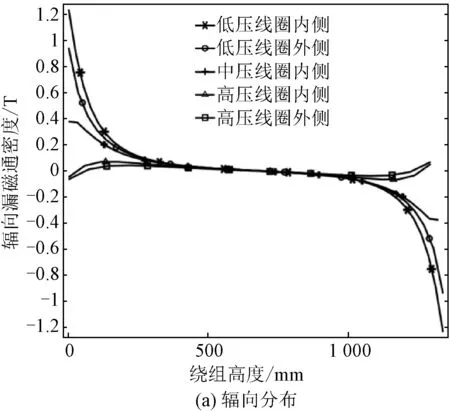
表5 线圈最大漏磁通密度值Tab.5 Coil maximum leakage density value

3.4 短路电磁力密度计算

图9为各绕组的内外侧电磁力密度对比曲线。从图9(a)可看出，高压绕组受到往外拉的力，低压绕组受到往铁心方向压缩的力；中压绕组中部所受的辐向受力最大，电磁力密度达到1.39×107N/m3，低压绕组内侧中部所受的辐向受力最大，电磁力密度达到3.68×107N/m3。从图9(b)可看出，在轴向上，绕组的端部受力基本呈轴对称分布，且方向相反；中压绕组所受最大轴向受力点的电磁力密度约为2.95×106N/m3，低压绕组内侧所受最大轴向受力处电磁力密度约为2.53×107N/m3，且分布在绕组两端。

据洛伦兹力的原理，线圈所受到的辐向和轴向电磁力的计算为：

(16)

式中，FR、FY分别为辐向和轴向电磁力，N；Br、By分别为辐向和轴向漏磁通密度，T；L1为垂直于磁场方向的导线长度，m。

3.5 抗短路能力理论校核计算与对比

将各个指标进行计算并与国标许用值进行对比，以校核该变压器算例的抗短路能力。根据材料力学原理，每个实体绕组的最大压缩力是结合仿真结果计算得出，计算公式为：

σ1=10-3Fy.maxAZZ

(17)

校核计算的结果见表6，计算结果表明：

(1) 中压线圈在高对中运行工况下，中压侧发生三相短路时，内线圈平均环形压缩应力超GB 1094.5—2008许用值，辐向稳定性不满足国标要求，易发生辐向失稳。

(2) 低压线圈在高+中对低的运行工况下，低压侧发生三相短路时，内线圈平均环形压缩应力指标超GB 1094.5—2008许用值，辐向稳定性不满足国标要求，易发生辐向失稳。

(3) 高压绕组、中低压绕组的其他稳定性指标满足国标要求。仿真计算值与WELDINST计算值的最大差异在20%以内，与文献[9]中不同方法之间计算结果的差异水平相近，在工程计算可接受的范围内。

表6 校核计算结果Tab.6 Calibration calculation results

4 变压器解体验证

解体情况(如图10所示)可知，中压绕组三相在辐向上存在严重的自由翘曲变形，端部存在不同程度的轴向倾斜变形，特别是在中压C相中部换位处，出现匝绝缘和换位垫纸因局部放电而碳化变黑痕迹。这和中压绕组采用普通组合导线、电磁线宽厚比过大、只设置内撑条的结构设计有关。该变压器为2003年出厂，电磁线屈服强度设计值≤90 MPa，在电磁线自身强度不够的条件下，未采用更多的加强措施，绕组易发生失稳。低压绕组b、c相在辐向上也存在明显的自由翘曲变形，特别是b相绕组。

分析可知，变压器实际失稳表现与抗短路能力理论校核结果相吻合。在发生短路时辐向线圈容易发生翘曲现象，从而可能导致绕组线圈失稳。辐向弯曲强度不足，则可采用屈服强度较大的导线、增大导线的横截面积、增加撑条数量或加固撑条以防止位移等措施来增强线圈的辐向稳定性。

5 结论

本文利用有限元仿真结合改进后的变压器绕组稳定性校核方法，对某110 kV三绕组变压器进行了短路校核计算，并对校核结果进行了对比分析和变压器返厂解体验证，得到如下结论：

(1) 不同校核体系计算结果存在一定的偏差，与磁通密度、导线长度的选值有关。但辐向校核应重点考察线圈中部的辐向弯曲强度，轴向校核应重点考察端部处的轴向弯曲强度以及实体绕组的最大压缩力原则不变。

(2) 轴向弯曲应力计算模型等效为两端固定支点梁模型时，应考虑两端弯矩共同作用对弯曲应力的影响。

(3) 平均环形和压缩应力计算应考虑绕组结构型式的影响，当绕组结构型式为螺旋式时，W为绕组总段数或总匝数，若为内屏连续式等饼式线圈时，W为绕组总段数。

(4) 按照本文提出校核流程和算法，对一台110 kV三绕组变压器进行了校核验证，并与WELDINST校核结果进行了对比，偏差范围为1.7%～18.4 %，在工程计算可接受范围内。

(5) 变压器返厂解体发现弯曲强度不合格的绕组均存在翘曲变形的情况，验证了WELDINST校核算法和本文所提校核方法的准确性，证明所提校核方法具备工程应用价值。