基于改进型匹配滤波的非稳态电能质量信号分析方法
杨金东, 吴万军, 唐立军, 杨子龙
(1. 云南电网有限责任公司电力科学研究院, 云南 昆明 650214; 2. 云南电网有限责任公司迪庆供电局, 云南 迪庆 674499; 3. 中国科学院电工研究所, 北京 100190)
1 引言
随着可再生能源发电的快速发展应用,风电、光伏、储能等设备的装机规模越来越大,其容量在电网装机中的占比不断提高[1-3]。绝大多数可再生能源发电通过电力电子设备并入电网;同时轨道交通、电动汽车、工业和民用变频/调速器等非线性负荷也采用电力电子设备接入配电网,使得电力系统“源-网-荷”各部分的电力电子化程度不断加深。电力电子设备的大量使用导致电力系统内暂态振荡、电压闪变等非稳态扰动成分含量不断增加,严重影响了供电可靠性和电能质量[4,5]。
电力系统中存在着多种电能质量扰动,如稳态谐波、电压闪变、电压骤升骤降、电压脉冲、暂态振荡等成分[6]。其中,对于谐波等稳态成分可采用傅里叶变换、小波变换、谱估计等方法实现电能质量稳态谐波幅值频率等参数的在线估计,分析结果可用于谐波源的定位与治理等[7,8]。但是对于暂态振荡、脉冲等非稳态电能质量扰动成分,傅里叶变换等方法很难对其进行全面分析和参数准确估计[9],因此,需要研究提出新的分析方法实现电能质量非稳态扰动信号成分的完整提取与分析,为电网电能质量的治理提供依据。
常见的非稳态电能质量信号分析方法有时域分析、频域分析和时频域分析等,其中小波变换是常用的时频域分析方法,通过伸缩平移运算对电能质量信号进行多尺度分解,可聚焦到扰动信号的任意细节。由于小波变换划分频带时一般会产生频谱混叠和泄漏现象,从而降低了小波变换对非稳态电能质量扰动分析的准确度[10];此外,小波变换按频带将电能质量稳态成分和非稳态成分一起处理,难以逐个得到处于同一频带内的多个扰动成分的识别和参数估计的准确结果。
为了提高对非整数次谐波和非稳态电能质量扰动成分分析的准确度,国内外学者尝试采用了多种信号分析方法,如时频原子变换法、滤波器组法、希尔伯特-黄变换法、基于Cohen类的时频法以及经验小波法等[11,12],并取得了一些研究成果。但是,随着电网组成结构的日益复杂,复合扰动、间谐波、非稳态干扰等问题给上述信号检测方法的应用带来挑战。对此,文献[13]提出将匹配滤波应用到电能质量信号分析方面,实现电能质量间谐波分析和扰动特征的提取,为电能质量非稳态扰动的分析提供了一个可行方法。
匹配滤波是一种重要的信号处理方法,广泛应用于通信、雷达、水声及物探等测量测试系统中。匹配滤波是指经过滤波后,滤波器输出端的信号瞬时功率与噪声平均功率的比值最大,即信噪比(Signal to Noise Ratio,SNR)。当有用信号与噪声同时进入滤波器时,有用信号在某一瞬间出现尖峰值,而噪声信号则受到抑制[14,15]。因此,无论是在时域还是在频域,匹配滤波都能保证通过滤波环节的有用信号尽可能强,噪声则被尽可能地衰减。
在电能质量分析领域,常规的匹配滤波算法是通过对原始电能质量信号的多次相关运算来实现各次稳态谐波和非稳态扰动成分的分析和分离,由于是对被分析信号的稳态和非稳态扰动成分不加区分地进行处理,因此很难准确分析幅值较小的稳态谐波参数以及较微弱非稳态扰动成分的组成[16-18]。为了克服这个不足,本文提出非稳态电能质量信号的改进型匹配滤波分析方法,采用正弦基函数对电能质量信号中的稳态成分进行匹配滤波分析,分离稳态谐波和非稳态扰动成分,使电能质量非稳态扰动的识别和参数估计得以实现。通过对给定的电能质量信号算例进行分析,证明所提出方法的有效性。
2 电能质量信号的匹配滤波方法
2.1 改进型匹配滤波方法原理
改进型匹配滤波采用过完备的冗余时频基函数集,通过内积运算来确定信号的组成成分并分离扰动成分,实现电能质量信号扰动分析和参数估计。
改进型匹配滤波算法首先对正弦函数g(t)按照式(1)进行伸缩、平移和调制等操作得到一系列时频基函数,这些时频基函数的完备集合构成了冗余时频基函数集D,即:
(1)

对连续时间信号f(t)∈H(H表示Hilbert空间)进行改进型匹配滤波分析处理。首先从冗余时频基函数集D中选择与信号f(t)最为匹配的基函数g0(t),即g0(t)与函数f(t)的内积是基函数集D中所有时频基函数最大的,则信号f(t)被分解成:
f(t)=〈f(t),g0(t)〉g0(t)+Rf(t)
(2)
式中,〈·,·〉为时间函数的内积运算;Rf(t)为信号f(t)经第一次匹配滤波分解后的残余信号。
按照式(1)、式(2)对残余信号Rf(t)继续进行匹配滤波分解,从而得到Rf(t)的下一阶时频函数表达式和新的残余信号。重复这一过程直到求出各阶残余信号的时频基函数和分解表达式,即:
Rfl(t)=〈Rfl(t),gl(t)〉gl(t)+Rfl+1(t)
l=0,2,…,M-1
(3)
式中,Rfl+1(t)为第l阶改进型匹配滤波得到的残余信号;M为完成匹配滤波分解后得到的所有时频基函数的个数,M≥1。电能质量信号的改进型匹配滤波算法流程如图1所示。

图1 用于电能质量信号分析的改进型匹配滤波算法Fig.1 Improved matched filtering algorithm for power quality signals
图1中f(n)、Rfl(n)分别为离散化的电能质量信号和匹配分解残余信号。于是完成改进型匹配滤波的电能质量连续信号f(t)可以表示为以下函数项和的形式:
(4)
式中,当l=0时的Rfl(t)就是f(t),RfM(t)为含有所有非稳态扰动成分的最终残余信号。
由于在改进型匹配滤波分解过程中使用的正弦时频基函数gγ(t)的支集长度与信号f(t)的时域采样数据窗长相等,即式(1)中的基函数gγ(t)为矩形窗截断的正弦函数,则表达式〈Rfl(t),gl(t)〉gl(t)就是电能质量信号中各稳态谐波成分的正弦时频函数逼近,而最终分解得到的残余信号RfM(t)中就只剩下非稳态扰动成分和噪声。
根据傅里叶变换可知,与时域窗函数等长的正弦时频基函数的频谱是抽样函数频谱Sc(ω)e-jω,其幅值谱固定,通过在相位区间[-π,π]上进行相位扫描、并在频率轴上左右平移基函数频谱就能实现正弦时频基函数的时域平移和调制频率的扫描。因此,在频域中以电能质量信号频谱为对象进行匹配滤波,可降低改进型匹配滤波算法的计算复杂度。分解后得到的时频基函数组合表达式具有形式简洁、逼近效率高且物理意义清晰等优点。
2.2 电能质量信号匹配滤波分析步骤
首先采用正弦时频基函数对谐波等电能质量稳态成分进行匹配滤波,再将得到的时频基函数同被逼近的稳态谐波成分进行比较分析,选用误差最小的区间来估计谐波幅值相位等参数,再从电能质量信号中去除该正弦时频基函数对应的稳态谐波,实现电能质量稳态成分和非稳态扰动成分的分离。
在时域中,电能质量扰动信号一般可表示为:
(5)
式中,fs(t)为包括谐波和间谐波在内的电能质量稳态信号成分;fsl(t)为各次谐波和间谐波;Al、ωl、φl分别为各谐波或间谐波的幅值、角频率和相位;fd(t)为各电能质量信号中的非稳态扰动成分。
利用长度为τ(τ>0)的时域数据窗对电能质量信号进行采样,即:
Wτ(t)=u(t)-u(t-τ)
(6)
式中,u(t)为单位阶跃函数。在时间窗函数支集长度τ足够大的条件下,电能质量信号f(t)中的稳态谐波信号fs(t)与暂态扰动信号fd(t)之间、各谐波信号fsl(t)(l=0, …,M-1)之间彼此正交。所以,采用时频基函数集D中支集长度等于τ的正弦基函数式(7),对各稳态谐波成分的匹配滤波分解效率最高,而且,只需扫描时频基函数gγ(t)的频率ωγ和相位φγ,就能实现稳态谐波的匹配滤波分解和参数估计。
(7)
例如,设gl(t)是对电能质量信号f(t)进行第l次匹配滤波分解得到的正弦时频基函数,即对应于稳态谐波成分fsl(t)有:
αl=〈Rfl(t),gl(t)〉=〈fsl(t),gl(t)〉t∈[0,τ]
(8)
式中,Rfl(t)为经第l-1次匹配滤波分解得到的残余信号,αl为gl(t)在Rfl(t)上的投影系数。fsl(t)和gl(t)可表示为:
fsl(t)=Alsin(ωlt-φl)·Wτ(t)
(9)
(10)
式中,ωEsti_l、φEsti_l分别为电能质量稳态谐波成分fsl(t)的频率ωl、相位φl通过改进型匹配滤波算法得到的估计值。
3 误差分析与准确度提升
3.1 匹配滤波误差分析
在利用匹配滤波算法对电能质量信号进行分析时,谐波幅值估计误差呈现一定变化规律,而且各正弦时频基函数与所对应的稳态谐波间也存在一定的相位估计误差,下面对稳态谐波幅值和相位的匹配滤波误差进行详细讨论。
αl·gl(t)=〈Rfl(t),gl(t)〉·gl(t)
(11)
esl(t)=fsl(t)-αl·gl(t)t∈[0,τ]
(12)
误差函数esl(t)的波形如图2所示。图2中,时域数据窗Wτ(t)的宽度τ=1.0 s且谐波成分fsl(t)幅值为1.0 V。由图2可见,误差函数esl(t)的大小呈近似线性变化;在时间窗中点(t=0.5 s)处及附近误差最小,而在时间窗两端误差最大;可见在时域数据窗中点附近,谐波信号fsl(t)与匹配滤波表达式αl·gl(t)拟合得最好,幅值和相位估计得最准确。因此,可利用时间窗中点附近这一小段时间(如整个窗函数长度的1/10)内的匹配表达式αl·gl(t)来估计谐波fsl(t)的幅值和相位,这样得到的参数估计误差比时间窗两端处误差小一个数量级,因此,可以采用滑动窗的方法在时间窗中点附近实现电能质量信号分析来获得较高的分析精度。
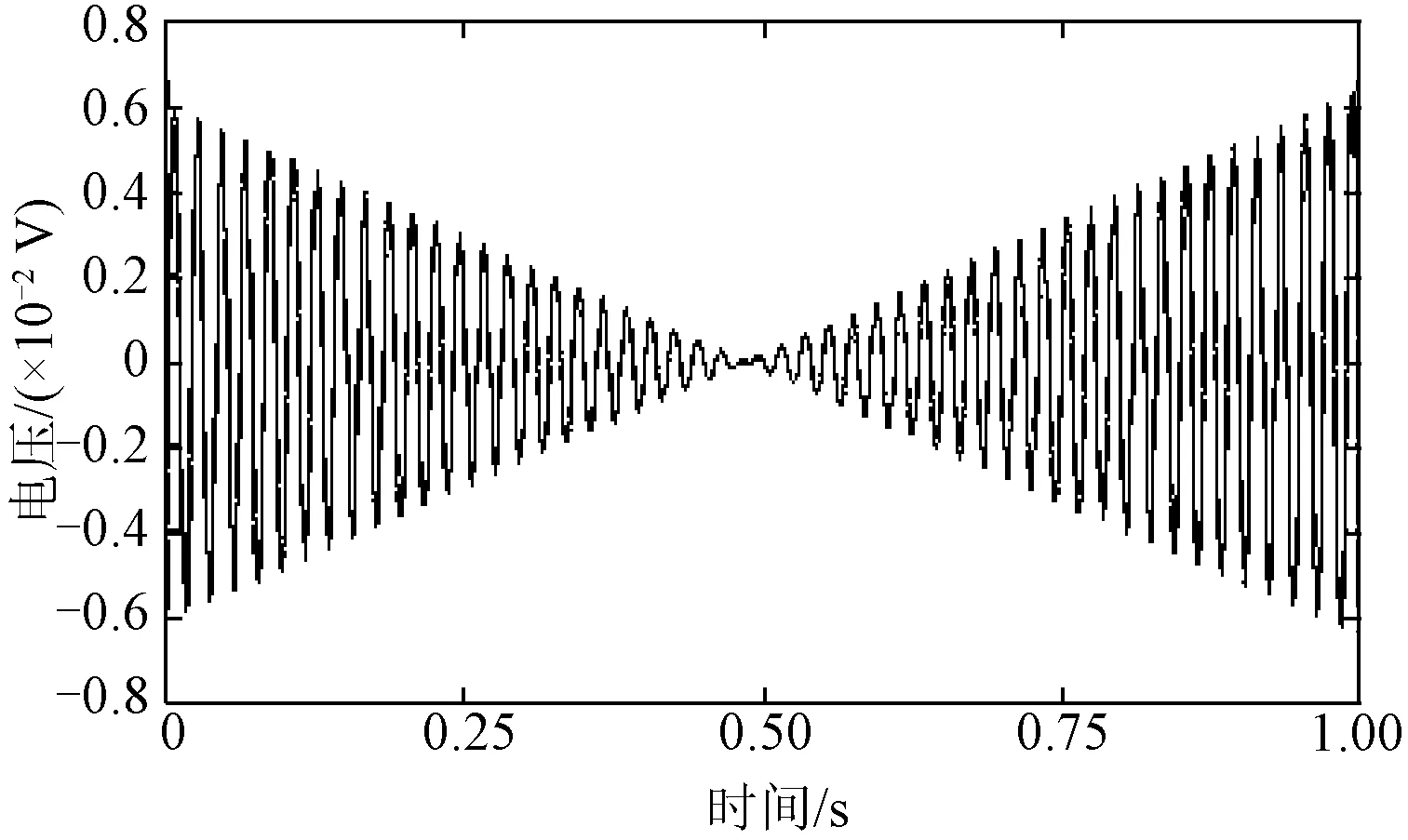
图2 第l次谐波匹配滤波误差函数esl(t)Fig.2 Error function esl(t) of lth harmonic by matched filter
3.2 改进型匹配滤波误差最小区间
设匹配滤波分析采用的时域数据窗Wτ(t)为宽度1.0 s的矩形窗,式(10)所示第l次谐波的频率、相位估计值可表示为:
ωEsti_l=ωl+Δωl
(13)
φEsti_l=φl+Δφl
(14)
式中,Δωl、Δφl分别为谐波频率及相位的估计偏差。
根据式(8)及谐波fsl(t)与残余信号Rfl(t)中各扰动成分的正交性,并将式(13)、式(14)代入式(15)中可知,该次谐波匹配滤波的内积投影系数计算如下所示:
(15)
利用三角函数积化和差得:
(16)
由于式(16)中的第二个积分项中余弦函数频率是稳态谐波fsl(t)的二倍频,其在时间区间[0,τ]上的积分趋近于零。则内积αl可近似为:
(17)
和差化积可得:
(18)
当式(18)中余弦函数项为1,即其相角如下:
(19)
第l次谐波的内积αl取得最大值,即获得该次谐波匹配滤波的投影系数。
当稳态谐波fsl(t)信号在区间[0,τ]上进行匹配滤波时,算法内积最大化将要求频率偏差Δωl位于(-2π/τ,2π/τ)范围之内,则式(19)所示相位偏差的范围为:
(20)
即当匹配追踪相位偏差Δφl=Δωlτ/2时,改进型匹配滤波系数αl=〈Rfl(t),gl(t)〉 取得最大值。
(21)
将式(13)、式(14)、式(20)所确定的频率和相角关系代入式(9)和式(10),且分析的时间点取时间窗中点t=τ/2,可得:
(22)
(23)
式中,fsl(t)为各稳态谐波和间谐波成分。由式(22)、式(23)可知,fsl(t)和gl(t)在时间窗Wτ(t)的中点处具有相同的相位,即相位最佳逼近。
由于稳态谐波频率估计误差Δωl一般都很小,则式(21)内积可近似等于:
(24)
则l次谐波的改进型匹配滤波分析表达式为:
(25)
该匹配滤波表达式在时间窗Wτ(t)中点附近与稳态谐波fsl(t)非常相似,波形关系如图3所示。

图3 时间窗中点相位最佳逼近Fig.3 Phase best approximation at midpoint of data window in time-domain
由图3可见,第l次谐波的改进型匹配滤波表达式αl·gl(t)能够很好地逼近稳态谐波fsl(t)的波形。
对电能质量信号中的各次稳态谐波都进行匹配滤波分析和参数估计,然后分离这些谐波成分,得到的残余信号RfM(t)中将只含有电能质量非稳态扰动成分,可供后续进一步分析处理。
3.3 基于滑动窗的匹配滤波性能提升
本文采用滑动时间窗的方法,在时间窗中点附近区间实现电能质量信号的匹配滤波分析,提高谐波参数估计和非稳态扰动成分分离的准确度。
不失一般性,设时间窗Wτ(t)长度τ=1.0 s且滑动步长为Δ=τ/10=0.1 s,如图4所示。

(26)

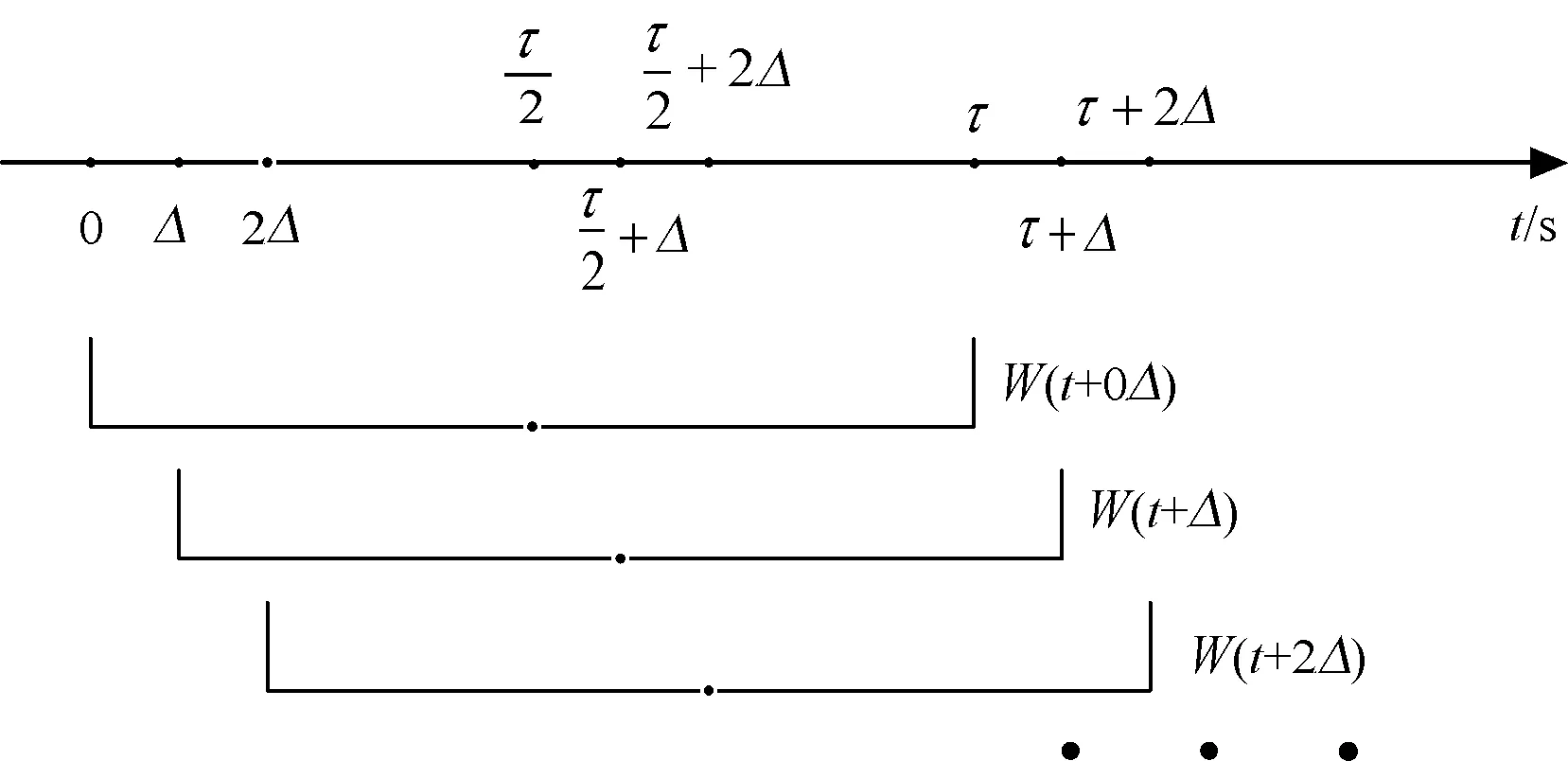
图4 滑动时间窗匹配滤波Fig.4 Sliding windows for matching filter in time-domain
可见,在时间窗中点附近,改进型匹配滤波算法能够很好地逼近稳态谐波,从而准确估计谐波参数并将非稳态扰动成分与电能质量信号中的谐波等稳态成分比较彻底地分开。
4 应用算例
4.1 算例生成及谐波分析
本算例研究的对象是含稳态谐波和间谐波以及非稳态扰动的电能质量信号,信号组成如下所示:
(27)
各成分频率、幅值、相位参数见表1。

表1 电能质量信号稳态成分参数Tab.1 Parameters of power quality stable components
含有这些谐波及间谐波成分的电能质量信号波形如图5(a)所示。
在本例中,除了谐波和间谐波,电能质量信号中还含有非稳态扰动成分fd(t),其波形如图5(b)所示,包括暂态振荡(信号1、信号2和信号13)、衰减暂态振荡(信号3、信号4)、脉冲(信号5、信号6)、基波幅值骤变(信号7、信号9、信号10、信号11和信号14)、电压切痕(信号8)以及暂态振荡与基波幅值骤变的叠加(多重扰动,即信号12)。由图5(a)可见,由于基波和稳态谐波的存在,这些幅值较小的非稳态扰动成分几乎无法察觉,也难以开展进一步的分析。

为了比较常规匹配滤波与改进型匹配滤波方法的性能优劣,首先采用这两种方法分别对电能质量信号中的稳态谐波进行分析,估计各次谐波的频率、幅值和相位参数,计算估计误差,比较两种分析方法的准确度。其中,匹配滤波相位扫描步长为0.1°,频谱扫描步长为1/256 Hz,稳态谐波(包括间谐波)参数估计误差见表2、表3。

表2 电能质量信号稳态成分参数常规匹配滤波估计误差Tab.2 Estimation error of steady-state component parameters of power quality signals by conventional matching filter

表3 电能质量信号稳态成分参数改进型匹配滤波估计误差Tab.3 Estimation error of steady-state component parameters of power quality signals by improved matching filter
对比表2、表3中稳态谐波成分参数估计误差可知,与常规方法相比,改进型匹配滤波方法对稳态谐波的频率、幅值估计误差减小了一半,相位估计准确度提高了一个数量级,显著提高了谐波和间谐波等电能质量稳态成分分析的准确度,特别是为稳态成分和非稳态扰动成分的准确分离提供了条件。
4.2 采用改进型匹配滤波算法分离非稳态扰动
对于式(27)所示电能质量信号f(t),采用常规和改进型匹配滤波算法对所有稳态谐波成分进行参数估计和波形分离,分离后得到的非稳态扰动成分fd(t)的波形如图6所示。

比较图6(a)和图6(b)可以看到,利用改进型匹配滤波算法较精确地分离了电能质量信号中非稳态扰动成分,即便是幅值很小很微弱的切痕信号8(幅值为0.3 V)也被很好地分离出来。可见,改进型匹配滤波方法将电能质量信号中的非稳态扰动完整地提取出来。而且,对于时间支集重叠的非稳态扰动,如多重扰动12(幅值骤变+暂态振荡),改进型匹配滤波算法也能将其可靠地分离出来,便于后续进一步地分析识别和参数估计。
为了进一步验证基于改进型匹配滤波的非稳态电能质量信号分析方法的抗干扰能力,在式(27)所示电能质量信号中加入方差σ2=0.1的白噪声。取一段长度为1.0 s的含非稳态扰动成分的电能质量信号,分别采用常规匹配滤波和改进型匹配滤波方法分离其中的稳态谐波成分,得到的电能质量信号非稳态扰动成分波形如图7所示。

从图7(b)可以看出,在存在背景白噪声时,改进型匹配滤波算法仍能较彻底地分离电能质量信号中的稳态谐波和非稳态扰动成分,便于后续对非稳态扰动成分的进一步分析;而图7(a)所示波形则存在着较大的稳态谐波残余成分,很难对其进行非稳态扰动成分的支集划分、分析分类以及参数估计等处理。
改进型匹配滤波算法不仅能够实现电能质量稳态谐波与非稳态扰动的可靠分离,而且对稳态谐波相位的估计准确度较高。例如,对于表1中的7次谐波,利用改进型匹配滤波算法和常规匹配滤波算法分析该次谐波相位,所得相位误差曲线对比如图8所示。

图8 谐波相位估计误差比较Fig.8 Harmonic phase estimation error comparison
图8中,曲线1是7次谐波常规匹配滤波算法得到的相位估计误差(约1°),曲线2是基于改进型匹配滤波算法得到的相位估计误差(约0.1°~0.2°),改进型匹配滤波算法对谐波相位的估计准确度提高了一个数量级。将常规匹配滤波和改进型匹配滤波算法得到的电能质量信号各次稳态谐波相位误差进行对比,具体见表4。

表4 电能质量信号稳态谐波相位估计误差Tab.4 Steady-state harmonic phase estimations errors of power quality signals using conventional and improved matching analysis methods
由表4可知,改进型匹配滤波算法的抗白噪声干扰能力很强,对电能质量信号稳态谐波相位的估计准确,对非稳态扰动成分的分离提取完整。
综合以上算例结果可知,电能质量信号匹配滤波分析方法在时间窗中点附近能较好地逼近稳态谐波,但是离开中点越远则逼近误差越大,影响谐波参数估计准确度和稳态分量与非稳态扰动分量的分离效果。该误差主要影响稳态谐波相位估计的准确度,即在中点附近长度为时间窗支集十分之一区间内的相位估计误差比窗两端处的误差小一个数量级,因此采用时间窗中点所在小区间内的相位作为稳态谐波相位的估计值,能够获得较高的相位估计准确度。
此外,该误差还影响稳态分量与非稳态扰动分量的分离效果。当得到一个正弦稳态分量幅值和频率的估计值后,可直接得到该稳态分量的正弦估计波形,稳态分量和估计波形在时间窗端点处因相位误差大而使波形差别很大,如图3波形相位关系所示,因此利用该正弦估计波形实现的稳态分量和非稳态扰动分量的分离误差也比较大(如图6(a)所示),图6中分离得到的非稳态扰动分量波形很难进行分割、识别和参数估计;与之不同,稳态分量同其正弦估计波形在相位误差较小的时间窗中点附近彼此很接近,因此在时间窗中点附近区间内分离各稳态分量,得到的非稳态扰动分量波形畸变小、分离效果较好(如图6(b)所示),便于非稳态扰动分量的后续分析处理。
5 结论
针对现代电力系统内非稳态电能质量扰动成分难以准确提取的问题,本文提出了一种基于改进型匹配滤波的非稳态电能质量信号分析方法。该方法通过正弦时频基函数集不断逼近电能质量信号中的各稳态谐波成分,经分离后得到完整的非稳态扰动成分和噪声。在实现电能质量信号稳态谐波匹配滤波分解和参数估计的过程中,发现了谐波参数估计误差具有时间窗中点附近最小化的规律,并利用这个规律有效降低了稳态谐波相位的估计误差。经算例验证,利用改进型匹配滤波算法能够实现稳态谐波参数的准确估计和非稳态扰动成分的精确分离,提高了非稳态电能质量扰动成分分析的准确度。该方法为电力电子化电力系统的电能质量分析与治理提供了有效手段。
需要指出,本文提出的基于改进型匹配滤波分析方法适用于噪声背景下非稳态电能质量信号扰动成分的分析分离。但是,由于该算法采用了时域滑动窗的方法来提高分析结果的准确度,增加了算法的计算量,降低了实时性,因此在后续研究中需要提出简化计算的快速算法,来提高非稳态电能质量信号分析的实时性和准确度。

