基于Markov状态空间法的稳控系统隐性故障建模方法

蒋 航， 熊 俊， 陈 愚， 陈柏汗， 封 科， 刘 平， 欧阳金鑫

(1. 国家电网有限公司西南分部， 四川 成都 610094； 2. 国电南瑞科技股份有限公司电网安全稳定控制技术分公司， 江苏 南京 211106； 3. 输配电装备及系统安全与新技术国家重点实验室(重庆大学)， 重庆 400044)

1 引言

安全稳定控制装置(稳控装置)装设在厂站内，是扰动时保证电力系统正常运行的控制设备，多个厂站的稳控装置经通信设备联络构成的系统称为安全稳定控制系统(稳控系统)。稳控系统是电力系统的第二道、第三道防线，可实现电力系统的振荡解列、低频减载、低压减载等功能[1]。

稳控系统的隐性故障指状态维修手段不能检测出的、在电力系统发生短路等故障时，直接引起稳控系统误动、拒动或控制措施不当的一种功能性缺陷[2]。隐性故障的存在可能导致稳控系统将电气元件错误或不适当地从系统中移除，造成电力系统事故的进一步扩大。近几年，由稳控系统隐性故障导致的电力系统停电事故更是不在少数[3]。对稳控系统的隐性故障进行分析与建模，从而实现隐性故障预测与诊断是排除稳控系统隐性故障、提高稳控系统运行可靠性的有效措施。

现有隐性故障建模主要从可靠性评估角度对系统隐性故障失效风险进行分析。文献[3]对比了马尔可夫状态空间法、事件树分析法和故障树分析法三种可靠性分析方法的优劣，证明了可靠性分析在隐性故障建模中的优势。文献[4]从概率、网络结构、能量损失三个角度建立输电系统隐性故障评估指标，建立了隐性故障模型。文献[5]将电力系统隐性故障分为五类,并利用马尔可夫状态空间法从五类风险指标评估电力系统隐性故障。文献[6]用最小割集分析法进行变电站通信系统隐性故障定性分析,并利用故障树分析法进行了可靠性评估。文献[7]基于潮流相关性进行电网线路隐性故障分析，根据二级连锁故障发生时有功潮流的转移特征构建电力系统隐性故障评估指标。但是，电力系统隐性故障的分析与建模主要关注于一次设备。

目前部分研究关注了继保系统的隐性故障，文献[8]建立了继电保护系统的隐性故障概率模型，文献[9]从风险评估角度分析了隐性故障的影响，并运用可靠性分析方法对继保系统隐性故障进行了分析。但是，由于稳控系统与继电保护系统在组成元件、运行原理、功能等的区别，且稳控系统存在分布式、多运行模块的特点，因此继保系统的隐性故障分析方法无法适用于稳控系统。文献[10]梳理了稳控系统各环节可能存在的隐性故障，但缺乏对稳控系统隐性故障的量化分析。

Markov状态空间法利用概率指标量化稳控系统隐性故障状态，可以有效描述稳控系统多分布结构下各环节隐性故障失效过程。文献[11,12]指出Markov状态空间法能将电力系统隐性故障按环节划分并细化至装置本体，能有效反映隐性故障的特征。为此，本文采用Markov状态空间法对稳控系统的隐性故障进行建模评估。考虑了稳控系统存在隐性故障的各个环节，提出了基于Markov状态空间法的稳控系统隐性故障建模方法，实现了稳控系统的隐性故障状态评估，为稳控系统的可靠性分析提供了依据。

2 稳控系统隐性故障环节

2.1 稳控系统隐性故障分析

稳控系统故障类型有一类失效与二类失效[13]。稳控装置故障导致稳控系统失效被称为一类失效，包括一类拒动与一类误动。电网发生故障时，稳控系统功能失效被称为二类失效，包括二类拒动与二类误动。一类误动是显性故障，一类拒动、二类拒动只有在电网故障或潮流波动，需要稳控系统动作时才会触发，稳控系统的二类误动也只有电网运行状况发生变化才能触发[4]。因此，稳控系统的隐性故障指的是稳控系统拒动与非选择性误动(二类误动)。

稳控系统常配置有自检功能，稳控装置运行过程中，若某元器件失效并被检测到，则稳控系统进入停运状态，直至该故障被修复后才重新投入运行；若某个元器件失效而未被检测到，则稳控系统进入隐性故障状态(隐性拒动状态或隐性误动状态)；若稳控系统处于隐性故障状态，电网发生故障，稳控系统拒动或误动，稳控系统进入故障状态。

2.2 稳控系统隐性故障环节

稳控系统功能是基于装置分散控制、分布信息完成的。隐性故障的分布呈现分散式，在稳控系统的各个环节均有可能出现。稳控系统运行环节大致分为策略、表决模式、通信、测量、定值、软件和人工7个环节。

稳控装置的跳闸判据是实施稳控系统控制策略的基础，测量环节所得信号量与定值环节设置量进行比较，构成是否跳闸的判据。在进行可靠性分析中，控制策略环节导致稳控系统处于隐性故障的风险，往往可通过定值与测量环节反映。稳控系统的表决模式利用冗余设计法来提高稳控系统的安全性，可有效防止单套装置隐性故障而造成的拒动和误动。表决模式环节不会造成稳控系统的拒动或误动。因此，稳控系统隐性故障概率模型可不考虑策略环节与表决模式。因此，稳控装置的隐性故障建模主要考虑以下5个环节。

通信：通信环节可能存在误码率过高、通信通道衰耗过大等问题，严重时可能导致通信环节失效，影响命令的接收和执行[8]。

测量：电气元件的模拟电气量通过电子式电流互感器、电子式电压互感器，经由CPU处理后转换成数字量。测量环节出错可能造成故障误判导致装置误动作。

定值：装置的定值正确与否决定着装置能否有效发挥作用。

软件：稳控系统软件随运行时间的增加可能会产生运算错误、软件失能等问题。软件环节的可靠性对稳控系统正常运行有重要作用。

人工：运行、检修人员的误操作可能导致稳控系统处于隐性故障状态。

3 稳控系统隐性故障评估方法

隐性故障的存在将导致稳控系统在某些情况下拒动或误动，影响稳控系统的可靠运行，主要体现在故障率、失效率等可靠性指标。Markov状态空间法是一种通过状态转移图描述系统故障状态的可靠性分析技术[3]。Markov法将系统拆分细化为各个环节，各个环节分为故障状态或正常状态，各个环节的状态组合，构成整个系统的状态。当某环节出现故障或故障修复后，该环节状态发生变化，整个系统也将从某一状态转移到下一状态，系统的不同状态之间通过一定的概率相互转换，从而可构建出稳控系统的状态转移图，即Markov状态空间模型。通过对状态空间模型进行数学分析，即可求得稳控系统处于不同状态的平稳状态概率，并进一步确定稳控系统的综合误动率、综合拒动率、可用度等可靠性指标，实现稳控系统隐性故障的可靠性评估，具体流程如图1所示。

图1 稳控系统隐性故障建模及评估方法Fig.1 Hidden fault modeling and evaluation method for stability control system

4 稳控系统隐性故障评估指标

稳控系统可靠性分析中，关键技术指标有可用度、故障率、平均寿命、系统失效度等。可用度是对稳控系统可靠性评估的总体参数；故障率是对稳控系统进行隐性故障分析时的核心参数，需要对各环节分别求取故障率；平均寿命与稳控系统修复率相关；系统失效度反映稳控系统失效概率，为综合误动率与综合拒动率之和。

可用度A是表征稳控系统在任意时刻处于正常状态的概率[9]，其计算式为：

A=P0

(1)

式中，P0为稳控系统处于正常状态的平稳状态概率。

故障率为单位时间内失效的元件数与元件总数之比，定义式为：

(2)

式中，λw为元件误动故障率；λj为元件拒动故障率；Tw和Tj分别为稳控系统的无故障(即未发生误动或拒动)工作时间；P(tt)为元件在无故障工作时间t后，在t+Δt时间段内误动的条件概率；P(tt)为元件在无故障工作时间t后，在t+Δt时间段内拒动的条件概率。

稳控系统的隐性故障可能导致稳控系统出现两种故障模式：拒动和误动。稳控系统拒动与误动导致的系统后果也不一样，在建模时需要分别考虑，在求解故障率的基础上进一步求解拒动率与误动率。从长期运行数据来看，由稳控系统隐性故障导致的稳控系统拒动或误动次数相差不大[3]。则稳控系统各环节的误动故障率和拒动故障率分别为该环节各个稳控装置故障率之和的一半。

通信环节可能存在误码率过高，通信通道衰耗过大等问题，影响命令的接收和执行，通信环节可能出现故障的装置有：集线器、交换机、路由器、智能电子设备(Intelligent Electronic Device, IED)、网络接口设备和服务器等硬件设备[6]。故障率则可写为：

λt=λh+λswi+λrouter+λI+λser

(3)

式中，λh为集线器故障率；λswi为交换机故障率；λrouter为路由器故障率；λI为IED网络接口设备故障率；λser为服务器故障率。

测量环节包括采样处理单元和信息处理单元。以SCS-600数字式稳控装置为例，合并单元负责发送处理过的采样值报文，经接收后由信息处理单元进行电气量运算等处理。电气量运算功能集成在SCS-600数字式稳控装置的现场可编程门阵列(Field Programmable Gate Array, FPGA)内部[13]。可能出现故障的硬件模块有：信息处理单元模块、合并单元[11]。因此，测量环节故障率为：

λc=λGOOSE+λhb

(4)

式中，λGOOSE为通用面向对象变电站事件(Generic Object Oriented Substation Event，GOOSE)模块故障率；λhb为合并单元故障率。

定值环节可能出现的故障为：开关控制器逻辑节点、隔离开关逻辑节点和断路器逻辑节点判断错误[12]，这些模块出现故障将直接导致稳控装置误动或拒动[13]，另外由于动作定值设置不当可能导致稳控装置拒动与非选择性误动[14]。

误动率为：

(5)

拒动率为：

(6)

由于动作定值设置不当造成稳控系统误动的误动率为：

(7)

由于动作定值设置不当造成稳控系统拒动的拒动率为：

(8)

对于测量、通信、定值环节的稳控装置硬件部分，其具体设备的故障率是在一个统计周期内，对电网中同电压等级的多个稳控系统进行统计得到的。计算如下所示：

(9)

式中，λ为测量、通信、定值环节各硬件模块的故障率；N为统计期间硬件发生故障的次数。

稳控系统软件环节的故障多为软件逻辑设计的错误，例如，对于数据的需求分析不准确，额定值数的输入与程序设计冲突，数据编码存在逻辑上错误等。软件缺陷是由于在需求分析、设计或程序编写等阶段中引入的，其一旦生成则将长期潜伏在软件中直到排除为止，并随时都有导致软件故障的可能。考虑到软件运行时间与故障率的关系，选取Logarithmic exponential 模型求解稳控系统的软件故障率，可得：

(10)

误动率为：

(11)

拒动率为：

(12)

式中，λ0为初始故障率；T0为初始故障运行时间；M0为软件缺陷数；τ为截止到进行故障率计算时程序已经运行的时间；τ′为程序从进行故障率计算时开始，程序还可再运行的时间[15]。

运行、检修人员的误操作也是导致稳控系统产生隐性故障的重要原因。大部分人工操作故障率分析都从人员操作手册中选取通用数据进行分析，对于稳控系统中人工操作失误的隐患，需要拟合操作人员行为模式与完成任务过程。因此采用两参数威布尔分布拟合法进行定量计算[16]，其故障率为：

(13)

式中，t为操作人员对所下达操作任务的响应时间；T0.5为执行人员完成某项任务所用的中值时间；η、β分别为认知行为模型的尺度、形状因数，可通过手册查阅。

故障率指标获取来源有：装置实际运行经验数据统计、装置历史运行数据库、装置实际寿命测试、可靠性数据的标准手册[17]。因此，可以通过各种维修统计、检测报告、装置正确动作的统计、装置拒动和误动的统计计算稳控装置的故障率。

对于稳控装置，故障发生后短时间内有可能完成故障修复，使稳控系统能及时地恢复正常工作，因此稳控装置在故障过程中存在一个修复率。不同环节对应的修复率不同，而同一环节的误动故障与拒动故障的修复率也不同。修复率可从稳控系统各装置的历史运行数据中统计得到[18]。

5 稳控系统隐性故障建模

采用Markov状态空间法对稳控系统进行隐性故障建模时，考虑工程实际要求，做出如下假设：稳控系统各部分的故障率和修复率为常数；稳控装置具有自检功能，能通过装置自检功能发现并成功修复故障的概率为自检系数；稳控装置软件失效、硬件失效及人员失误相互独立[19]；不考虑一次系统处于故障状态时的情况，仅考虑稳控系统处于隐性故障的可能性，即一次系统处于正常工作状态；在稳控系统进入误动或拒动状态后，对整个系统进行检修，不引入新的故障，直至故障被修复，即进入正常状态后，才可能再发生故障。

5.1 稳控系统状态空间模型

稳控系统的Markov状态空间图如图2所示。

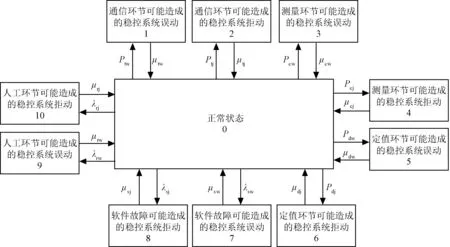
图2 稳控系统的状态空间图Fig.2 State space diagram of stability control system

对于通信环节、测量环节、定值环节具有自检功能的硬件设备，当故障发生时，若没有及时自检发现并消除故障，则整个稳控系统转化为误动或拒动状态。稳控系统由正常状态转化为误动状态的概率为：

Piw=(1-Ci)λiw

(14)

式中，i为不同环节，可为t、c、d，分别对应于通信环节、测量环节、定值环节；Piw分别对应为Ptw、Pcw、Pdw，分别为通信环节、测量环节、定值环节从正常状态转化为误动状态的概率；Ci分别对应为Ct、Cc、Cd，分别为通信环节、测量环节、定值环节对应的自检系数；λiw分别对应为λtw、λcw、λdw，分别为通信环节、测量环节、定值环节对应的误动率。

稳控系统由正常状态转化为拒动状态的概率为：

Pij=(1-Ci)λij

(15)

式中，Ptj、Pcj、Pdj分别为通信环节、测量环节、定值环节从正常状态转化为拒动状态的概率；λtj、λcj、λdj分别为通信环节、测量环节、定值环节对应的拒动率。

对于软件环节与人工环节，故障发生后无自检，因此转化为误动状态的概率分别为λsw和λrw，转化为拒动状态的概率分别为λsj和λrj。当故障被修复后，稳控系统才恢复到正常工作状态。系统从误动状态恢复到正常工作状态的概率分别为μsw和μrw，系统从拒动状态恢复到正常工作状态的概率分别为μsj和μrj。μtw、μcw、μdw分别为通信环节、测量环节、定值环节的误动故障修复率，μtj、μcj、μdj分别为通信环节、测量环节、定值环节的拒动故障修复率。

基于状态空间图，可求出稳控系统在各个状态的平稳状态概率及系统的平稳状态概率矩阵P：

P=[P0P1P2P3P4P5P6P7P8P9P10]

(16)

稳控系统的状态转移矩阵为：

(17)

式中

(18)

根据Markov状态空间理论，可得：

(19)

可求得系统处于正常状态的平稳状态概率为：

(20)

系统处于由通信环节、测量环节、定值环节故障造成系统误动状态的平稳状态概率分别为：

(21)

系统处于由通信环节、测量环节、定值环节故障造成系统拒动状态的平稳状态概率分别为：

(22)

式中，p=1,2,3，分别对应于i为t、c、d，即稳控系统通信环节、测量环节、定值环节故障。

系统处于由软件环节、人工环节故障造成系统误动状态的平稳状态概率分别为：

(23)

系统处于由软件环节、人工环节故障造成系统拒动状态的平稳状态概率分别为：

(24)

式(23)、式(24)中，p=4，5，分别对应于i为s、r，即稳控系统软件环节、人工环节故障。平稳状态概率P2p-1、P2p分别对应于平稳状态概率矩阵中的概率值。

5.2 稳控系统隐性故障概率

稳控系统隐性故障概率指当前稳控系统运行于隐性故障状态的概率，为不同环节导致的稳控系统处于隐性故障状态的概率之和，是状态平稳矩阵中所有非正常运行状态概率值之和[20]。根据稳控系统状态空间图，可量化稳控系统发生拒动或误动事件的概率。当稳控系统因某环节故障而处于隐性故障状态时，稳控系统运行存在风险，隐性故障概率是对稳控系统运行风险的一种量化评估。

系统的综合误动率为系统从正常状态转移到误动状态的概率之和为：

PW=P1+P3+P5+P7+P9

(25)

系统的综合拒动率为系统从正常状态转移到拒动状态的概率之和为：

PJ=P2+P4+P6+P8+P10

(26)

因此，稳控系统的隐性故障概率为PW+PJ。

6 算例分析

以某220 kV稳控系统为例，根据电网的历史可靠性数据，并参考标准手册，采集稳控系统测量环节、通信环节、定值环节在一个统计周期内硬件故障的次数，采集软件环节的无故障运行时间，采集人工环节中执行人员完成某项任务所用的中值时间。统计测量环节、通信环节、定值环节的自检系数，可得通信环节失效自检系数为0.875，测量环节失效自检系数为0.9，定值环节失效自检系数为0.8。统计各环节故障修复率见表1，其中，μw为各环节误动故障修复率，μj为各环节拒动故障修复率。

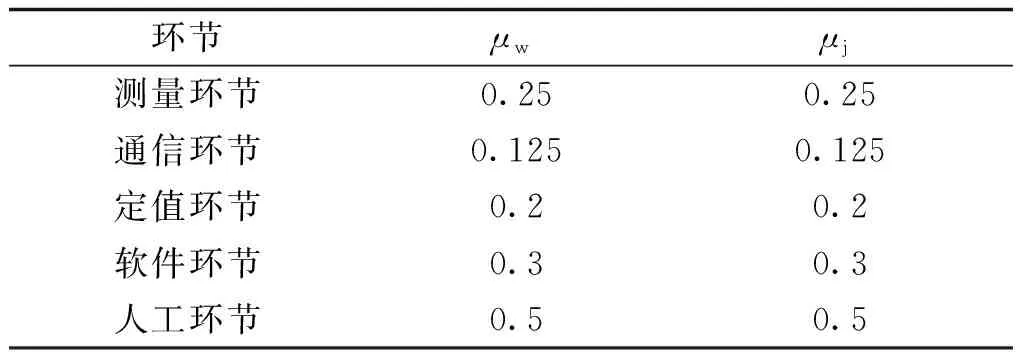
表1 稳控系统各环节修复率参数Tab.1 Repair rate parameters of each link of stability control system (单位：h-1)

人工环节可靠性参数为：

η=1.421 7

β=1.741 5

通过拟合法计算人工操作故障率：

λr=2.824×10-4h-1

λrw=λrj=1.412×10-4h-1

软件环节的可靠性参数为：

λ0=5.714×10-4h-1

τ′=7 962.63 h

τ=63 712 h

求得软件环节的失效率为：

λs=5.043×10-4h-1

λsw=λsj=2.522×10-4h-1

基于采集数据和各环节故障修复率数据，对测量环节、通信环节、定值环节故障率进行计算。汇总各环节的故障率计算结果见表2，其中λ为各环节整体故障率。由表2可知，稳控系统各环节故障率参数数量级为10-4，发生故障的概率较小，可知该系统长期运行在正常状态下。

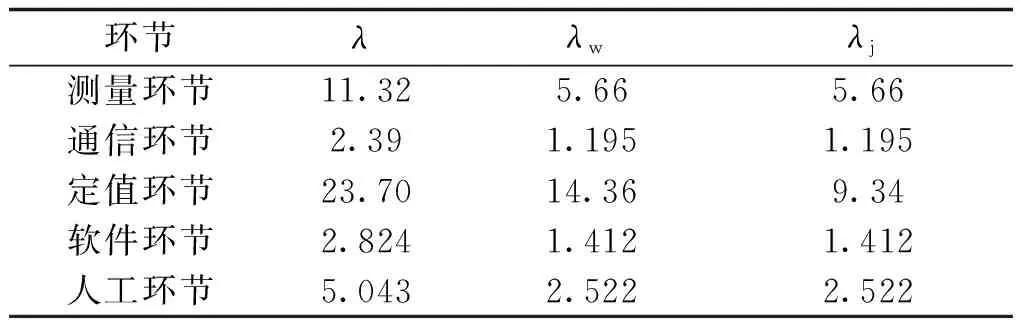
表2 稳控系统各环节故障率参数Tab.2 Failure rate parameters of each link of stability control system (单位：10-4 h-1)

将各环节故障率代入状态转移矩阵中，可求得稳控系统处于不同状态的平稳状态概率见表3。由表3可知，由于定值环节失效导致稳控系统处于隐性故障状态的概率最大。人工环节导致稳控系统处于隐性故障状态的概率较小，这表明当前稳控系统的自动化、智能化程度不断提高，人为因素影响较小[21]。

表3 稳控系统平稳状态概率Tab.3 Probability of steady state of stability control system

由表3的结果可知，稳控系统不同状态的平稳状态概率表现了稳控系统当前的运行状况，系统处于正常运行状态的概率约为99.42%，处于因测量环节失效导致的系统隐性故障状态的概率约为0.005%，可以判断当前系统很大可能处于正常工作状态。

基于稳控系统各状态的平稳状态概率，可计算稳控系统的综合误动率PW和综合拒动率PJ见表4。由表4可知，稳控系统的可用度很高，这与稳控系统运行统计数据结果一致[22]。

表4 稳控系统隐性故障概率计算结果Tab.4 Calculation results of hidden failure probability of stability control system

由表4计算结果可知，稳控系统处于隐性误动状态的概率比处于隐性拒动的概率要高一些，主要原因是稳控系统处于隐性误动状态比处于隐性拒动状态更容易被触发，在稳控系统实际运行中更容易被统计到。稳控系统处于综合误动状态的概率为0.315%，处于综合拒动状态的概率为0.265%，表明当前稳控系统可靠性较高，存在隐性故障的可能比较小。这与在线自检等提高系统可靠性的措施在稳控系统中的运用是分不开的[23]。

7 结论

稳控系统是保障电力系统安全稳定运行的重要防线，针对鲜有研究关注稳控系统隐性故障建模评估方面的问题，本文首先梳理了稳控系统隐性故障的可能环节，建立稳控系统隐性故障的评估指标体系，且进一步建立基于Markov状态空间法的稳控系统隐性故障概率模型。该模型能对稳控系统隐性故障状态进行量化分析，并对系统各个环节可能出现隐性故障的概率进行求解，可用于稳控系统隐性故障的评估，对保障电网稳控系统的正常运行具有重要意义。