高速角接触球轴承中的冲击滑动研究*

张 涛 赵利锋 顾家铭

(1.上海集优机械有限公司轴承技术中心 上海 201108；2.上海天安轴承有限公司 上海 201108)

在航空发动机主轴、涡轮起动机等的转子系统中，对关键支撑部件滚动轴承的转速和寿命要求越来越高。高速轴承中滚动体打滑是影响轴承动态性能和工作寿命的重要因素之一。在高速轻载、联合载荷及时变工况下的轴承中经常出现滚动体打滑。打滑会导致摩擦发热和磨损，发热使轴承及润滑油温度剧增，局部高温破坏润滑油膜，油膜破裂导致磨损加剧，从而导致轴承旋转精度降低，诱发振动噪声，使轴承在早于疲劳剥落前失效[1]。球轴承中球与滚道的滑动包括陀螺滑动、自旋滑动、差动滑动(局部)及拖动滑动(整体)，而通常所说的轴承打滑是指由于滚动体滑动速度分量增大导致其滚动速度低于理论值，一般利用滚动体或保持架的打滑率来表示轴承打滑程度[2-3]。轴承实际运转中往往同时存在几种滑动模式，高速工况下由于离心力和陀螺力矩明显增大，使球的运动更为复杂。

随着滚动轴承力学分析模型的发展，高速球轴承的打滑问题研究不断深入。JONES[4]以轴承拟静力学模型为基础，基于套圈控制假设，研究了推力载荷下球的接触角、载荷和力矩以及球的滚动轴线方向等性能参数，并定义了球轴承不发生陀螺滑动的推力载荷阈值。随后，HARRIS[5]和WALTERS[6]采用简化的弹性流体动力牵引模型，对Jones理论模型进行修正使之更接近实际工况，并通过解析方法分析滚动体的打滑率。BONESS[7]通过对不同工况的计算机模拟，建立了轴承系统最小载荷要求的通用表达式。当所施加的轴承载荷不足以在滚道和滚动体之间产生足够的弹性流体动力牵引力，以克服保持架阻力、搅动损失并防止陀螺旋转时，就会发生打滑。

以上分析方法都是基于常规的准静态力平衡方法，只适用于推力载荷下陀螺打滑和拖动打滑分析。然而，在联合载荷及时变工况下，球在转动过程中接触角、载荷及角速度动态变化，球的打滑具有时变性，这时就要以动力学模型为基础进行研究。GUPTA[8-9]建立了轴承各零件具有6个自由度的广义运动微分方程，通过数值积分可以获得零件的瞬态运动特性。这些方程可以与任意牵引-滑动模型和初始条件集成，可以预测给定工况和润滑剂牵引曲线下球的各种滑动和磨损率，从而建立打滑引起的磨损与施加的载荷之间的关系，由此可以确定防止轴承打滑所需要的预紧力。但是GUPTA的动力学模型过于复杂，不便于工程应用。JAIN、HUNT[3,10]提出了一个简化动力学模型，考虑了陀螺力矩、离心效应及弹流润滑牵引性能的影响；分别研究了角接触球轴承在纯轴向载荷、轴向径向联合载荷及变速工况下滚动体的打滑机制，讨论了纯轴向载荷下的陀螺滑动和拖动滑动，联合载荷下滚动体进入和离开径向载荷区的瞬时滑动，以及变速工况下的整体滑动；通过公式推导给出了不同工况下轴承打滑临界载荷的计算公式。尽管公式推导中做了许多假设，但其系统的研究也获得了一些有益的结果，为工程应用提供了有价值的参考。

国内早期主要基于拟动力学方法研究航空高速球轴承的打滑[11-12]，并根据滚动体和保持架的打滑率确定临界预紧载荷。近年来，随着滚动轴承动力学模型的发展，对滚动体的瞬态打滑特性研究也取得了重要进展。涂文兵等[1,13]建立了滚动体变载荷和变转速工况下的打滑动力学模型，研究了滚动体进入和离开承载区时的打滑和瞬态运动行为，其动力学模型中各零件仅限于轴承径向平面内运动，滚动体只有自转和公转两个方向自由度，且未考虑润滑剂拖动性能的影响。韩勤锴等[14-15]基于Euler方程建立了能够预测滚动体打滑行为的空间三维非线性动力力学模型，分析了轴向径向联合载荷作用下，球的滑动速度随时间和空间的变化规律，结果表明径向载荷的引入使得滚动体的打滑速度出现波动，提高径向载荷，将显著增加打滑速度波动的幅值和范围。王云龙等[16]建立了角接触球轴承-转子系统的动力学分析模型，研究了润滑剂黏度、保持架引导方式和轴向预紧力对轴承启动加速和停止减速过程中滚动体打滑的影响。但其模型中对球与保持架的相互作用进行了简化。张东光和牛蔺楷[17]基于Gupta模型建立了考虑保持架效应及沟道表面波纹度的动力学分析模型，分析了表面波纹度波数和幅值对保持架打滑率的影响。袁倩倩等[18]建立了考虑轴承保持架兜孔和滚动体润滑状态和碰撞过程的保持架动力学模型，分析了轴承工况及引导-兜孔间隙比对保持架打滑率的影响。但是该研究没有考虑保持架间隙对滚动体瞬时冲击打滑的影响。

综上所述，目前对于联合载荷下滚动体进入和离开承载区时的打滑以及变速工况下球与滚道的拖动打滑已有不少研究，但是对于球与保持架的冲击碰撞导致的瞬时滑动研究还比较少。在联合载荷工况下，球在不同角位置处的接触角不同，球的公转速度呈周期性变化，而保持架的速度是所有球公转速度的平均值，受保持架兜孔间隙的限制，球与保持架会发生频繁碰撞，从而引起球与滚道的冲击滑动。因此，本文作者将以动力学模型为基础，以某高速角接触球轴承为研究对象，探究轴向径向联合载荷作用下，保持架兜孔间隙对滚动体冲击滑动的影响，从而为优化保持架结构设计和提高轴承动态性能提供理论依据。

1 角接触球轴承动力学模型

根据GUPTA[9]滚动轴承动力学建模方法，建立了高速角接触球轴承动力学模型。模型中假定轴承组件的质心与其几何中心重合；球和保持架具有6个自由度，外圈质心固定，内圈质心具有3个自由度，且内外圈均可绕其轴线转动。由轴承组件的质心运动方程和动量矩方程，并与运动学方程联立，通过变步长四阶Runge-Kutta方法求解，即可描述轴承组件的一般运动规律。球与保持架的相互作用模型及球与滚道的润滑拖动模型简要介绍如下，详细建模过程及模型验证参见文献[19-20]。

1.1 球与保持架的相互作用模型

球与保持架的相互作用示意图如图1所示。球与保持架兜孔之间不考虑流体动压作用，由Hertz接触理论计算法向力，Coulomb摩擦定律计算切向力。

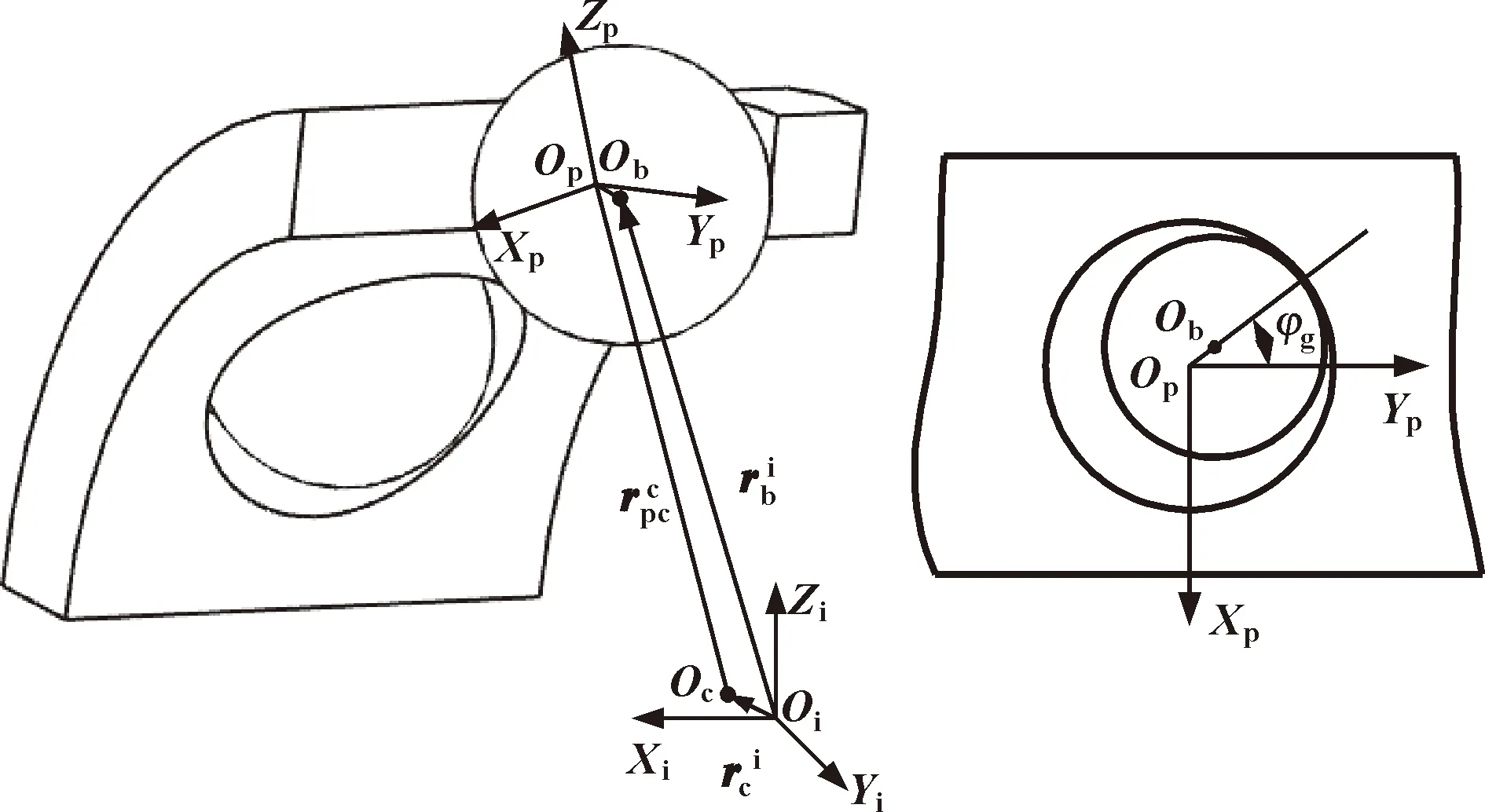
图1 球与保持架兜孔的相互作用示意Fig.1 Schematic of the interaction between the ball and the cage pocket

(1)

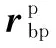
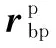
(2)

式中：Tpg=T(0,0,φg)为从兜孔坐标系到接触坐标系的转换矩阵。

球与兜孔的接触变形量为

(3)

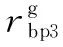
球与兜孔之间的法向力计算公式为

(4)

式中:Kbc为球与保持架兜孔的载荷-变形系数。

则球与兜孔之间的切向力为

Ftc=μcQc

(5)

式中:μc为球与兜孔之间的摩擦因数，设为恒定值0.05。

接触点处保持架相对球的滑动速度矢量为

(6)

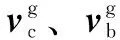
保持架和球的速度计算较为复杂，详细参考文献[19]。

则滑动速度的大小为

(7)

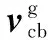
对于保持架与球及引导套圈的相互作用，由于滑动速度较大且接触区较小，可以作为点或线接触来计算瞬时磨损率，且一般认为磨损主要发生在保持架上。根据Archard磨损公式[21]，保持架单个兜孔的瞬时磨损率计算公式为

(8)

式中:Kc为保持架的磨损系数;Hc为保持架材料的布氏硬度。

得到了任意时刻的瞬时磨损率，即可计算时间T内的平均磨损率：

(9)

1.2 球与滚道的润滑拖动模型

对于球与滚道的接触，在接触椭圆内压力和滑动速度的变化较大。然而，由于接触椭圆的短半轴一般较窄，滑动速度沿短轴的变化可以忽略，可将接触区域沿长轴等距条形划分，如图2所示。接触坐标系的原点固定在接触椭圆中心，Xt轴沿椭圆长轴方向，Zt轴沿接触面法向。

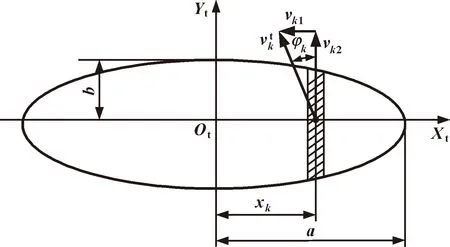
图2 接触椭圆内窄条中心处的滑动速度Fig.2 Sliding velocity at the strip center of the contact ellipse

窄条中心处外圈相对球的滑动速度矢量为

(10)

每个窄条中心处的滑动速度和等效载荷可表示为

(11)

(12)

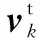
窄条中心处的切向力计算公式为

Ftk=μkQk

(13)

式中：μk为拖动系数，与窄条中心处的油膜厚度和滑动速度有关。

球与滚道之间的润滑状态可能是完全弹流润滑，也可能是混合润滑，甚至是边界润滑。混合润滑状态下球与滚道的接触力一部分由微凸体承担，另一部分由弹流油膜承担，微凸体承担的载荷比可根据油膜参数计算，油膜参数定义[2]为

(14)

式中：σb、σr分别为球和滚道表面粗糙度的均方根值，取为1.25Ra；hc为接触中心油膜厚度。文中分析取滚道表面粗糙度Ra=0.032 μm，球表面粗糙度Ra=0.02 μm。

球与滚道的等效拖动系数[22-23]可表示为

μe=μbqb+μh(1-qb)

(15)

式中：μb为边界润滑拖动系数，一般取为0.1[2]；μh为弹流润滑拖动系数。

润滑剂拖动曲线是滑动速度的函数，可通过试验获得。目前暂无所用的润滑剂拖动性能试验数据，文中采用两斜率模型代替[24]。

(16)

qb为粗糙表面微凸体承担的载荷比，由如下经验公式[22]计算：

(17)

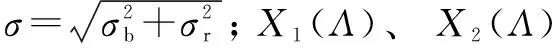
(18)

2 结果与分析

利用已校验的球轴承动力学模型[19-20]，以某高速角接触球轴承为算例，分析了联合载荷工况下时变转速和不同保持架兜孔间隙对球与滚道的冲击滑动和零件磨损率的影响。根据Archard磨损公式，时间平均磨损率与磨损系数成正比，目前分析中引用文献[21]中的磨损系数计算得到磨损率的变化趋势。轴承结构和材料参数列于表1和表2中。轴向预紧力为200 N，径向载荷为300 N。

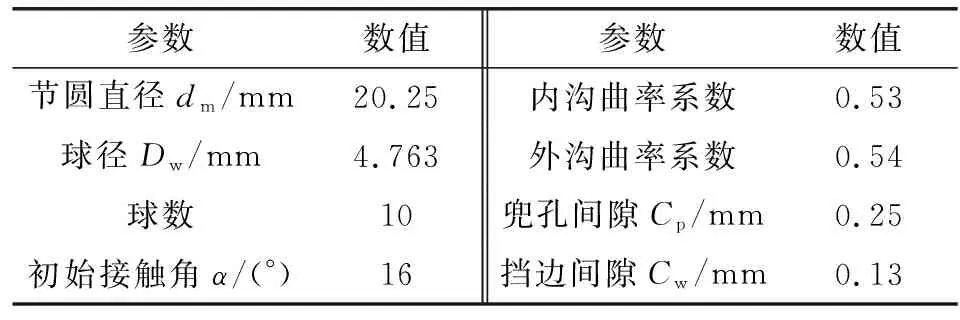
表1 轴承主要几何参数Table 1 Bearing geometry parameters

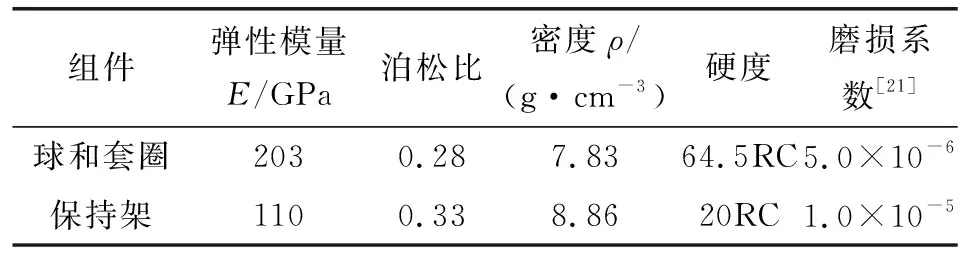
表2 轴承材料性能参数Table 2 Bearing material properties

2.1 变速工况下的结果

某涡轮起动机用高速角接触球轴承，内圈转速在0～120 000 r/min之间变化，加速过程不大于40 s，减速过程不大于60 s。因动力学分析计算量大，不能按1∶1的时间进行仿真，根据加减速时间计算得加速过程加速度为每秒3 000 r/min，减速过程加速度为每秒-2 000 r/min。加速阶段从114 000 r/min开始，加速2 s至120 000 r/min，恒速运行1 s，然后再减速3 s，至114 000 r/min，总仿真时间为6 s。内圈转速随时间的变化如图3所示。动力学仿真输出结果如图4、5所示。

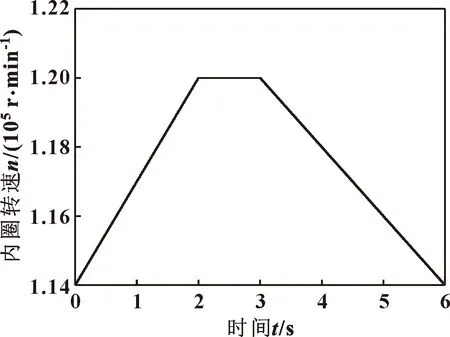
图3 内圈转速随时间的变化Fig.3 Change of the inner ring speed with time

图4所示为1#球公转角速度与保持架角速度随时间的变化。由图4(a)可以看出，由于轴承承受轴向径向联合载荷，转动过程中球的公转角速度呈周期性变化，且球公转角速度变化幅度大于保持架角速度变化幅度。这是因为保持架随球组转动，其角速度是所有球公转角速度的平均值，变化幅度相对较小。同时，从加速到稳定及稳定到减速的转变过程中，球和保持架的角速度没有明显突变。由此说明，在加速-恒速-减速过程中，球和保持架没有出现明显的整体打滑现象。而且，由于动力学仿真的时间步长为2.0×10-7s，时间增量极小，对于任意加减速过程都可认为是平稳连续的变化。因此，在给定工况下轴承不发生整体打滑，加减速过程及恒定转速下球与保持架的运动特性变化不大。图4(b)所示为恒速阶段2～2.01 s内球与保持架的角速度变化。可以看出，球的公转角速度周期性变化，每个周期的上升和下降阶段都存在瞬时突变。

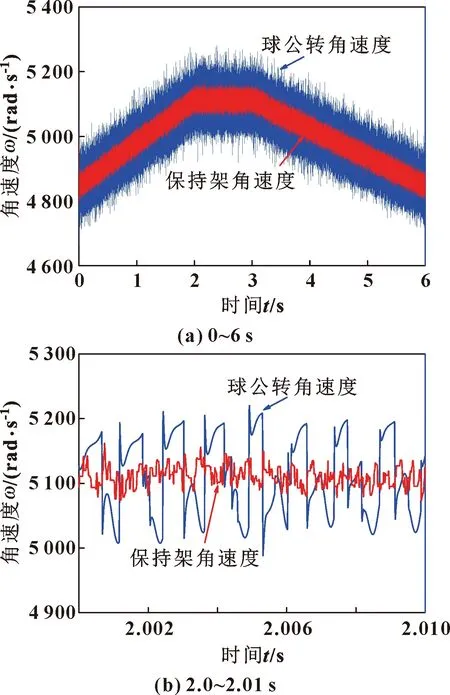
图4 1#球公转角速度与保持架角速度随时间的变化Fig.4 1# ball revolution and cage rotation angular velocity changes with time：(a)from 0 to 6 s;(b)from 2.0 s to 2.01 s

图5所示为在恒速阶段2～2.01 s内，1#球与内外圈的接触角、旋滚比、法向力及切向力的变化。可以看出，由于球的公转运动的周期性，这些参数均呈周期性变化。图5(a)中球与内圈的接触角整体上大于外圈，这是因为在球的离心力及外载荷作用下，球与内圈接触角相对初始接触角增大，而球与外圈的接触角减小。图5(b)中球与内外圈的旋滚比表明，球在内外滚道上均发生自旋，且球相对内圈的旋滚比大于外圈，表明球主要在内圈上发生自旋。图5(c)中球与外圈的法向接触载荷大于内圈，这是因为外圈接触角较小且球的离心力作用于外圈。

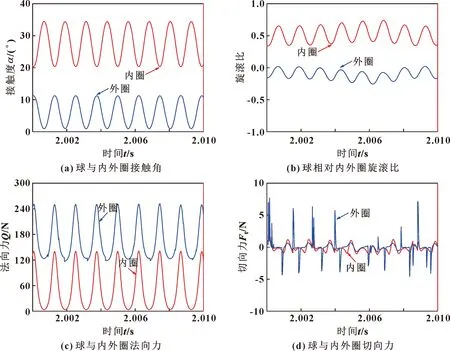
图5 恒速阶段2.0～2.01 s内1#球与内外圈的接触参数变化Fig.5 Change of contact parameters between 1# ball and inner and outer rings from 2.0 to 2.01 s at constant speed:(a)contact angle between ball and inner and outer rings;(b)roll ratio of ball to inner and outer rings;(c)normal force between ball and inner and outer rings;(d)tangential force between ball and inner and outer rings

图5(d)所示为球与内外圈的切向力，球与外圈的切向力有尖峰，且有一定周期性，球与内圈切向力的大小和方向呈现周期性变化，同时也存在与外圈切应力尖峰对应的小峰值，说明球与内外圈存在同步的冲击滑动。结合图4(b)中对应时刻球的公转角速度发生突变，可以推断，球相对内外圈的冲击滑动是由保持架与球的碰撞产生的，球与外圈的法向载荷较大，冲击滑动产生的切向力峰值较大，球与内圈的法向载荷较小，冲击滑动产生的切向力也较小；球在进入和离开径向载荷区时与内圈切向力的大小和方向都有规律性的变化，且与球公转速度的变化相关联，说明球与内圈存在滑动，即球相对内圈发生了打滑，但这个过程是渐进的，相对平稳。由此说明，球在内圈滚道上同时存在打滑和冲击滑动。

根据图5(c)、(d)及图4(b)的对应关系还可以看出，当球进入径向载荷区域时，球的滚动阻力增大，公转速度开始降低，但此时球公转角速度大于保持架角速度，球与保持架碰撞，推动保持架转动；当球逐渐离开径向载荷区域时，滚动阻力减小，公转速度开始增加，此时保持架的角速度大于球的公转角速度，保持架与球碰撞，推动球加速运动，直至下一次与保持架相碰，如此完成一个周期运动。

2.2 不同保持架兜孔间隙的结果

为进一步分析保持架结构参数对球与滚道冲击滑动的影响，在给定工况下只改变保持架兜孔间隙，分别取兜孔间隙Cp=0.2,0.25,0.32 mm，得到分析结果如图6、图7所示。

图6所示为恒定转速阶段不同保持架兜孔间隙对应的保持架角速度。由图6(a)可以看出，兜孔间隙增大，保持架角速度整体上增大。为便于比较，图6(b)示出了恒速阶段2.0～2.01 s内保持架角速度的均值随兜孔间隙的变化，可以直观地看出，保持架角速度随兜孔间隙增大而增加。由此说明，兜孔间隙增大，减少了球与保持架兜孔的碰撞，球与滚道的冲击滑动随之减小，从而球的公转角速度和保持架角速度增加。

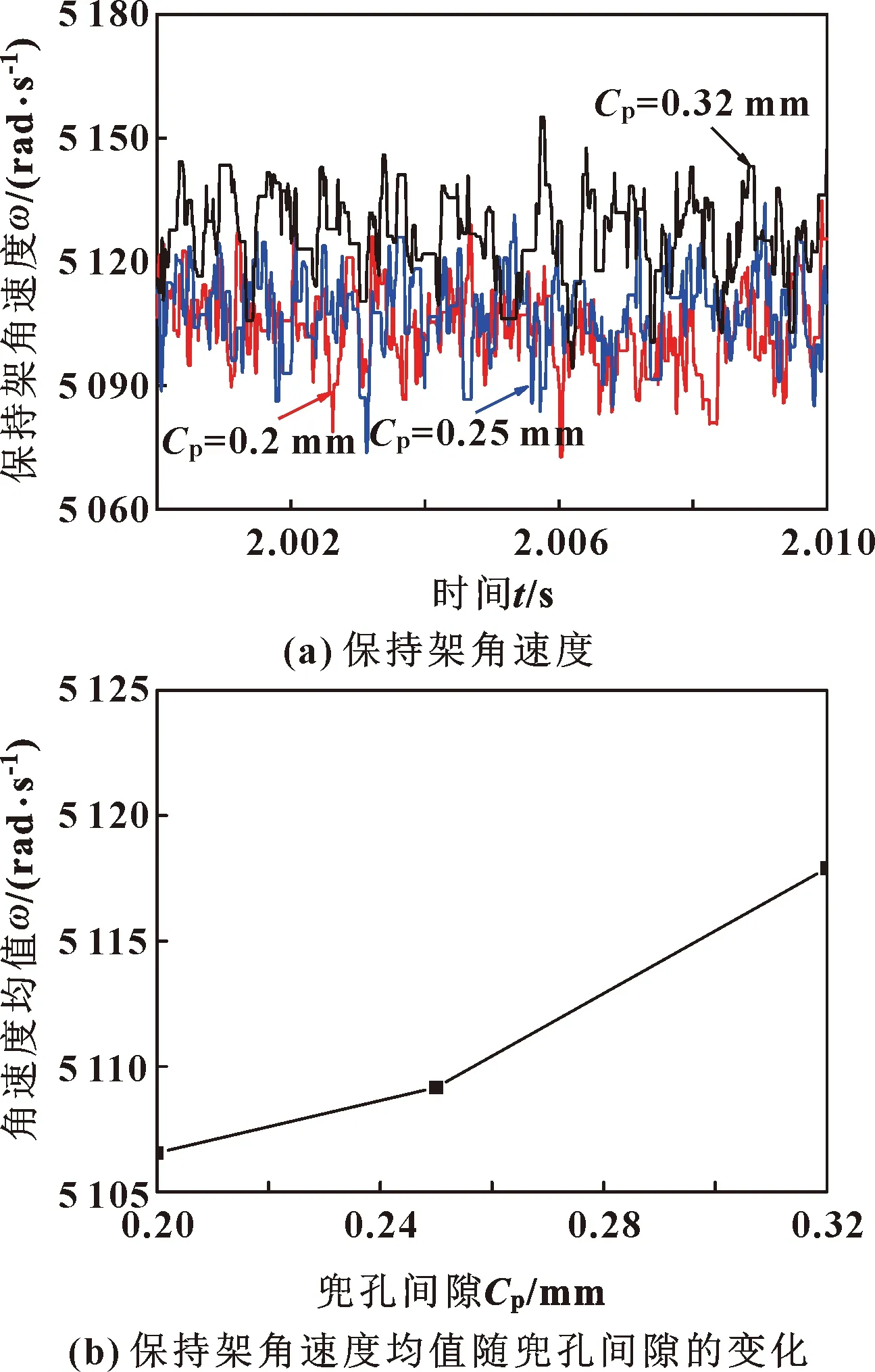
图6 恒速阶段2.0～2.01 s保持架角速度与兜孔间隙的关系Fig.6 The relationship between cage angular velocity and pocket clearance from 2.0 s to 2.01 s at constant speed： (a)cage angular velocity;(b)variation of average cage angular velocity with pocket clearance

图7所示为不同兜孔间隙下1#球与保持架兜孔沿滚动方向的碰撞力。可以看出，整体上兜孔间隙增大，球与保持架兜孔的碰撞力减小。表3给出了恒速阶段(2.0～2.01 s内)1#球与保持架兜孔碰撞力大小的分段统计，比如碰撞力θc≥25 N，对应不同保持架兜孔间隙的碰撞次数分别为1 017、995、776，说明球与兜孔碰撞的频率也随着兜孔间隙增大而减少。

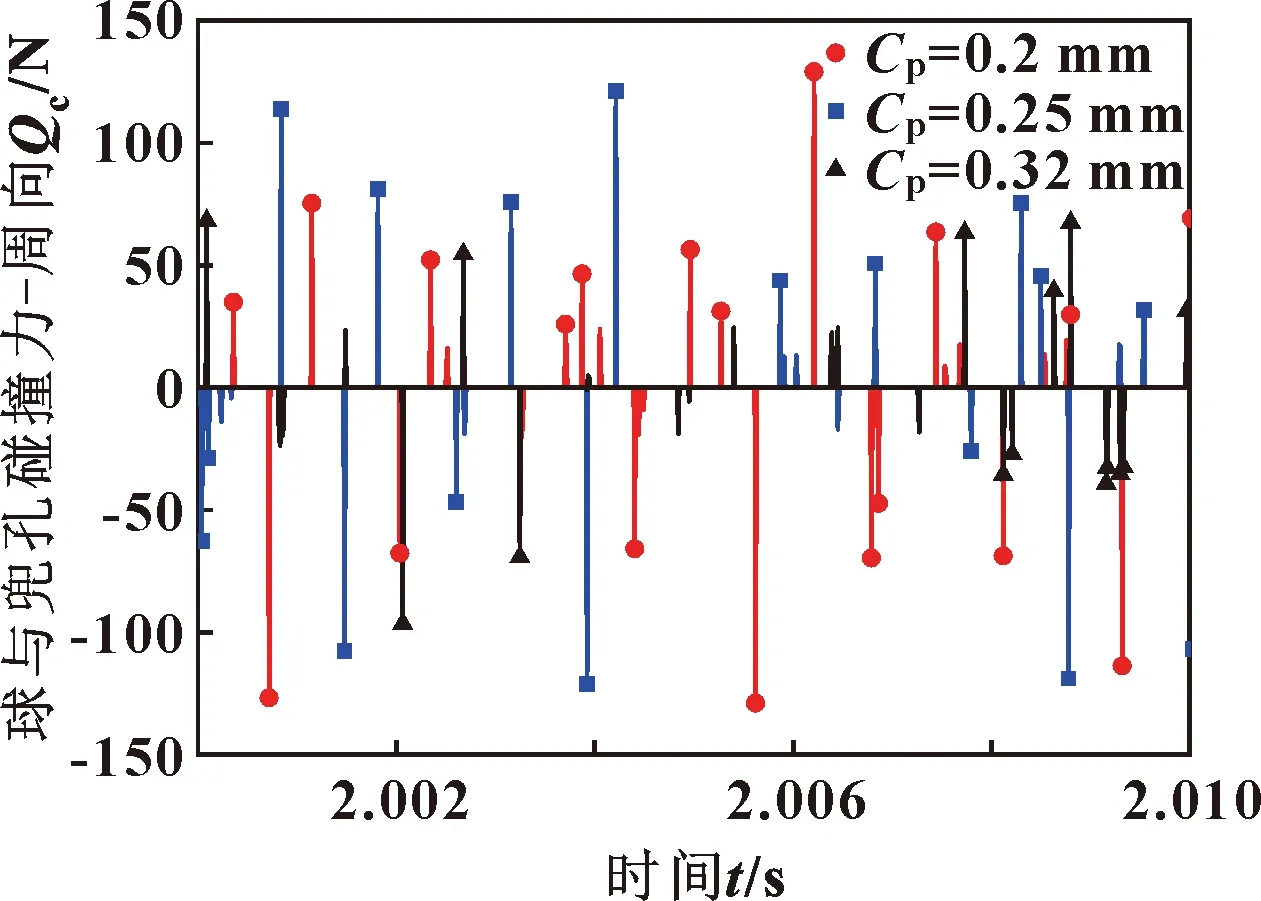
图7 不同保持架兜孔间隙下1#球与保持架兜孔碰撞力Fig.7 Collision force between 1# ball and cage pocket under different cage pocket gaps

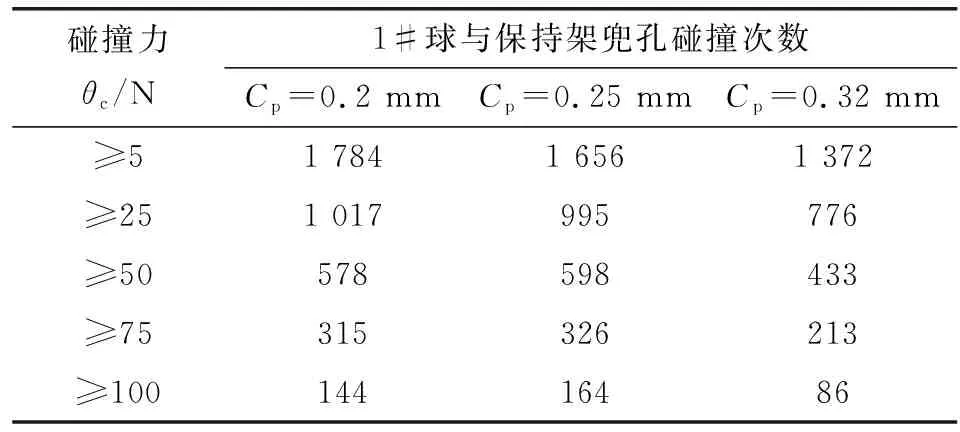
表3 恒速阶段2.0～2.01 s内1#球与保持架兜孔碰撞力大小分段统计Table 3 Sectional statistics of collision force between 1# ball and cage pocket from 2.0 s to 2.01 s at constant speed

保持架的时间平均磨损率综合反映了保持架与球相互作用力的大小和频率。图8所示为保持架兜孔(所有兜孔)不同磨损时间的平均磨损率。可以看出，随着兜孔间隙增大，球与保持架的相互作用减小，保持架兜孔的磨损率降低。

图8 恒速阶段2.0～2.01 s内保持架 兜孔不同时间的平均磨损率Fig.8 The average wear rate of the cage pockets at different time from 2.0 s to 2.01 s at constant speed

综合以上分析可以得出：承受轴向径向联合载荷的高速角接触球轴承，转动过程中球的公转角速度呈周期性变化，且球公转角速度变化幅度大于保持架角速度变化幅度。在给定工况下，从加速到稳定及稳定到减速的转变过程中球和保持架的角速度没有明显突变。球与内外圈的接触角、旋滚比、法向力、切向力随球的角位置周期性变化。由于球进入和离开径向载荷区域时公转角速度的变化，导致球相对内圈滚道打滑，同时球与保持架碰撞导致球相对内外圈的冲击滑动。为减小球与内圈的打滑可适当增大轴向载荷，降低球公转速度的变化幅值，从而减小球相对内圈的打滑。同时，为适应球公转速度的变化，保持架兜孔间隙应适当增大，以便给球的速度变化留足空间，从而减小球与保持架的碰撞及球与滚道的冲击滑动。

3 模型验证

球与保持架的碰撞及球与滚道的冲击滑动等动态现象具有瞬时性，试验不容易测量。通过与文献[9]中的2号角接触球轴承算例进行对比，以验证理论仿真的结果。轴承的结构、润滑参数与文献[9]中表8-2的相同，工况为内圈转速30 000 r/min，推力负荷5 000 N，旋转径向负荷4 000 N。文中计算结果与文献[9]滚动轴承动力学分析软件ADORE的结果对比示于图9，图中所示为1#滚动体的结果。可以看出，滚动体的轨道速度呈周期性变化，同时存在一些尖峰，说明存在冲击滑动。文中计算的滚动体轨道速度与文献[9]计算的结果变化趋势一致，数值上也较为接近，误差约为1.86%，出现尖峰的位置也大致相同。以上验证了文中仿真结果的正确性和可靠性。

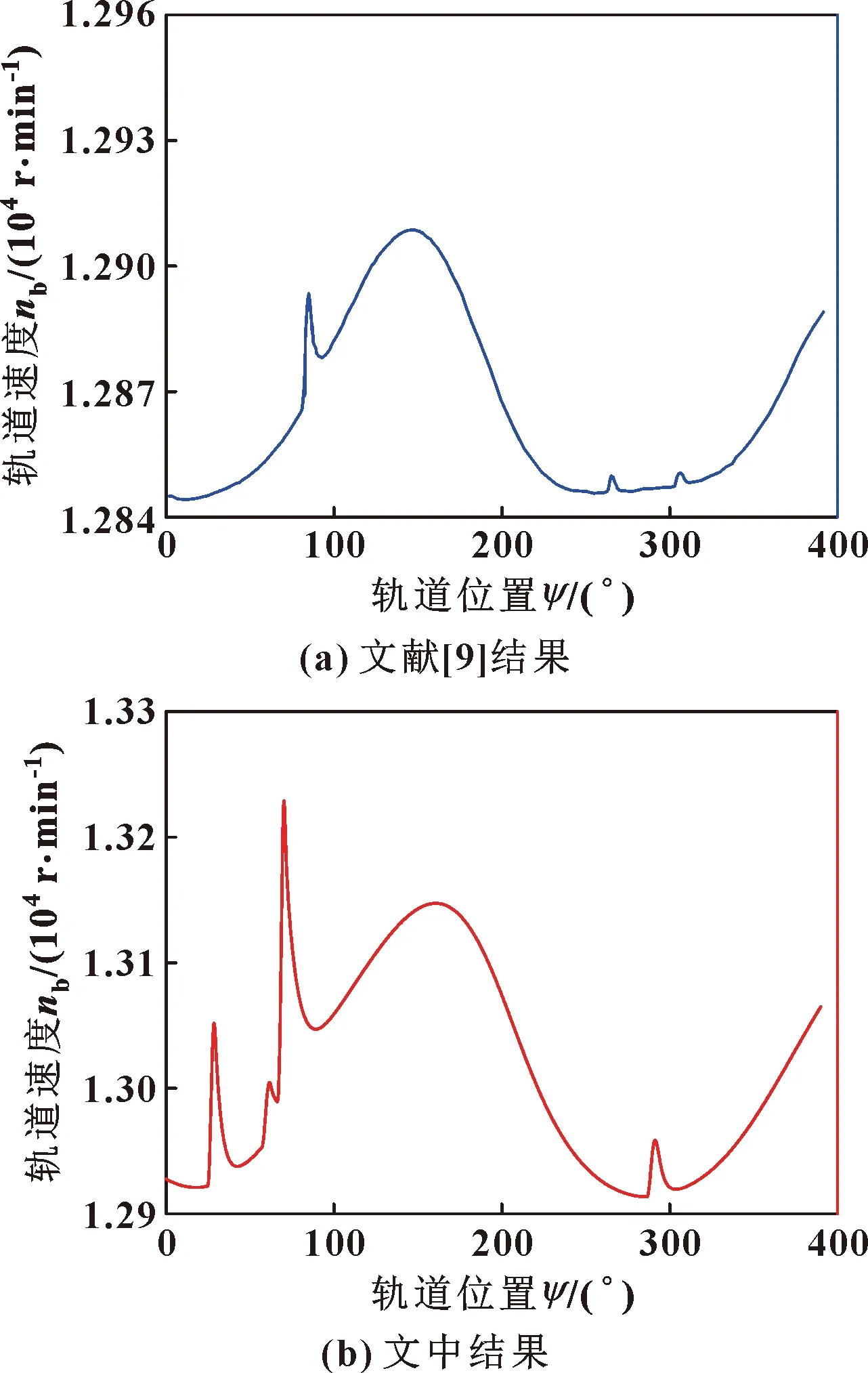
图9 文献[9]中角接触球轴承算例中1#滚动 体的轨道速度和文中计算结果的比较Fig.9 Comparison between the orbital speed of the 1# rolling element of the angular contact ball bearing example in reference 9 and the calculation results in this paper

4 结论

(1)联合载荷下高速角接触球轴承在加速-恒速-减速过程中球和保持架的运动呈周期性变化，且球的公转角速度变化幅度大于保持架的角速度变化幅度。

(2)对于承受联合载荷的高速角接触球轴承，由于球进入和离开径向载荷区域时公转角速度的变化，导致球相对内圈滚道发生打滑，同时球与保持架碰撞导致球相对内、外圈滚道发生冲击滑动。

(3)适当增大保持架兜孔间隙可以减小滚动体与兜孔的碰撞，从而降低球与滚道的冲击滑动，同时也有利于降低保持架的磨损率，提高轴承的动态性能和使用寿命。