联合收割机与运粮车协同作业调度技术研究*
李文鑫,张璠, 2,姚竟发, 2,常淑惠, 2,郭亚倩
(1. 河北农业大学信息科学与技术学院,河北保定,071000; 2. 河北省农业大数据重点实验室,河北保定,071000)
0 引言
在现代农业中,农村土地经营方式逐渐由分散经营转向集中经营。既要关注粮食安全,也要考虑土地的经营效率[1]。随之对农业机械配置与路径的规划要求也愈来愈高,多台联合收割机间的协同作业虽然有效提高机械利用率与作业效率,但没有运粮车的及时响应将导致整体作业时间增长,浪费农机资源。因此对于多台联合收割机完成多约束复杂农田任务,需要配备精确合理的运粮车响应,这不仅节约了农机机械成本,并且对整个田间运输效率的提升具有重要意义。
国内外针对农业机械调度问题主要集中在田间农机资源调度与路径规划的问题上,根据不同的农机调度类型可整体分为有无运粮车响应的收割机间协同调度的农田作业问题。面对多农机调度问题,Conesa-Muoz等[2-3]使用模拟退火方法的元启发式算法提出较为通用的农机调度路径规划算法,解决了车辆同质和车辆异质的农机路径规划问题。Seyyedhasani等[4-5]考虑了多辆农机协同作业的情况,将农机调度问题转换为车辆调度问题,使用改进Clarke-Wright算法和禁忌搜索算法提供合理的农机作业路径规划和调度方案。林涛等[6]在分析车辆路径问题的基础上,将其转换为经典TSP优化问题进行求解,提出了一种改进的遗传算法,在加快寻优速度的同时防止陷入局部最优。曹如月[7]、张小花[8]类比旅行商问题,采用蚁群算法求解多机协同作业任务规划问题,但未将农机在田间作业的约束进行综合考虑。刘正伟等[9]以秸秆回收机械的综合成本问题为研究目标,综合考虑秸秆回收机械路径和作业冲突的情况,避免回收农机路径重复冲突的问题。Utamima等[10-11]提出进化混合邻域搜索算法和进化分布式评估算法来优化非作业路程。Cariou等[12]提出了基于回旋曲线的掉头方法,Boryga等[13]提出了基于多项式曲线的掉头路径规划方法。姚竟发等[14]以总作业时间和作业时长为综合优化目标,考虑联合收割机和作业冲突的情况,提出联合收割机多机无冲突协同作业路径优化算法,但尚未考虑加入运粮车的响应。王雪阳等[15]基于启发式优先规则农机调配策略,在农机充足的条件下,多机并行任务采用收益最大的农田作业点优先调配规则进行分配,实现整个工程最小化的调度成本。艾长胜等[16]为提高植保机器人在路径规划中的准确度与可靠性,对果园信息进行预处理实现精确作业,但没有对农田进行全局路径规划。而对于多台联合收割机与运粮车的响应调度问题,李世超[17]研究了一种跟随式农机主从导航系统,从机根据位姿信息生成预设路径,并跟踪主机作业,初步实现了主从导航协同作业。曹光乔等[18]将农田区域定义为任务单元,探究收割机与运粮车的响应模式,最大化地减少了收割机非生产性的作业时间。He等[19-20]将收割机收割与运粮车运输问题视为一个带动态卫星的多行程车辆路径问题,依据运粮车需要响应的具体位置的动态变化,提出了一种启发式算法的最优解,且属于概念性的调度响应问题。Jing等[21]围绕实现农业资源分配和配送车辆协同调度的高效智能优化,提出一种改进的强化免疫算法,提高了算法的自适应性和全局搜索能力。
综上所述,现有研究尚未能解决基于联合收割机与运粮车的多机协同调度问题,因此本文综合考虑了联合收割机粮仓容积、运粮车协同作业等因素,以最小化联合收割机总生产性作业时间和总非生产性作业时间为目标,构建了基于多机多目标的协同优化调度模型,设计了基于改进蚁群算法的优化算法,为解决联合收割机与运粮车间的协同调度问题提供了解决思路。
1 多机协同作业优化调度问题分析
1.1 问题描述
本文主要研究多台联合收割机作业路径优化以及基于联合收割机与运粮车的协同调度问题。多联合收割机在田间作业路径规划和运粮车的调度示意图如图1所示。

图1 多机路径规划与调度示意图
由图1可知,多台联合收割机在一块农田地块上作业过程中,若粮仓装满后,需要运粮车的辅助完成卸粮,然后才能继续开展收割作业。因此本文将在多联合收割机作业优化路径的基础上,研究联合收割机与运粮车的协同优化调度方案。
本文简要描述如下:以总非生产性作业时间最短为目标,计算m台联合收割机在一块农田上的最优化作业路径,接着综合考虑u台运粮车辅助m台联合收割机协同卸粮的情况,以联合收割机非生产性作业等待时间最短为目标,计算联合收割机与运粮车的动态协同调度策略。按照作业行序列集进行收割与卸粮任务,假定联合收割机的粮仓容积为Cz,在t0时刻收割机粮仓达到容积V′时,依据相对距离最近原则向运粮车发送信号使其进行与收割机之间的协同调度,并依据在t0时刻后收割机与运粮车行驶路程的大小进行判断收割机是否产生等待时间,再依据实际情况卸粮。保证运粮车及时完成卸粮任务。
针对本文的研究内容,特做以下说明。
1) 每个作业行只允许一台收割机遍历1次。
2) 联合收割机连续作业至满仓,完全卸粮后再进行下次作业。
3) 根据安装在联合收割机与运粮车上的传感器可以实时获取其位置信息。
4) 农机作业过程中不考虑农机故障与田间遇到障碍物的情况。
5) 联合收割机的型号相同,且作业能力相同;运粮车的型号、作业速度等均相同。
6) 假设农田地块的形状是规范的矩形,根据联合收割机作业幅宽,将农田划分为等宽的若干作业行。
7) 联合收割机与运粮车都从同一个位置出发,联合收割机完成作业、运粮车卸粮后也回到该出发点,等待。
1.2 模型构建
为方便问题描述与模型构建,对相关变量做以下描述。
1) 农田作业行集合N={n1,n2,n3,…,ni},即按照作业总行数从左向右进行农田顺序编号。以locNi和SNi分别表示农田入口位置坐标与农田面积,i∈N*。
2) 农机机群分别表示为:联合收割机群ME={m1,m2,m3,…,mz},以mz表示第z台收割机,其属性描述为mz={Cz,tz,Vz,Vz′}。其中,Cz表示收割机粮仓容积,tz表示联合收割机的等待时间,Vz表示联合收割机直线作业速度,Vz′表示收割机转弯作业速度,收割机粮仓喂入量为h。运粮车集群表示为YU={u1,u2,u3,…,uy},以uy表示第y台运粮车,其属性描述为uy={Cy′,Vy′},Cy′表示运粮车的粮仓容积,且满足Cy′≥Cz,Vy′表示运粮车的作业速度。
3) 联合收割机在农田地头主要有Ω型和U型两种转弯方式。Ω型转弯不仅作业时间长且操作难度较大,对比U型转弯作业时间短、操作简便的特点,如果要得到更好的联合收割机路径优化效果,需尽量采用U型转弯。具体公式表述为
U(d)=d·w+(π-2)rmin
式中:U(d)——转弯距离;
w——农机作业幅宽;
rmin——农机从i行到j行的最小转弯半径;
d——转弯时两作业行间的度量,d=|j-i|,i≠j;
i——农机作业结束行的序号;
j——农机作业进入下一行的行号。
4) 作业任务序列集Rz={{0,i1,i2,i3,0},{0,i4,i5,i6,0}…},以Rz表示第z台联合收割机的作业路径序列集。
具体目标函数与约束条件分别表示如下。
联合收割机以总生产性作业时间最短的优化目标
minT1=(Disz+Disz′)/Vz
(1)
联合收割机以最小化总非生产性作业时间为优化目标
minT2=T′
(2)
(3)
约束条件
iz0=i|Rz|+1=0,{i1,…,i|Rm|}⊆N�}
(4)
(5)

(6)
式中:T1——联合收割机总作业时间;
T2——运粮车作业等待时间;
T′——根据运粮车和联合收割机的相对位置关系,判断是否产生等待时间;
iz0——联合收割机出发点;
iu0——运粮车出发点;
Nz——每行只被一台联合收割机作业;
Disz——联合收割机进行直线作业的总距离;
Disz′——收割机转弯作业时总路程;
父子关系、成员关系所具有的传递性,对于概念网络的扩展起着决定性的作用。在类比推理过程中也可以作为规则使用。
Ly——运粮车在t0时刻后前往运粮所行驶的路程;
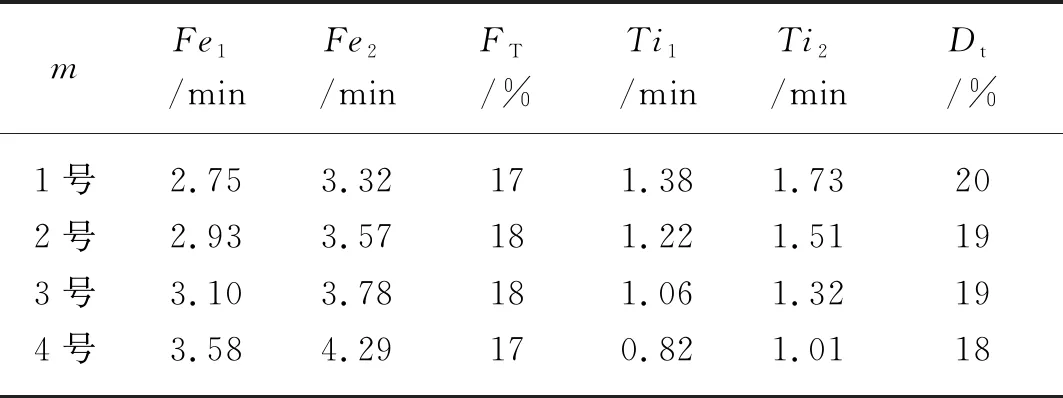
Lz——联合收割机在t0时刻后行驶的路程,当Ly i|Rz|——第z台联合收割机从收割起始点到结束的作业总路径集; i|Ru|——第u台运粮车从出发点到运粮结束的作业路径。 其中式(4)表示联合收割机从出发点出发,作业结束后返回出发点。式(5)表示运粮车从出发点出发,作业结束后返回出发点,式(6)表示每行只能被一台联合收割机访问一次。 根据构建的调度模型,本文研究的基于联合收割机与运粮车的协同优化调度问题可分为两阶段来研究与求解。问题求解流程如图2所示。 图2 问题求解流程图 首先采用MMCOSA算法以联合收割机总非生产性作业时间最短为目标,求解多联合收割机的初始路径规划方案。其次以减少联合收割机非生产性作业等待时间为目标实现联合收割机与运粮车的动态协同调度。 1) 首先对算法参数初始化。包括种群规模M、作业行数N、迭代次数t、信息启发因子α、期望启发式因子β。 2) 给定农田行初始序列如N={1,2,…,15},随机打乱顺序,依据状态转移规则式(7)从当前农田行选择下一个要访问的农田行,最终分组形成初始完整路径集。之后引入2-opt法,对产生的最优路径序列随机交换其中任意两条路径,对此时新生成的路径长度进行判断,若路径长度优于未改变路径,则保留进行迭代,否则舍弃,需再次重复上述过程。如Rz中其中一条序列N1={0,3,5,9,0}经2-opt法交换后变成N2={0,5,3,9,0},若N2表示的路径长度小于N1,则农机采用N2序列。否则重新选择两条新路径进行交换。 (7) α——信息启发因子,表示行驶路径的相对重要性,α值越大蚂蚁选择以前经过的路线的可能性越大,但过大会使搜索过早陷于局部最小解; β——期望启发因子,它的大小表明蚂蚁选择离它近的农田行的可能性也越大; Rk——尚未访问过的农田行序列; ηij(t)——启发函数,ηij(t)=1/Nij,表示蚂蚁从农田行i转移到行j时距离的倒数,当两农田行的距离越短时,信息素浓度越大的路径越容易被选择; τij——从行i到j时留下的信息素大小; τij(t+1)——农田i到j上的信息素含量,每被访问1次或1个访问循环结束后,路径上残留的信息素会被重新处理,进行信息素的更新。 其中,路径上残留信息素的处理规则如下 (8) 式中: (1-ρ)——信息素残留系数,规定ρ∈(0,1); (9) 式中:Q——信息素强度; Lq——第q只蚂蚁在本次循环中所走的路径总长度,如当得到其中一条路径为{0,1,3,5,0}时,联合收割机作业各路径长度Lu=527 m。 综上最终求得农田作业序列集Rz以及联合收割机作业各路径长度Lu。 1) 在t0时刻联合收割机向运粮车发出信号,运粮车在t0时刻后出发前往卸粮点。 2) 若运粮车行驶路程大于联合收割机在t0时刻后行驶距离时,联合收割机不产生等待时间且用0表示;否则联合收割机将产生等待时间tz。 3) 不考虑运粮车载量对车速的影响,通过改变运粮车的行驶速度及时满足联合收割机的卸粮信号,实现最大化地减少联合收割机的等待时间的调度目标。 当联合收割机作业幅宽w=4.2 m,最小转弯半径rmin=3.8 m时,本文对试验数据做出如下假设:(1)矩形农田大小为63 m×130 m(宽×长),面积为8 190 m2。(2)农田划分为等宽15行并进行编号。其中,i=0为调度中心,i∈{1,2,3,…,15}为农田行编号。(3)联合收割机直线行走速度为Vz=19 km/h,农田地头选择U型转弯方式,速度为Vz′,收割机粮仓容量Cz=2 t;运粮车载重2 t,速度为Vy′=26 km/h,tj为运粮车参与联合收割机卸粮的时间。假定收割机在开始收割 1 min 后向运粮车发出信号。(4)收割机粮仓喂入量为8 kg/s。(5)农机作业过程中不考虑故障、避障等外界因素的影响。假设当m=4,u=3时,收割机的台数分别用1~4号表示,运粮车用u1,u2,u3表示。本文运用pycharm软件对改进后的算法进行测试。初始参数设置为α=1,β=5,Q=10,ρ=0.3,蚂蚁数量M=100,最大迭代次数emax=300。 在多机协同优化调度算法中采用2-opt法产生4条联合收割行驶路径以及作业序列,如表1所示。 表1 联合收割机静态规划方案Tab. 1 Static planning scheme of combine harvester 由表1可知,联合收割机载重2 t时,1号联合收割机的路径序列为{0,3,6,11,0},行驶路程为516 m;2号联合收割机的路径序列为{0,5,2,9,13,8,0},行驶路程为902 m;3号联合收割机的路径序列为{0,1,4,7,10,0},行驶路程为709 m;4号联合收割机的路径序列为{0,14,12,15,0},行驶路程为516 m。 根据表1中4台联合收割机的路径序列,表2中加入运粮车协同联合收割机作业,试验数据如表2所示。 由表2可知,根据不同联合收割机的路径序列,运粮车加入农田行作业的时间不同,同时产生不同的等待时间。如运粮车u2、u3在1号联合收割机开始作业后的10.9 min、15.2 min分别进入{0,3,6,11,0}农田行辅助卸粮,当联合收割机粮仓满载时,此时运粮车刚好到达,即联合收割机产生的等待时间为0。 本研究为避免单一试验的偶然性,通过改变联合收割机直线行驶速度,当Vz分别为20、23、26、29 km/h时,分别测试4台联合收割机是否产生等待时间。测试不同速度各10组取平均值共40组试验数据如表3所示。 表2 联合收割机与运粮车协同作业调度方案Tab. 2 Cooperative operation scheduling scheme of combine harvester and grain truck 表3 联合收割机等待时间对比Tab. 3 Combine harvester wait time comparison 由表3可知,当联合收割机直线行驶速度Vz小于等于运粮车行驶速度Vy′时,联合收割机不产生等待时间。如1号联合收割机在Vz=20 km/h时,行驶路程共582 m,产生等待时间为0。因此满足本研究的调度目标,最大化缩短了农机协同作业调度的时间,同时减少了农机资源的浪费。 假设在农田划分为40行且运粮车行驶速度Vy′=26 km/h条件下,采用多机协同优化调度算法(MMCOSA)与传统蚁群算法(ACO)针对联合收割机路径长度、总非生产作业时间与非生产等待时间进行对比。假定联合收割机粮仓满载2 t,作业速度为20 km/h,在第1 min时向运粮车发出信号;蚁群算法的初始参数设置为α=1,β=5,Q=10,ρ=0.3,蚂蚁数量M=100,最大迭代次数300次。 MMCOSA下的路径长度Lu1为7.3 km,得到序列集{{0,6,1,10,2,9,3,8,4,7,5,0};{0,16,11,20,12,19,13,18,14,17,15,0};{0,26,21,30,22,29,23,28,24,27,25,0};{0,36,31,40,32,39,33,38,34,37,35,0}},总非生产性作业时间Fe1为2.3 min,非生产作业等待时间Ti1为1.9 min;ACO下路径长度Lu2为8.7 km,得到序列{{0,34,27,35,30,31,23,20,6,13,1,0};{0,11,10,14,15,16,19,37,22,17,21,0};{0,33,32,25,29,28,26,24,12,36,0};{0,40,38,18,39,7,8,5,9,3,2,4,0}},总非生产性作业时间Fe2为2.8 min,非生产作业等待时间Ti2为2.4 min。因此,路径缩短率LT为19.18%、总非生产性作业时间缩短率FT为17.10%、非生产性等待时间缩短率Dt为20.8%。其中LT、FT、Dt分别用式(10)~式(12)表示。 (10) (11) (12) 式中:Lu1——在MMCOSA算法下4台联合收割机分别行驶的路径长度; Lu2——在ACO算法下4台联合收割机分别行驶的路径长度; Fe1——在MMCOSA算法下联合收割机的总非生产性作业时间; Fe2——在ACO算法下联合收割机的总非生产性作业时间; Ti1——在MMCOSA算法下联合收割机的非生产性等待时间; Ti2——在ACO算法下联合收割机的非生产性等待时间。 为验证多机协同优化调度算法对求解多联合收割机的初始路径规划的有效性和稳定性,试验数据如表4所示。 表4 非生产作业时间与等待时间对比Tab. 4 Non-production operation time versus waiting time 由表4可知,MMCOSA算法相比ACO算法总非生产性作业时间和非生产性等待时间均有所缩短,且非生产性作业时间缩短率平均达到17.5%,非生产性等待时间缩短率平均达到19.02%。如1号联合收割机的Fe1较Fe2缩短0.57 min,FT达到17%,Ti1较Ti2缩短0.35 min,Dt达到20%。综上,本文能满足农机作业调度的任务需求。 1) 为解决联合收割机作业路径规划不合理、联合收割机与运粮车无法协同优化调度等问题,本文综合考虑实际农田作业情况,以最小化联合收割机总非生产性作业时间和非生产性作业等待时间为目标,构建了多机型多任务协同优化调度模型,设计了多机协同优化调度算法(MMCOSA)。首先通过算法计算得到联合收割机的静态路径规划方案,即每台联合收割机作业路径及行驶里程数。接着根据MMCOSA得到的农机静态行驶路径,采用运粮车与联合收割机相对距离最近的优先策略实现联合收割机与运粮车的动态协同调度,判断联合收割机在t0时刻达到限定容积V′时,计算运粮车加入作业的时间及联合收割机的等待时间,最终计算得到联合收割机与运粮车协同作业优化方案。 2) 通过MMCOSA与ACO试验结果对比,当农田被划分成40行时,通过MMCOSA算法得到的总非生产性作业时间缩短17.5%,联合收割机等待时间缩短19%。通过计算不同农田行下收割机与运粮车试验数据,当行驶速度相同时,联合收割机总非生产性作业时间和非生产性作业等待时间平均缩短17.5%和19.02%。 3) 本文以缩短联合收割机在田间总非生产性作业时间与等待时间为目标,设计了多机协同优化调度算法,为研究联合收割机与运粮车协同作业调度问题提供了一种解决思路,但尚未考虑农田中存在障碍物的情况,在后续的研究中将会进一步完善研究内容。2 多机协同优化调度算法研究

2.1 路径规划方案实现步骤

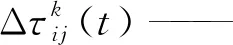

2.2 基于距离最近的优先级策略规则
3 算例分析
3.1 MMCOSA试验



3.2 不同算法对比分析
4 结论
——国外课堂互动等待时间研究的现状与启示

