基于DEM的玉米秸秆离散元模型参数标定*

童世合，邵明玺，曹猛，赵军杰

(1. 青海省特种设备检验检测院，西宁市，810005； 2. 青海大学，西宁市，810016)

0 引言

玉米秸秆是畜牧饲料的主要来源之一，也是一种重要的生物质能源[1]，玉米秸秆的深度加工对于饲料增收和生物质能源发展具有深远意义[2-3]。离散元法(DEM)用于研究离散物料在外部载荷下的运动学特性[4]，具有设计效率高、仿真精确度高和实际误差低等优点，尤其在农业领域得到广泛应用。

秸秆加工机械关键部件在设计时存在模具制作成本高、设计周期长、操作不灵活等问题，秸秆与机构之间的相互作用特性和规律难以通过常规技术手段进行观测，机构设计缺少可靠依据，导致已有的结构可靠性差、作业效果不理想，借助DEM法建立秸秆精细化仿真模型，开展机构的参数优化设计，有效提高秸秆生产效率。然而，秸秆离散元仿真模型在外形和材质等方面仍与实际具有一定差异，通过力学试验获得弹性模量、摩擦系数等关键参数通常不能够直接应用，需要对相关参数重新进行标定。

在农业物料仿真参数标定方面，国内外研究人员基于EDEM软件开展了大量研究，EDEM是一款基于离散元法的颗粒物料通用仿真软件。Adajar等[5]开展了油菜、玉米、小麦等5种作物的秸秆剪切特性标定，与实际值相对误差小于2%；Schramm等[6]利用EDEM开展了小麦秸秆弹性模量和泊松比标定，与物理试验结果的相对误差仅为3.11%；Fang等[7]利用Plackett-Burman试验对玉米碎秸秆的堆积角进行了仿真参数的标定，结果表明仿真试验和物理试验的平均相对误差仅为0.29%，说明利用EDEM进行参数标定获得的结果准确性好，具有较高的精度；张涛等[8]为了提高玉米秸秆揉碎过程的仿真精度，开展了秸秆—揉碎机、秸秆—秸秆接触参数的标定研究。

上述研究验证了离散元仿真方法的可靠性和准确性，但仿真过程中为了提高运算速度，不同程度地简化了秸秆模型，导致模型精细化程度不足。为此，本文针对秸秆外表皮质地坚硬、纤维排列规律且均匀、内瓤木质部质地偏软、组织紧密不规则的显著差异，建立了反映真实秸秆有茎节式样和无茎节式样的外表皮和内瓤性状的离散元仿真模型，结合单轴压缩试验确定仿真参数，并通过剪切试验进行验证，为后续秸秆加工机构的研制提供数据参考。

1 材料与方法

1.1 Hertz接触理论

Hertz接触理论是EDEM软件计算颗粒—颗粒和颗粒—几何体接触特性的理论基础，通过Hertz-Mindlin无滑移模型、Hertz-Mindlinwithbonding模型和Hertz-Mindlin JKR模型等基础模型建立真实情况下两物体之间的接触规则[9-11]。考虑到秸秆内部组织间的连接方式和表现出的各向异性特性，采用Hertz-Mindlinwithbonding将秸秆模型中的颗粒进行粘结，颗粒与颗粒之间接触作用如图1所示，法向、切向应力应变方程如式(1)所示。

(1)

式中：A——颗粒之间的接触面积，mm2，A=πRB2；

J——颗粒的转动惯量，kg·m2，J=πRB4/4；

RB——颗粒的接触半径，mm；

vn——颗粒法向运动速度，m/s；

vt——颗粒切向运动速度，m/s；

Fn——颗粒受到的法向作用力，N；

Ft——颗粒受到的切向作用力，N；

Mn——颗粒法向力矩，N·m；

Mt——颗粒切向力矩，N·m；

Sn——法向刚度系数；

St——切向刚度系数。

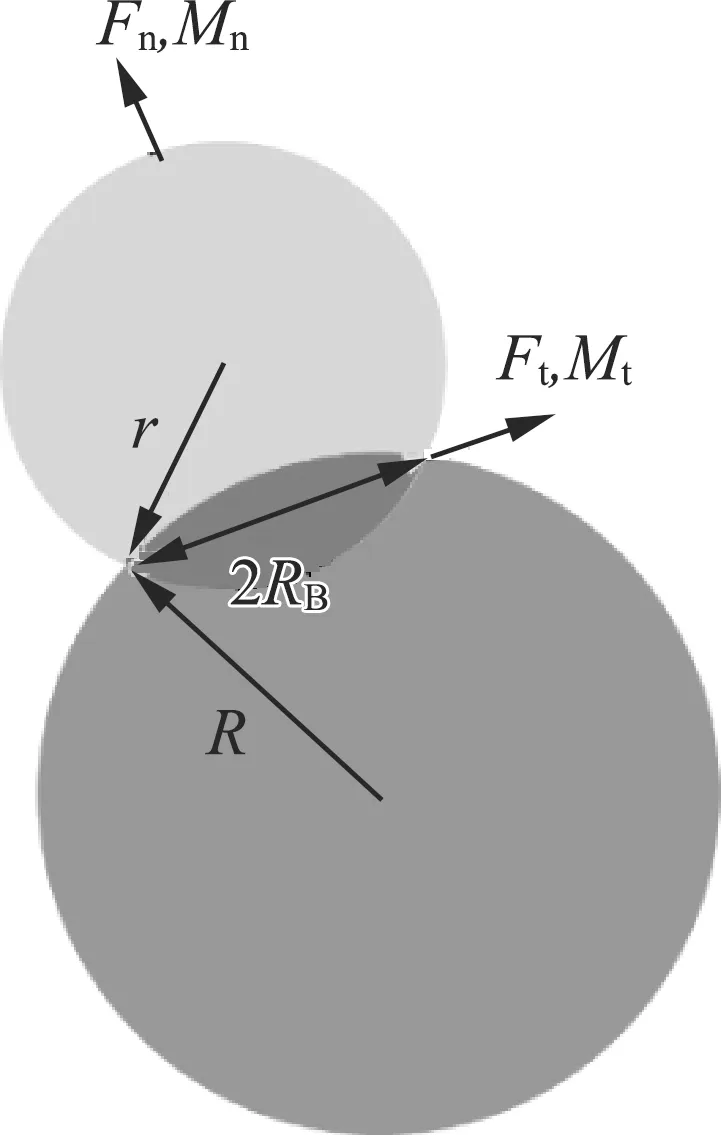
图1 球型颗粒接触示意图

式(1)反映了颗粒所受作用力与颗粒自身属性的关系，法向刚度系数、颗粒的弹性模量和半径相关，切向刚度系数、颗粒的剪切模量和半径相关，综上所述，颗粒粘结力的大小主要取决于法向刚度系数、切向刚度系数、临界法向应力和临界切向应力。

1.2 离散元仿真模型的建立

本文基于EDEM提出了一种快速构建精细化散粒物料颗粒的方法，具体构建方法如下。

1) 规定颗粒生成规则。考虑到秸秆外表皮和内瓤在形态和结构上存在较大差异，用于单轴压缩试验和剪切试验的秸秆直径为30 mm、长度为30 mm，外表皮模型采用直径为3 mm球型颗粒建立，内瓤模型采用0.5～1.0 mm球型颗粒建立。外表皮模型采用“分层叠加”的方法进行建立，秸秆直径根据测量结果设置为30 mm，因此每个底层颗粒的质心位置均匀分布在直径为30 mm的圆上，在空间直角坐标系中捕获颗粒的质心在X和Y轴上的坐标，Z轴坐标则以间隔4 mm 递增，制定颗粒坐标规则(部分)如图2(a)所示，将表中所有数据复制到Meta-particle面板中，建立外表皮模型如图2(b)所示。内瓤模型采用颗粒工厂模板内静态生成的方法进行建立，颗粒直径遵循正态分布规则，能够保证区域内颗粒填充密度与实际相符，建立内瓤模型如图2(c)所示。

(a) 外表皮模型生成规则表(部分)

(b) 秸秆外表皮仿真模型(左图为无茎节，右图为有茎节)

2) 设置粘结参数。在EDEM中，合理的粘结参数是保证仿真模型成功建立的重要前提，粘结参数数值过大，会导致模型发生“爆炸”，粘结参数数值过小，模型出现坍缩、变形和塌陷等不稳定现象，通过反复调试，观测生成的仿真模型的稳定性，最终确定了外表皮—外表皮、内瓤—内瓤和外表皮—内瓤的粘结参数，如表1所示。

表1 颗粒粘结参数设置Tab. 1 Particle bonding parameter settings

3) 固定颗粒运动状态为静止，在计算域内添加一个平面，设置为Virtual并创建颗粒工厂，生成颗粒数量为1，生成颗粒类型为Meta-particle，生成方向沿Z轴，生成外表皮模型后，在中心位置生成圆柱形颗粒工厂，生成方式为填充整个区域，构建秸秆式样完整模型如图2(d)所示。

1.3 仿真环境参数设置

为了提高仿真精确性，防止漏算，建立加载件模具的三维模型，划分网格后共计1 080个网格单元，导入EDEM软件中，加载件压缩速度为2 mm/s，与实际压缩试验条件一致。合适的时间步长是成功建立颗粒之间粘结键的关键参数，时间步长过大，颗粒运动误差计算结果精度差，导致粘结键生成失败，颗粒将脱粒粘结键向四周散开，从而影响模型精度；时间步长过小会增大运算总时长，仿真效率低，综合考虑计算精度和仿真效率，时间步长设置为瑞丽步长的5%。网格大小为颗粒半径的2.5倍，共计8 489 664个网格。国内外研究人员针对玉米秸秆与加载件的接触参数进行了大量工作，为本研究提供了充足的数据参考，各项材料属性参数[9, 12-14]设置如表2所示，玉米无茎节秸秆单轴压缩仿真试验和万能实验机试验如图3所示。

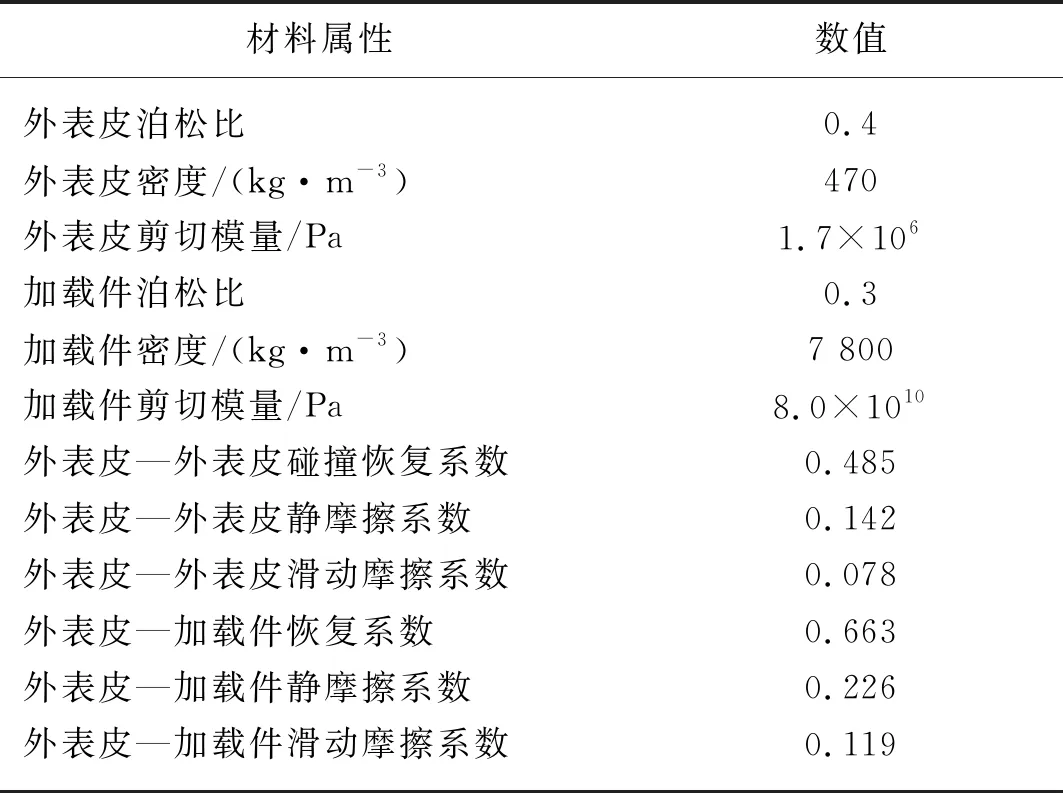
表2 材料属性参数设置Tab. 2 Material property parameter settings

(a) 仿真式样

(b) 压缩式样

1.4 Plackett-Burman仿真试验

Plackett-Burman试验能够在多个因素同时影响的条件下，选取每个因素的高低极限水平进行单因素试验，从而得到影响最为显著的因素[15-17]。本研究针对玉米秸秆外表皮和内瓤的仿真参数开展标定试验。需要标定的因素包括外表皮—内瓤碰撞恢复系数A、外表皮—内瓤静摩擦系数B、外表皮—内瓤滑动摩擦系数C、内瓤—内瓤碰撞恢复系数D、内瓤—内瓤静摩擦系数E和内瓤—内瓤滑动摩擦系数F共6个仿真参数进行筛选，试验水平如表3所示。仿真结束后和移除载荷后的玉米秸秆式样如图4所示。

表3 Plackett-Burman试验水平表Tab. 3 Plackett-Burman test level table

(a) 仿真式样

(b) 压缩式样

1.5 最陡爬坡仿真试验

由Plackett-Burman仿真试验结果可知，对玉米秸秆抗压力表现出显著影响的因素有外表皮—内瓤静摩擦系数、内瓤—内瓤碰撞恢复系数和内瓤—内瓤静摩擦系数。为了使上述3个试验因素水平快速逼近最优取值范围，开展最陡爬坡试验。

1.6 Box-Behnken正交试验

根据最陡爬坡仿真试验结果，以外表皮—内瓤静摩擦系数B、内瓤—内瓤碰撞恢复系数D和内瓤—内瓤静摩擦系数E3个参数为试验因素，以颗粒所受抗破坏力N为响应指标开展3因素3水平正交试验，共17组，探明上述3个试验因素对响应指标的影响规律，并进行最优参数优化[18-20]。

1.7 最优参数组合验证试验

根据正交试验结果，利用Design-Expert软件进行最优参数优化设计，设计规则如式(2)所示。为了验证仿真结果的准确性，将最优参数组合作为新的玉米秸秆仿真参数输入，分别进行剪切仿真试验和物理试验，对比相同参数组合下有茎节玉米秸秆式样的抗剪切力的大小，如图5所示。

(2)

图5 玉米秸秆剪切验证试验

2 结果与讨论

2.1 Plackett-Burman仿真试验结果

Plackett-Burman仿真试验结果如表4所示，方差分析结果如表5所示。该模型的P值为0.022 5<0.05，表明模型对颗粒抗破坏力的影响为极显著，因素B、D和E的P值<0.05，说明外表皮—内瓤静摩擦系数、内瓤—内瓤碰撞恢复系数和内瓤—内瓤静摩擦系数对颗粒抗破坏力的影响为极显著，而其他因素的影响均为不显著。

因此，将因素B、D和E作为最陡爬坡试验和Box-Behnken正交试验的变量，同时取外表皮—内瓤静摩擦系数A为0.5、外表皮—内瓤滑动摩擦系数C为0.055、内瓤—内瓤滑动摩擦系数F为0.055，均为其区间的中位数。

表5 Plackett-Burman试验分析结果Tab. 5 Plackett-Burman test analysis results

2.2 最陡爬坡仿真试验结果

最陡爬坡仿真试验结果如表6所示，第2组试验和第3组试验的颗粒抗破坏力分别为69.55 N和80.34 N，秸秆单轴压缩试验的抗破坏力为75.54 N，在第2组和第3组试验结果的区间范围内，因此将这两组试验因素的水平作为正交试验自变量因素的+1和-1水平。

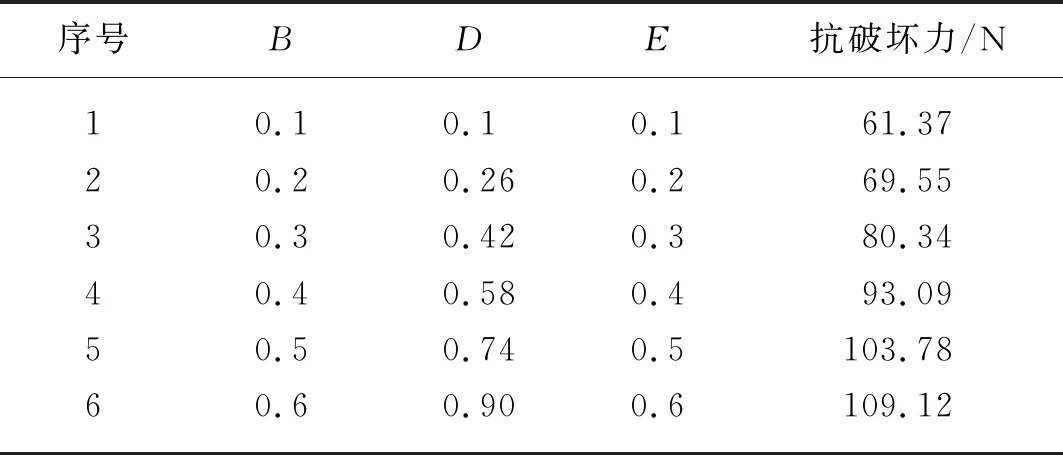
表6 最陡爬坡试验结果Tab. 6 Steepest climbing test results

2.3 Box-Behnken正交试验结果

为了获得显著影响因素(外表皮-内瓤静摩擦系数、内瓤-内瓤碰撞恢复系数和内瓤-内瓤静摩擦系数)的最优参数组合，正交试验安排表与颗粒抗破坏力结果如表7所示，方差分析结果如表8所示，得到变量的回归方程如式(3)所示。

F=-281.83+446.57B+895.38D+24.34E-

1 326.31BD+7.29BE+2.19DE+

259.73B2-716.43D2-1.44E2

(3)

由表8可知，因素拟合度为0.99，说明该模型具有较高的可信度，整个模型的P值<0.000 1，说明该模型的影响为极显著，能够可靠反映自变量与因变量之间的关系，模型失拟项的P值=0.475 8>0.10，说明该模型中不存在无关因素的影响。另外，自变量B、D和E的P值均小于0.05，说明选取的3个因素对颗粒抗破坏力的影响均为极显著，交互因素BD、二次项因素D2和E2的影响也均为极显著，其他项均为不显著。

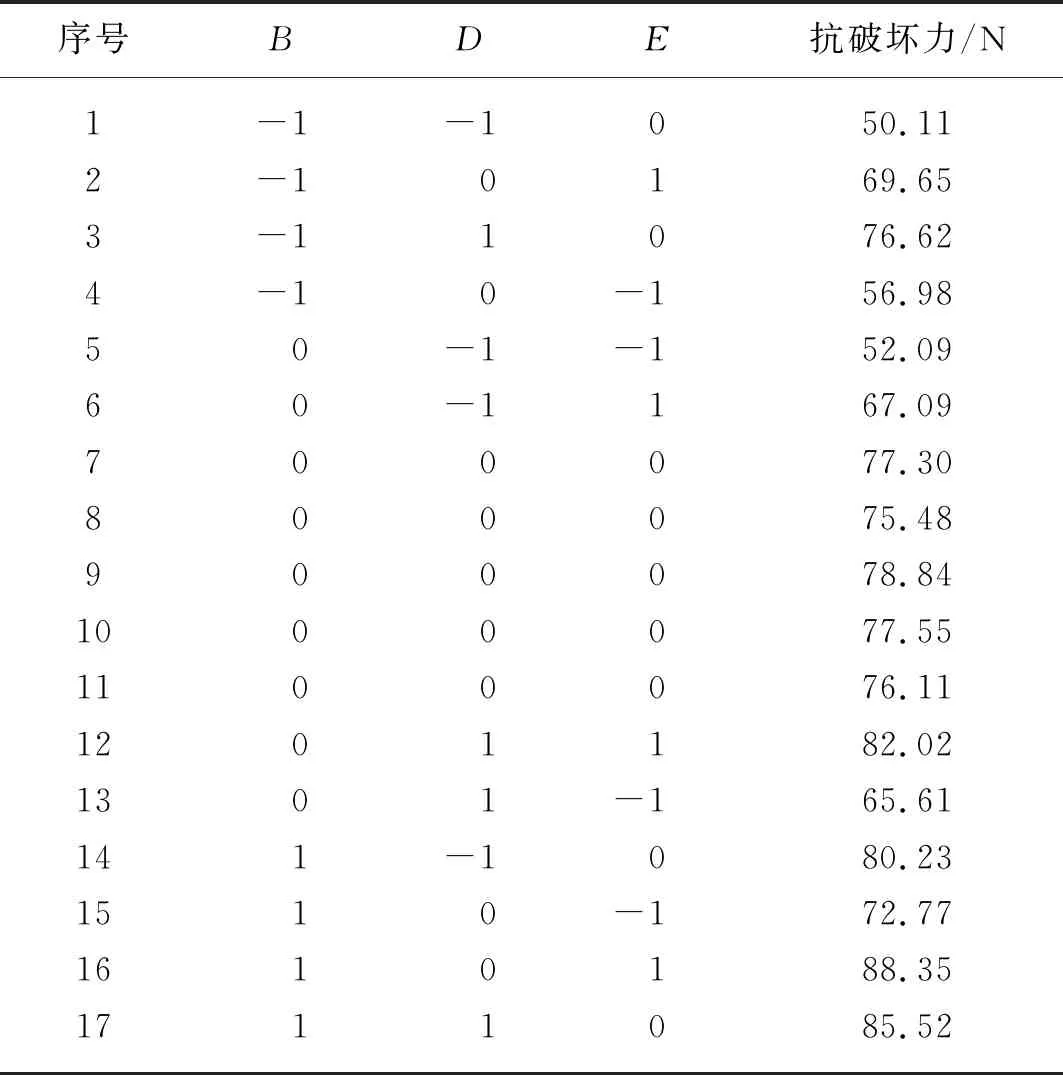
表7 正交试验安排与结果Tab. 7 Orthogonal test arrangement and results

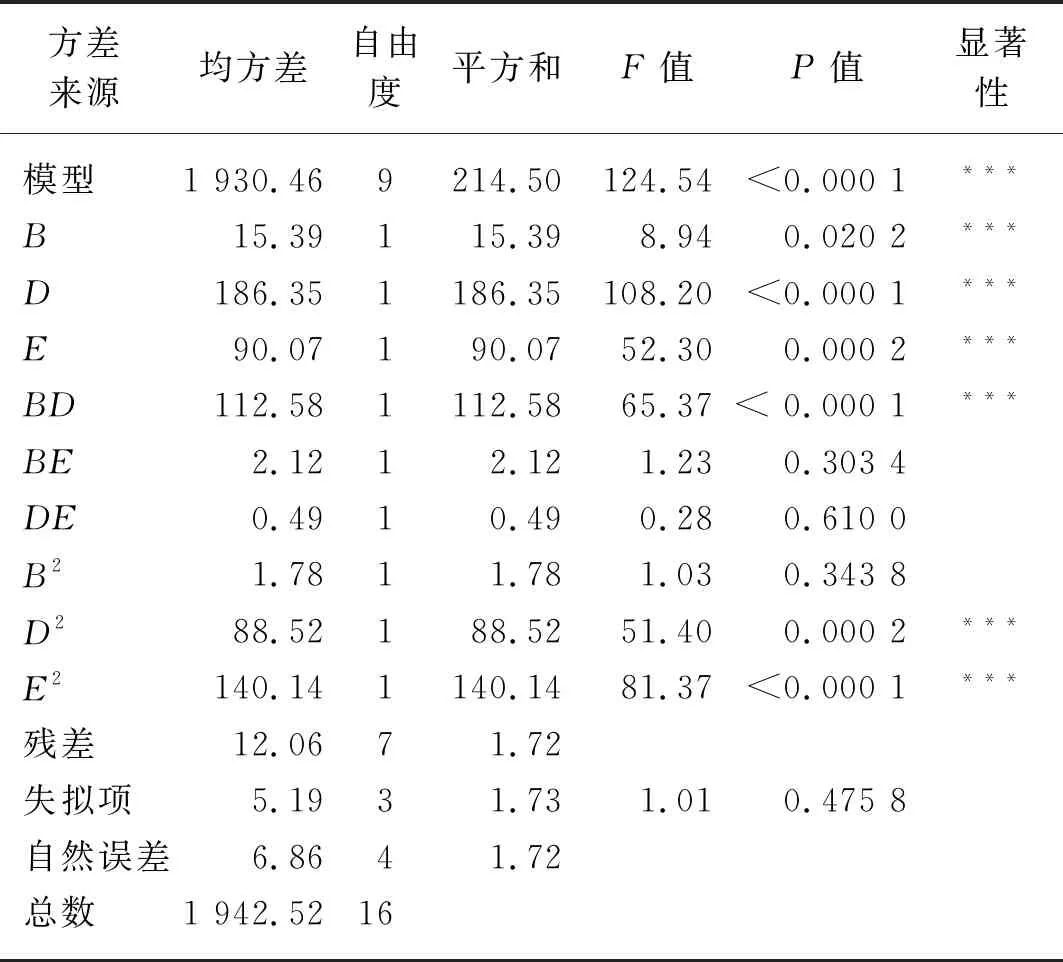
表8 正交试验方差分析结果Tab. 8 Results of ANOVA

剔除了影响不显著的因素后，各项显著性因素的影响程度次序为D、C2、BD、E、E2、B，根据模型的回归方程得到各自变量的交互作用对颗粒抗破坏力的响应面分析如图6所示。

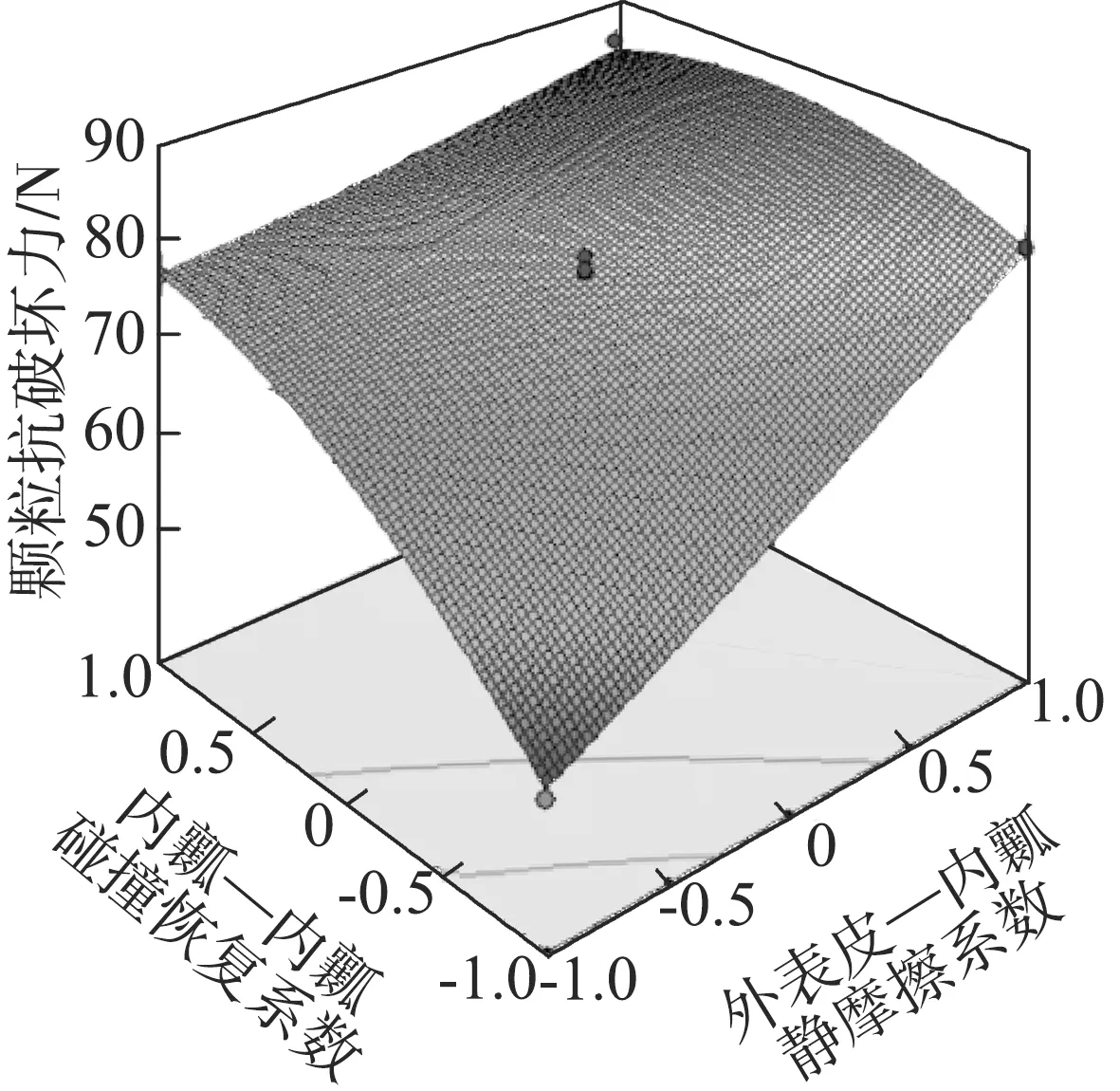
(a) F=(B,D,0)

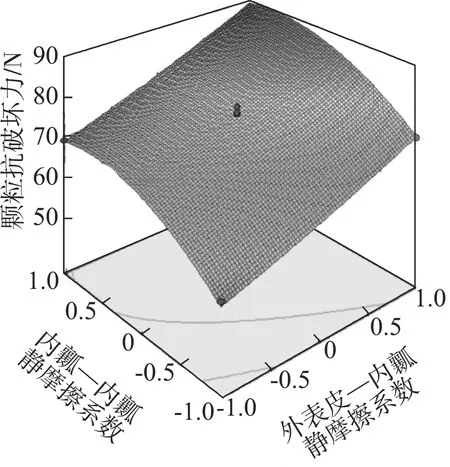
(b) F=(B, 0, E)

(c) F=(0, D, E)

由图6(a)可知，当外表皮—内瓤静摩擦系数为中间水平时，颗粒的抗破坏力随着内瓤—内瓤碰撞恢复系数的增大而平缓增大；当其处在低水平时，抗破坏力则随着内瓤—内瓤碰撞恢复系数的增大而迅速增大；当其处于高水平时，抗破坏力随着内瓤—内瓤碰撞恢复系数的增大先增大，后减小，变化幅度较为明显；由图6(b)可知，颗粒的抗破坏力随着外表皮—内瓤静摩擦系数和内瓤—内瓤静摩擦系数的增大而增大，变化幅度明显；由图6(c)可知，颗粒的抗破坏力随内瓤—内瓤碰撞恢复系数和内瓤—内瓤静摩擦系数的增大而增大，变化趋势明显，2个因素对抗破坏力的影响程度基本相同。

由式(3)得到实现抗破坏力最小值的参数组合为外表皮—内瓤静摩擦系数0.28、内瓤—内瓤碰撞恢复系数0.29、内瓤—内瓤静摩擦系数0.23，此时加载件受力为76 N，与目标值误差为0.46 N。

2.4 验证试验

根据最优仿真参数组合进行仿真试验，并随机取玉米有茎节秸秆在万能实验机进行剪切试验的5组抗破坏力曲线与仿真试验中颗粒抗破坏力曲线进行对比，结果如图7所示。玉米有茎节秸秆离散元模型在验证试验中的抗破坏力为132.29 N，在物理试验中抗破坏力平均值为131.36 N，相对误差仅为0.93 N，说明仿真试验结果与物理试验结果基本一致，验证了玉米秸秆精细化离散元仿真模型的可靠性与准确性。

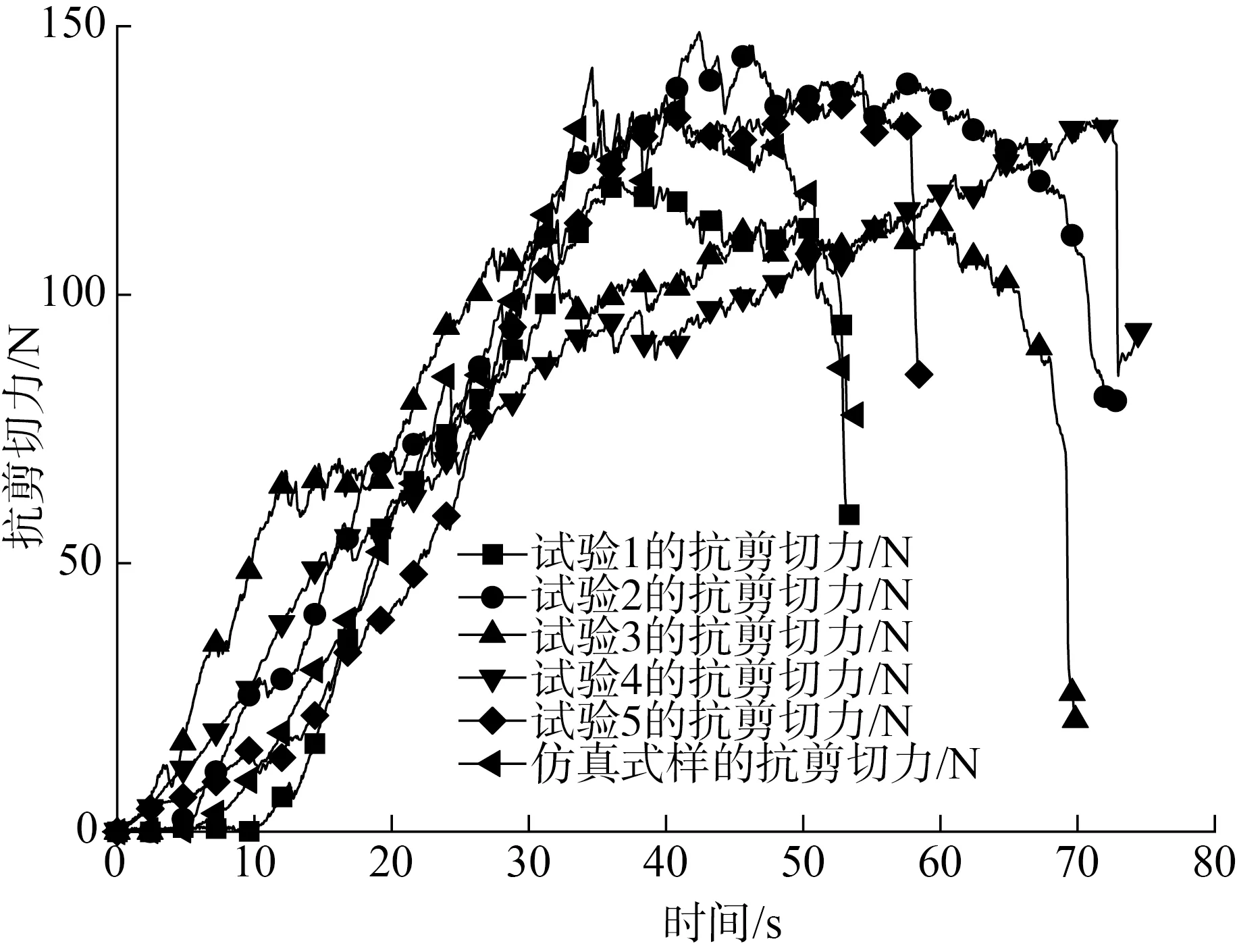
图7 玉米有茎节秸秆剪切验证试验对比结果

3 结论

针对玉米秸秆外表皮与内瓤存在较大差异，导致离散元仿真模型精确性不足的问题，提出了一种玉米无茎节和有茎节秸秆的精细化离散元仿真模型的建立方法，探究了该模型下的仿真参数最优组合。

1) 万能实验机物理试验测得玉米无茎节秸秆的单轴压缩抗破坏力为75.54 N，为了获得与实际值相近的仿真参数，利用Plackett-Burman试验和Box-Behnken回归正交试验开展6个参数的仿真试验，结果表明对抗破坏力具有显著影响的因素包括外表皮—内瓤滑动摩擦系数、内瓤—内瓤碰撞恢复系数和内瓤—内瓤静摩擦系数。

2) 根据方差分析结果，进行最优参数优化，得到满足要求的参数组合为外表皮—内瓤静摩擦系数0.28、内瓤—内瓤碰撞恢复系数0.29、内瓤—内瓤静摩擦系数0.23，此时颗粒抗破坏力的预测值为76 N，与实际值75.54 N的误差为0.46 N。

3) 建立玉米有茎节秸秆离散元精细化仿真模型，利用最优参数组合开展剪切验证试验，仿真试验与物理试验的抗剪切力分别为132.29 N和131.36 N，误差仅为0.93 N，表明本文提出的离散元仿真模型建立方法和仿真结果可靠有效，能够为其他作物离散元仿真研究提供参考。