四轮轮毂电机驱动农用无人车差速转向建模与分析*
杜雄梓,周亢,雷帅帅
(北京理工大学机电学院,北京市,100081)
0 引言
四轮轮毂电机驱动差速转向式无人地面车辆由于取消了传统车辆的动力传动及转向机构,优化了车辆的空间布局,有利于装备的轻简化,在农业领域有着广泛的应用前景[1-2]。轮式差速转向车辆不依靠车轮偏转而是通过控制两侧车轮产生速度差来实现转向,在各种地形上都有良好的机动性[3]。但是在转向过程中,由于轮胎与地面之间的复杂接触以及车轮之间的相互制约,会使车辆产生滑移现象,这是在对相关车辆差速转向机理的研究中不可忽视的问题[4]。
国内外学者对差速转向机理的研究多针对履带式车辆[5-6],对于轮式车辆差速转向机理的研究大多是针对六轮及以上的装甲车辆[7-8],对四轮驱动差速转向模式的研究也往往仅针对60 kg以下的轻小型的车辆[9-11]。由于驱动形式、转向灵活性、车体尺寸的不同,这些研究的方法及结论不太适用于指导大型四轮驱动车辆的差速转向及航路推算[12]。
本文针对一种大型四轮阵列式轮毂电机驱动农用无人车,对其差速转向滑移机理展开研究。基于大半径转弯及转弯中心不变理论,建立其理想状态下的差速转向二自由度运动学模型,得到转弯半径与内外侧车轮处真实速度差之间的关系。但考虑到对大型四轮驱动车辆的精准路径规划不能只依赖于理想模型,还需要对整车的行驶状态进行精确测量,本文在实车试验时采用高精度传感器及组合导航系统实时测量车辆转向时的运动参数[13],分析得到两侧车轮转速差与两侧车轮处真实速度差之间的拟合方程,并引入误差系数对模型进行了修正。本文内容将有助于加深对该类车辆滑移特性的理解,进而进一步服务于各种学术研究或实际工程应用。
1 四轮阵列式轮毂电机驱动无人车结构
车架采用双层铝型材结构,可加装不同的任务载荷,来完成农产品运输及植保无人机发射等任务。整车质量为300 kg,左右轮距为1.45 m,前后轴距为1.6 m,配备有完备的动力系统、液压制动系统、电源管理系统、弹簧减振悬架系统以及能够实现车辆实时运行状态反馈的整车控制系统。为了实现大功率运行,每个轮毂上安装了五个直流电机和一个液压制动器,相应的结构如图1所示。

(a) 动力系统实物图
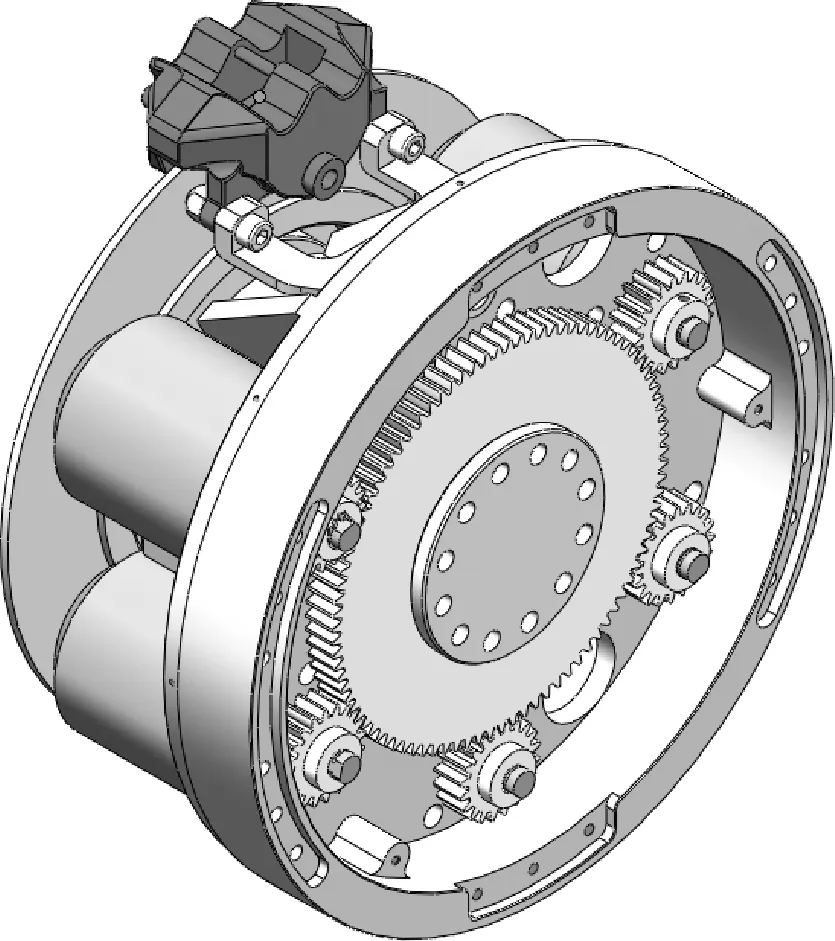
(b) 动力系统示意图
在运动过程中,通过采集电机内部霍尔传感器的信号频率,可以实时测量每个车轮电机的转动速度[14]。结合齿轮传动比和车轮半径等固有参数,可以准确地计算得到每个车轮的实时转速。
2 建立差速转向运动学模型
2.1 模型假设
以上述四轮阵列式轮毂电机驱动农用无人车为研究对象,建立车辆的差速转向运动学模型,该模型基于以下前提假设:忽略车辆行驶过程中的垂直平动、俯仰和侧倾运动;假设质心位于车辆几何中心;车辆运动坐标系与质心重合[15];假设车辆自身旋转中心在车辆质心前方位置处[16];假设车辆为一刚体,不考虑轮胎及悬架作用;假设车辆进行大半径转弯,即车辆的转弯半径远大于车辆宽度;以车辆向前行驶左转弯为例展开分析,即右轮速度大于左轮速度,此时右轮为外侧车轮,左轮为内侧车轮。
2.2 运动学模型
整车的运动学模型如图2所示。xoy坐标系为车身坐标系,其中x指向车辆前进方向;O为车辆转弯中心,O1为车辆自身旋转中心,CG为车辆的质心;u和v分别为车辆质心沿x、y轴方向的前向和侧向速度;ω为车辆质心CG绕自身旋转中心O1的转动角速度,其等于车辆绕转弯中心转动的角速度;R0为O1到O的距离,即车辆转弯半径的大小;L为车辆前后轴距,B为左右轮距,D为转弯中心O1相对于车辆质心CG的偏移量;β为车辆质心相对于转弯中心O旋转的角度;α为车轮相对于转弯中心O旋转的角度(车轮转向角),V表示车轮处转向时的真实速度,其中下标i表示内侧车轮,o表示外侧车轮,1表示前轴车轮,2表示后轴车轮,x表示沿x轴方向的速度,y表示沿y轴方向的速度;车轮处u表示车轮沿x轴和y轴方向速度的合速度。
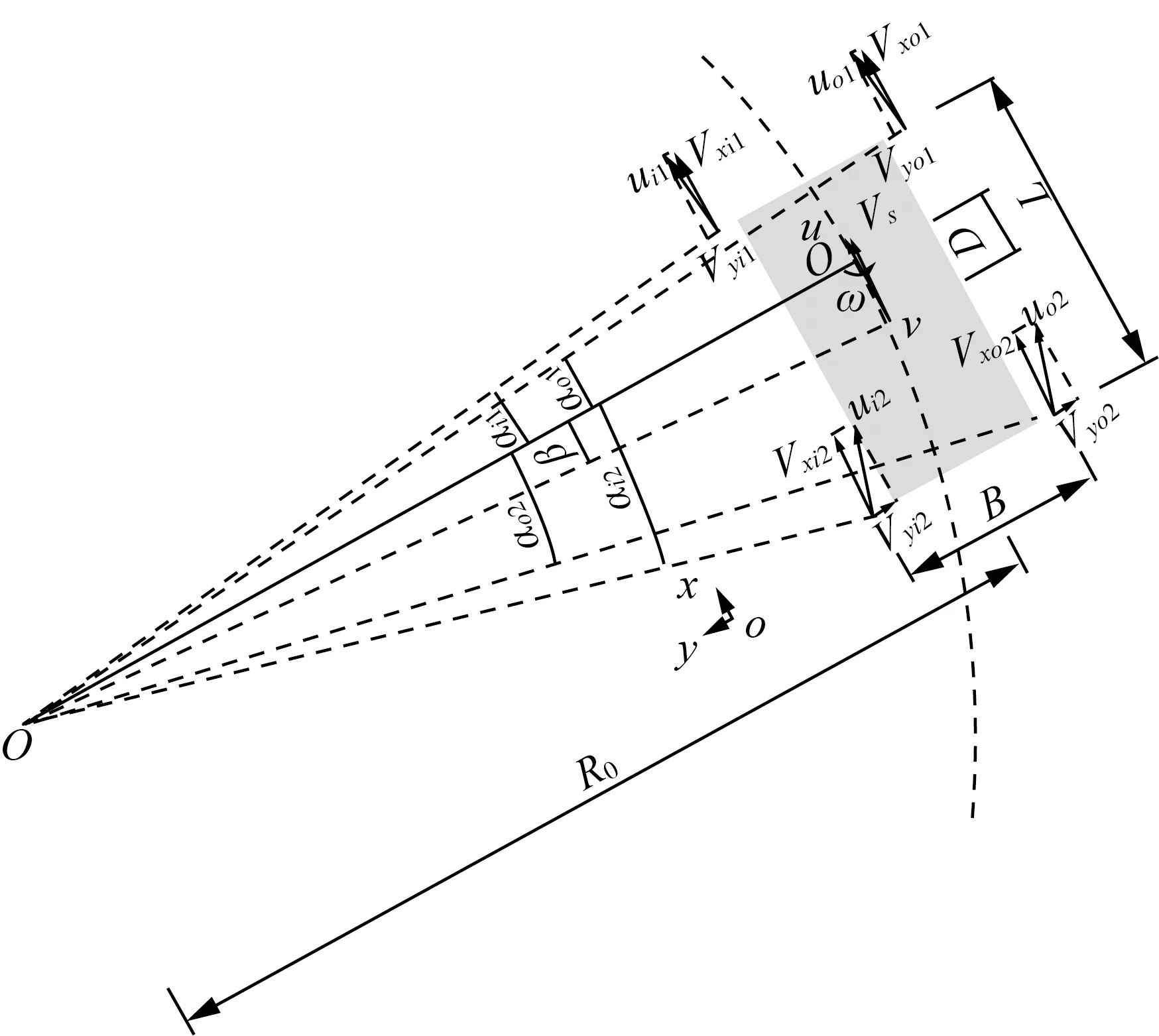
图2 整车运动学模型
由图2可知,β及α满足以下几何关系。
(1)
由于四轮及质心绕车辆自身旋转中心O1的转动角速度相等,都为ω。因此前轴两车轮沿y轴方向的速度相等,后轴两车轮沿y轴方向的速度相等。结合式(2)前向速度u与侧向速度v之间的几何关系,计算得到四轮沿y轴方向速度,如式(3)所示。
(2)
(3)
四轮沿x轴方向的速度Vx可由四车相对于转弯中心旋转的角度α与Vx和Vy之间的几何关系得到,如式(4)所示,分析可知转弯中心的偏移量D不会对Vx的计算产生影响。
(4)
计算内外两侧车轮处沿x轴方向的真实速度Vx之间的差值(由ΔVx表示),如式(5)所示。
(5)
由式(5)变换可得,车辆质心处的前向速度u、车轮处沿x轴方向真实速度差ΔVx与转弯半径R0之间的关系,如式(6)所示。
(6)
由式(6)可知,已知车辆运行时ΔVx与u的值,即可计算出转弯半径R0的大小。在实际的大半径差速转向过程中,ΔVx的值远小于车辆的前进速度u,其微小的误差就可导致R0的计算不准确,因此要准确计算出转弯半径R0的大小,需要精准控制及测量计算出内外两侧车轮处沿x轴方向真实速度差ΔVx的大小,这是差速转向路径规划的关键,也是本文进行差速转向实车试验的最终目的。
另外,转弯中心相对于车辆质心的偏移量D会对四轮各自的转弯半径(即车轮到转弯中心的距离)产生影响[17]。二者之间的关系如式(7)所示。
(7)
由于转弯中心偏移量D的最大值为L/2,当车辆大半径转弯时,转弯半径R0远大于D,由式(7)可知,此时D对四轮各自转弯半径的影响很小,因此在后续试验中忽略不计D对转弯半径R0的影响。
3 差速转向实车试验
大型四轮驱动车辆在差速转向时轮胎与地面之间的接触及受力情况复杂,四轮各自位置相对于车体固定,并且四轮独立驱动的形式使得在行驶过程中各车轮之间的运动会相互制约,导致车辆产生滑移现象,使内外两侧车轮转速与内外两侧车轮处的真实速度存在一定偏差。在车辆行驶过程中,车轮转速往往比较容易获取,但由于滑移现象的存在,若直接按内外两侧车轮转速差计算ΔVx,并代入式(6)中计算转弯半径R0,会导致计算结果与实际转弯半径出现较大误差。为探究车轮转速差与车轮处真实速度差之间的关系,基于自主研制的四轮轮毂电机驱动农用无人车设计完成以下实车试验。
3.1 测试系统搭建
测试系统的组成及布置如图3所示。

图3 测试系统组成及布置
安装在驱动电机内的霍尔传感器用于测量四轮的实时转速;高精度光纤捷联惯导系统安装在车辆的质心位置,与差分式北斗共同组成车辆的组合导航系统,能够提供车辆的实时经纬度坐标信息(误差为厘米级),并且能够准确测量车辆的行进速度以及俯仰、滚转和偏航角度[18];车载控制系统采用ARM处理器,负责控制车辆的运动状态,并将各传感器采集到的数据反馈至计算机进行记录[19]。
3.2 差速转向测试
控制车辆运行的目标轨迹示意图如图4所示。首先控制车辆进行直线行进加速,此时内外侧车轮转速相等,待车速达到5 m/s并运行平稳后,控制内外侧车轮以设定的转速差进行转向,此时外侧车轮转速大于内侧车轮转速,车辆行驶路径为圆弧。改变车轮转速差的设定值进行多组试验。
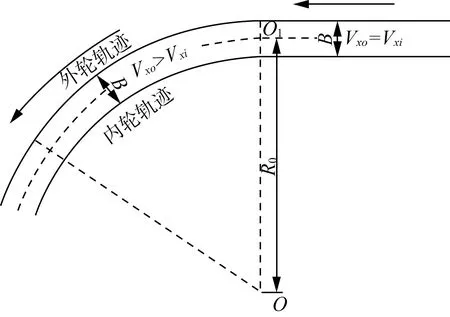
图4 运行轨迹示意图
组合导航系统监测到车辆运行的轨迹如图5所示。车辆先直行后转向,与目标运行轨迹相符。

图5 车辆运行轨迹卫星图
3.3 数据分析处理
以转弯半径为64 m实车试验为例,霍尔传感器及光纤捷联惯导监测到试验过程中车辆运行速度如图6所示。惯导测量质心处的前向速度u,外轮均速和内轮均速分别为外侧两车轮和内侧两车轮的平均转速(在后续计算中以Δn表示内外轮均速之差)。
光纤捷联惯导监测到试验过程中车辆航向角的变化曲线如图7所示(选取3组数据进行展示)。
分析图6和图7数据可知,在0~8 s内车辆由静止开始加速直至匀速行驶,车辆的偏航角度变化小于1°,直线行驶平稳;在8 s后的差速转向阶段,内外轮转速稳定,转速差基本恒定,车辆偏航角度近似呈线性变化。结合车辆运行轨迹卫星图5,可认为车辆在差速转向阶段运行轨迹为圆弧形,转弯中心为一固定点。
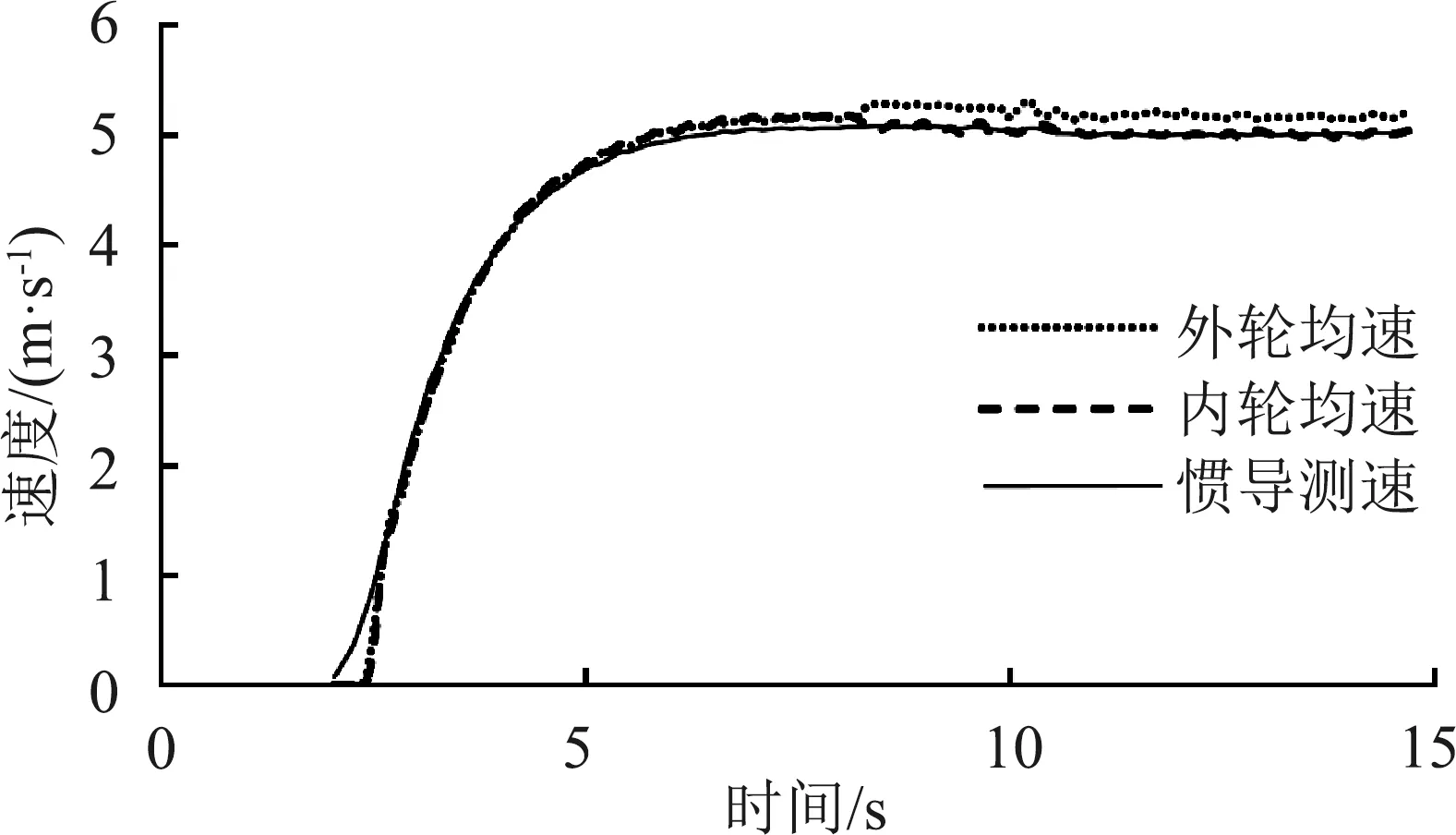
图6 车辆运行速度曲线
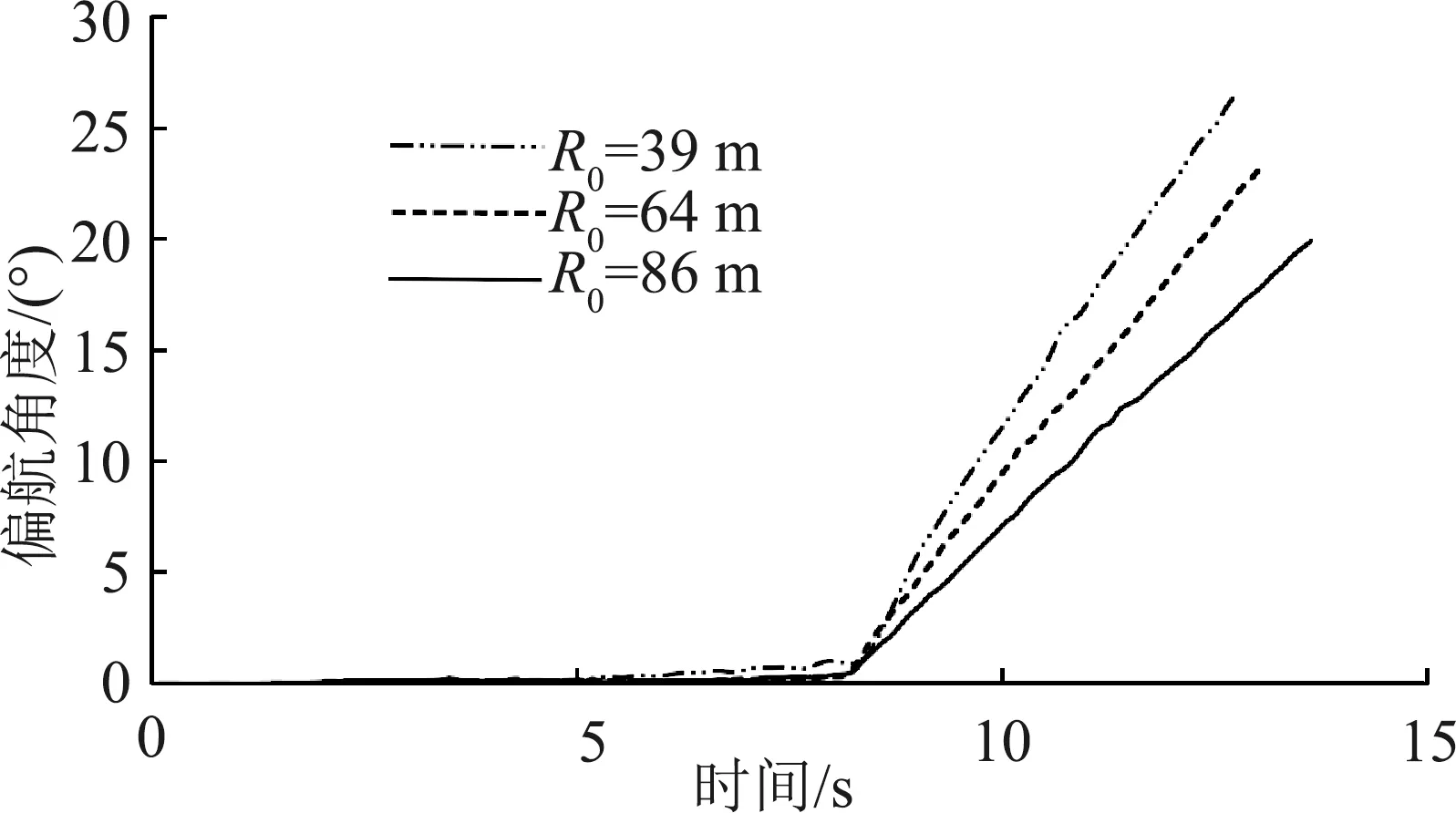
图7 偏航角度变化曲线图
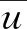
(8)
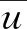

表1 试验计算结果Tab. 1 Calculation results of the experiment
由表1可知,在差速转向过程中,车轮产生的滑移现象导致内外侧车轮的转速差Δn始终比内外侧车轮处的真实速度差ΔVx偏大。结合多组试验数据对Δn与ΔVx进行拟合,结果如图8和式(9)所示,可以看出二者呈明显的线性关系。

图8 Δn与ΔVx之间的拟合关系
ΔV=0.526Δn+0.027 61
(9)
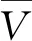
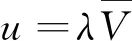
(10)
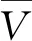
(11)
将由式(11)计算出的转弯半径与由式(8)计算出的标准转弯半径相比较,结果如表2所示。
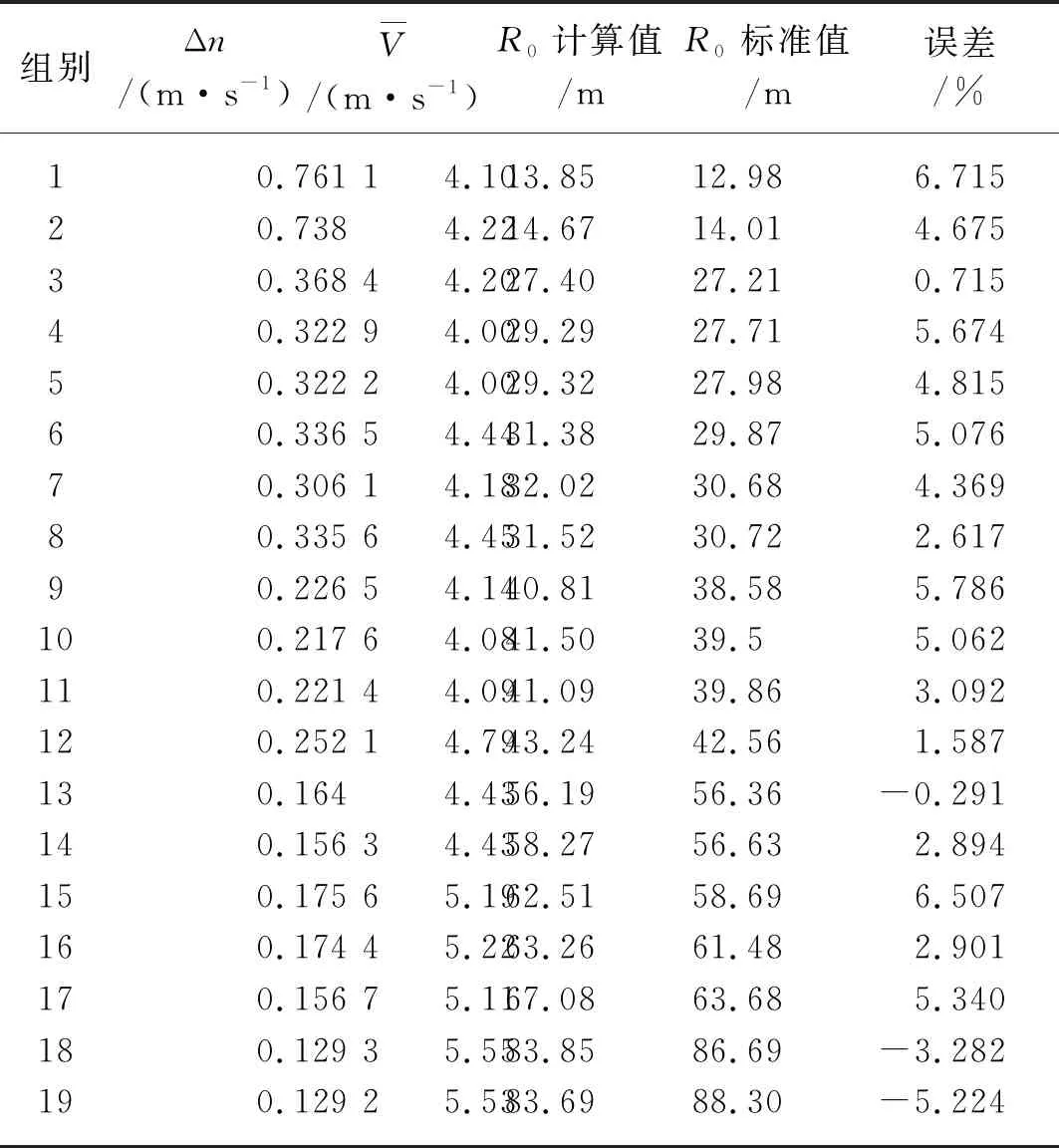
表2 试验数据表Tab. 2 Experimental data sheet
修正后的差速转向运动学模型仅通过四轮转速的测量值就可计算出车辆的转弯半径大小,并且与标准转弯半径相比,平均绝对误差为4.033%,最大误差为6.715%,且分布无明显规律,说明模型计算结果的准确度较高,误差最大值在转弯半径为12.98 m时出现。
4 结论
基于大半径转弯前提,考虑了无人车的一些重要几何参数和运动特性,建立了四轮无人车的二自由度差速转向运动学模型,分析了车辆运行速度及内外侧车轮处真实速度的差值与转弯半径之间的关系,以及转弯中心偏移量对转弯半径的影响。基于高精度的传感测试系统,设计完成了四轮轮毂电机驱动农用无人车的差速转向试验,得到了内外侧车轮转速差与车轮处真实速度差之间的拟合方程,并对建立的运动学模型进行修正。依据修正后的模型,可不依赖昂贵的导航系统,仅通过对四轮转速的测量就可计算出车辆实时转弯半径的大小,平均绝对误差为4.033%,最大误差为6.715%,可为类似农用无人车的差速转向及航路推算提供理论依据及试验指导。

