永磁同步电机长线变频驱动系统定频滑模预测电流控制

郑长明 阳佳峰 高 昂 公 铮 伍小杰

（1.中国矿业大学电气工程学院 徐州 221116 2.国网江苏省电力有限公司镇江供电分公司 镇江 212002）

0 引言

随着我国“2030 碳达峰、2060 碳中和”战略目标的提出，加快推进煤炭高效开发与节能降耗迎来了新的挑战。常见的煤矿生产运输装备（如带式、刮板运输机等）核心部件为矿用电机，其传统驱动系统多为交流异步电动机变频驱动并配有减速器，存在维护费用高、功率因数和效率低等缺点。永磁同步电机（Permanent Magnet Synchronous Motor,PMSM）变频直驱系统，具有结构紧凑、高效率和高可靠性等优点，近年来在煤矿工业受到了广泛关注[1]。特别是在煤矿井下开采运输应用场合，考虑到工作空间、隔爆和散热问题，优选采用井下电机、井上集中变频驱动方式。然而，其间连接的长线缆产生了诸多负面影响：①加剧机端尖峰过电压；②加快电机绕组和轴承绝缘老化；③增大谐波损耗和转矩脉动等[2]。一种较为理想的解决方案是在逆变器侧加装LC 滤波器[3]。但该方法增大了系统控制阶数，导致传统控制策略无法适用。现有线性控制器通过增加LC 滤波控制环以保证系统稳定性，但造成了级联环路多和参数整定复杂等问题，降低了煤矿生产可靠性[4]。因此，亟须探索高性能PMSM长线变频驱动控制策略。

非线性控制策略被认为是解决多变量、强耦合PMSM 驱动系统高性能控制的一种有效方案。其中，模型预测控制（Model Predictive Control,MPC），以其概念直观、多目标优化和约束处理灵活等优点在PMSM 驱动领域中应用广泛[5-7]。MPC 的基本原理是借助系统离散模型，通过最小化价值函数以获得最优控制量，并应用于变换器以预测系统未来状态。为不断优化控制性能，目前PMSM 驱动系统预测控制已从传统单矢量MPC 发展到多矢量MPC。单矢量MPC，即在控制周期内直接作用单一电压矢量，故动态响应较快[5]。但其因缺失调制级而造成输出纹波大、开关频率不固定等问题，无法满足高精度控制要求。因此，多矢量MPC 应运而生，其主要包括：双矢量、三矢量和虚拟矢量MPC[8-13]。文献[9]通过同时作用一个非零矢量和一个零矢量，提出了基于占空比优化的双矢量 MPC，改善了单矢量MPC 稳态性能，并实现了准恒定开关频率。文献[10]将上述双矢量MPC 的候选矢量扩展为任意矢量，提出了一种改进双矢量MPC，进一步优化了系统稳态性能。文献[11]采用相邻两个非零矢量和一个零矢量共同作用，提出了一种三矢量MPC 策略。该控制方法在实现固定开关频率的同时，大大降低了稳态输出纹波。文献[12]提出了一种虚拟矢量MPC，通过基本电压矢量合成虚拟矢量以提升控制精度，但一定程度上增加了计算量。此外，考虑到价值函数直接决定最优控制量的选择，故通过改进价值函数亦可优化系统控制性能。文献[13]将PMSM 电流跟踪误差积分项加入到价值函数中，有效降低了电流稳态跟踪误差。

尽管如此，现有MPC 策略大多针对无输出LC滤波器PMSM 驱动系统设计。目前，国内外针对带LC 滤波器PMSM 长线驱动系统预测控制的报道不多[14-16]。文献[14]提出了LC 滤波型PMSM 驱动系统的传统单矢量MPC 策略，但其仅考虑定子电流优化而忽略了LC 滤波器特性，且各控制周期采用单一电压矢量，故导致系统稳态精度和稳定性差。文献[15]提出了长时域单矢量MPC，一定程度上提升了系统稳态性能，但其计算量较大、对硬件要求较高。而且，上述MPC 策略均非恒定开关频率，这将不利于LC 滤波器的设计，容易激发不期望的谐振动态[16]。此外，注意到滑模控制可强制驱使系统状态到达滑模面，从而提高系统抗扰能力[17]。因此，若将滑模思想融入到MPC 设计中，则有望发挥二者优点以进一步提升控制性能。

为此，本文提出了一种PMSM 长线变频驱动系统定频滑模预测电流控制（Fixed Switching Frequency Sliding-mode Predictive Current Control,FSF-SPCC）。首先，借助滑模切换函数建立了离散滑模预测模型，并设计了一种基于滑模面跟踪的新型价值函数。其次，提出了一种三矢量定频 FSFSPCC 策略，其具有固定开关频率，可方便输出LC滤波器的设计，并可减小PMSM 定子电流的稳态纹波。最后，通过实验验证了所提控制方案的可行性。

1 PMSM 长线变频驱动系统建模

1.1 PMSM 长线变频驱动系统离散模型

带输出LC 滤波器的两电平三相电压源逆变器供电PMSM 长线变频驱动系统结构如图1 所示。图中，Lf、Cf为输出滤波电感和电容；if、vf、v和is分别为滤波电感电流、滤波电容电压、逆变器输出电压和PMSM 定子电流矢量，ωe为PMSM 电磁角速度，Vdc为直流侧母线电压，Sa、Sb、Sc分别为逆变器三相上桥臂开关状态。

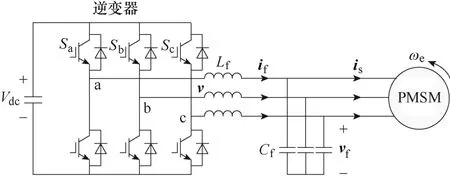
图1 PMSM 长线变频驱动系统结构Fig.1 Structure chart of a PMSM long-cable variable frequency drive system

根据图1 所示，可以建立带输出LC 滤波器的PMSM 长线变频驱动系统在连续时间域下的状态空间方程为

式中，x为状态矩阵；下标d、q 为dq 旋转坐标系变量；Rs、Ls和ψf分别为表贴式PMSM 定子电阻、定子电感和转子磁链。if、vf和is可通过测量或观测得到[3]；v可由其αβ 坐标系值经过如下变换求得

式中，θ为PMSM 转子电角度；vα、vβ分别为逆变器在α、β 坐标系下电压，逆变器电压矢量与开关状态见表1。

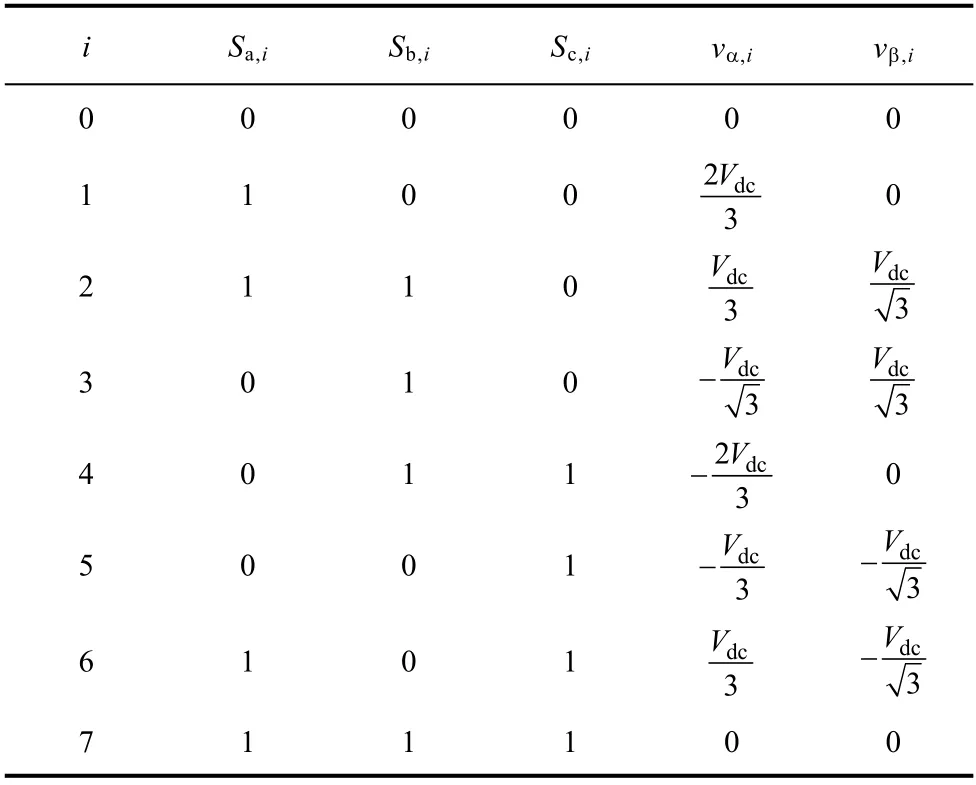
表1 逆变器电压矢量与开关状态Tab.1 Inverter voltage vectors and switching states

进一步地，假设系统采样时间为Ts，在kTs时刻采用零阶保持器对式（1）进行精确离散化，可得到PMSM 长线变频驱动系统的离散状态空间模型为

式中，τ为积分变量。

1.2 PMSM 长线变频驱动系统谐振机理

基于式（1），忽略PMSM 电压方程中dq 轴间的交叉耦合项，可得到逆变器、输出LC 滤波器和PMSM 构成的长线变频驱动系统dq 轴等效电路，如图2 所示。

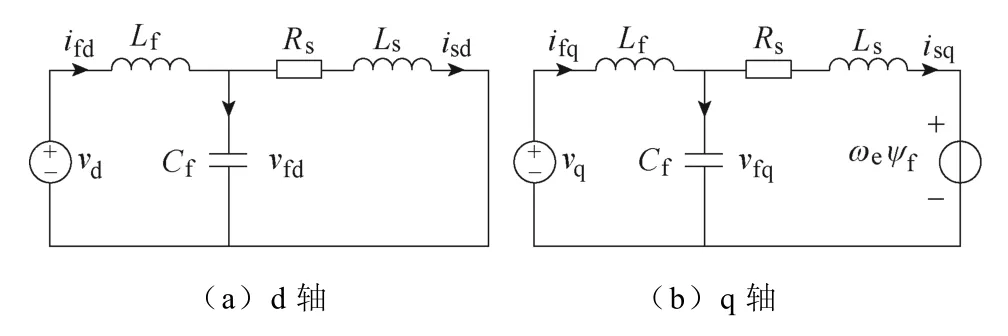
图2 PMSM 长线变频驱动系统dq 轴等效电路Fig.2 dq axis equivalent circuit of a PMSM long-cable drive system

由图2 可知，PMSM 长线变频驱动系统等效电路具有类似于LCL 滤波器的结构。这种LCL 滤波网络可能产生谐振问题，从而影响系统稳定性。具体来说，其产生的谐振频率fres为

因此，在设计PMSM 长线驱动系统控制策略的同时，需考虑对此类LCL 谐振特性进行抑制。

2 传统PMSM 长线驱动系统MPC

常规 PMSM 长线驱动系统预测电流控制的主要目标是基于内环电流id=0 的矢量控制框架，采用单矢量MPC 实现对定子电流的高性能跟踪控制。为实现上述目标，其价值函数通常设计[14]为

式中，为q 轴定子电流参考值，由转速外环生成；isd,k+1和isq,k+1分别为第k+1 步d、q 轴定子电流预测值，由系统离散模型式（3）获得。

将表1 中8 个基本电压矢量依次代入到价值函数式（5）中进行评估，最终选取能够最小化价值函数的最优电压矢量（开关状态）直接作用于逆变器。由此可以看出，传统单矢量MPC 缺少了调制级，故开关频率不固定，不利于输出滤波器的设计。此外，其价值函数忽略了输出LC 滤波器特性，故无法保证系统的稳态性能和谐振稳定性。

3 新型定频FSF-SPCC

为了进一步提升 PMSM 长线变频驱动系统传统预测电流控制的输出性能，并方便输出LC 滤波器的设计，本节将滑模控制理论引入到MPC 的设计过程中，提出了一种新型三矢量定频滑模预测电流控制策略。

3.1 离散滑模预测模型构建

考虑到带输出LC 滤波器的PMSM 长线变频驱动系统主要控制目标是定子电流高性能跟踪控制，结合滑模控制原理，首先设计基于定子电流跟踪的线性滑模切换函数为

式中，s=sd+jsq为滑模切换函数复矢量；is=isd+jisq、分别为d、q 轴定子电流反馈及其参考复矢量；λ＞0 为滑模切换增益/权重因子；ψs=ψsd+jψsq=Lsis+ψf为定子磁链复矢量。

进一步地，结合式（3）和式（6），可推导出基于滑模切换函数的离散预测模型为

式中，is,k+1、vf,k+1和ψs,k+1=Lsis,k+1+ψf可直接由式（3）获得。因机械时间常数比电磁时间常数大得多，故PMSM 转速被认为在一个Ts内保持不变，即有ωe,k+1=ωe,k。

3.2 基于滑模面的价值函数定义

滑模控制的本质是驱使切换函数到达并维持在滑模面s=0 上或其附近的邻域内，从而保证系统状态对模型参数失配和外部扰动的鲁棒性。基于此，为了保证系统状态最优地到达滑模面，本文设计了如下基于“等效控制”的新型滑模价值函数为

式中，s*为滑模切换函数参考（即滑模面）复矢量，故有如下关系

从式（7）和式（8）可看出，所提出基于滑模面跟踪的价值函数内在地实现了多状态变量控制（即定子电流is和滤波电容电压vf）。同时，考虑到Lf和Cf连接节点处存在基尔霍夫电流定律约束，故所提方法能够有效抑制LCL 无源器件的谐振能量振荡，从而实现固有谐振阻尼。

3.3 三矢量定频FSF-SPCC 设计

首先，为了降低计算负担，采用基于电压矢量的预测模型代替式（7）中所提基于滑模切换函数的预测模型，以消除切换函数在预测过程中的计算量。具体而言，根据无差拍预测控制原理，假设滑模切换函数在第k+1 步到达滑模面，即：令式（7）中sk+1=0。为了简单，忽略定子电阻Rs，可求得滑模参考电压矢量的矩阵形式为

基于此，可推导出基于电压矢量的滑模价值函数为

式中，gi为表1 中第i个电压矢量对应的价值函数；分别为α、β 坐标系下的滑模参考电压，其可由式（10）经过以下变换求得

对比式（8）和式（11）可知，基于电压矢量预测模型的滑模价值函数仅需进行1 次参考电压矢量计算，而无需在评估gi时对切换函数sk+1进行多次预测，一定程度上降低了计算量。

其次，为了实现恒定开关频率，参照空间矢量调制（Space Vector Modulation,SVM）的基本原理，逆变器基本电压矢量及扇区分布如图3 所示，在每个开关周期选取扇区中相邻两个非零矢量vx、vy和零矢量v0/v7以合成式（10）中的滑模参考电压矢量v＊。其中，不同扇区下的候选非零矢量组合vx、vy见表2。

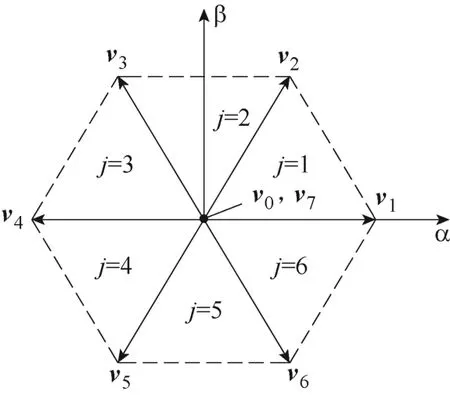
图3 逆变器基本电压矢量及扇区分布Fig.3 Space vector and sector distribution of an inverter

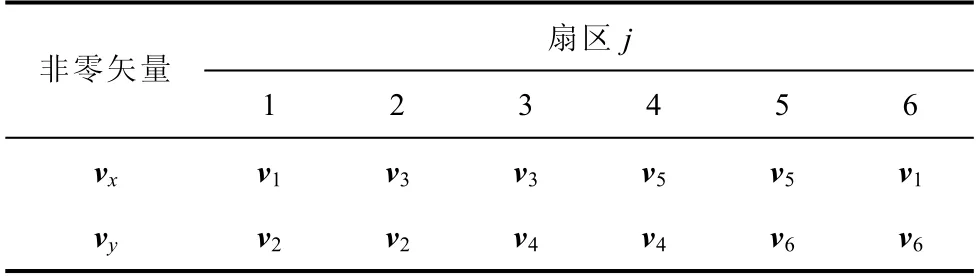
表2 各扇区候选非零矢量组合Tab.2 Candidate non-zero vector group of each sector

进一步地，需要计算出各候选电压矢量作用的占空比。设dx、dy、d0分别为矢量vx、vy、v0/v7对应的占空比，其可根据占空比与相应价值函数值的反比关系[18]求得

式中，gx、gy和g0为分别将vx、vy、v0/v7代入式（11）计算出的价值函数值；K为正常数，其可根据gx、gy和g0求得

最后，需要确定能够使得滑模参考电压矢量v＊与候选电压矢量间加权跟踪误差最小化的扇区jop。为此，重新定义以下价值函数Gj为

式中，j为扇区号。

因此，通过遍历6 个扇区以评估式（15），最终可选择出能够最小化Gj的最优扇区jop，并将其对应的最优电压矢量组合vx,op、vy,op、v0/v7与占空比dx,op、dy,op、d0,op利用7 段式SVM 对称发波原理生成脉宽调制波，即可实现固定开关频率[16]。

3.4 延迟补偿

注意到MPC 在实际数字实现时存在一步控制延迟，若不对其补偿则将影响系统性能。为此，本文采用基于“两步向前预测法”进行控制延迟补偿[19]。基于式（3），首先利用第k步时确定的最优矢量预测出第k+1 步的系统状态xk+1；然后将式（10）中的xk替换为xk+1即可。

本文所提出的PMSM 长线驱动系统FSF-SPCC整体实现框图如图4 所示。

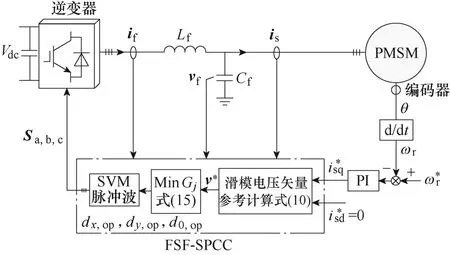
图4 PMSM 长线驱动系统FSF-SPCC 原理框图Fig.4 Block diagram for FSF-SPCC of a PMSM long-cable drive system

4 实验验证与分析

为验证本文所提FSF-SPCC 策略的有效性，搭建了实验样机，包含两电平三相逆变器、PMSM、LC 滤波器和磁滞制动器负载，实验平台如图5 所示，相应的参数见表 3。其中，控制器采用 DSP TMS320F28335，所提 FSF-SPCC 采样频率为fs=10 kHz，开关频率为fsw=5 kHz；传统单矢量MPC采样频率为fs=20 kHz，旨在于获得与所提方法相近的平均开关频率[20]。本文滑模增益λ的选择采用经验+试凑的方法，结合文献[17]可知：过小的λ将导致系统收敛速度慢容易不稳定；适当增大λ能够提高系统性能，但过大的λ将使所提价值函数式（8）退化为传统价值函数式（5）而降低系统性能，故需折衷考虑。通过从小到大单方向增大λ进行试凑，最终选择λ=104以获得较为满意的控制性能。

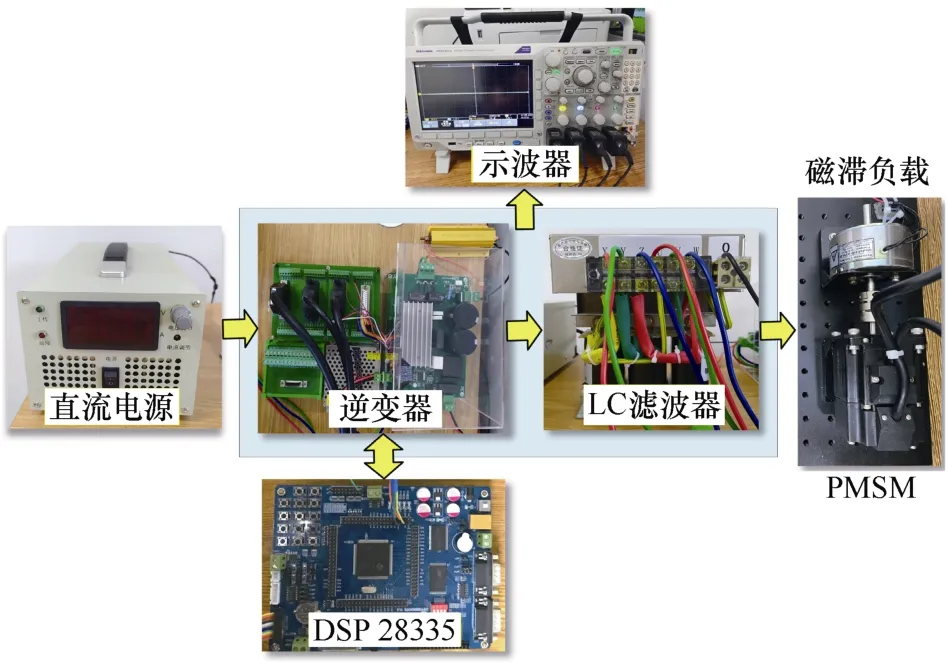
图5 实验平台Fig.5 Experimental platform

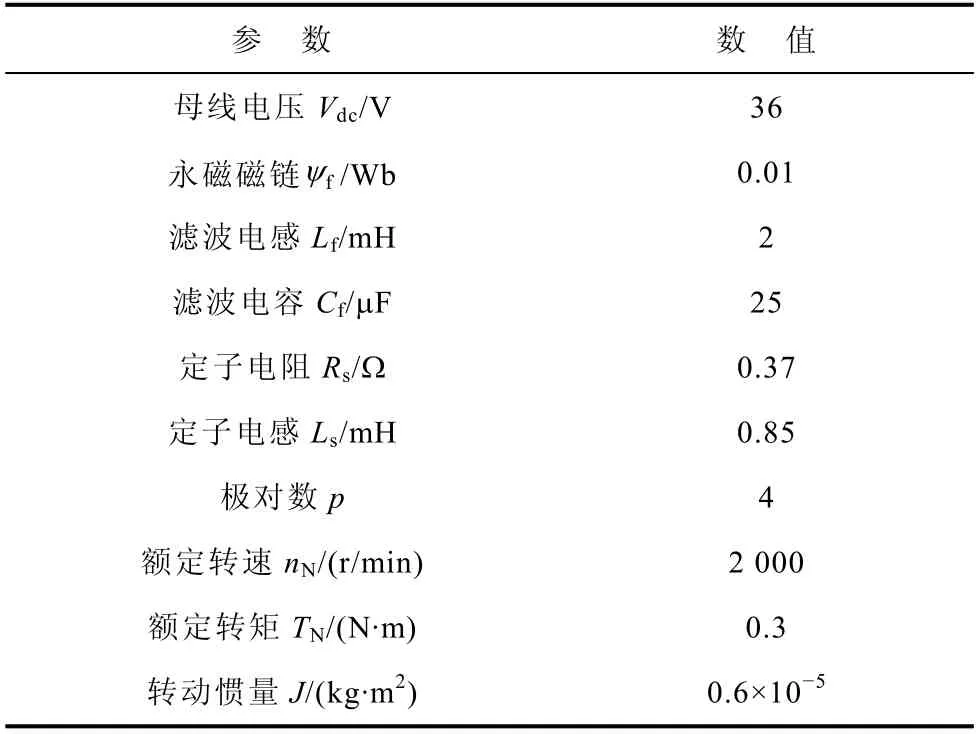
表3 PMSM 长线驱动系统参数Tab.3 Parameters of a PMSM long-cable drive system

4.1 稳态性能评估

图6 分别为采用传统单矢量MPC 和所提FSFSPCC 下，系统运行在1 000 r/min 时的稳态实验波形。图中，n为转速、isq为q 轴定子电流、vfa和isa分别为a 相滤波电容电压和定子电流。从图6 可看出，传统单矢量MPC 因一个Ts内仅作用一个电压矢量且未考虑输出LC 滤波器特性，使得vfa和isa产生了较大稳态纹波和畸变。相反地，所提 FSFSPCC 策略将价值函数设计成滑模面跟踪的形式，固有地控制了两个状态变量is和vf，故有效抑制了谐振能量的激发，从而获得了较优定子电流稳态性能。此外，对比图6c 和图6d 中定子电流isa的谐波谱可知，与传统方法相比，采用所提FSF-SPCC 方法的定子电流总谐波畸变率（Total Harmonic Distortion,THD）下降了近5 倍。此外，传统单矢量MPC谐波谱分布范围较广，开关频率不固定，不利于输出LC 滤波器的设计。相比之下，所提FSF-SPCC的谐波谱集中在开关频率fsw及其整数倍处，故实现了恒定的开关频率。

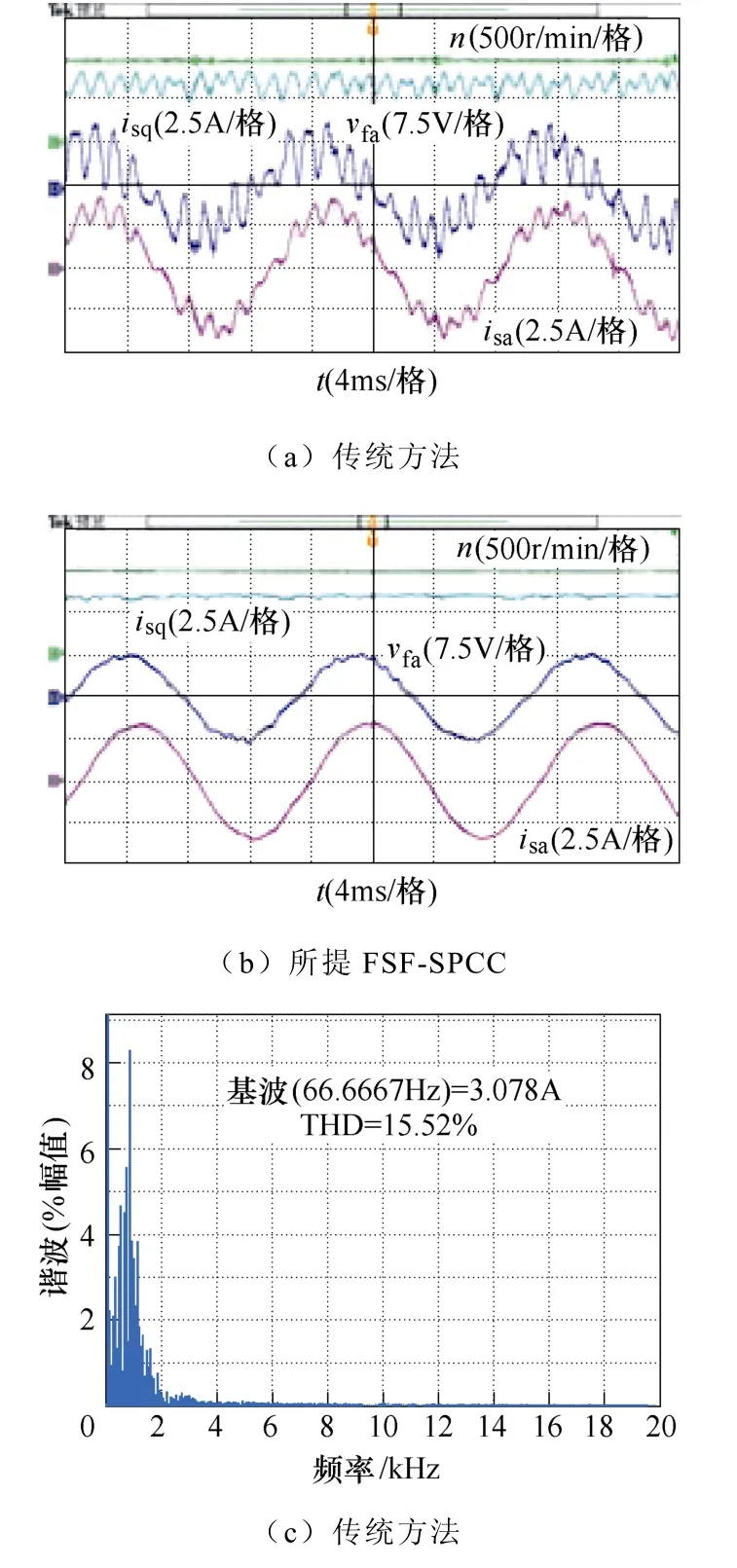
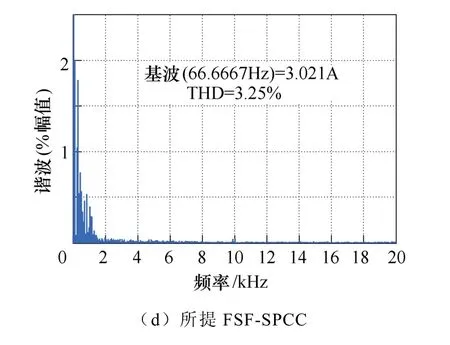
图6 系统稳态性能实验波形Fig.6 Experimental waveforms of system steady-state performance

4.2 动态性能评估

图7 分别为采用传统单矢量MPC 和所提FSFSPCC下，电机转速由500 r/min 阶跃上升至1 000 r/min时的动态性能实验结果。从图7 中可看出，传统单矢量MPC 和所提FSF-SPCC 可获得相似的调速和定子电流动态响应。尽管如此，所提FSF-SPCC 策略的稳态性能更优。

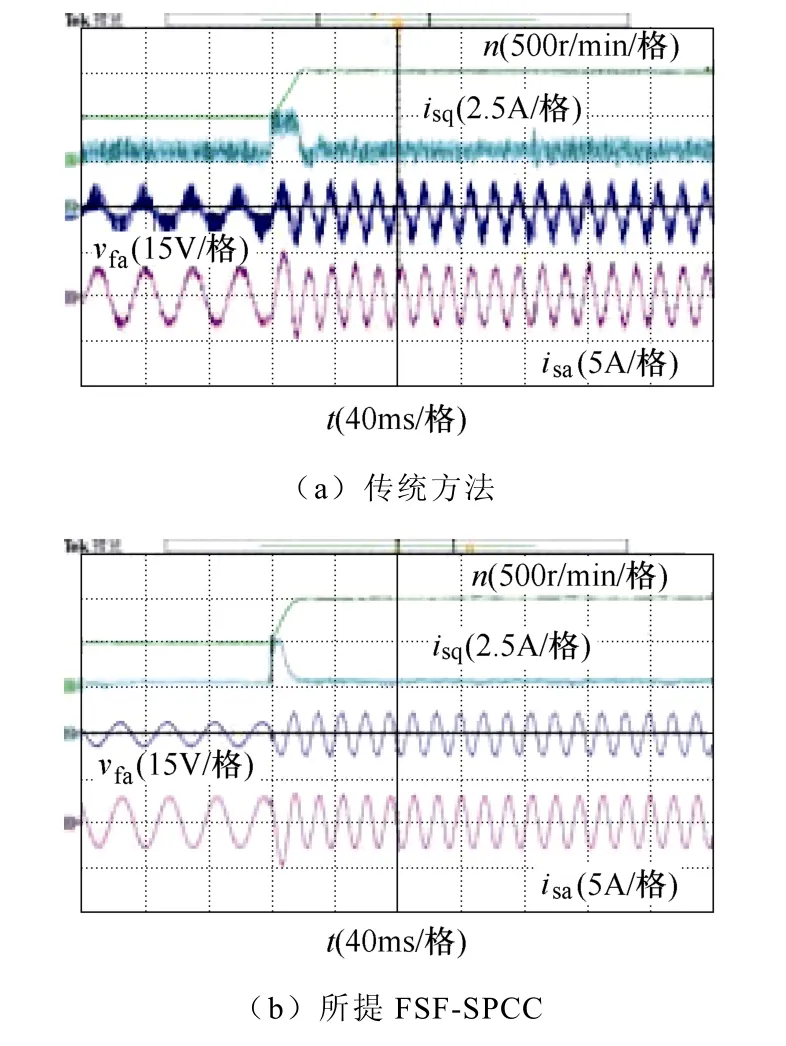
图7 系统调速动态性能实验波形Fig.7 Experimental waveforms of system speed regulation dynamic performance

4.3 定子电感参数失配下鲁棒性评估

图8 分别为采用传统单矢量MPC 和所提FSFSPCC 在1 000 r/min 下，定子电感Ls产生±50 %失配时的系统鲁棒性实验结果。从图8a 和图8b 可以看出，当控制器中定子电感参数Ls减小50 %时，两种控制方法下的系统性能均无显著变化，亦没有出现谐振现象。故传统单矢量 MPC 和所提 FSFSPCC 对定子电感Ls减小时的失配均具有较强鲁棒性。类似地，图8c 和图8d 分别为采用传统单矢量MPC 和所提FSF-SPCC 在1 000 r/min 下，定子电感Ls产生+50 %失配时的鲁棒性实验结果。可以看出，当Ls增加50 %时，传统单矢量MPC 下的定子电流激起了谐振现象，导致系统稳态畸变和稳定性变差。相反地，所提FSF-SPCC 策略仍然能够保持较优控制性能，且无谐振发生。综上所述，所提FSF-SPCC 策略相较于传统单矢量MPC 在Ls参数失配下具有更强的鲁棒性。

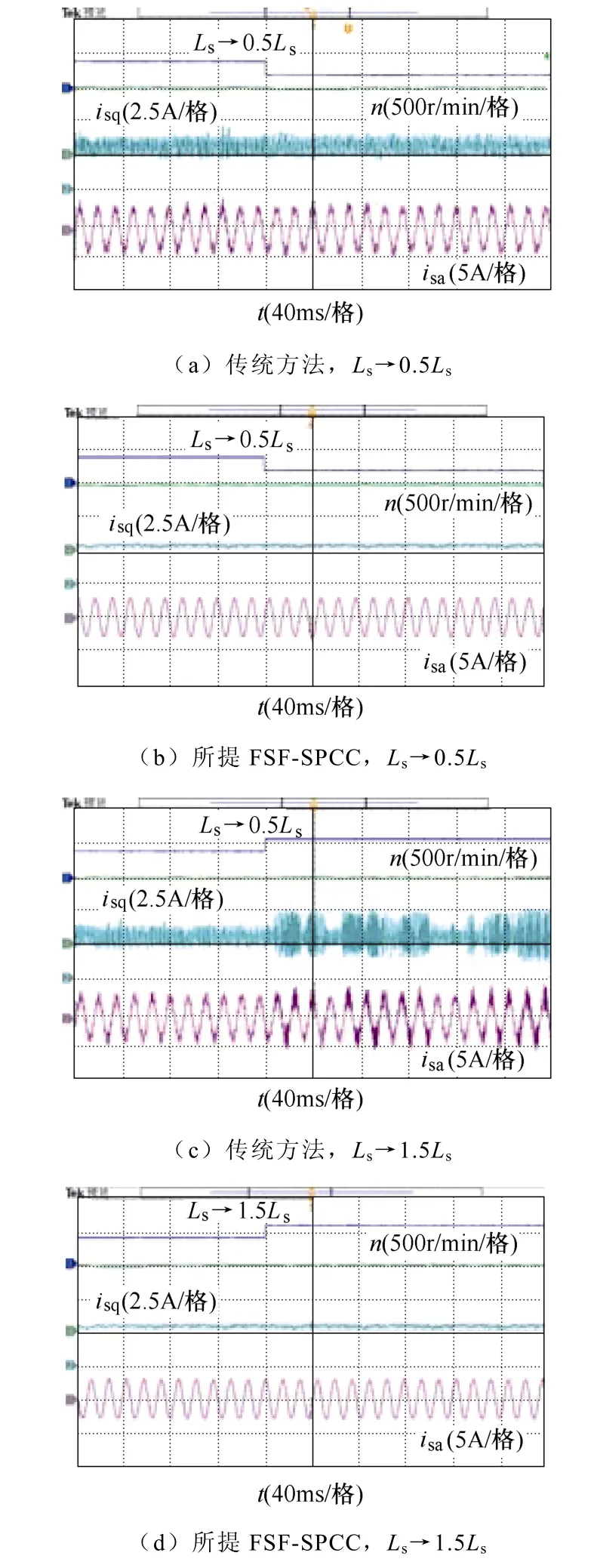
图8 定子电感Ls 增大50 %时实验波形Fig.8 Experimental waveforms with 50 % increase of stator inductance Ls

为了获得能够保持系统稳定的定子电感Ls的变化区间，考虑到本文所提方法最终是通过遍历6 个扇区以评估价值函数式（15），最终可选择出能够最小化式（15）的最优扇区及其对应的最优电压矢量组合和占空比。因该过程是非线性不连续的，故无法简单利用线性系统理论去分析能保持系统稳定的电感变化区间。这里，通过对电感参数进行扫描分析仿真，绘制出了定子电感Ls从0.1～4 倍（间隔0.1）范围变化时的 a 相定子电流总谐波畸变率isa_THD，如图9 所示。从图9 中可看出，当定子电感参数减小到0.2Ls以下（即降低80 %以上）或增大到3.7Ls以上（即增加270 %以上）时，定子电流THD 将超过100 %，此时系统已经发生谐振失稳。换句话说，本文所提方法能够保持系统稳定的定子电感区间为[0.2Ls,3.7Ls]。

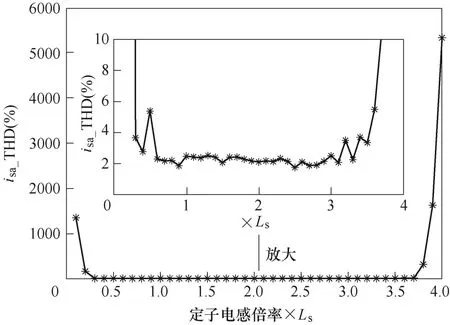
图9 Ls 从0.1～4 倍变化时a 相定子电流THDFig.9 Stator-current THD when Ls changes from 0.1 to 4 times

此外，本文所提方法的不足在于：一方面，因算法实现的遍历过程非线性不连续，故无法利用线性理论严格分析系统稳定性；另一方面，本方法滑模切换增益/权重因子的调节主要依据定性理论和经验试凑指导，缺少严格的解析理论分析。以上均将成为未来要开展的重要工作。

5 结论

针对带输出LC 滤波器的PMSM 长线变频驱动系统，首先基于滑模切换函数设计了离散预测模型，并构建了一种基于滑模面跟踪的新型价值函数，其固有地实现了系统多变量控制并有效抑制了谐振。其次，基于滑模参考电压矢量跟踪提出了一种三矢量定频FSF-SPCC 策略。所提控制方法实现了恒定开关频率，方便了输出LC 滤波器的设计。实验结果表明，所提FSF-SPCC 可有效提升系统的稳态性能和鲁棒性。